计及锁相环的光伏并网系统间谐波发射特性

钟庆，罗擎天，王钢，汪隆君

（华南理工大学电力学院，广州 510640）

0 引言

随着光伏并网系统的容量不断增加，其产生的间谐波问题引起广泛关注[1-3]。光伏并网系统产生的间谐波可能会导致网络中谐振频率的谐波放大、保护意外动作、灯具闪变值超标等问题[4-6]。尤其是次同步频段的间谐波较为显著时，可能与邻近发电机轴系机械振荡相互作用，诱发次同步振荡问题[7]。因此，建立光伏并网系统的间谐波分析模型，分析光伏并网系统的间谐波发射特性对解决光伏并网系统带来的间谐波问题具有重要意义。

电力系统中存在大量变频调速器类和带波动性负载的感应电动机等间谐波源，正常运行时会向电网注入大量间谐波电流[8-9]，在系统产生电压波形畸变，光伏并网点处的电压背景间谐波会导致其向电网注入间谐波电流[2-3]，而锁相环会影响光伏并网系统在电压背景间谐波下的间谐波发射特性[10]。

文献[10]所建立的小信号阻抗模型可用于计算电压背景间谐波作用下光伏并网系统发射的同频同序间谐波电流，但没有考虑频率耦合，并且没有计及电压外环。文献[11-13]考虑了频率耦合，但同样没有计及电压外环。上述文献讨论了换流器在电压背景间谐波作用下的谐波阻抗，但没有对换流器的间谐波发射特性以及控制系统中各频率分量的耦合进行分析。而且小信号模型只能反映某一稳态运行点附近换流器的“线性化”特性，当扰动过大或者变化剧烈时，小信号模型偏差可能较大，而动态相量法[14]能够用于动态过程的谐波分析[15]、谐波传递规律分析[16-17]以及电磁暂态建模仿真与分析[18-20]。文献[18-19]建立了逆变型分布式微电网动态相量模型，但仅考虑了dq轴电流内环的直流分量，并且认为锁相环输出是理想的，文献[20]则未对锁相环进行讨论。

为此，本文首先利用dq 变换和动态相量的定义，推导得到了dq 轴坐标系下动态相量与序分量动态相量的转换关系，以此作为后续分析的数学基础。然后以单同步坐标系锁相环为研究对象，基于该转换关系，将锁相环的时域模型转换为序分量动态相量模型。通过改变锁相环模型中的输入变量，分析了交流系统电压背景间谐波对锁相环输出的影响。然后将光伏并网系统拆分为5 个模块，分析了锁相环输出的各频率分量对三相交流电压、电流dq 变换模块和d、q轴调制信号逆变换模块中控制变量各频率分量的影响。最后搭建仿真模型，对比了锁相环理想输出和计及锁相环动态情况下，各模块输出变量的差异，验证了本文理论分析结果的正确性。

1 dq 轴坐标系下动态相量与序分量动态相量的转换关系

三相静止坐标系变换到dq 轴坐标系的变换公式为

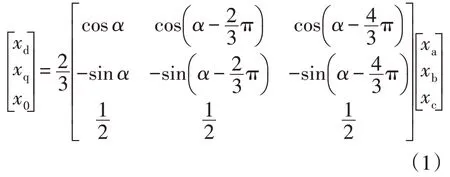
式中：α=ωst+θ；xd、xq、x0为dq 坐标系下的d、q、0轴时域量；xa、xb、xc为三相静止坐标系下的三相时域量；ωs为工频对应的角频率；θ为d轴与a轴的夹角。

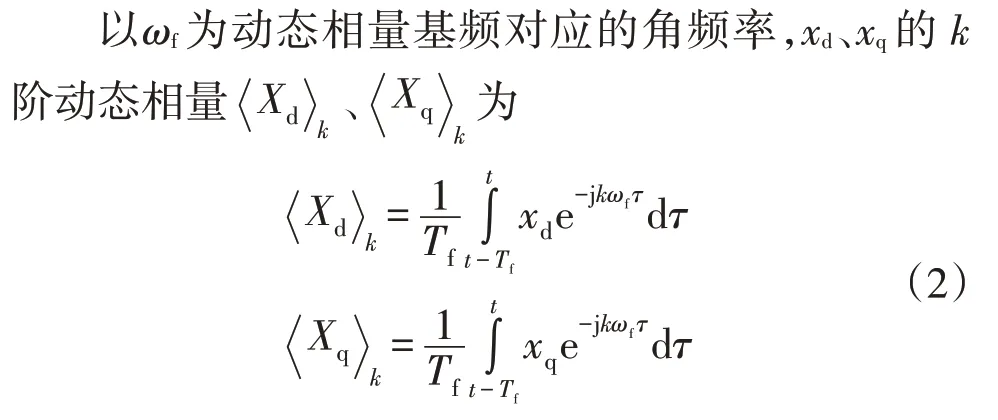
式中，Tf=2π/ωf。根据序分量动态相量的定义[22]，可得序分量动态相量转换到dq 轴坐标系下动态相量的变换关系为

同理，可推导得到dq 轴坐标系下动态相量转换到序分量动态相量的变换关系为

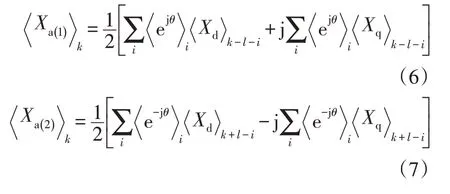
2 锁相环的序分量动态相量模型

本文研究对象为单同步坐标系锁相环，其控制框图见图1。

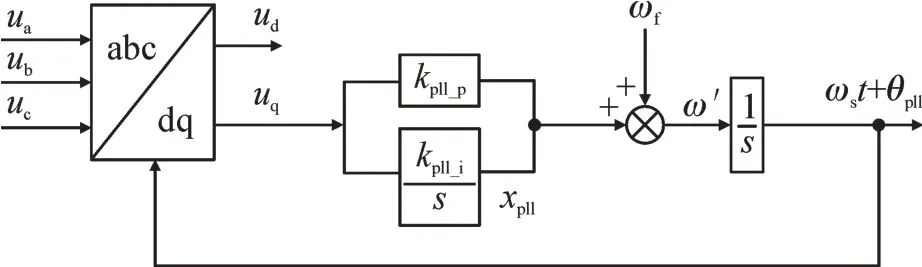
图1 单同步坐标系锁相环控制框图Fig.1 Control diagram of SSRF-PLL

图中，ua、ub、uc为并网点处三相电压；ud、uq分别为并网点电压锁相环d、q轴分量；ω′为锁相环输出角频率；kpll_p、kpll_i为锁相环PI 环节的PI 参数；xpll为锁相环PI 环节的积分输出。

由图1 可得锁相环的时域数学模型为

将式（8）转换为动态相量模型，利用dq 轴坐标系下动态相量与序分量动态相量的转换关系，可得锁相环k阶序分量动态相量模型为

3 间谐波发射特性分析

以图2 所示的单级式光伏并网系统为研究对象。

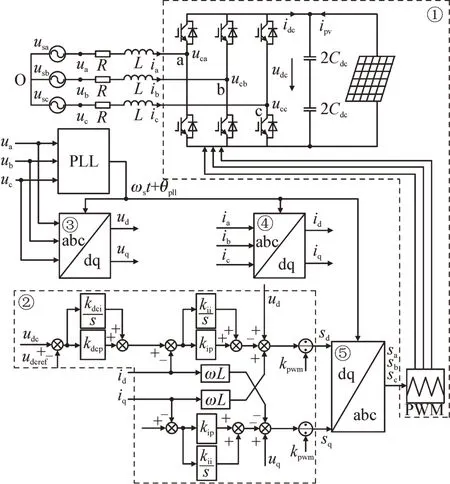
图2 单级式光伏并网系统Fig.2 Single stage grid-connected PV system

图中，O 点为交流电网中性点；usa、usb、usc为交流系统电压；uca、ucb、ucc为逆变器交流侧输出电压；ia、ib、ic为逆变器交流侧电流；udc为直流侧电压；idc为直流侧电流；ipv为光伏电池输出电流；R、L为交流滤波器的等效电阻和电感；Cdc为直流侧总电容值；id、iq分别为交流侧电流d、q轴分量；udcref为直流电压指令值；kdcp、kdci及kip、kii分别为电压外环及电流内环PI调节器的比例系数和积分系数；kpwm为PWM 等效增益；sd、sq分别为调制信号的d、q轴分量；sa、sb、sc分别为三相调制信号。

为了分析锁相环对光伏并网系统间谐波发射特性的影响，本文将系统分成5 个模块：模块1 为一次回路；模块2 为控制系统中由d、q轴电压、电流分量经电压、电流前馈控制生成d、q轴调制信号部分；模块3 和模块4 分别为控制系统中三相电压、电流abc-dq 变换生成d、q轴电压、电流信号部分；模块5 为控制系统中d、q轴调制信号dq-abc 变换生成三相调制信号部分。

3.1 模块1与模块2

模块1 和模块2 不同频率的输入、输出信号之间的关系可由文献[21]获得。并且由文献[21]可知，当三相调制信号存在任意一个角频率为ωs±nmωf（n为任意自然数）的间谐波分量时，将在光伏逆变器交流侧电流中产生角频率为ωs±mωf、ωs±2mωf、…的系列间谐波分量。

因为模块2 为线性系统，因此d、q轴调制信号为输出，与d、q轴电压、电流信号分量为输入同频。

3.2 模块3

模块3 的输入为三相交流系统电压，输出为d、q轴电压分量。假定锁相环为理想输出，即θpll=0，即除外，其余各项均为0。根据序分量动态相量转换到dq 轴坐标系下动态相量的变换关系可知，工频正序电压仅作用于d、q轴电压直流分量，其表达式为

同理可知，ωs+mωf的间谐波电压正序分量仅作用于ud和uq的mωf间谐波分量，其表达式为

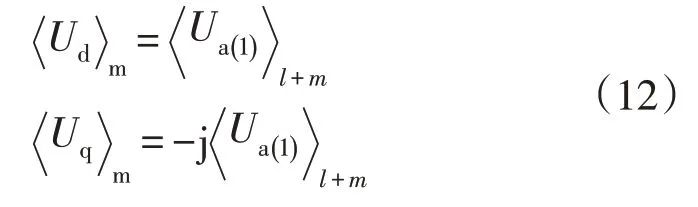
由第2 节分析可知，当交流系统电压存在ωs+mωf的背景间谐波时，计及锁相环动态，其实际输出包含mωf、2mωf、…系列间谐波分量，即根据序分量动态相量转换到dq 轴坐标系下动态相量的变换关系，可得ud和uq的nm阶动态相量的表达式为

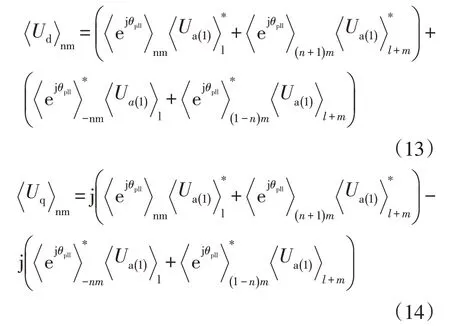
因此，工频正序电压和ωs+mωf间谐波电压正序分量与d、q轴电压分量的关系见图3。工频正序电压不仅作用于d、q轴电压直流分量，还将通过作用于ud和uq的nmωf分量。ωs+mωf的间谐波电压正序分量不仅作用于ud和uq的mωf分量，还将通过作用于ud和uq的nmωf分量。

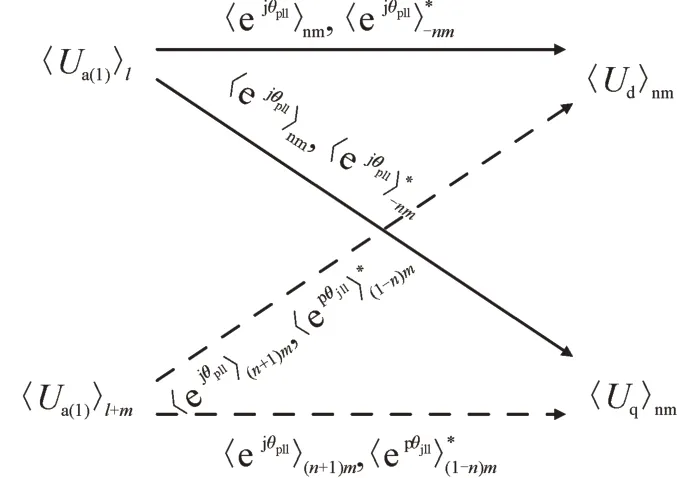
图3 工频正序电压和ωs+mωf间谐波电压正序分量与d、q轴电压间谐波分量的关系Fig.3 Relationship between the positive sequence component of power frequency positive sequence voltage and harmonic voltage ωs+mωf and harmonic component of voltage in dq coordinate

3.3 模块4

模块4 的输入为三相交流电流，输出为电流的d、q轴分量。假定锁相环为理想输出，根据序分量动态相量转换到dq 轴坐标系下动态相量的变换关系可知，工频正序电流仅作用于d、q轴电流直流分量，其表达式为

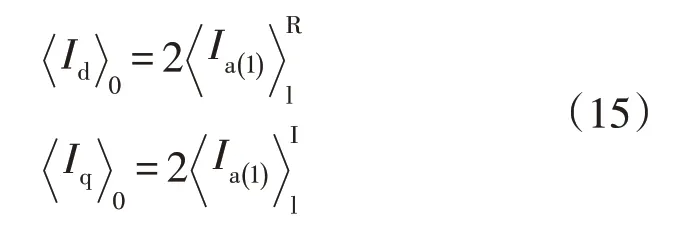
同理可知，ωs±mωf的间谐波电流正序分量仅作用于id和iq的mωf间谐波分量，其表达式为

以此类推，ωs±nmωf的电流正序分量仅作用于id和iq的nmωf分量。

计及锁相环动态时，id和iq的rm阶（r为自然数）动态相量表达式为

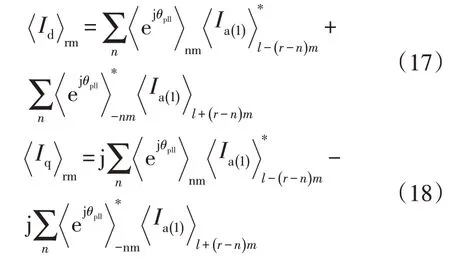
因此，三相交流电流与d、q轴电流分量的关系见图4。工频正序电流不仅作用于d、q轴直流分量，还将通过作用于id和iq的nmωf分量；ωs±mωf的间谐波电流正序分量不仅作用于id和iq的mωf间谐波分量，还将通过和作用于id和iq的（n1）mωf分量。

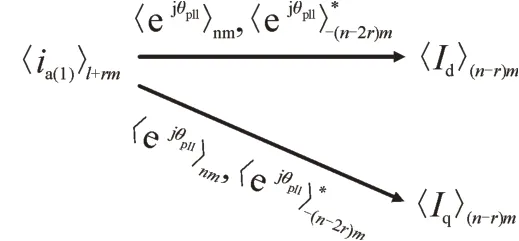
图4 三相交流电流与d、q轴电流间谐波分量的关系Fig.4 Relationship betweenthree phase AC current and inter-harmonic component of current in d、q coordinate

3.4 模块5

模块5 的输入为d、q轴调制信号，输出为三相调制信号。假定锁相环为理想输出，根据dq 轴坐标系下动态相量转换到序分量动态相量的变换关系可知d、q轴调制信号的直流分量仅作用于三相调制信号的工频正序分量，其表达式为

同理可知，d、q轴调制信号mωf的间谐波分量仅作用于三相调制信号的ωs±mωf的间谐波正序分量，其表达式为

以此类推，ωs±nmωf的电压正序分量仅作用于ud和uq的nmωf分量。

计及锁相环动态时，三相调制信号的l+rm和l－rm阶正序序分量动态相量为

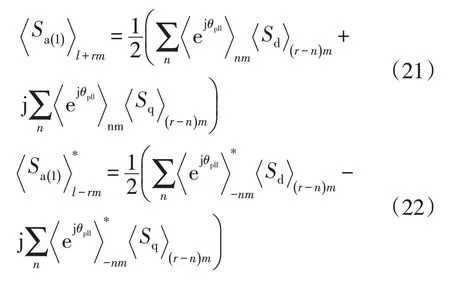
因此，d、q轴调制信号与三相调制信号的关系见图5。d、q轴调制信号的直流分量不仅作用于三相调制信号的工频正序分量，还将通过作用于三相调制信号的ωs+nmωf间谐波分量；d、q轴调制信号mωf的间谐波分量不仅作用于三相调制信号的ωs±mωf的间谐波正序分量，还将通过和作用于三相调制信号的ωs+（n±1）mωf间谐波分量。

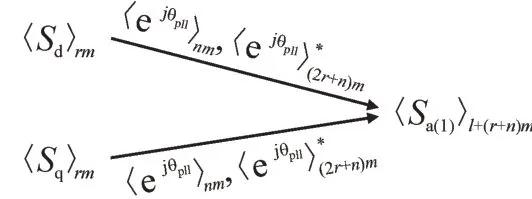
图5 d、q轴调制信号与三相调制信号的关系Fig.5 Relationship between modulation signal and corresponding components in dq coordinate

3.5 小结

通过各模块的分析可知：由于并网点处三相电压存在ωs+mωf的背景间谐波正序分量，计及锁相环动态后，锁相环的实际输出包含mωf、2mωf、…系列间谐波分量，将影响三相交流电压、电流变换到d、q轴电压、电流分量和d、q轴调制信号变换到三相调制信号的变换过程，并且在变换过程中各间谐波分量间产生了耦合作用[22]。相比于锁相环为理想输出的情况，计及锁相环不会让光伏并网系统发射的间谐波电流频率改变[23]，但是会因为锁相环输出各频率分量的存在而影响光伏并网系统发射的间谐波电流幅值。

4 仿真验证

本文搭建了如图2 所示的光伏并网系统仿真模型，系统参数见表1，光伏电池参数见表2。

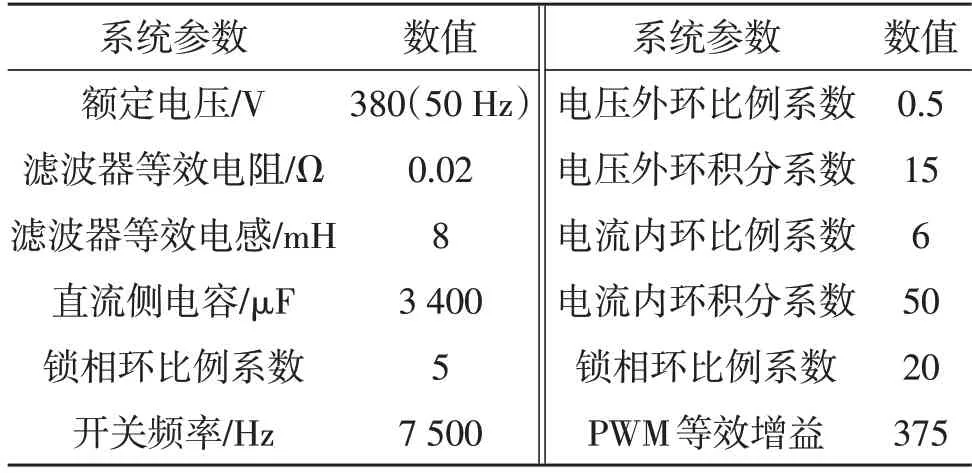
表1 系统参数Table 1 Parameter of system

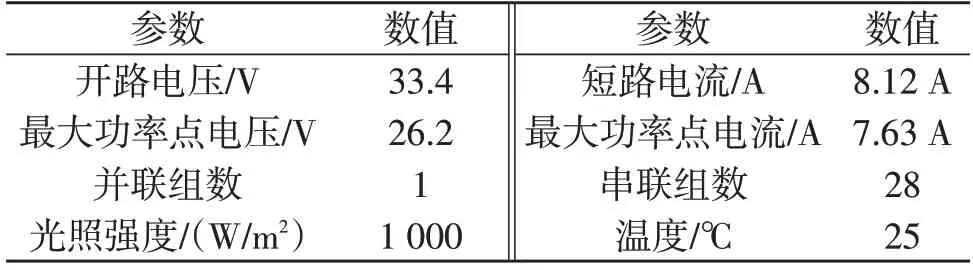
表2 光伏电池参数Table 2 Parameter of PV

给定交流系统电压存在与工频正序电压同相的频率为45 Hz，幅值为10%额定电压的背景间谐波。由第2 节分析可知，计及锁相环动态时，锁相环输出的θpll应含有频率为5、10、15 Hz、…的系列间谐波分量。

对仿真中锁相环输出的θpll进行频谱分析，结果见图6，仿真结果与理论分析结果一致，从而可验证本文锁相环模型的正确性。随着频率的升高，θpll的间谐波分量幅值也随之减小。

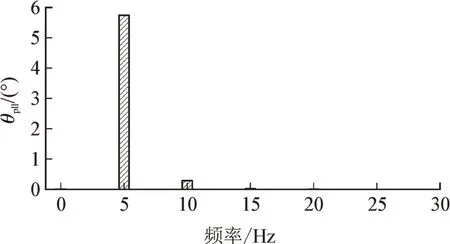
图6 锁相环输出的θpll 频谱图Fig.6 Spectrum of θpll of PLL output

为分析θpll系列间谐波分量对后续变换影响，对比计及锁相环动态和锁相环理想输出的光伏并网系统d、q轴电压分量和电流分量的频谱分析结果见图7。

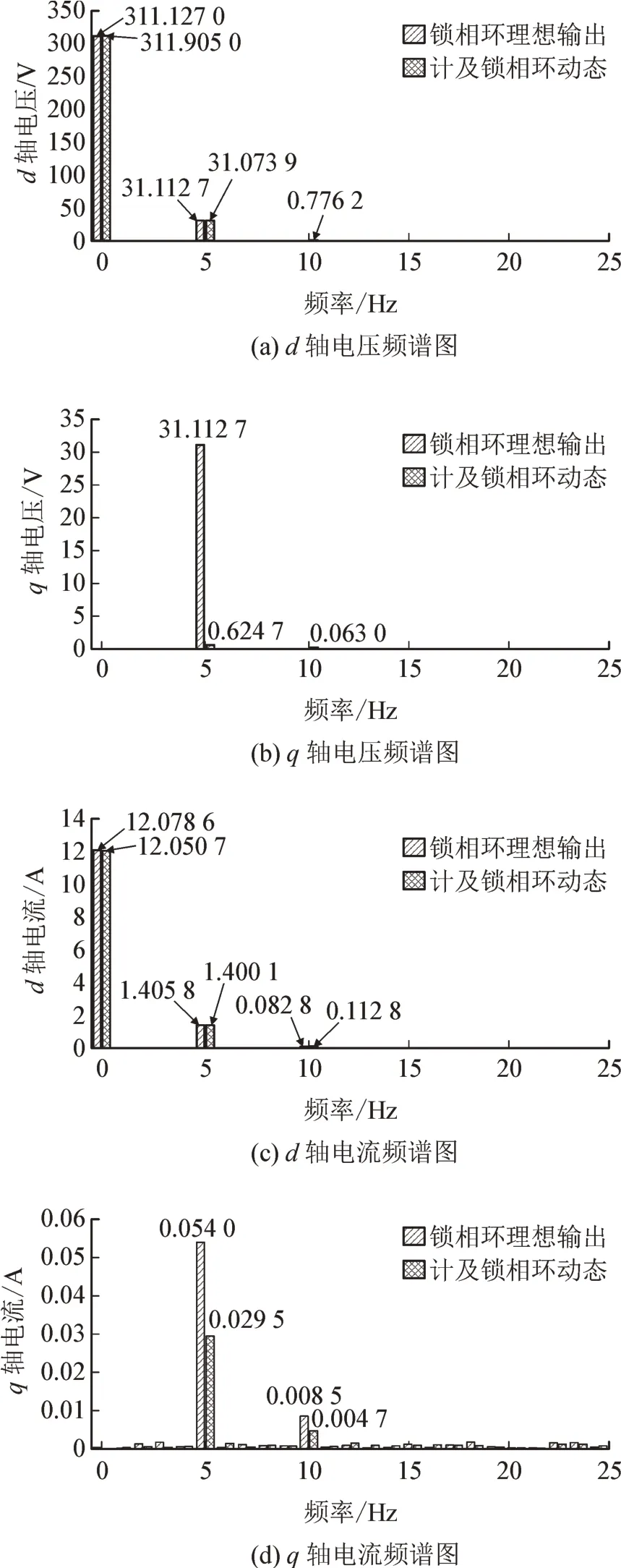
图7 d、q轴电压、电流的频谱图Fig.7 Spectrum of voltage and current in d、q coordinate

计及锁相环动态后，d轴电压直流分量和5 Hz分量变化不大，但受θpll的影响出现了10 Hz 分量，其幅值为0.776 2 V。q轴电压5 Hz 分量受θpll的影响，由31.112 7 V 减小为0.624 7 V，同时出现了10 Hz分量，其幅值为0.063 0 V。d轴电流各频率分量的变化不大，但q轴电流5 Hz 和10 Hz 分量由0.054 0 A和0.008 5 A 减小为0.029 5 A 和0.004 7 A。

d、q轴调制信号频谱对比结果分别见图8（a）和图8（b）。

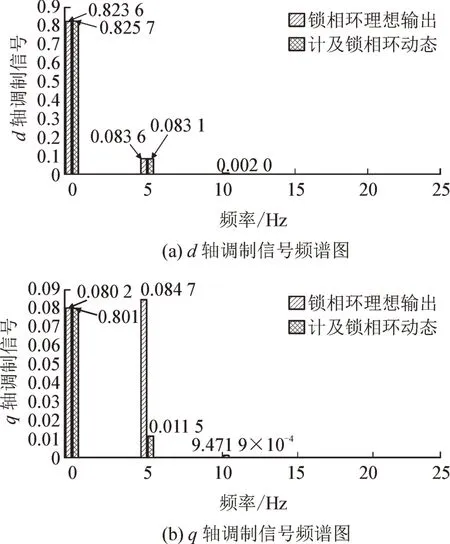
图8 d、q轴调制信号Fig.8 Spectrum of modulation signal in d、q coordinate

计及锁相环动态后，d轴调制信号直流分量和5 Hz 分量变化不大，但受θpll的影响出现了10 Hz 分量，幅值为0.002 0。q轴调制信号中5 Hz 分量受θpll的影响，幅值由0.084 7 减小为0.011 5，同时出现了10 Hz 分量，幅值为9.471 9×10-4。

a 相调制信号的频谱对比结果见图9。45 Hz 分量幅值变化不大，但相位从86.981 6°变为89.372 0°。55 Hz 分量幅值从0.004 5 变为0.008 7，相位从-4.282 2°变为-5.085 2°。

图9 a相调制信号的频谱图Fig.9 Spectrumof modulation signal of phase A

a 相交流电流频谱对比结果见图10。计及锁相环动态后，光伏并网系统不会出现新的间谐波电流分量。

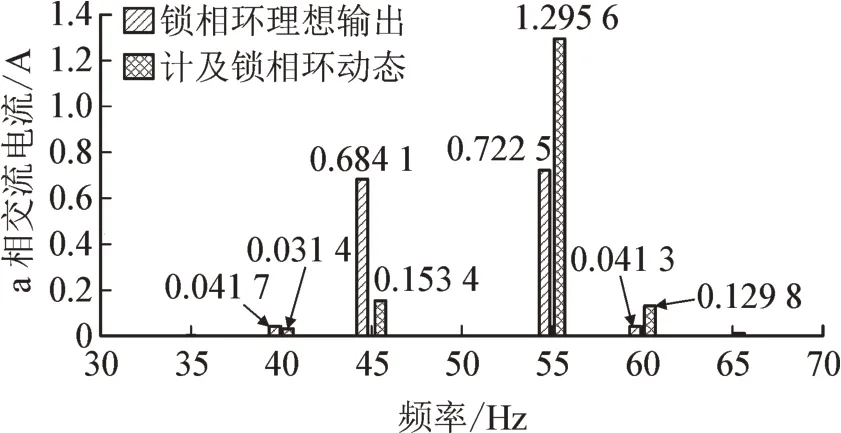
图10 a相交流电流的频谱图Fig.10 Spectrum of AC current of phase A

但θpll系列间谐波分量的存在会影响光伏并网系统发射的间谐波电流幅值，其中40 Hz 分量由0.041 7 A 减小为0.031 4 A；45 Hz 分量由0.684 1 A减小为0.153 4 A；55 Hz 分量由0.722 5 A 增加为1.295 6 A；60 Hz 分量由0.041 3 A 增加为0.129 8 A。从而验证了本文理论分析的正确性。

5 结语

本文利用d、q轴动态相量与序分量动态相量的转换关系建立了锁相环的序分量动态相量模型，分析了电压背景间谐波下锁相环的输出响应及其对控制系统各模块的影响，从而获得了计及锁相环后的光伏并网系统间谐波发射特性。背景间谐波下锁相环的输出会产生一系列的频率分量，但这些分量不会影响光伏并网系统的间谐波电流频率，只会影响其幅值。