双轮半转叶轮水轮机获能特性分析

2022-11-03孙承坤王孝义张旭成徐向荣

安徽工业大学学报（自然科学版） 2022年4期

孙承坤，王孝义，陈航，张旭成，邱晗，徐向荣

(安徽工业大学机械工程学院，安徽马鞍山 243032)

潮流能是一种储量高、能量密度大的清洁可再生能源，具备良好的开发前景[1-2]。潮流能的开发是以水轮机为核心部件，其中垂直轴水轮机因结构简单、便于维护的特点而受到广泛关注[3-5]。随着水轮机发电技术的成熟与发电需求量的增大，多轮型水轮机逐渐成为新的研究方向。Goude等[6]采用二维涡方法研究不同布置方式下水轮机组效率的变化规律，发现以之字型布置方式的水轮机组的获能效率较高；Sun 等[7]数值模拟发现，Savonius 叶轮之间的相互作用效果与叶轮的相对旋转方向、间距等因素有关；王凯等[8]发现，不同相位角下的双轮水轮机获能效率差异明显，相位角为0°时获能效率最低；Li等[9-10]探究了不同布局参数下双轮水轮机的水动力性能，发现双轮水轮机效率高于单轮水轮机；Fertahi等[11]通过叶轮之间的嵌套改善水轮机的获能特性；王凯等[12]设计同轴双Darrieus转子水轮机，数值模拟结果表明，双Darrieus转子水轮机输出波动幅值较单Darrieus水泥机低；孙殿凯[13]发现，双轮水轮机输出能力同时受轴距与相对位置角的影响。上述研究表明，多轮水轮机中叶轮的协同运作可有效提高水轮机的输出能力，布局方式极大影响其作用效果。

半转叶轮作为一种新型升阻复合型叶轮[14]，由于不对称运动特点，使得流体在流经叶轮两侧产生不同的绕流运动，并在叶尖处产生流体加速作用。本课题组[15]将该效果用于改善水轮机的获能特性，提出了双轮半转叶轮水轮机。在此基础上，以双轮半转叶轮水轮机为研究对象，数值模拟分析旋向与布局参数对其获能特性的影响，获得双轮半转叶轮水轮机的近优布局参数，以期为后续双轮半转叶轮水轮机的工程应用提供方法与技术支撑。

1 半转叶轮数值模拟

1.1 半转叶轮工作原理

半转叶轮源于半转机构，半转机构是一种能够实现不对称运动的新型机构，如图1。其中定轮为固定件，定轮与动轮的传动比为2，当系杆带动动轮以角速度ω围绕定轮中心转动时，半转构件将以角速度ω/2 围绕动轮中心转动，实现半转构件的不对称运动。将半转机构用于潮流能水轮机领域，系杆对称延伸为转臂，半转构件沿展向延长形成叶片并在转臂两端垂直布置，构成半转叶轮，其工作原理如图2。

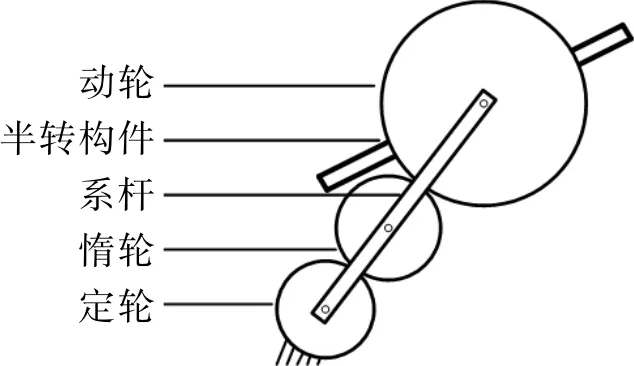
图1 半转机构Fig.1 Half-rotating mechanism

图2 半转叶轮工作原理Fig.2 Working principle of half-rotating impeller

半转叶轮在运动过程中，叶片在随转臂围绕点O公转的同时，会绕其与转臂铰接点自转。当来流沿Y轴负方向以速度U作用于半转叶轮时，以Y轴为中心线，划分叶轮两侧流域。当叶片的主运动方向与来流方向夹角为锐角时，叶片处于叶轮右侧流域，称为顺流区；当叶片的主运动方向与来流方向夹角为钝角时，叶片处于叶轮左侧流域，称为逆流区。叶片在两侧流域运动时，由于叶片攻角的不断改变，叶片同时受到沿来流方向的阻力FD与垂直于来流方向的侧向力FL。当来流作用于半转叶轮时，叶轮沿来流方向从顺流区朝逆流区转动。

1.2 数值模拟与有效性验证

采用XFlow 软件模拟分析水轮机获能特性。通过XFlow 自身建模功能实现叶片的建模，通过定义叶片的公转与自转实现其半转运动。对于湍流模型，选取壁面自适应局部涡黏性模型；对于入口边界条件，设定流体为水、温度为288.15 K、动力黏度系数0.001 Pa·s、流体密度998.3 kg/m3。设定解析度细化算法为自适应到壁面的细化算法，全局解析度为0.25 m，叶片附近的解析度为0.007 812 5 m。建立的计算域与边界条件如图3。

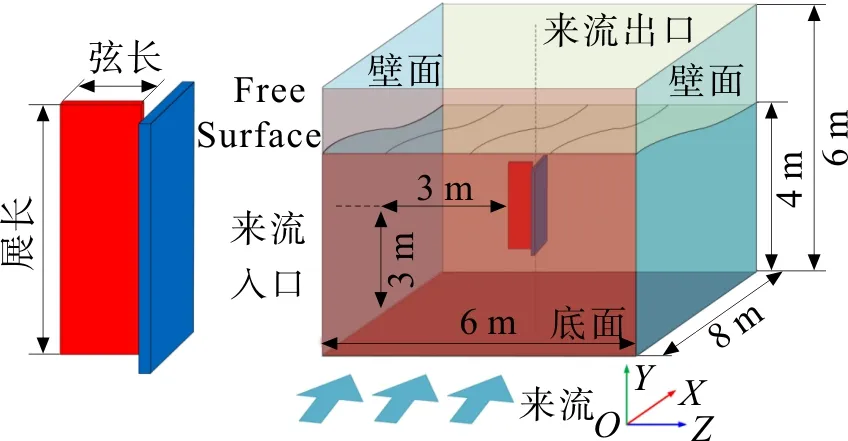
图3 计算域与边界条件Fig.3 Computation domain and boundary conditions

获能效率Cp是衡量水轮机获能特性的重要指标，为水轮机输出功率与来流输入功率的比值，如式(1)。

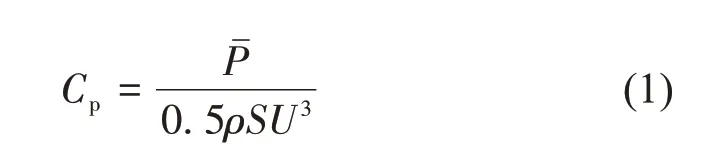
式中：Pˉ为双轮水轮机的输出功率；ρ为流体密度；S为水轮机扫掠面积；U为来流速度，文中取U=1 m/s。

为验证XFlow 数值模拟结果，将单轮半转叶轮水轮机数值模拟结果与课题组前期实验结果[16]进行对比，结果如图4。叶轮尺寸见表1，其中转臂半径为叶片中心转动半径，输出转矩为一个运动周期内叶轮输出转矩的平均值。从图4 可知：数值模拟结果与实验结果变化趋势相近，且最高获能效率贴合良好，证明采用XFlow 模拟计算出的水轮机获能效率数值具备可信性；数值模拟下单轮半转叶轮水轮机效率可达46.6%。

图4 单轮半转叶轮水轮机数值模拟与实验结果Fig.4 Simulation and experimental results comparison of HRITT

表1 半转叶轮结构尺寸Tab.1 Structure size of half-rotating impeller

2 模拟结果与分析

为便于表征双轮半转叶轮水轮机的获能特性，体现双轮与单轮半转叶轮水轮机获能特性的差异，定义双轮半转叶轮水轮机能效指数η，如式(2)。

式中：Cpt为双轮半转叶轮水轮机的获能效率；Cps为单轮半转叶轮水轮机的最高获能效率。

采用能效指数衡量水轮机输出功率的同时引入扫掠面积比较，当且仅当η＞1 时，设计的双轮半转叶轮水轮机才会被认为优于单轮半转叶轮水轮机；当η＜1时，认为等迎流面积下，叶轮数的增加无法实现半转叶轮型水轮机获能的增大。文中叶轮结构参数如表1，在叶轮结构参数确定的基础上，通过式(2)计算能效指数Cps为46.6%。

2.1 旋向对能效指数的影响

鉴于半转叶轮转动方向的差异性，建立内外旋向下的双轮半转叶轮水轮机布置方案，如图5。双轮半转叶轮水轮机为单个水轮机机架中包含2个半转叶轮，两侧叶轮通过同一输出轴输出，故两侧叶轮呈镜像对称布置。其中轴距D为两侧叶轮旋转中心的距离。

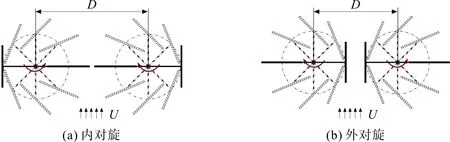
图5 内外对旋下的双轮半转叶轮水轮机布置方案Fig. 5 Layout scheme of THITT with internal and external rotation

由图5(a)可知，当D=2R+C时两侧叶轮完全贴合。考虑到叶片厚度会引起叶轮的干涉，故内外旋向下D=2R+1.05C，得到内外对旋下双轮半转叶轮水轮机能效指数随叶轮转速n变化趋势，如图6。由图6可知：双轮半转叶轮水轮机在不同旋向时水轮机的输出不同，内对旋下为正向增益，外对旋下为负向增益；内外对旋下能效指数差距较大，内对旋下最佳能效指数为1.067，外对旋下最佳能效指数为0.722。由此认为，外对旋下叶轮数的增加无法实现双轮半转叶轮水轮机总体输出的提高，故后文针对内对旋下的双轮半转叶轮水轮机进行讨论。

图6 能效指数随转速变化的规律Fig.6 Law of η changing with rotational speed

2.2 布局参数对能效指数的影响

双轮半转叶轮水轮机布局参数包括轴距D与初始安装角α。D为两侧叶轮转动中心的距离，如图7(a)。由图2可知，当叶轮两侧叶片分别与转臂呈垂直与平行关系时，来流方向与转臂垂直，定义安装关系为半转叶轮的初始相位。保持叶片与转臂位置关系不变，改变转臂位置，即可改变叶轮的初始安装角，其中沿来流方向转动为+α，如图7(b)，沿逆来流方向为-α，如图7(c)。

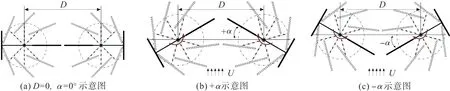
图7 双轮半转叶轮水轮机布局参数示意Fig.7 Schematic diagram of layout parameters of THITT

2.2.1 轴距对能效指数的影响

水轮机安装位置为初始位置，即α= 0°，取初始叶轮轴距D=2R+1.05C，模拟叶轮轴距D=2R+1.05C(0.38 m)，2R+1.10C(0.39 m)，2R+1.15C(0.40 m)，2R+1.20C(0.41 m)，2R+1.25C(0.42 m)，2R+1.30C(0.43 m)6 个运行工况，得到不同轴距下的最佳能效指数ηmax，如表2；同时计算不同轴距、不同叶轮转速下双轮半转叶轮水轮机的能效指数，结果如图8。

表2 不同轴距下双轮半转叶轮水轮机的最佳能效指数Tab.2 ηmax of THITT with different D

由图8 可见：不同轴距下双轮半转叶轮水轮机的η变化趋势相近，且均在转速n=1.2 r/s 时能效指数达至峰值；当D=2R+1.10C，n=1.2 r/s 时，能效指数最大，为1.224，相较于等迎流面积下的单轮半转叶轮水轮机，其获能特性提高了22.4%，此时轴距为当前计算方法中的最佳轴距，称为近优轴距；其他轴距时，ηmax＜1.224，且当D=2R+1.20C时，ηmax＜1。

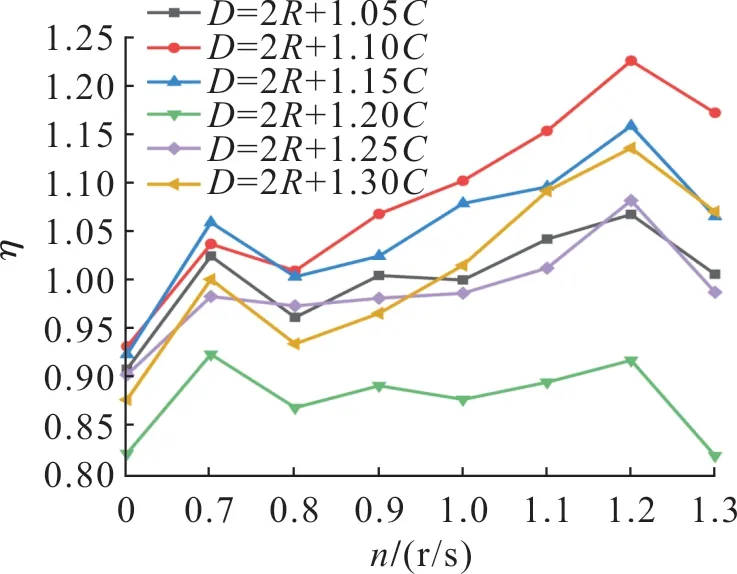
图8 不同轴矩和叶轮转速下双半转叶轮水轮机的能效指数(α = 0°)Fig.8 η of THITT with different D and n(α = 0°)

2.2.2 初始安装角对能效指数的影响

在得到近优轴距的前提下，即D=2R+1.1C，改变双轮半转叶轮水轮机的初始安装相位角α，计算α为-45°，-30°，-15°，0°，+15°，+30°，+45°时的能效指数，结果如图9。

由图9 可知，D=2R+1.1C时，不同初始安装相位角度下双轮半转叶轮水轮机的能效指数差异较大，等轴距下随α的增大η逐渐降低，当α= 0°时，能效指数最大，为1.224。这是由于初始安装角的改变使叶片在顺流区与来流方向的夹角变小，降低叶片受力，进而降低叶轮的输出。

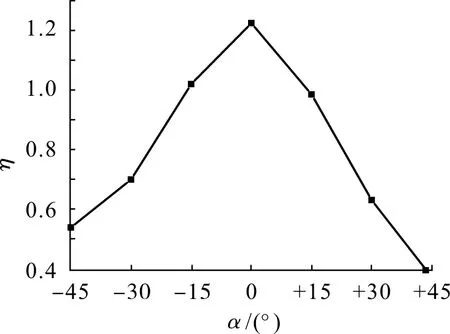
图9 能效指数随初始安装相位角变化的规律(D=2R+1.10C)Fig.9 Variation law of η with α(D = 2R + 1.10C)

2.2.3 布局参数对能效指数的综合影响

综上可知当D=2R+1.10C，α=0°时，双轮半转叶轮水轮机的能效指数最大。为避免两者存在耦合作用，计算不同轴距与初始安装角下的能效指数，结果如图10。由图10可知：等轴距下双轮半转叶轮水轮机能效指数变化差异较大，ηmax均随α的增大而逐步降低，而不同轴距下随α变化的趋势基本相同；当D=2R+1.10C，α= 0°时能效指数最大，为1.224，该布局参数为双轮半转叶轮水轮机近优布局参数；当双轮半转叶轮水轮机处于近优布局参数时，其获能特性相较于单轮半转叶轮水轮机提高了22.4%。

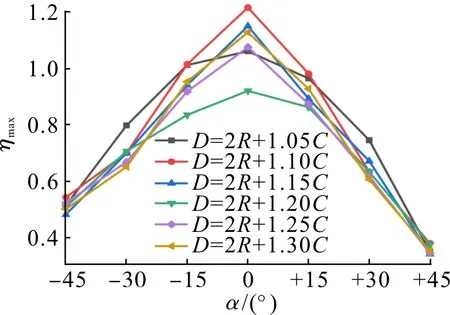
图10 不同布局参数下双轮半转叶轮水轮机最佳能效指数Fig.10 ηmax of THITT with different layout parameters

2.3 获能特性的增益机理

双轮半转叶轮水轮机获能特性高于单轮半转叶轮水轮机，获能特性的增益是通过两侧叶轮之间相互的扰流作用来实现的。为探讨其增益机理，对比分析近优布局参数(D=2R+1.10C，α=0°时)下双轮与单轮半转叶轮水轮机速度速度。由于叶轮转动的周期性，取转臂运动半个周期(1/2T)内的速度分布，如图11。由图11 可知：单轮半转叶轮水轮机在转动过程中，叶轮两侧存在明显的流动差异。初始位置时，水轮机受到来流作用开始转动；同时由于流体的流动连续性，流动空间的阻塞导致局部流速加快，流体主要在叶轮叶尖位置产生流体加速效果。对于单轮，流体加速效果在顺流区叶片的叶尖处，但流体加速效果主要消散于流域中。

图11 单双轮半转叶轮水轮机速度云图Fig.11 Velocity fields of HRITT and THITT

对于双轮半转叶轮水轮机，顺流区的合并使得前进叶片之间相互靠近，流体加速效果会相互作用在彼此的前进叶片中，加速区域实现了叠加，流体的加速效果得到增强。同时由于前进叶片之间的阻塞效果，流体加速效果还出现在单个叶轮中。而叶片处于顺流区时，叶片与来流攻角较大，叶片受力以阻力为主，来流速度的增大会导致叶片受力增大，利于水轮机做功。流场的差异主要体现为叶片受力改变，取初始位置处于顺流区叶片一个周期内所受阻力与侧向力在叶片运动切向上的分力，如图12，叶轮转速均为1.2 r/s。

由图12 可看出：双轮半转叶轮水轮机叶片受力变化趋势与单轮中叶片受力相同，这是由半转叶轮的做功方式决定的；但在相同位置下两者受力大小区别明显，这是双轮半转叶轮水轮机两侧叶轮相互作用导致的。对比叶片受力可发现：对于侧向力，当叶片处于逆流区，双轮叶片侧向力在切向上分力小幅降低；对于阻力，当叶片处于顺流区，双轮叶片阻力在切向上分力大幅增加，这与其速度云图中的差异是一致的。内对旋下双轮半转叶轮水轮机获能效率的增加主要通过对来流的诱导加速实现叶片受力增大，其作用域集中在叶轮的顺流区，叶片运动切向受力越大，能效指数越高。