平行板电容器串并联教学中问题分析

任 杰

（常熟理工学院电子信息学院，江苏苏州 215500）

电容器是除电阻之外的第二大常用的元件.通常情况下电容器是由两块金属电极之间夹一层绝缘电介质构成.当在两金属电极间加上一定电压时，电极上就会存储一定量的电荷，所以电容器是一种储能元件.由于电容器的广泛应用，电容一直是高中和大学物理重点教学内容之一.平行板电容器作为电容器的典型代表，常用来探究电容器串并联规律.本文从平行板电容器串并联的两道典型例题出发，利用静电平衡后金属板是等势体这一结论分别研究电容器串联和并联.教师在教学过程中充分强调该结论的重要性，有利于学生在以后处理类似问题中避免错误.

1 电容器的并联

平行板电容器的电容C=ε0εrS／d，其中ε0是真空电容率，εr为相对电容率，S是平行板的面积，d是两极板之间距离.电容的大小仅与导体的形状、相对位置、其间的电介质有关，与所带电荷量无关.对于电容器的并联知识点，课本明确地给出两个电容器C1和C2并联后的电容C总=C1+C2.典型例题如下.

例1.一平行板长为l，宽为m，间距为d的电容器（如图1 所示），两板分别带有+Q和-Q的电荷.先将一块长为x，宽为m，间距为d，相对电容率为εr的电介质插入其中，在忽略边界效应的情况下，试求电容器的电容以及中心P点的电场强度E的大小.

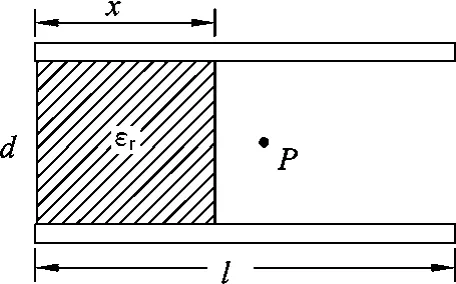
图1

解析：对于第1问，学生很容易得出正确结果

而这一看似完美的结论却是错误的.其原因是误认为两极板上的电荷分布是不变的.这样则会导致金属极板左右两端电势差（U=Ed）不等.金属中电势差的存在必然导致板内的自由电子发生移动直到静电平衡为止.因此两极板之间的电场强度肯定会发生改变.显然达到静电平衡后导体是等势体，两极板的左端和右端的电势一定相等.

正确解法：利用（1）式得到电势差U后即可得到电场强度

当然这个问题还可以利用电荷密度与电场强度的关系和电荷守恒定律联合求解，但是前提条件需要弄清楚电场强度分布，因此还得知道静电平衡后导体是等势体，两极板之间的左右两段的电势差相等.

2 电容器的串联

例2.忽略边界效应，求图2（a）所示的电容.如果在两种电介质间放置一块薄金属板后电容是否变化？

图2

解析：可以利用等效电容串并联法来处理该问题.［1］首先，建立如图2 所示的坐标，会发现相对电容率为εr1和εr2的电介质厚度随x的变化关系分别为

在两种电介质接触面放置一块薄金属板后，即使上下两极板充相同电荷量，中间的金属板也不会带电，对电容上下极板电势没有影响，故电容器的电容没有变化.实际上，只要我们仔细观察就会发现，在两种介质的接触面上未放金属板之前，它不是一个等势体.如果放入金属板以后，金属板自始至终是一个等势体.静电平衡后导体表面的电场垂直导体表面，电容之间的电场分布就会改变，因而两极板之间的电势差可能改变.因此，放入金属板可能对电容会有影响.我们将电介质为εr2的部分简化成图2（b）所示的电容.该电容是非平行板电容.通过电势的拉普拉斯方程以及利用电场强度等于电势的负梯度这一规律，很容易发现如果两极板上带有电荷，电场线是以O点为圆心的圆弧线，同一电场线的电场相同.求解该电容为［2-5］

同理我们可得电介质为εr1部分的电容

因此串联后总的电容为

3 结论

静电场中的导体和电介质一直是物理教学的重点内容之一，也是难点之一.学生在学习电容过程中，学生往往足够重视电介质对电容和电场的影响，而对于导体对电容的影响关注不足，从而导致一些问题.本文从两道典型例题出发，充分体现了金属静电平衡后为等势体这一重要结论对电容知识点学习的重要性，进一步完善学生的知识结构.最后，期望这些分析为以后的相关教学提供一些帮助.