谐波传动空间相伴运动的共轭理论与特性分析
2022-11-03董博董惠敏王德伦张楚
董博,董惠敏,王德伦,张楚
(大连理工大学机械工程学院,辽宁大连 116024)
谐波齿轮传动在刚性轮齿假设条件下,对于杯型柔轮(一般谐波传动都是杯型柔轮)轮齿间的相对运动在柔轮波发生器作用下属于轴线倾斜的空间共轭运动.目前,谐波齿轮传动轮齿共轭运动的常用方法是采用轴线平行的平面共轭理论进行分析和对主截面进行平面齿形设计[1-9].但针对由柔轮空间变形引起的轮齿的空间啮合造成的其他截面的干涉,王家序等[1]通过线性关系改变柔轮齿根处的壁厚实现其他截面的无干涉啮合,并在后续的改进中[2-4]通过合理调整柔轮齿径向位置的方法,实现空间无干涉啮合;范元勋等[5]和Yu 等[6]通过改变壁厚和修改变位系数方法实现其他截面的无干涉啮合;Dong等[7-9]采用离散方法将空间问题离散为若干平面问题,建立瞬心线法研究轮齿的三维共轭运动,论证了轮齿共轭齿廓应为三维空间曲面.以上的研究为谐波齿轮传动的空间啮合运动提供了可行的研究思路与方法,但均将谐波传动轮齿的空间相对运动问题简化为平面运动问题,以截面齿形代替空间齿形或是对其进行修正.虽然,以平面共轭运动近似处理谐波传动的空间共轭运动不失为一种简单的处理方法,但并非谐波齿轮传动的真实共轭运动,难以揭示轮齿运动的本质.为此,本文从根本上考虑谐波传动柔轮壳体的空间弹性变形,研究轮齿的空间共轭运动及其特性,为空间齿形设计和强度与寿命研究[10]奠定理论基础.
在谐波齿轮传动中,轮齿视为刚体,由于刚体的空间相对运动可以描述为与刚体分别固连的瞬轴面的滚动和滑动[11-12],因此轮齿的相对运动可以分解为绕瞬轴的转动和沿瞬轴的移动,其瞬轴面能够表示刚性轮齿的空间相对运动,隐含了刚性轮齿空间运动的内在信息.相伴方法是刚体相对运动分析中的一种常用方法[13],以瞬轴面为原曲面,刚性轮齿的齿面为瞬轴面的相伴曲面,采用相伴方法研究瞬轴面与共轭齿面间的内在联系,能够直接揭示刚性轮齿空间相对运动的本质.
为了研究谐波齿轮传动轮齿的空间真实啮合运动,本文提出一种基于相伴方法的谐波传动空间共轭运动模型.将刚/柔轮齿面的相对运动转化为瞬轴面的滚动与滑动,采用瞬轴面和一对共轭齿面的相伴运动方法,推导出谐波传动空间共轭条件式,进而建立瞬轴面与共轭齿面相伴运动的共轭模型;通过所建立的空间共轭模型,分别研究了瞬轴与共轭点法矢的关系特性、空间共轭的退化与约束特性、啮合面为准不动面的空间共轭特性;最后通过实例仿真对空间共轭模型与运动特性进行了验证,为谐波传动的空间共轭理论提供了一种新的共轭运动分析方法.
1 轮齿空间运动的动定瞬轴面
1.1 柔轮壳体中性层母线上的坐标系
谐波传动由波发生器、刚轮和柔轮3 个构件组成,通常刚轮固定,波发生器输入,柔轮输出,其空间运动分析基于3种基本假设:
1)柔轮齿刚性不变形,仅在齿槽中部发生变形.
2)柔轮壳体变形时,柔轮杯底不变形.
3)柔轮壳体中性层与轮齿对称面的交线为一条直线(母线),且相对杯底做三维空间运动.
根据假设,柔轮壳体中性层母线的空间运动是由柔轮啮合端的弹性变形约束及杯底的不变形约束共同确定的.在啮合端,由壳体的半无矩理论可知,其径向位移w、周向位移v、法向转角μ和轴向位移u是关于转角φ(柔轮啮合端相对波发生器长轴转角)函数.因此,在杯底不变形约束条件下,由柔轮齿啮合端中性层母线与齿宽中截面交点的径向位移w、周向位移v、法向转角μ和轴向位移u由壳体的半无矩理论可得:

式中:w0为柔轮变形时的最大径向变形量(w0=mc*,m为模数,c*为径向变形系数);rb为柔轮中性层变形前的半径;l0为中性层母线与齿宽中截面交点距杯底的距离.


表1 谐波传动运动参数Tab.1 Motion parameters of harmonic drive
根据谐波传动原理,谐波传动刚性轮齿的输入、输出的转角满足:
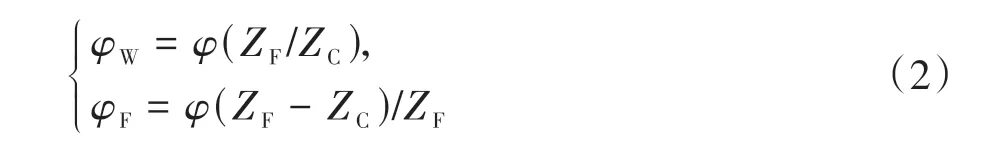
式中:ZF为柔轮齿数;ZC为刚轮齿数.
式(2)建立了各转角与变量φ之间的函数关系φW(φ)、φF(φ).
1.2 中性层母线的直纹面运动
以刚性柔轮齿固连的中性层母线Lk为参考直线,则参考直线Lk与齿宽中截面的交点为Of,其空间运动轨迹形成直纹面∑k,如图1 所示,则在坐标系SF下的直纹面的矢量方程可表示为:
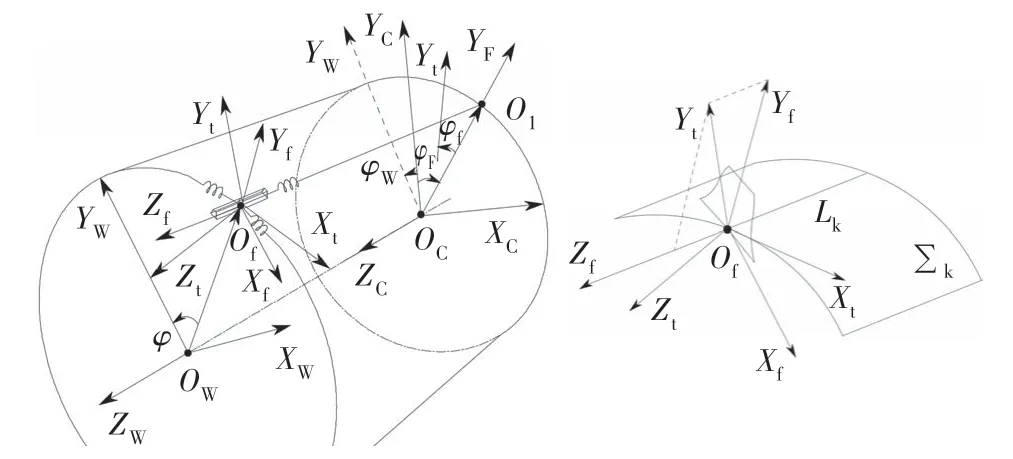
图1 谐波传动空间坐标系Fig.1 Spatial coordinates of harmonic drive

式中:if、jf、kf分别为坐标系Sf的单位方向矢量;iF、jF、kF分别为坐标系SF的单位方向矢量.
式(3)~式(5)建立了各坐标系间的位置关系及中性层母线的直纹面方程.
1.3 轮齿的动定瞬轴面
刚性轮齿的空间相对运动可以描述为与轮齿分别固连的瞬轴面的滚动与滑动,若直线Ls恰为轮齿空间相对运动的瞬时运动螺旋轴(瞬轴ISA),则直线Ls需满足准不动条件[21]:直线上各点Pi的速度相等;方向沿着直线方向不变.
从而满足dlC/dφ=0(速度相等)(方向不变).瞬轴Ls在SC下的运动轨迹形成定瞬轴面ГC,如图2 所示,由准不动条件①可求得瞬轴的单位方向矢量为:

图2 中性层母线的直纹面与瞬轴面Fig.2 Ruled surface of neutral layer generatrix and axode
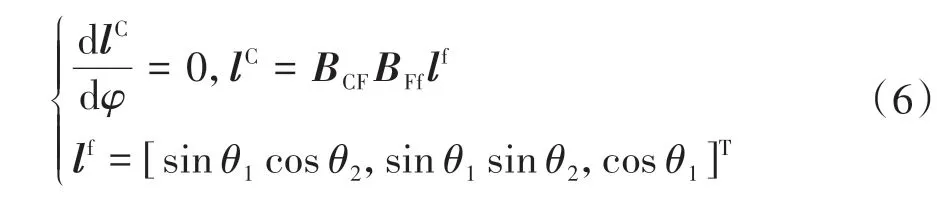
式中:lf、lC分别为瞬轴在Sf、SC下的单位矢量;θ1、θ2为矢量lf在Sf下的方向角,θ1为矢量lf与Zf轴之间的夹角,θ2为Xf轴与矢量lf在坐标平面Of-XfYf上投影矢量的夹角.
将式(4)、式(5)中的BCF、BFf代入式(6),可获得两个独立标量方程,因此可求出瞬轴的方向lC与变量φ之间的关系(θ1(φ)、θ2(φ)).
由准不动条件②可求得瞬轴的位置矢量为:
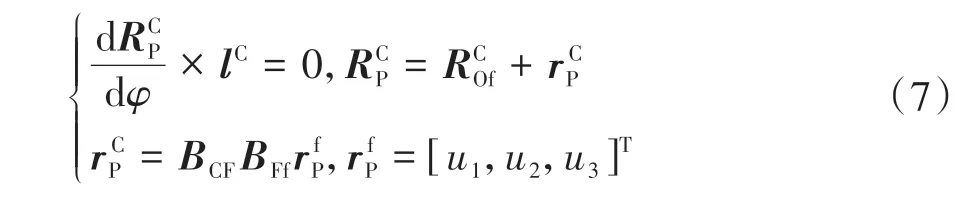
式中:为瞬轴上P点在SC下的矢量;为瞬轴上P点在Sf下的矢量;u1、u2、u3为P点在Sf下的相对坐标分量.
将式(6)中的θ1(φ)、θ2(φ)代入式(7),可获得3个标量方程,因此可求出瞬轴的位置矢量与变量φ之间的关系(u1(φ)、u2(φ)、u3(φ)).联立式(6)和式(7)可获得Sf下的动瞬轴面Гf、SC下的定瞬轴面ГC.动定瞬轴面可表示为:

式中:λC为定瞬轴面ГC的直母线参数,λf为动瞬轴面Гf的直母线参数.
2 空间相伴运动的共轭模型
2.1 齿面与瞬轴面的相伴运动
以动瞬轴面Гf和定瞬轴面ГC为原曲面,则柔轮刚性齿面Cf与刚轮刚性齿面CC分别为Гf和ГC的相伴曲面,如图3 所示.由于瞬轴面的腰线具有唯一性,能够反映出瞬轴面的几何特征,因此由公式(8)可得以腰线为准线的动定瞬轴面可表示为:
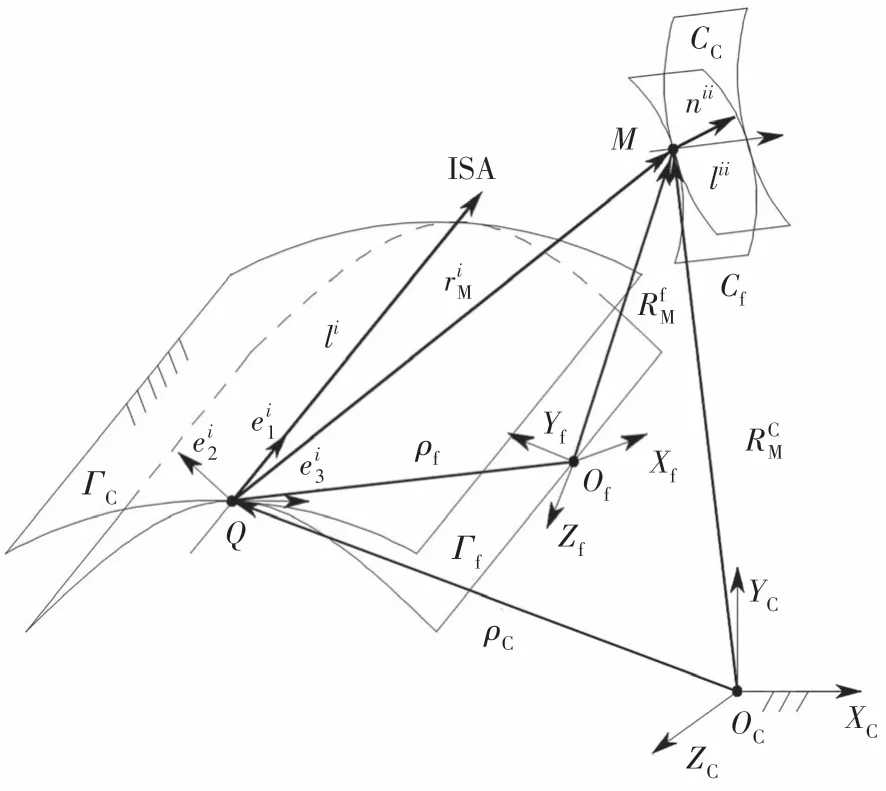
图3 刚性齿面与瞬轴面的相伴运动Fig.3 Concomitant motion of rigid tooth surfaces and axodes
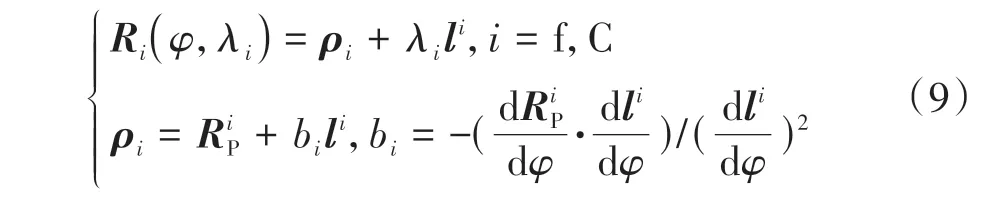
式中:ρi为瞬轴面的腰线在Si下的矢量;bi为腰准距.
式(9)建立了瞬轴腰线ρi及腰准距bi与变量φ之间的函数关系(ρi(φ)、bi(φ)).


在刚性齿面的假设条件下,设轮齿齿面Ci为直纹面,齿面Ci上的点M在轮齿坐标系Si下的位置矢量为,直纹面上的M点在Frenet 标架下的位置矢量为,轮齿齿面直母线的方向矢量在Frenet标架Si下为lii,轮齿齿面在M点处的法矢在Frenet 标架Si下为nii.由于瞬轴面Гi与轮齿齿面Ci为两个相伴曲面,因此在轮齿坐标系Si下齿面Ci的位置矢量Rii可表示为:

式中:u1、u2、u3为M点在Frenet 标架Si中的相对坐标分量;l1、l2、l3为方向矢量lii在Frenet 标架Si中的相对坐标分量;n1、n2、n3为M点处的法矢nii在Frenet 标架Si中的相对坐标分量.
式(11)建立了齿面与瞬轴面的相伴运动关系.
2.2 基于相伴方法的共轭条件
由空间共轭基本原理可知,啮合点处的相对运动速度在齿面公法线方向的投影为零,结合2.1节齿面与瞬轴面的相伴运动,则齿面上共轭点的相对运动速度可表示为:
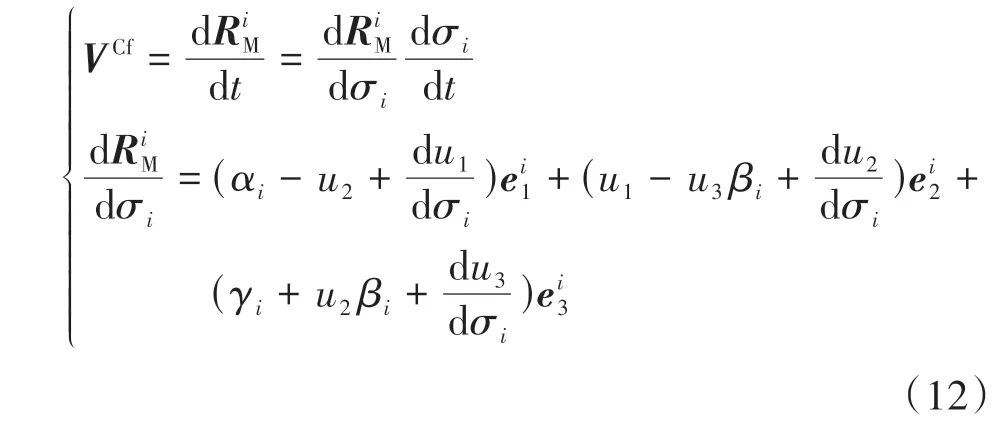
将式(11)与式(12)代入nii·VCf=0,可得基于相伴运动的齿面共轭条件式为:
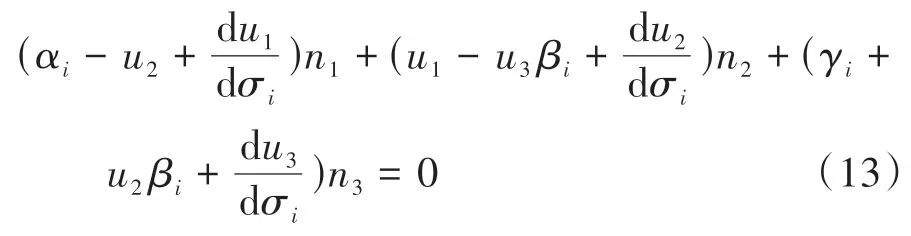
共轭条件式(13)由瞬轴面的结构参数(αi、βi、γi)、共轭齿面参数(u1、u2、u3、l1、l2、l3)及齿面微分参数(du1/dσi、du2/dσi、du3/dσi)三部分组成,通过共轭条件式(13)建立了瞬轴面与共轭齿面之间的内在联系,能够清晰明了地表达出采用相伴方法的空间共轭运动机理.
2.3 共轭方程及共轭齿面求解方法
共轭齿面的接触线lii在Frenet 标架Si下的运动轨迹形成啮合面,啮合面上任意点只要满足共轭条件式(13)便能成为共轭点,因此联立式(11)与共轭条件式(13),可得共轭齿面的共轭方程为:
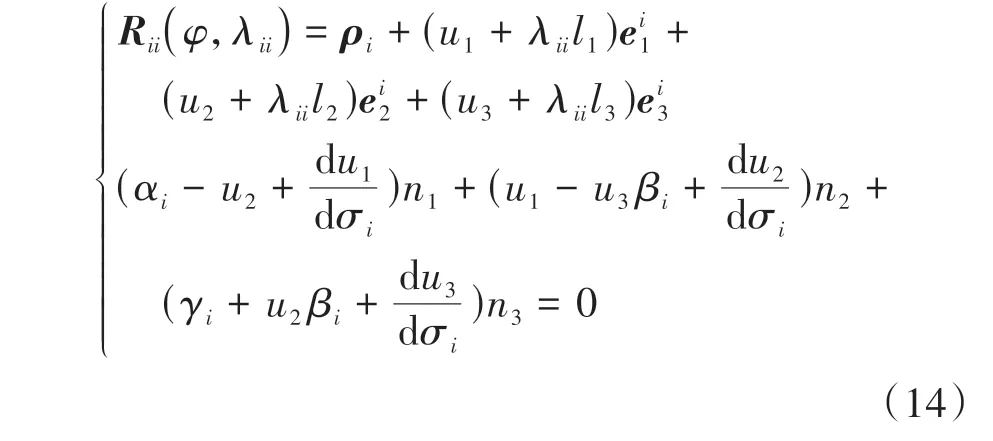
式(14)建立了满足相伴运动共轭条件的共轭齿面方程,并清楚表达出了在Frenet标架Si下的啮合面的方程,在Frenet标架Si下的啮合面可作为连接瞬轴面与共轭齿面的桥梁.
谐波传动空间共轭齿面的求解问题可以概述为3 类基本求解问题:第1 类是已知一对轮齿的其中一个(刚轮或柔轮)齿面及运动规律,求啮合面及另一与其共轭的齿面;第2 类是已知啮合面及运动规律,求空间共轭的一对轮齿(刚轮和柔轮)齿面;第3 类为已知一对轮齿的其中一个(刚轮或柔轮)齿面及啮合面,求运动规律及另一共轭柔轮(或刚轮)齿面.以第2类问题为例,说明共轭齿面的求解方法:
1)已知在Frenet 标架Si下的一个啮合面Ti,根据式(11)确定啮合面的位置矢量、方向矢量lii及法向矢量参数nii;
2)联立式(1)~式(8),并代入瞬轴面式(9)确定瞬轴面的腰线矢量ρi(φ)及瞬轴方向矢量li(φ);
3)将腰线ρi(φ)及方向矢量li(φ)代入式(10),求得瞬轴面的结构参数(αi、βi、γi);
4)将瞬轴面的结构参数(αi、βi、γi)、啮合面参数(uj、lj、nj,j=1,2,3)及齿面微分参数(duj/dσi)代入共轭条件式(13),求得啮合面参数所对应的运动参数φ值;
5)将运动参数φ值代入式(14),求得空间共轭的刚轮齿面CC及柔轮齿面Cf.
3 空间相伴共轭运动的特性
3.1 瞬轴与共轭点法矢的关系特性
由于空间任意一点处的相对速度和这个点绕瞬轴做一定的螺旋运动时的线速度相同,因此,当空间共轭齿面的接触线在任意瞬时均为直线时,在任意瞬时接触线上任意一点的相对速度均等于该点绕瞬轴做一定螺旋运动时的线速度.相对速度可表示为(ωl为啮合点的相对速度绕瞬轴的回转角速度,vl为该点的相对速度沿瞬轴的滑动速度),将其代入空间共轭基本原理公式nii·VCf=0可得:

3.2 空间共轭退化为平面共轭的约束特性

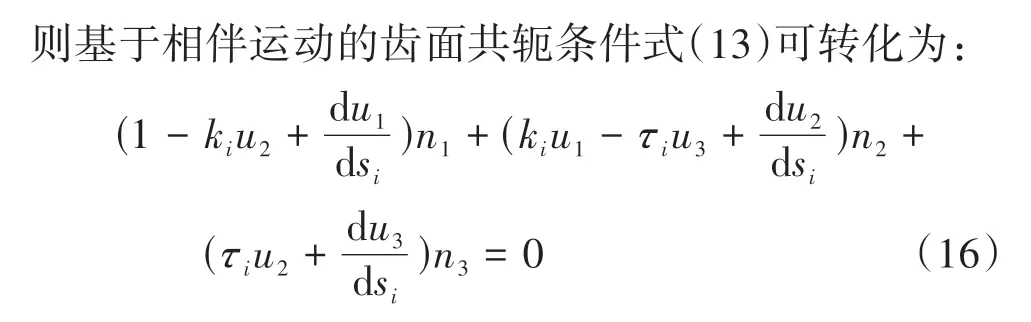
谐波传动轮齿的空间共轭运动退化为平面共轭运动后,动定瞬轴面(退化为两柱面)及共轭齿面在其直母线方向(Zi轴方向)不产生运动,仅在平面XiYi内运动,由式(15)可知,退化为平面共轭运动后,共轭齿面法矢nii与啮合点位置矢量共线且瞬轴相交于Q点,退化后的空间共轭运动在平面XiYi内的投影如图4所示.
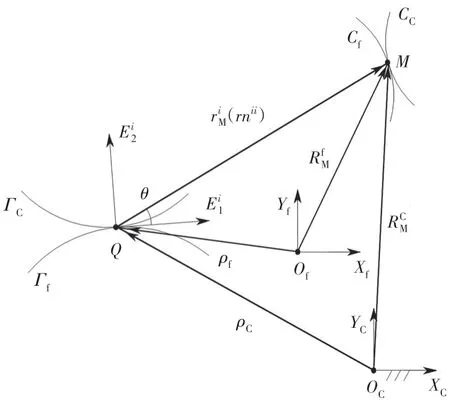
图4 空间共轭退化后的平面相伴运动Fig.4 Plane concomitant motion after space conjugate degeneration
设(ri,θ)i为啮合点M在下的极坐标位置,则由公式(11)可得共轭齿面法矢nii(n1=cosθ,n2=sinθ,n3=0)及啮合点位置矢量(u1=rcosθ,u2=rsinθ,u3=0),将其代入式(16)可得退化后平面共轭运动的共轭条件为dr+cosθds=0,这与文献[15]推导的结论一致,验证了采用相伴方法的谐波传动刚性轮齿共轭条件式的正确性.
3.3 啮合面为准不动面的共轭特性
为证明本文所提出的空间相伴运动共轭模型的通用性与统一性,以啮合面为准不动面(接触线为直线且满足准不动线条件,接触线与啮合线共面)为例,通过本文第2 节内容,分析其空间共轭运动特性.如图5所示,由于啮合面为平面Ti,设过瞬轴面腰线上的Q点做啮合面Ti的垂线并与啮合面相交于M点,则啮合面Ti上的M点在Frenet标架Si下的位置矢量可表示为,其中,p为瞬轴面腰线上的Q点到啮合面Ti的距离,当啮合面Ti为准不动面时代入准不动面条件可得:dn1/dσi=n2,dn2/dσi=-n1+βin3,dn3/dσi=-βin2,dp/dσi=-αin1-γin3,设C、D分别为异面直线li与nii公垂线的垂足,在Frenet 标架Si下C点及D点的位置矢量可表示为,且满足,与齿面共轭条件式(13)联立可得
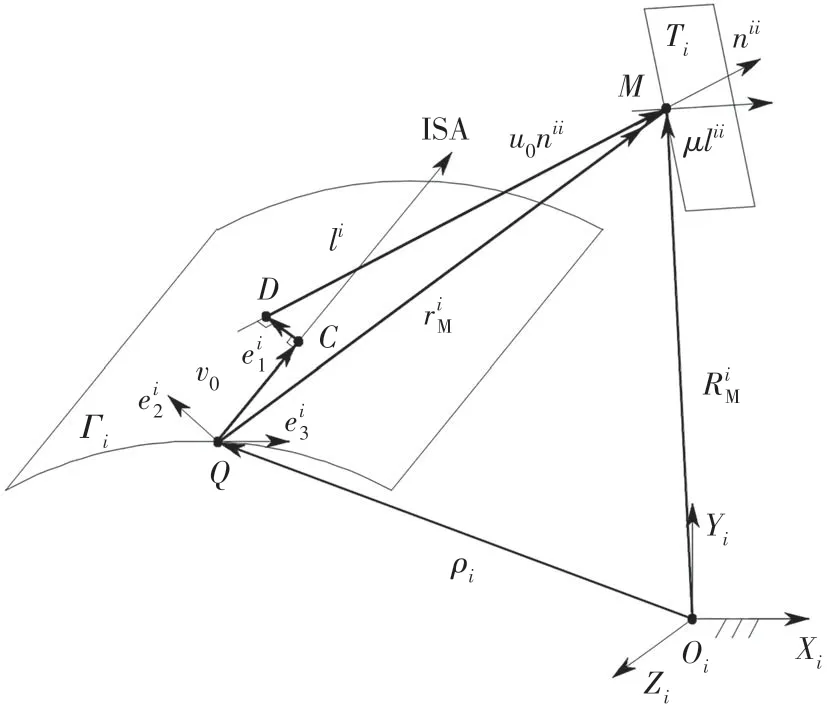
图5 啮合面为准不动面的相伴运动Fig.5 Concomitant motion of meshing surface with quasi-fixed surface
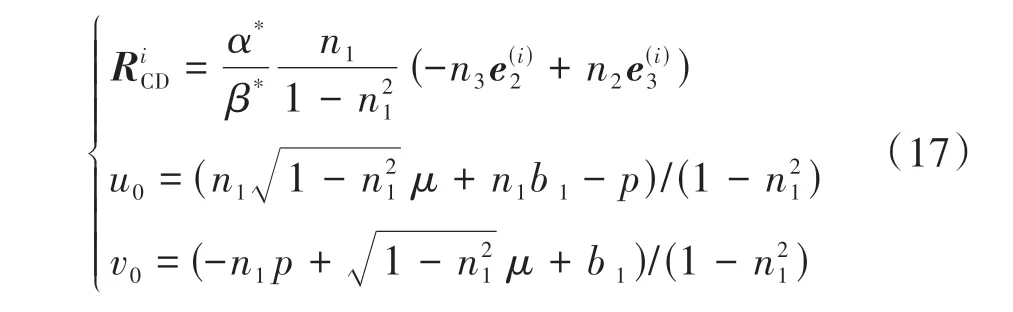
式中:α*、β*为动定瞬轴面的诱导结构参数,且α*=αCαf,β*=βC-βf.
3.4 实例仿真验证
实例采用凸轮的外轮廓线为余弦曲线的波发生器,刚轮固定、波发生器输入、杯型柔轮杯底输出,谐波传动结构如图6 所示,仿真参数如表2 所示.基于本文所建立的瞬轴面的空间相伴共轭方法,采用MATLAB 编程对谐波传动的空间运动进行仿真分析,以检验该方法的准确性.运动参数φ的取值范围为φ∈[-π/2,π/2],以表2 的具体参数仿真轮齿的共轭相伴运动,仿真结果如图7所示.
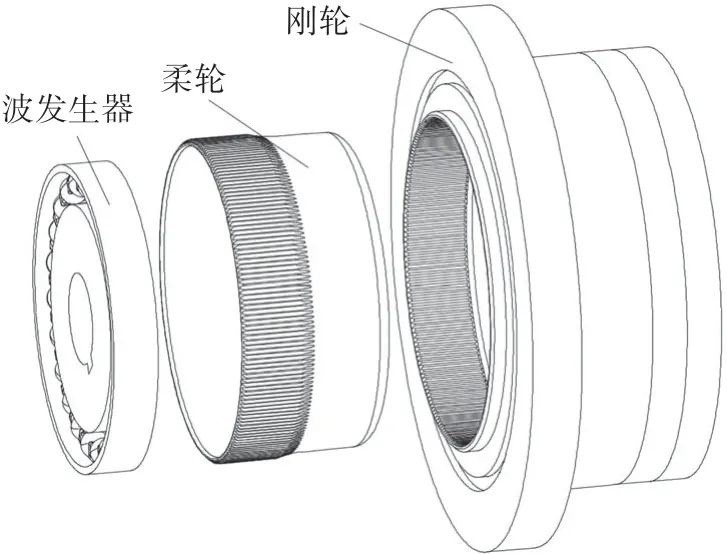
图6 谐波传动结构图Fig.6 Structural diagram of harmonic drive
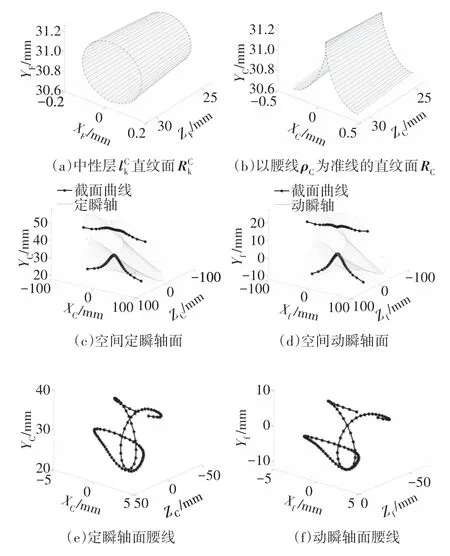

图7 轮齿空间相伴运动的仿真结果Fig.7 Simulation results of spatial concomitant motion between gear teeth

表2 仿真参数Tab.2 Simulation parameters
由图7(a)和图7(b)可知:中性层母线在SC下的直纹面关于平面XCYC对称,形状为柔轮壳体齿宽前端尖装、齿宽后端尖装变凸的特殊曲面;中性层以腰线ρC为准线的直纹面RC同样关于平面XCYC对称,RC与为不同准线下同一直纹面的不同描述.由图7(c)~图7(l)可知:
1)退化前瞬轴的运动为空间运动,退化后瞬轴的运动为平面运动;
2)退化前后截面均呈现沿Y轴对称且不封闭的轨迹线;
3)退化后在开口处存在两条沿Y轴对称交叉的渐近线,退化后的瞬轴面截面曲线与文献[16]所述平面瞬心线一致,进一步验证了本文模型的准确性;
4)空间运动与退化平面运动为2 种不同的运动,说明本文所建立的空间共轭模型的重要意义.
4 结论
本文所建立的谐波传动空间相伴运动共轭模型,能够全面考虑柔轮壳体的空间弹性运动,即符合环型柔轮的空间共轭运动的谐波传动,也适用于桶形柔轮的平面共轭运动(如复式谐波传动).本文的主要贡献有:
1)基于相伴方法建立了谐波传动空间共轭运动模型,以瞬轴面为原曲面,刚性齿面为相伴曲面,推导出基于相伴运动的齿面共轭条件式,建立了瞬轴面的结构参数与共轭齿面参数之间的内在联系,几何意义明确,简明直观.
2)通过瞬轴与共轭齿面法矢的关系特性与分析表明:啮合点的公法线与瞬轴垂直相交的充要条件为混合积(nii,li,)为零,瞬轴与啮合点的公法线垂直并相交是空间共轭的一个特例.
3)通过空间共轭退化为平面共轭的约束特性与分析表明:谐波传动刚性轮齿的平面运动为空间运动退化后的一种特殊运动,退化后的空间运动的瞬轴面截面曲线与平面运动的瞬心线一致,由此可知空间运动退化后的运动与平面运动一致,模型对一般谐波传动和复式谐波传动具有适应意义.
4)通过啮合面为准不动面的共轭特性与分析表明:对于空间共轭齿面,当啮合面为准不动面时,在任意共轭瞬时,其接触线上任意点的法矢与瞬轴夹角相等,且接触线上任意点的法矢与瞬轴公垂线的距离恒定.
