基于数值分析理论的低复杂度MED 算法

杨喜，田冲，方如意，刘泽宇，张银行，雷可君†

（1.吉首大学信息科学与工程学院，湖南吉首 416000；2.中南大学计算机学院，湖南长沙 410100）

随着物联网（IoT）、5G等无线通信技术的快速发展，现有频谱资源正变得日益匮乏.传统频谱分配方案在特定时间、区域将特定频带固定分配给授权用户使用.然而，由于业务使用的不均衡性，这种固定的频谱分配方式将不可避免地导致部分频带陷入拥堵而部分频带处于空闲的状况，从而严重影响频谱使用效率.为此，文献［1］提出利用认知无线电（Cognitive Radio，CR）技术来提升现有频谱资源的利用效率.CR 是指一个能够不断进行频谱感知、动态辨别并能对空闲的授权频带进行频谱接入的无线电系统［2］.在该系统中，次级用户（Secondary User，SU）能通过未被主用户（Primary User，PU）占用的频带进行通信，同时保证不对PU 之间的通信造成干扰.为此，SU 需要采用频谱感知技术以可靠地检测目标频段上主用户信号是否出现，进而判断能否接入该频段［3］.

经典的频谱感知算法包括匹配滤波检测（Matched Filtering Detection，MFD）［4］、能量检测（Energy Detection，ED）［5］以及基于特征值的检测［6］.当PU 信号及噪声信号信息完全已知且SU 与PU 之间同步时，MFD 具有最佳的检测性能.然而，SU 在检测过程中很难获得上述信息，且在低信噪比条件下极难做到信号同步.ED 算法是一种经典的半盲检测算法，其不需要PU 信号及同步信息，且工程实现简单，对噪声方差已知的独立高斯信号具有最优的检测性能.但在实际应用中，ED 检测性能受噪声不确定性现象和信号相关性的影响很大.文献［7］和文献［8］的研究表明，当存在噪声不确定性或信号高度相关时，ED 的检测性能将显著下降.得益于随机矩阵理论的快速发展，近年来基于特征值的检测方法引起了研究者的广泛关注.文献［9］提出了一种基于取样协方差矩阵最大特征值的半盲检测算法.该算法利用取样协方差矩阵最大特征值构造判决量，利用高维随机矩阵中Tracy-Widom 分布计算判决门限.由于取样协方差矩阵很好地捕捉了多天线信号的相关性，因此基于最大特征值的检测算法在检测高相关信号时表现出比ED 算法更为优异的检测性能［9］.文献［10］的结论进一步表明最大特征值检测实际上是在最大化多天线输出信噪比条件下的最佳检测器形式.值得一提的是，通过对噪声方差进行估计，可以进一步得到不同场景下各种基于最大特征值的全盲检测器形式［11-13］.正是由于上述优点，MED 算法成为认知无线电中相关信号频谱检测场景中广泛关注的半盲检测方法.

MED 算法涉及取样协方差矩阵的特征值计算，以及给定目标虚警概率下判决门限的计算.然而，前者要求进行矩阵特征值分解，而后者则包含复杂微分方程的求解、复杂函数的积分及方程求解运算［9，14-16］.以上两部分的计算量都非常大，对频谱感知的时限性要求提出了极大的挑战.同时非常不利于工程实现的需要.特别是随着CR 与5G、IoT 等技术的融合［17-20］，将来的频谱感知场景中的接收信号通常呈现高维特征.这一新特征将导致传统的MED算法的运算量和实现复杂度急剧上升而难以实际应用.令人遗憾的是，目前的工作仍集中在低维场景中算法检测性能的研究，而对高维条件下算法的高效实现尚未见诸报道.对于MED 算法中特征值的计算，尽管文献［15］提出了一种基于幂法的计算方法，然而该方法在高维信号及低信噪比条件下存在收敛速度慢的问题.此外，门限的计算涉及复杂的逆Tracy-Widom 分布函数计算，而该逆函数目前尚无明确的解析表达形式［21，22］.因此，目前的研究均需依赖专用软件计算得出一些有限的离散值，然后利用查表的方法获得一些常用目标虚警概率PFA所对应的判决门限值.然而在实际的感知应用中，往往需要根据实际情况灵活确定目标虚警概率值［23-25］，此时获得这些新的PFA值所对应的门限值将不得不面临复杂的计算问题.

如何有效解决感知判决量和判决门限的计算难题，设计出相应的低复杂度算法，对于解决高维场景下MED 的高效频谱感知具有极其重要的应用价值.有鉴于此，本文基于数值分析的理论，提出一种结合Rayleigh 商加速幂法和三次样条插值法的最大特征值检测算法.新算法在保持优良检测性能的同时显著降低了特征值和判决门限的计算复杂度，有效提高了计算效率并有利于后续的硬件实现.

1 经典MED算法及其面临的计算问题

假定认知节点配置的天线数量为M，并对多天线接收信号进行N次连续采样.设第n次采样得到的接收信号向量为x(n)=[x1(n)，x2(n)，…，xM(n)]T，这里n=1，2，…，N.若存在PU 信号，则实际接收信号为PU信号与噪声信号的叠加，即有：

式中：s(n)表示经过无线信道接收到的PU 信号向量，η(n) 表示M维加性高斯白噪声向量.标记η(n)～NM(0，)，其中I为单位矩阵为噪声功率.不失一般性，通常假定PU 信号与噪声信号之间统计独立.相应地多天线频谱感知问题在数学上可以表示为如下二元假设检验问题：

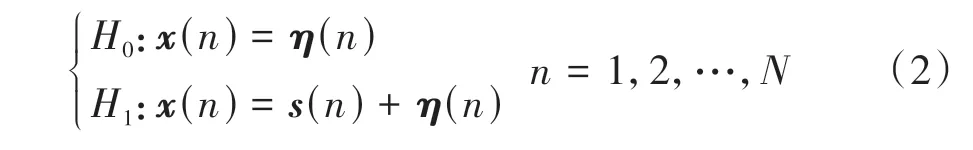
式中：H1表示PU 信号存在，H0则表示PU 信号不存在.有必要指出，上述模型同样适用于协作式频谱感知问题，此时M相应代表参与协作的认知节点数目.由M根天线的接收信号可以形成如下M×N维接收信号矩阵：

则接收信号的取样协方差矩阵可以表示为

式中上标T 表示转置运算.引入如下归一化取样协方差矩阵：

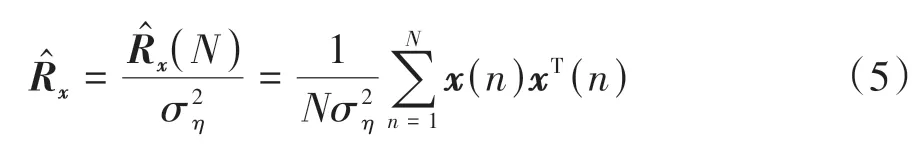
经典的MED 算法流程可以归纳如下.首先，计算取样协方差矩阵(N)的最大特征值λmax，并由此计算感知判决量λMED=λmax/（实际上λMED即为归一化取样协方差矩阵的最大特征值）；其次，根据随机矩阵理论中Tracy-Widom 分布理论计算感知判决门限γMED；最后，认知节点实施感知判决：若λMED≥γMED，则判定PU信号存在；反之，则判定PU信号不存在.其中，给定目标虚警概率PFA条件下判决门限的计算表达式为［9］：

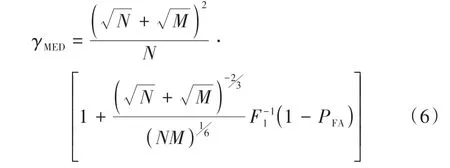
式中：(·)是1 阶Tracy-Widom 分布的累积分布函数F1(·)的逆函数.由于数学分析的复杂性，目前尚未找到(·)的显式解析表达式.因此，(1 -PFA)的值需通过解方程F1(x)=1 -PFA才能获得.注意到F1(x)定义为：

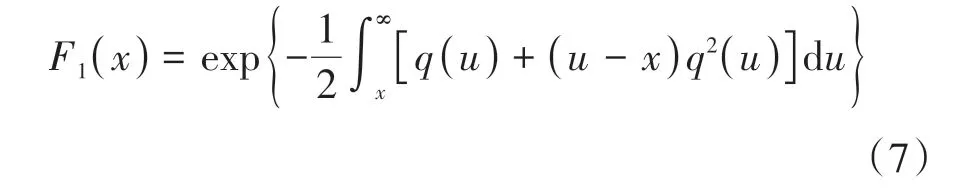
式中：q(u)表示Painlevé 函数，其定义为如下非线性Painlevé微分方程的解：

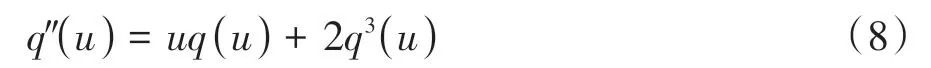
从上面的分析可知，经典MED 算法的计算复杂度主要来自于最大特征值和判决门限的计算.现有的MED 算法在计算最大特征值时采用特征值分解或者幂法求解.基于特征值分解的方法需要计算的所有特征值，其计算效率低下，不适于感知判决量的快速计算的需要.相对于特征值分解而言，尽管幂法在一定程度上提高了计算效率，但是该方法在高维接收信号条件或低信噪比条件下计算量将急剧增加.另一方面，由于目前尚无(·)的解析表达式，现有的工作需联立式（8）和式（9）以确定判决门限.该过程涉及二阶Painlevé 微分方程的求解、Painlevé 函数q(u)的复杂积分和指数运算，以及给定PFA条件下复杂方程的求解.显然，以上两部分的计算需消耗大量计算资源及计算时间.一方面，这对于处理能力有限的认知节点而言显然难以承受，另一方面，认知无线电对于频谱感知有严格的时间限制，大量的计算将导致无法满足频谱感知的时限性要求.

2 基于数值计算理论的低复杂度MED算法

本节结合Rayleigh 商加速幂法和三次样条插值方法，提出一种基于数值计算理论的低复杂度MED算法.2.1和2.2小节将针对上述两个方面分别展开.

2.1 Rayleigh商加速幂法计算感知判决量

传统MED 算法采用特征值分解的方法计算判决量，其计算复杂度高［14］.注意到判决量只需用到归一化取样协方差矩阵的最大特征值，因此文献［15］采用幂法计算最大特征值以降低复杂度.注意到是M阶实对称矩阵，故由矩阵理论可知有M个线性无关的特征向量xi=[xi1，xi2，…，xiM]T（i=1，2，…，M）.相应地有=λixi，其中λi是对应于特征向量xi的特征值.不妨假设|λ1|＞|λ2|≥|λ3|≥…≥|λM|，则有λMED=λ1.设v0是任意给定的非零向量，则其可以唯一地表示为：

这里不妨设α1≠0.构造如下向量序列：

当bk=max(uk)时，即为文献［15］所采用的幂法，这里max(uk)表示取向量uk中的最大元素.由幂法的基本理论可知，当k充分大时，有：

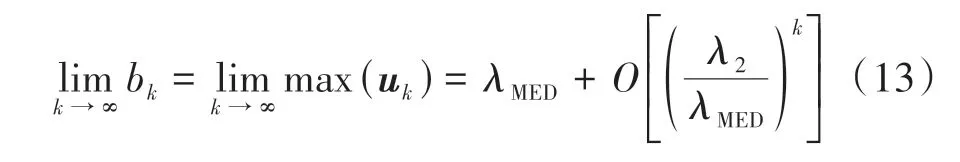
由式（13）可知利用幂法计算λMED的收敛速度取决于|λ2MED|的大小，该值越接近1 则迭代收敛速度越慢.值得注意的是，在认知无线电网络中，当主用户信号比较弱或者未出现时有→I，相应地则有|λ2MED|→1.这一情况使得幂法在低信噪比条件下的计算效率大大降低，将显著提升高维条件下MED 算法的计算复杂度.为此，本文提出一种基于Rayleigh 商加速理论计算判决量的方法.在该方法中，首先基于Rayleigh商理论构造新的迭代序列

不难证明［14］：

故当k充分大时有：

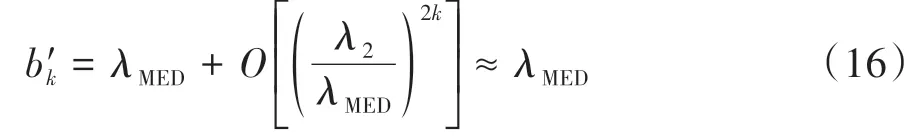
对比式（13）和式（16）不难发现，比bk能更快地收敛到归一化取样协方差矩阵的最大特征值λMED，从而可以有效提升高维条件下低信噪比或主用户信号未出现时MED 算法的计算效率.基于Rayleigh商加速幂法计算感知判决量的流程如表1所示.

表1 Rayleigh商加速幂法计算感知判决量Tab.1 Rayleigh quotient accelerated power method for computing the sensing statistic

图1 给出了信噪比SNR 分别为-29 dB、-26 dB和-15 dB，最大迭代次数K=500，误差界ε=10-4，以及天线数目M=32，64，128，256 时，文献［15］所提方法和本文所提方法的平均收敛次数对比情况.由仿真结果可知，本文所提方法比文献［15］的方法有更快的收敛速度.特别是在低信噪比条件下，这种优势将变得更为明显.与此同时，还可以看出随着信噪比和天线数目的增大，本文所提方法在高维接收条件下有着极快的收敛速度，因而非常适用于大规模多天线或者大规模协作场景中的频谱感知问题.

图1 不同信噪比时幂法与所提算法计算感知判决量的平均迭代次数对比Fig.1 Comparison of the average number of iterations between the power method and the proposed algorithm for calculating the test statistic at different signal-to-noise ratios

2.2 三次样条插值法计算判决门限

由前面的分析可知，利用现有方法计算任意给定的PFA值对应的判决门限时存在两方面的问题：（1）只能正向计算累积分布函数值F1(·)，而不能计算其逆函数(·)的值，但是判决门限的计算用到的却是(·)的值；（2）只能给出一些常用PFA值（如0.1，0.05 等），然而实际问题则可能需要用到任意PFA值所对应的门限求解.为解决上述两个难题，本节提出一种基于三次样条插值的(·)计算方法，利用该方法可以实时计算出任意给定PFA时所对应的判决门限值.

经典的插值方法包括Lagrange 插值、Hermite 插值和样条插值法［14］.其中，Lagrange 插值随着插值次数增大将出现龙格（Runge）现象，曲线两端易出现震荡，而Hermite 插值需要各节点的导数值.三次样条插值法则克服了上述缺点，且近似曲线在插值节点处连续且光滑.综合以上考虑，本文选择利用三次样条插值方法求解(t)近似曲线G(t).文献［16］利用专业软件计算了1 051 个1 阶Tracy-Widom 累积分布函数的离散值.为了兼顾插值精度与计算复杂度，通过大量的实验，本文选取其中的20 个点作为插值基点.具体的插值基点(tl，gl)如表2 所示，这里l=0，1，…，19.

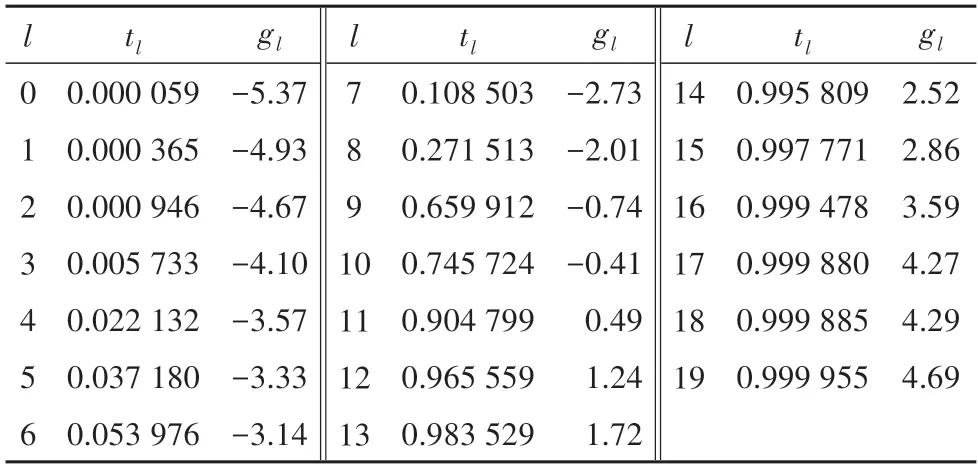
表2 插值基点Tab.2 Interpolation base points

设区间[ti，ti+1]上的三次样条插值多项式为：

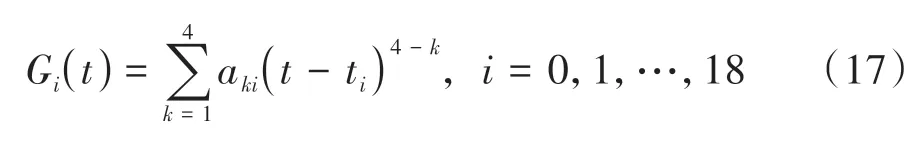
式中：aki表示三次样条插值多项式的系数.标记相邻插值基点之间的步长为

利用三次样条插值理论，基于非节点边界条件可建立如下线性方程组：

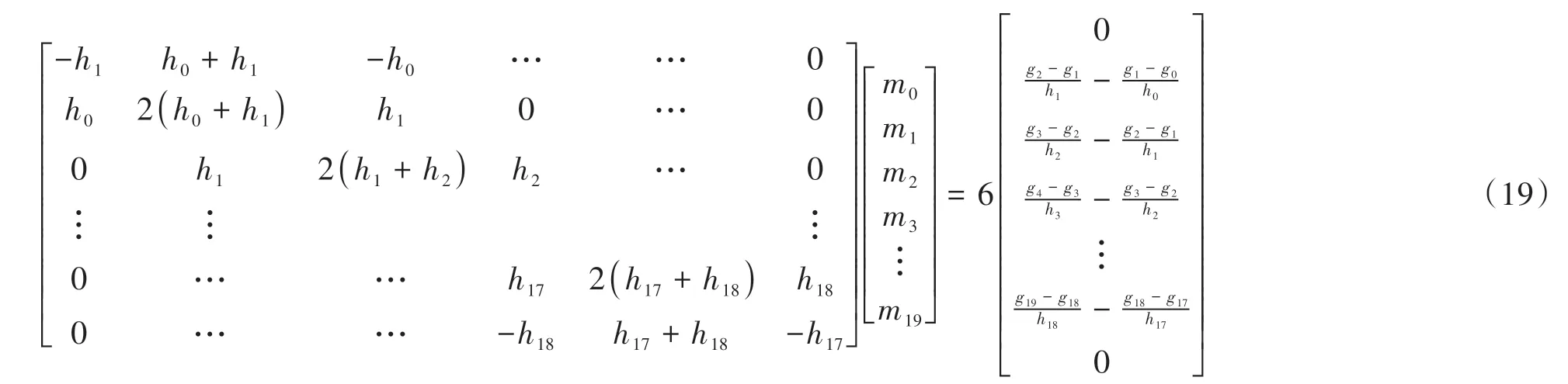
利用式（18）和表2的数据可计算得到hi，将其与gi一并代入式（19），可最终计算得到ml（l=0，1，…，19）.在此基础上，各三次样条插值函数的系数aki可计算如下：

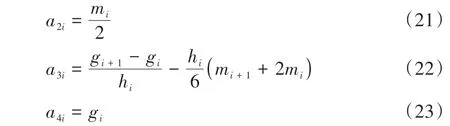
由此得到1 阶Tracy-Widom 分布的逆累积分布函数(·)的三次样条函数表达形式：

联立式（6）可得到基于三次样条插值理论的判决门限表达式：

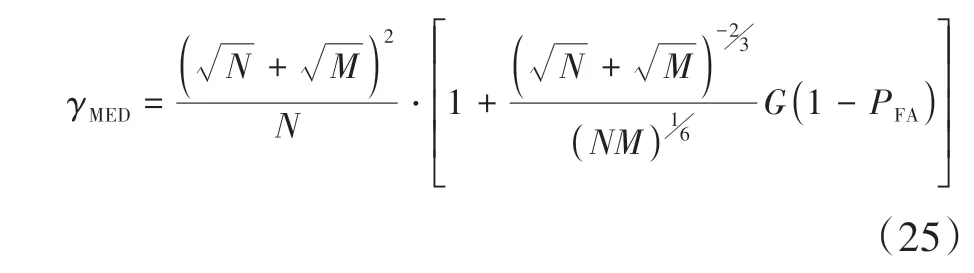
为验证本文所提算法的有效性，图2 利用文献［16］给出的1 051个点绘制了(t)的真实曲线作为比较参考基准，同时给出了利用本文提出的基于三次样条插值方法绘制的连续曲线.由图可知，G(t)与(t)吻合得非常好，由此证明了本文所提方法的正确性和有效性.

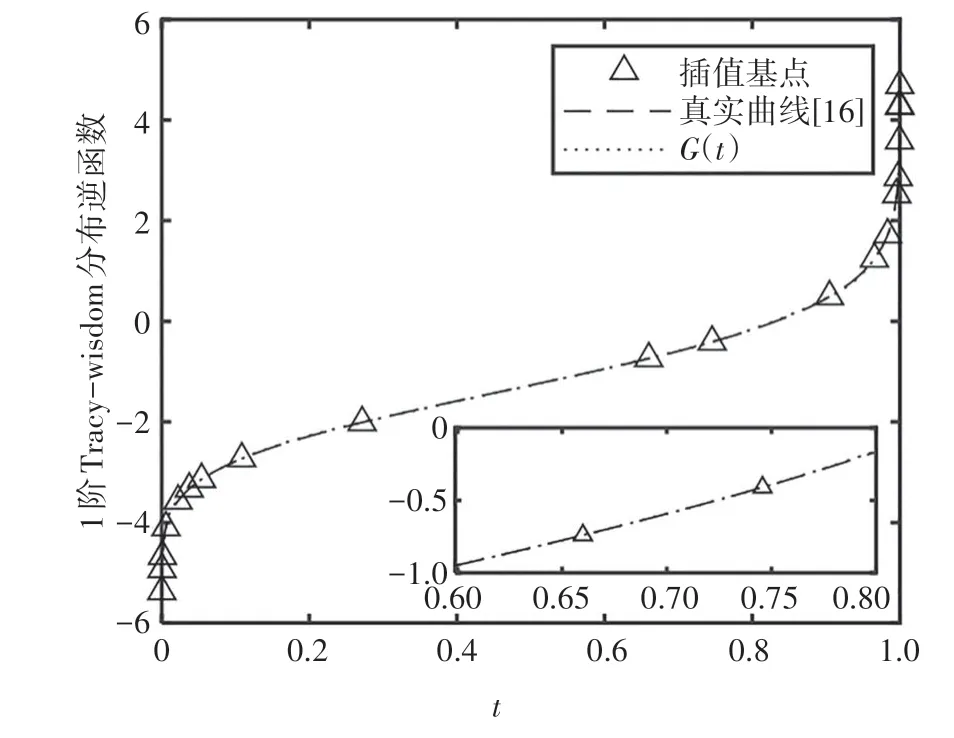
图2 三次样条插值曲线与真实值曲线比较Fig.2 Comparison between the cubic spline interpolation curve and the real value curve

2.3 基于数值分析理论的低复杂度MED算法

综合2.1 和2.2 节的结论，可以得到一种新的基于数值分析理论的低复杂度MED 频谱感知算法.新方法首先利用Rayleigh 商加速幂法计算归一化取样协方差矩阵的最大特征值，其次利用三次样条插值法计算感知判决门限，最后进行感知判决.所提算法的流程如表3 所示.由于本文所提方法可以利用式（25）直接计算判决门限值，其运算量基本可以忽略.因此，不同于经典的MED 算法，本文所提算法的计算复杂度主要来自归一化取样协方差矩阵以及最大特征值λMED的计算.其中，的计算复杂度为O(NM2)，而采用基于Rayleigh 商加速幂法的λMED计算复杂度为O(kM2)，这里k为迭代次数.故本文所提基于数值分析理论的MED 频谱感知算法总复杂度为O(NM2) +O(kM2).

表3 基于数值分析理论的低复杂度MED频谱感知算法Tab.3 Low-complexity MED spectrum sensing algorithm based on numerical analysis theories

3 检测性能分析

所提基于数值分析理论的MED 算法的计算误差来自Rayleigh 商加速幂法计算感知判决量λMED和基于三次样条插值法计算判决门限γMED两部分.表4给出了N=3 200，M=64，信噪比分别为-25 dB 至-21 dB 时采用Rayleigh 商加速幂法与文献［15］所用传统幂法计算λMED的误差情况.这里Monte Carlo 仿真次数为5 000，仿真过程中设置迭代次数为50，真实的最大特征值采用Matlab 的eig 函数计算得到（即采用特征值分解法［9］）.

由表4的结果可知，本文所提方法在计算λMED时具有很高的精度，且各项精度均明显高于传统幂法.例如，当信噪比为-21 dB时，所提方法计算结果的平均绝对误差仅为6.502 092 89×10-7，对应的平均相对误差为4.222 098 41×10-7，而此时采用幂法的对应结果则分别为4.145 751 87×10-5和2.741 964 93×10-5.此时，误差精度均提升了近2 个数量级.另外，从仿真结果不难看出，随着接收信噪比的增大，本文所提算法的计算精度显著提高.其原因在于，随着信噪比的增加，归一化取样协方差矩阵的次大和最大特征值的差别越大，使得Rayleigh 商加速幂法以更快的速度收敛，从而获得更高的计算精度.

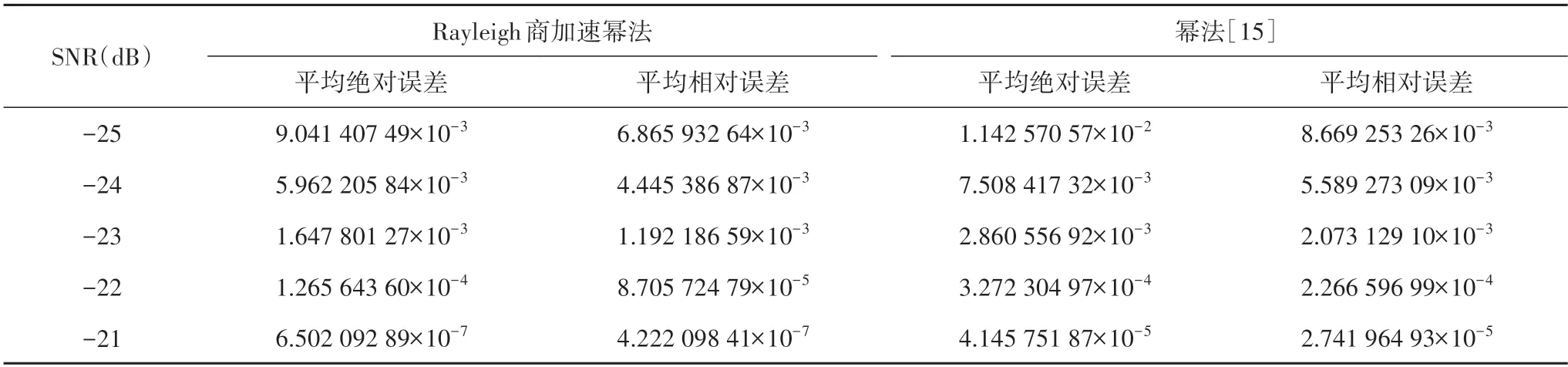
表4 Rayleigh商加速幂法计算感知判决量的平均误差Tab.4 Rayleigh quotient accelerated power method for the average calculating errors in test statistics

表5 给出了当N=3 200，M=64 时在不同目标虚警概率PFA条件下三次样条插值方法计算γMED的误差，其中真实门限值采用文献［16］中查表方法计算得到.由表5 的结果可知，在给定的一系列PFA值中，其对应的判决门限的最大绝对误差为2.014 490 63×10-3，最小绝对误差为2.548 672 64×10-5，最大相对误差为1.486 093 89×10-3，最小相对误差为1.958 776 01×10-5.通常绝对误差和相对误差在10-4或10-5数量级.由此可知，本文所提利用三次样条插值法计算判决门限产生的误差是极小的.

表5 三次样条插值法计算判决门限的误差Tab.5 Cubic spline interpolation algorithm for the calculation errors in decision thresholds

图3 给出了主用户信号为BPSK 信号时文献［9］和本文所提基于数值分析框架两种MED算法在PFA=0.1 时的性能对比曲线.仿真过程中设置M分别为32，64，128、256，信噪比从-30 dB 变化到-15 dB.Monte Carlo 仿真次数为5 000.这里经典的MED 算法采用eig 函数通过特征值分解方法计算精确的最大特征值，基于专用软件计算得到精确的判决门限.因此该方法的结果可以作为判断计算误差对感知性能影响大小的基准.采用本文所提方法时通过设置最大迭代次数K=500，误差界ε=10-4，然后利用Rayleigh商加速法计算λMED，并利用式（25）实时计算γMED.

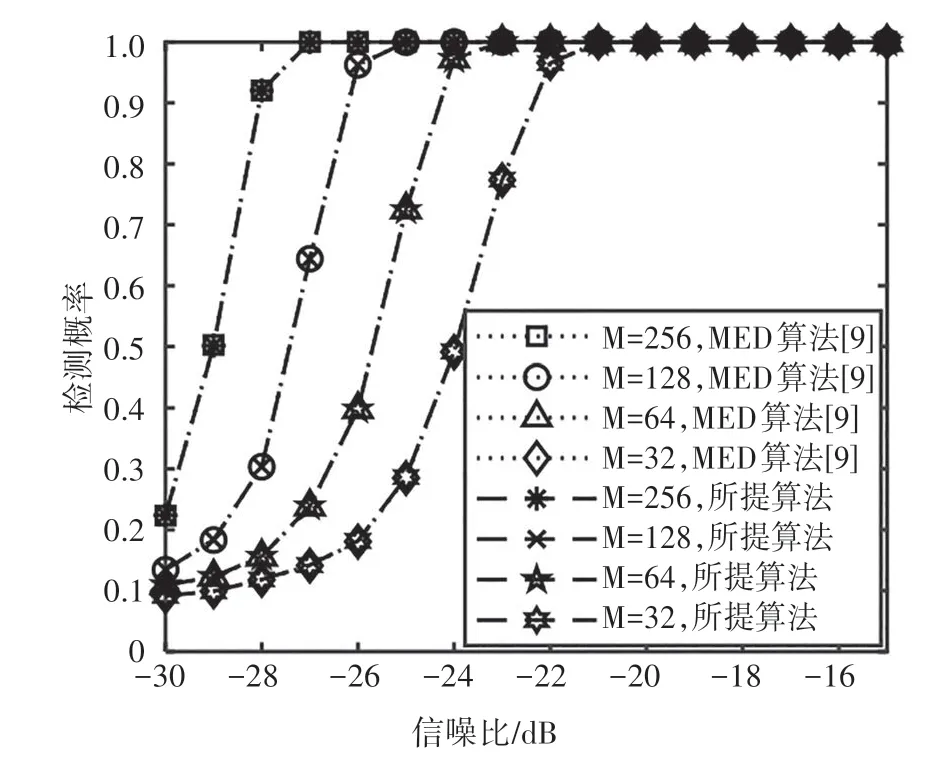
图3 经典MED算法与所提算法检测概率对比Fig.3 Comparison of the detection probabilities between the classical MED algorithm and the proposed algorithm

从图3 的仿真结果不难看到，本文所提方法的检测结果和文献［9］中经典计算方法获得的结果高度匹配.由此证明了本文所提基于数值分析理论的MED 算法产生了极为可靠的感知判决结果.这也表明本文所提利用Rayleigh 商加速法计算最大特征值，以及基于三次样条插值方法计算判决门限所引入的误差对感知判决结果带来的影响在实际应用中可以忽略.然而值得一提的是，本文所提方法比文献［9］中经典的MED 算法具有更低的计算复杂度和实现复杂度.与此同时，图4 给出了两种算法的实际虚警概率曲线的对比情况.这里文献［9］中经典MED算法采用专用软件计算精确判决门限.仿真结果清楚地表明，利用本文所提三次样条插值法产生的实际虚警概率和经典MED 算法产生的实际虚警概率同样高度匹配.这表明本文所提门限计算方法在具有极高的计算效率的同时，能够产生准确的判决门限，并获得可靠的虚警性能.

图4 经典MED算法和所提算法实际虚警概率对比Fig.4 Comparison of the actual false-alarm probabilities between the classical MED algorithm and the proposed one

为进一步评估本文所提MED 算法的性能.图5和图6 分别给出了信噪比和天线数目变化时算法的ROC 工作性能曲线.其中，图5 天线数目设置为64，图6信噪比设置为-28dB.图5的仿真结果表明，所提算法的检测性能随着信噪比的提高而提升.例如，当PFA=0.1 时，算法的检测概率在信噪比为-27 dB、-26 dB 和-25 dB 时分别为0.221 4、0.384 0、0.745 2，其检测概率随信噪比增大而明显增大.与此同时，图6的仿真结果表明，随着天线数目的增多，所提MED算法的检测性能相应提升.因此，在实际应用过程中可以通过增加天线的数目获得检测性能的增益.

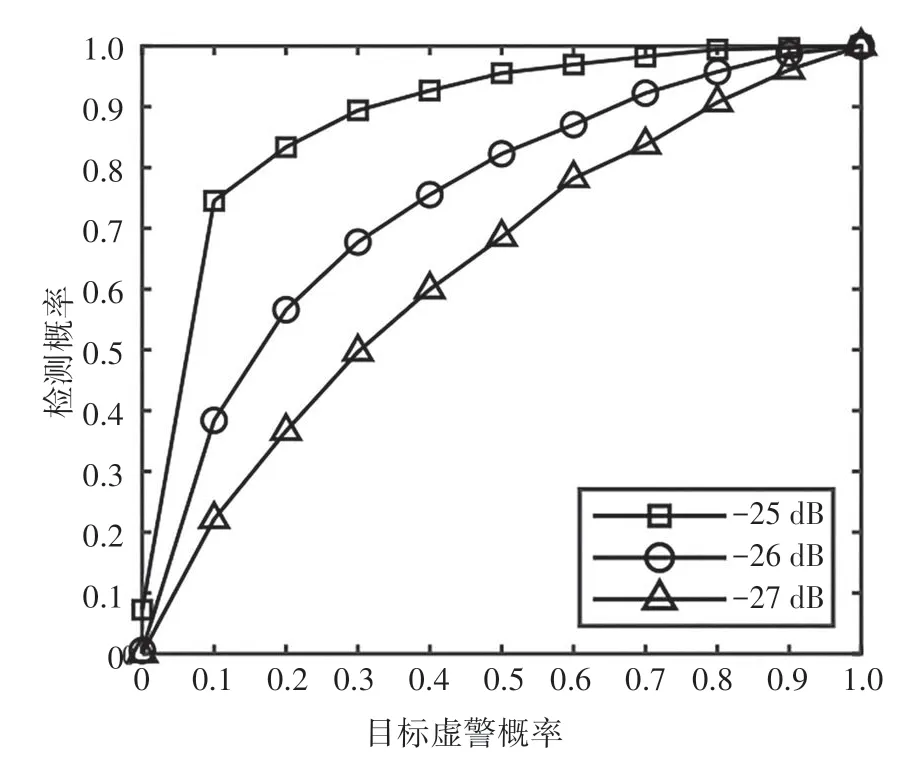
图5 信噪比变化时所提MED算法的ROC曲线Fig.5 ROC curves of the proposed algorithm when the signal-to-noise ratio changes

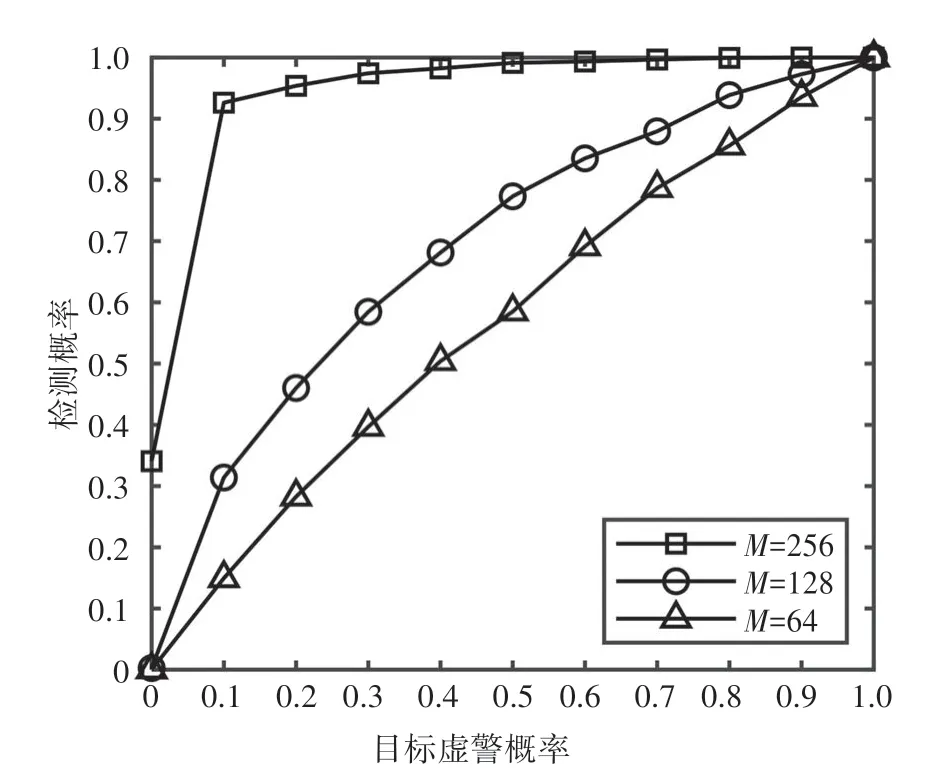
图6 天线数目变化时所提MED算法的ROC曲线Fig.6 ROC curves of the proposed algorithm when the number of antennas changes

4 结论

经典的MED 算法在5G、大规模协作等高维接收信号场景中面临着感知判决量和判决门限计算复杂度高以及难以实现的问题.为此，本文提出了一种基于数值分析理论的低复杂度MED 算法，该算法利用Rayleigh商加速幂法计算感知判决量，利用三次样条插值法计算感知判决门限.理论分析和实验仿真结果均表明，所提算法在高维信号感知条件下，在大大提升MED 算法计算效率的同时，能取得极为可靠的感知性能.本文所提出的基于数值分析理论的MED算法在现代认知无线通信中广泛存在的高维信号频谱感知场景方面具有广泛的应用前景.