例谈“以直代曲”思想在证明代数不等式中的应用

金 毅

(内蒙古自治区呼和浩特市第二中学 010000)

我们经常会见到一类条件不等式，给出有限个变量的范围或它们和的值，之后证明与这些变量有关的代数式的和的取值范围.

一种通常的表现形式是：

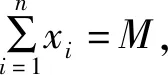
当然，等号或不等号的呈现形式也不唯一，以上仅作为一个常见表示展现给大家，目的是从形式上先做了解. 我们可以看到，很多解答中对这类问题都展现了非常高超的配凑变形技巧，这让我们不禁思考：对于这类问题在思考时的总体方向是什么？本文就将深入探究这类问题，将思考的过程予以展现，找出问题思考的总体方向，寻找隐藏在变形技巧后面的总体规律，并形成主要的解题思想——以直代曲.

1 “以直代曲”思想之割线放缩技巧

割线放缩是以直代曲思想的重要呈现，它的理论基础是函数的凸性. 关于函数的凸性，我们利用二阶导数判断，当f″(x)≤0在区间M上成立时，f(x)在区间M上为上凸函数；当f″(x)≥0在区间M上成立时，f(x)在区间M上为下凸函数.

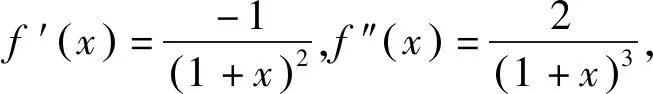
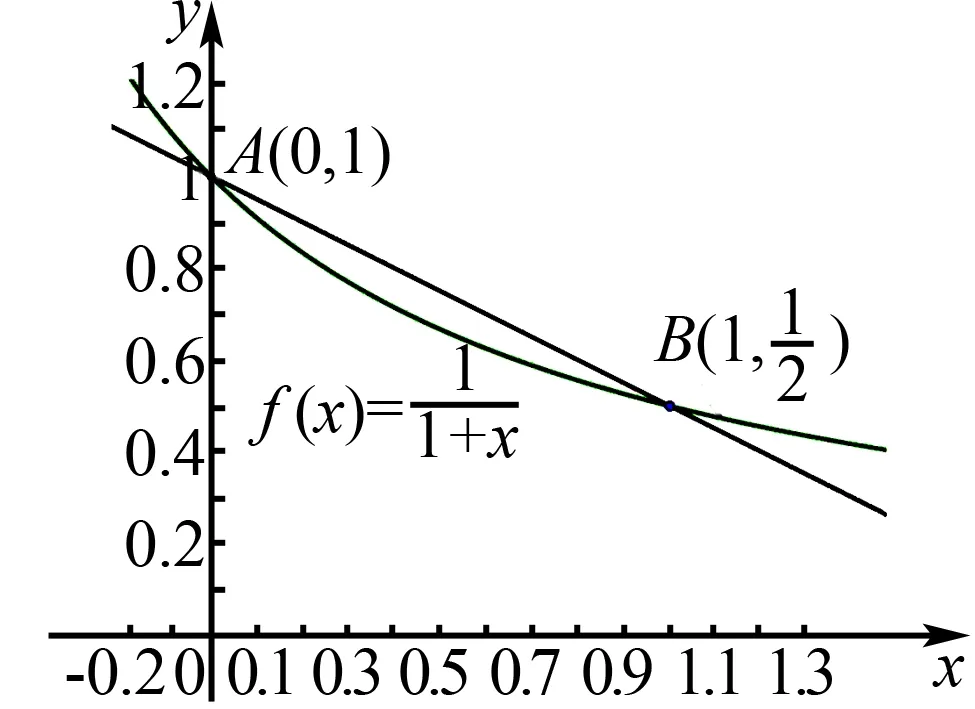
图1

这样，我们得到了在[0,1]上的不等关系

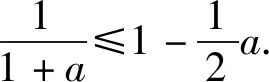
故原不等式成立，取等条件为a=b=c=d=1.

点评本题是利用割线放缩的一道典型例题，首先，整体的放缩方向是“往大放”，同时考虑到函数的凸性是“下凸”，于是想到“封口”处理. 从图1来看，直线和函数是“割线”关系，故名割线放缩. 事实上，根据刚才对例题的分析可以看到，函数的凸性是在放缩过程中必须要重点考虑的一个部分. 可以看到，割线放缩的关键是根据不等式的结构形式，找到要研究的函数，之后研究这个函数的凸性区间端点等非常重要的信息，之后确定直线的位置.

2 “以直代曲”思想之切线放缩技巧

通过刚才的分析，我们知道分析函数的凸性是极为重要的，这点不仅仅是应用在割线放缩中，切线放缩也至关重要. 同样，切线放缩也是“以直代曲”思想的重要呈现.

图2

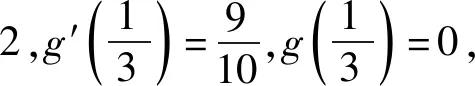
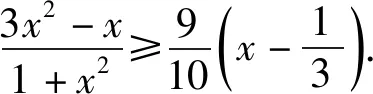
根据刚才的分析，[0,1]上的凸性不一致，所以我们要用作差配凑的方式严谨证明此不等式.

点评本题依据函数在取等条件时的凸性决定使用切线放缩. 本题的函数凸性不唯一，所以在证明时我们用了作差比较来严格证明. 例1的函数凸性唯一，所以我们使用图象说明即可. 切线放缩是一种更为常用的与函数凸性结合的方法，一般的步骤仍然是先分析函数凸性，根据不等号方向确定切线放缩的直线，同时，切点可以根据取等条件确定.

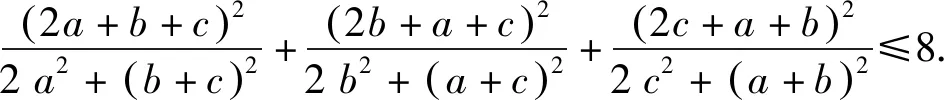
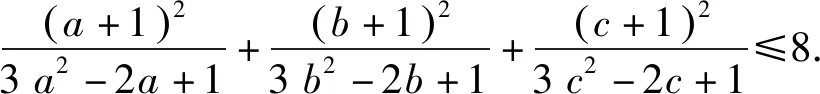
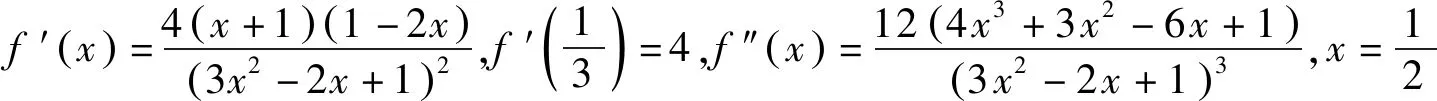
令h(x)=-36x3+15x2+2x-1，

h′(x)=-108x2+30x+2=(1-3x)(36x+2)，

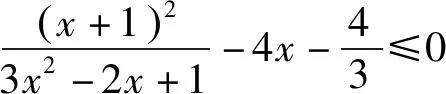
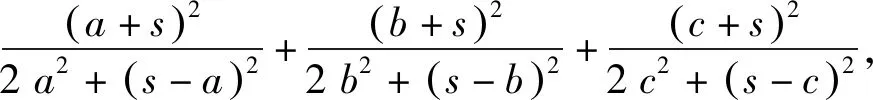
所以，令a+b+c=1，得到的是等价不等式，这样处理是合理的.

3 “以直代曲”思想之切割线放缩的综合应用

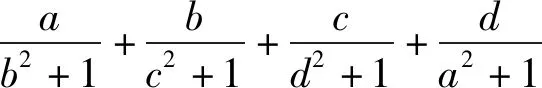
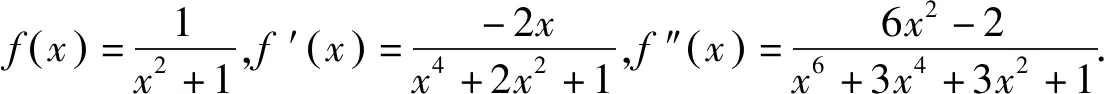
可以看出，在[0,2]上函数凹凸性不唯一，应该是先上凸再下凸. 结合要放缩的方向，我们总体上使用割线放缩. 但是，因为是先上凸后下凸，如果连接区间端点的话就会穿过图象，我们的考虑是从区间左端点向下凸部分引切线. 也就是说，我们用“切点”作为割线放缩“封口”的另一个端点.

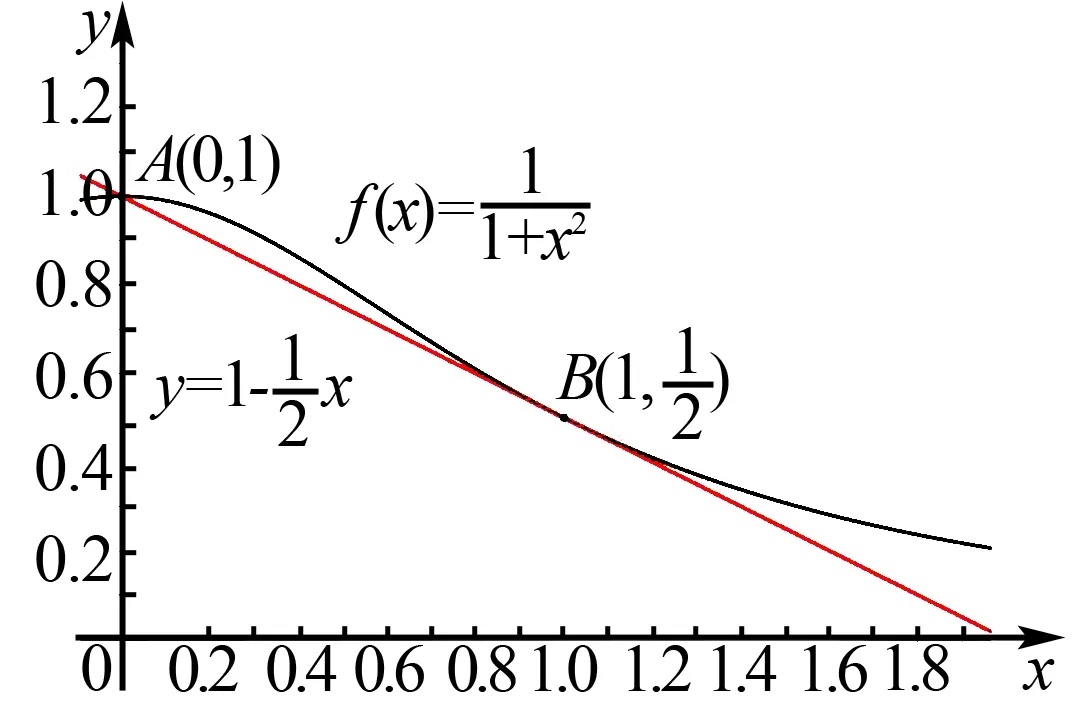
图3

点评从本题来看，虽然主体使用了割线放缩，但是其中的一个端点使用了切点，也就是说，本题综合使用了前面的两个“以直代曲”的思路. 事实上，在具体利用直线放缩不等式的时候，不是固定用切线或者是割线，而是一定要根据函数的凸性，“因地制宜”地选择解决问题的方法.

本文展示了“以直代曲”的具体思想来解决代数不等式问题，给出了每一个放缩时具体用的函数图象. 在实际做题中，函数的凸性分析是至关重要的. 一定要在具体的问题中灵活运用，用图形从直观形象的分析中尽快找到解决问题的思路.