驼峰车辆减速器制动噪声的复特征值分析
2022-11-03范家骅朱大鹏
范家骅, 朱大鹏
(兰州交通大学交通运输学院, 兰州 730070)
在中国的铁路系统中,驼峰进行列车解编组的能力直接影响到编组站接发车的工作效率,其中车辆减速器在驼峰设备中扮演了重要的角色。车列在驼峰峰顶解体,经过驼峰后将势能转化为动能,经过一系列的道岔以及减速顶或者车辆减速器对于速度的调整,从而使车体以适当的动能与同一方向的车列实现安全连挂。通常情况下,车辆下溜之后由于重力加速度的影响,速度会不断上升,经过车辆减速器时,位于车轮两侧的制动轨开口距离小于车轮厚度,车轮进入减速器挤开制动轨,制动轨会在机械结构的作用下对车轮进行钳夹,并通过摩擦力对车轮进行减速,从而使过高的车速降低至安全连挂速度。在车辆减速器对车轮进行制动的过程中,由于摩擦力的存在,迫使整个制动系统会产生不稳定的振动模态,进而向周围辐射高频尖叫噪声,人耳能感知到的声音频率范围为20~20 000 Hz,但是并不代表这些声音都能够被听到,这些高频尖叫噪声会对周围的工作和居住环境产生严重的物理性污染,对于人体的身心健康造成持续性的不良影响。一般人的语言声音频率主要集中在500~4 000 Hz,国际上通常将1000~20 000 Hz的振动噪声归为尖叫[1]。车辆减速器制动系统在工作时产生的声压级可达90~140 dB[2],过高的频率以及声压级会让人耳产生刺痛感,以及其他各方面的不良反应。
针对制动噪声产生机理的研究最早在20世纪30年代就已经出现[3-4],中国对于制动尖叫噪声的研究起步较晚,但是经过众多学者数十年的研究,已经对制动噪声的产生机理有了一定的认识。目前可以解释制动尖叫噪声的机理较多,如早期的摩擦力-相对滑动速度曲线的负斜率机理[5-6]、Sprag-slip机理[7]、热点理论[8]、模态耦合理论[9]、锤击理论[10]、转动盘双模态分离理论[11]等。陈光雄等[12-15]对踏面制动系统进行了初步的研究,采用了有限元复特征值分析方法,在踏面制动系统尖叫噪声方面取得了一定的成就。从现有的研究来看,模态耦合理论和锤击理论主要用于分析高频制动尖叫噪声,摩擦力-相对滑动速度曲线的负斜率机理更适合于分析速度较低时的摩擦颤振问题,而数值研究方法未能充分考虑制动系统的结构特征对于振动的影响,还需要继续进行研究[16]。近年来,模态耦合机理为大多数学者所认可,该理论认为,由于摩擦力的作用,制动系统中相邻振动频率之间的耦合作用很可能会使系统出现自激振动,不稳定振动的幅值会随时间进一步增大,进而迫使系统产生摩擦制动噪声,该理论能够反应系统的自然频率以及有外力耦合时的振动模态。研究制动尖叫噪声的方法主要分为试验法和有限元仿真法[17]。其中试验法虽然是最基本的研究方法,但是其结果具有一定的随机性,成本也较高,因此针对有限元模型的复特征值分析属于其中一种有效的分析方法[18]。
目前对于制动尖叫噪声的研究主要集中于盘式制动器和闸瓦制动系统等,鲜有针对驼峰车辆减速器制动尖叫噪声影响因素的分析[19]。为此,建立了车辆减速器主要部件的有限元模型,包括车辆走行轨、车轮以及车轮两侧的摩擦制动轨,基于复特征值分析法研究了制动轨与车轮间摩擦系数、制动轨对车轮的侧向作用力以及制动初速度对于制动尖叫噪声的影响。首先对现场的摩擦制动噪声进行了测试,利用快速傅里叶变换分析出噪声的主振频率。利用建立的制动系统有限元模型计算制动系统的固有频率,之后利用子空间投影法提取其复特征值和模态,通过实测结果与预测结果的误差对比验证模型的有效性。以期为降低驼峰工作环境噪声提供参考,保护工作人员的身心健康,同时为今后的车辆减速器降噪研究提供方向。
1 摩擦制动系统动力学原理
对驼峰车辆减速器制动系统进行适当的简化,以基本走行轨、车轮,以及车辆减速器进行制动作业时的两条制动轨作为研究对象,根据减速器的安装和工作状态建立动力学模型。首先对制动系统中各部件某一瞬时稳定运动的平衡状态进行分析,忽略了车轮转动的加速度对系统的影响,然后将耦合摩擦力的动态扰动应用于平衡状态,得到了系统的动力学方程,利用该方程可以进行复特征值分析。制动系统的运动方程可表示为
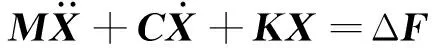
(1)
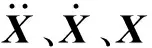
由于两接触面间存在摩擦力,因此M、C、K是非对称矩阵,C与摩擦力-速度曲线负斜率相关,这些特性是引起制动系统发生自激振动的重要诱因之一。
在轮轨接触问题中,认为接触面的摩擦力可能是产生振动的主要原因[20]。因此力向量ΔF可以是两接触区域的接触刚度和位移的函数,可表示为
ΔF=KfX
(2)
式(2)中:Kf为非对称摩擦刚度矩阵。
将式(2)代入式(1)得
(3)
由此得到对应的特征方程为
[Mλ2+Cλ+(K-Kf)]φ=0
(4)
式(4)中:λ为特征根;φ为特征向量。
对方程进行求解,其通解为
(5)
式(5)中:i为阶数;λi=αi+iωi为第i阶特征根;αi为第i阶特征根的实部;ωi为第i阶特征根的虚部;t为时间;φi为第i阶特征向量。
对于一个制动系统的三维有限元模型,其中的每一个节点都有3个正交的平移自由度,需要利用两接触面间的库仑摩擦力将法向自由度与切向的两个自由度耦合起来,从而得到非对称的有限元矩阵。利用得到的矩阵进行求解,可通过解得的复特征值对系统的稳定性进行判断。每一个节点自由度都有对应的特征值和特征向量,若复特征值实部为正,意味着任意微小扰动都会使节点位移成倍放大,经过累积就会使整个振动系统失稳,从而激发出制动尖叫噪声。复特征值实部的正值越大,对应的振动模态出现失稳的可能性就会越大[21]。因此解决复特征值问题有助于预测系统发生制动尖叫的倾向。
2 车辆减速器制动系统有限元模型
典型的目的制动位车辆减速器结构如图1所示,以T·JK(Y)2系列某目的制动位减速器为参考对象,铁路货车车轮采用CL60辗钢整体车轮,标准外径R=420 mm,内径R1=370 mm,车轮厚度δ=135 mm,弹性模量E=2.06×1011Pa,泊松比v=0.3,密度ρ=7.8×103kg/m3。两侧制动轨由60 kg/m钢轨改制而成,材质为U71Mn,弹性模量E=2.06×1011Pa,泊松比v=0.3,密度ρ=7.85×103kg/m3。该型钢轨含碳、硅、锰量较高,可焊性差,因此喇叭口采用直接加工的方式制成,制动轨的有效长度随减速器节数n的变化而变化,通常n∈{4,5,6,7},选取n=4的情况进行研究,减速器有效制动长度L=4.8 m。制动时,内、外制动轨上侧面至基本轨轨顶的高度分别为hinside=80 mm、houtside=72 mm。根据车辆减速器制动时,车轮与制动轨的实际位置关系和工作状态,建立图2所示的制动系统实体模型。为了便于建模,除车轮和制动轨外,安装在车轴上的所有部件以及制动轨的所有支撑部件都被忽略。车轮和基本走行轨采用C3D8R六面体单元进行网格划分,数量为161 450个;两侧制动轨采用C3D10四面体单元进行网格划分,数量为395 510个,均采用增强型沙漏控制。边界约束为:对基本走行轨进行刚体约束,并限制其6个自由度上的位移和转动;限制制动轨20个安装螺栓孔在圆柱坐标系下的竖向、纵向位移,但不约束横向位移;限制车轮轮毂孔在x、y、z方向上的平移,但不约束转动;编辑inp文件关键字定义车轮转动初速度;缸压通过制动钳等机械结构作用在制动轨螺栓孔上。

图1 车辆减速器结构Fig.1 Structure of vehicle reducer

图2 车辆减速器制动系统有限元模型Fig.2 Finite element model of braking system of car retarder
3 摩擦制动噪声测试
3.1 测试方案
某编组站驼峰一部位减速器共有2线束,二部位减速器共有6线束,三部位减速器共有30股道,以T·JK(Y)2系列某目的制动位减速器作为研究原型,因此选取三部位的一台减速器进行测试。采用B&K4966型自由场传声器,采样频率范围为5~20 000 Hz,预极化设计,声音通过带前置放大器的传声器进入数据采集前端,经过系统的分析之后在计算机中显示和输出。由于是在室外开阔环境中进行测试,为了尽可能避免车体以及地面反射声波的影响,传声器距离地面1.2 m,距离减速器外侧制动轨1 m。
3.2 测试结果
在减速器对经过车辆进行制动的过程中采集11 s的有效制动噪声,采集现场的环境噪声数据并在MATLAB中对制动噪声进行分析,得到时域分布如图3所示,之后采用快速傅里叶变换提取噪声的频域分布如图4所示。可以看出,有一部分小于100 Hz的频率存在,这可能是环境中存在的背景噪声引起的。当两个声压级相差比较大的声音同时作用时,总声压级升高的幅度几乎可以忽略,因此背景噪声对于尖叫噪声声压级的影响微乎其微,可以主要对高频高声压级进行频域分析。测试中提取到的主要振动频率为1 957.04、2 280.54、2 509.71、3 550.26、4 337.35、4 482.37、5 522.25、7 756.74、7 955.82、8 727.29 Hz。
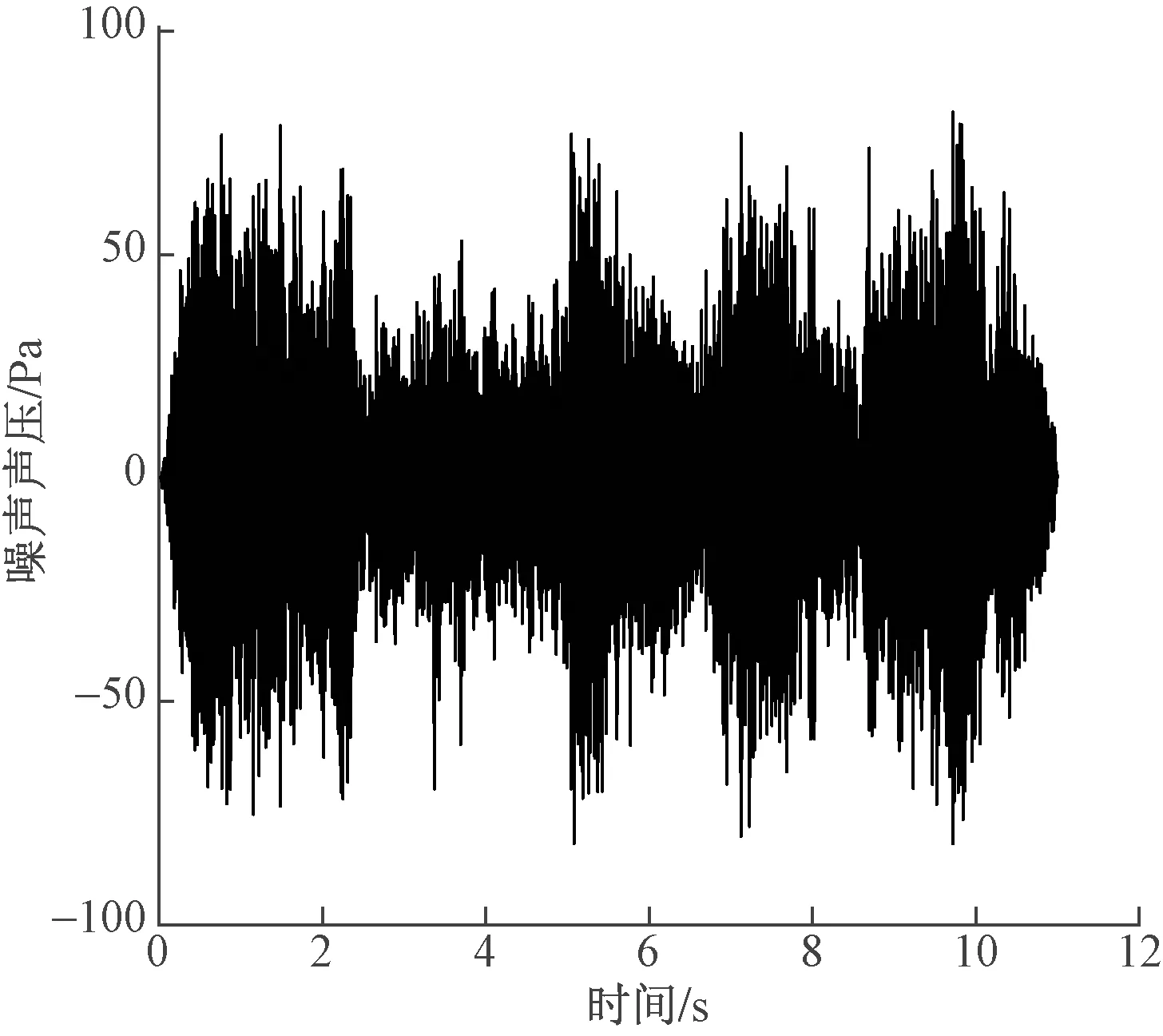
图3 噪声信号时域分布Fig.3 Time domain distribution of noise signal
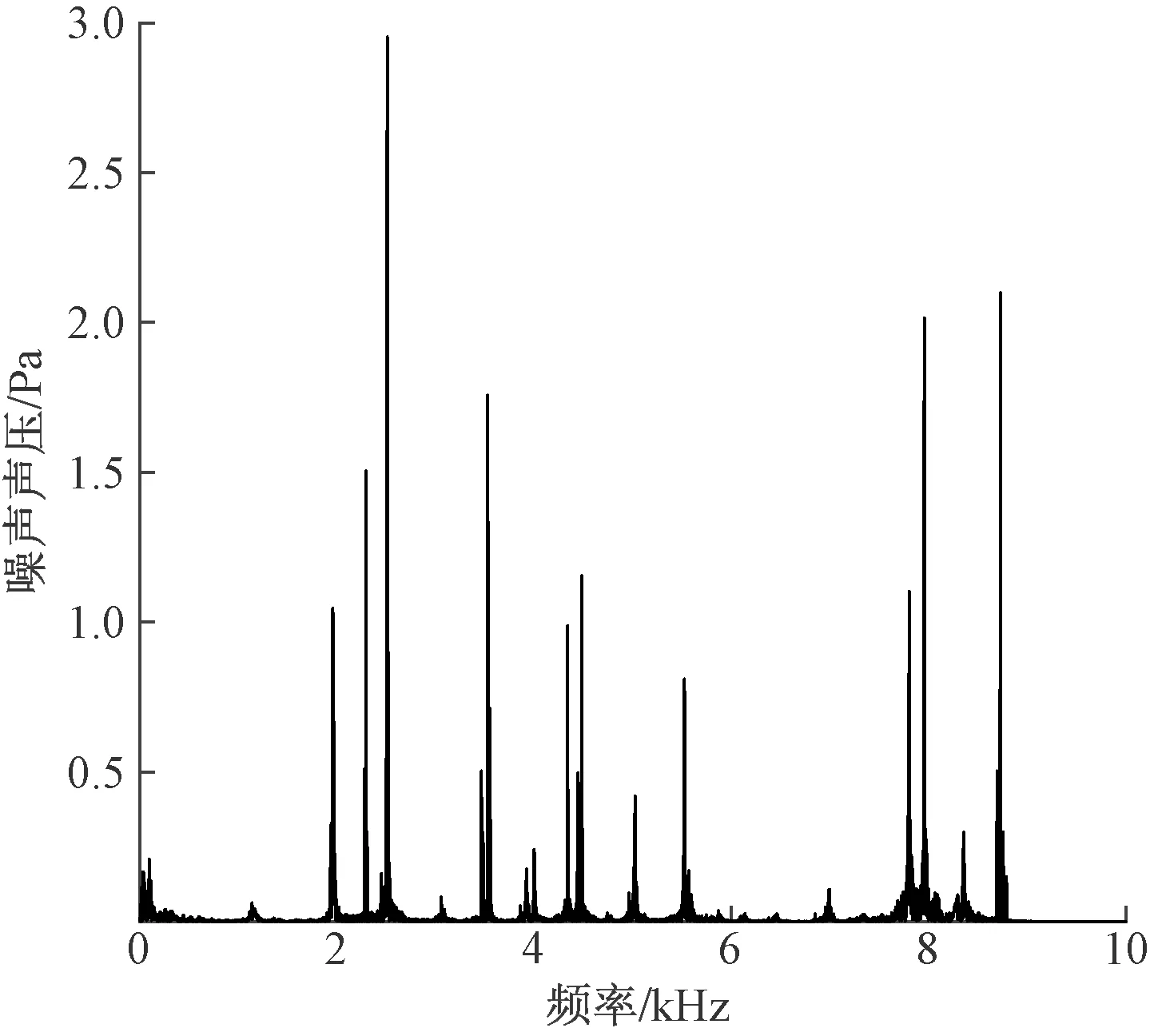
图4 噪声信号频域分布Fig.4 Frequency domain distribution of noise signal
3.3 理论预测结果
对于建立的有限元初始分析模型,选取摩擦系数μ=0.13,车轮转动初速度ω=10 rad/s,制动轨对车轮的侧压力F=120 kN,进行复特征值分析,得到图5(c)所示的结果,其中不稳定模态约有20个,将实测噪声中具有代表性的振动频率与预测结果中的主要不稳定模态进行对比,得到表1。
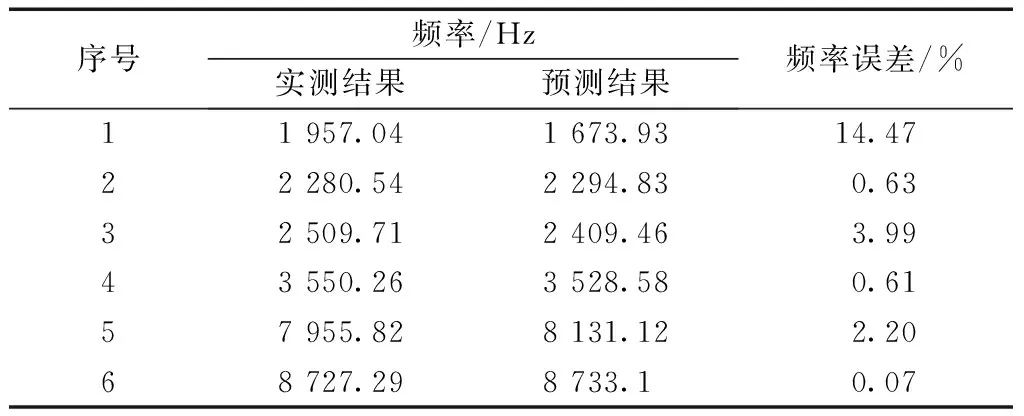
表1 理论预测频率误差Table 1 Relative error of theoretical prediction frequency
4 有限元模型结果分析
4.1 摩擦系数对制动尖叫噪声的影响
为了研究制动轨轨面与车轮外侧接触时的摩擦系数对于制动尖叫噪声的影响,分别定义了摩擦系数μ为0.07、0.1、0.13、0.17时的有限元模型,其他边界条件及载荷保持不变。车轮转动初速度为ω=10 rad/s,车轮滚动圆半径R=420 mm,因此,线速度v=4.2 m/s;制动轨对车轮的侧压力F=120 kN。通过复特征值分析,得到了不同摩擦系数时制动系统不稳定模态在频域上的分布,如图5所示。可以看出,当摩擦系数较小时,基本没有出现高频不稳定振动模态,但随着摩擦系数的增大,出现的不稳定模态在增多,集中于2~4、8~10 kHz的不稳定模态逐渐扩展至全域,相应地高频模态数量增长也较为可观。这表明车辆减速器制动系统中,摩擦系数越大,可能产生的不稳定模态越多,系统辐射高频尖叫噪声的倾向也越大。
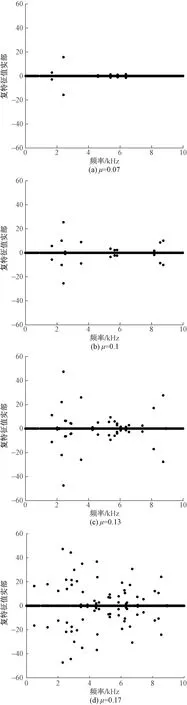
图5 摩擦系数对制动尖叫噪声的影响Fig.5 Effect of friction coefficient on braking squeal noise
为了进一步研究制动系统随摩擦系数增加而出现的模态耦合现象,图6给出了制动系统第664、第665阶频率随摩擦系数的变化情况。由图6(a)可知,摩擦系数μ=0.07、0.1时,第664、第665阶频率没有耦合;当μ=0.13、0.17时,第664、第665阶频率发生耦合,此时的振动频率分别为8 131.12、8 136.17 Hz,同时系统出现了不稳定模态,如图6(b)所示。
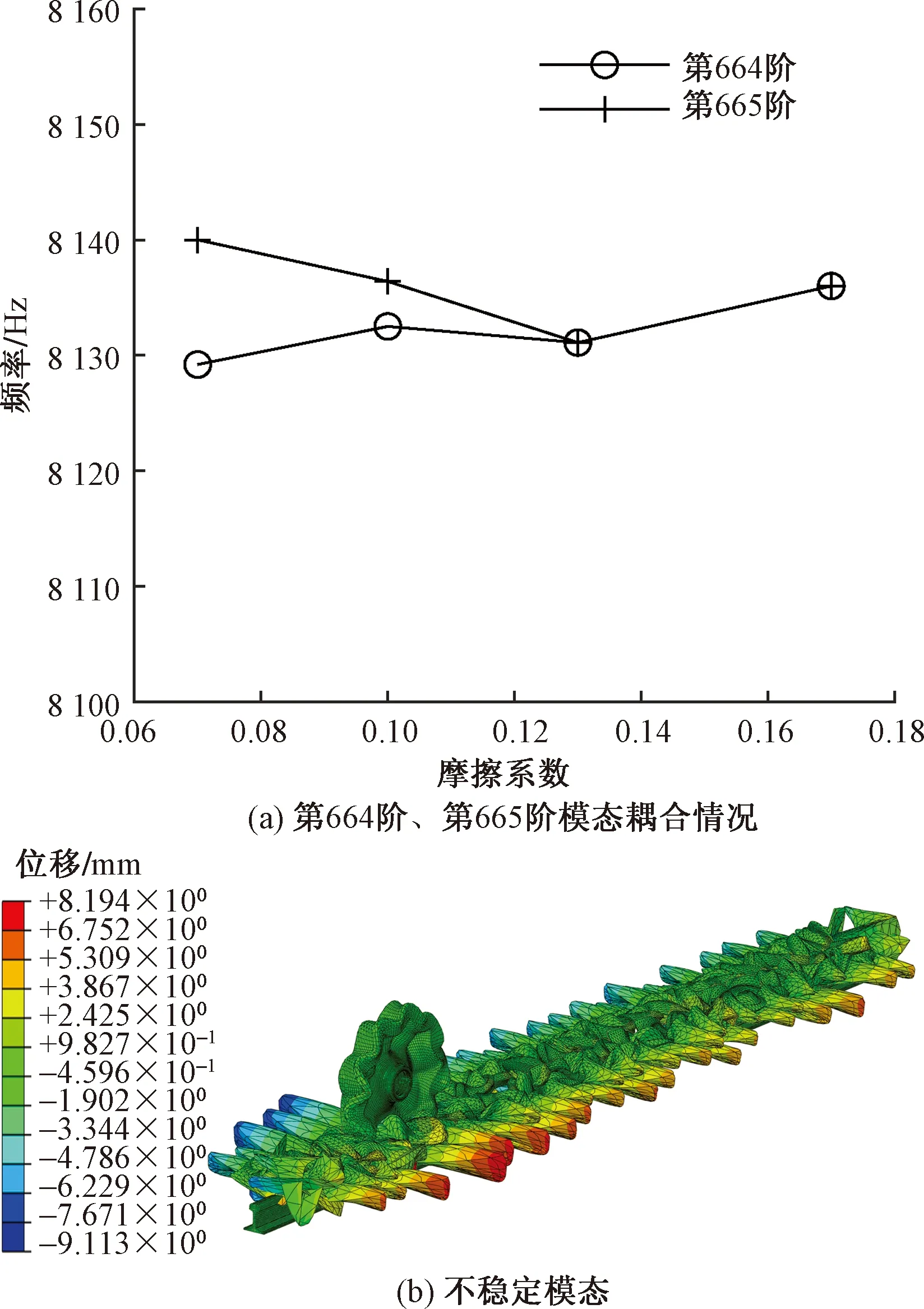
图6 模态耦合现象Fig.6 Phenomenon of modal coupling
4.2 制动轨作用力对制动尖叫噪声的影响
保持摩擦系数μ=0.13,车轮转动初速度ω=10 rad/s,改变制动轨对车轮的侧压力载荷,分别建立F为50、190、260 kN时的有限元模型。对于非重力式减速器来说,制动轨侧压力与缸压以及机械杠杆比直接相关,对于重力式减速器来说,除了上述两个参数,制动轨侧压力还与车辆轴重有关,通过相应的公式对轴重约为5 t的空车以及25 t的重车进行计算,得到重力式减速器制动轨对车轮的侧压力范围大致为50~260 kN。进行复特征值分析,得到不稳定模态在频域上的分布如图7所示。与图5(c)对比分析之后可以发现,随着侧压力的不断增加,复特征值实部大于0的不稳定模态从15个增加到30个,同时实部值的绝对值也相应增大,6~10 kHz的高频模态也相应增多。这表明制动轨侧压力对制动系统发出高频尖叫噪声的倾向也有一定的影响。
为了进一步研究制动系统随制动轨侧向力增加而出现的模态耦合现象,图8给出了制动系统第626、627阶频率随制动轨侧向力的变化情况。由图8(a)可知,当F=50 kN、120 kN时,第626、627阶频率没有耦合;当F=190 kN、260 kN时,第626、627阶频率发生耦合,此时的振动频率分别为7 698.40 Hz、7 698.60 Hz,同时系统出现了不稳定模态,如图8(b)所示。
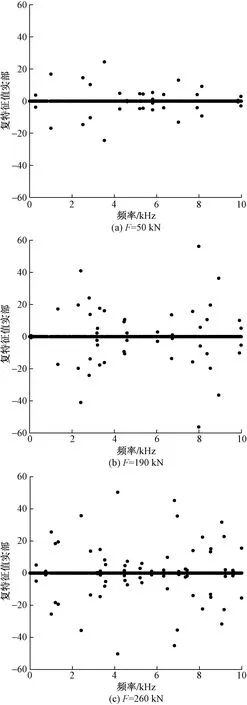
图7 制动轨作用力对制动尖叫噪声的影响Fig.7 Influence of braking rail force on braking squeal noise
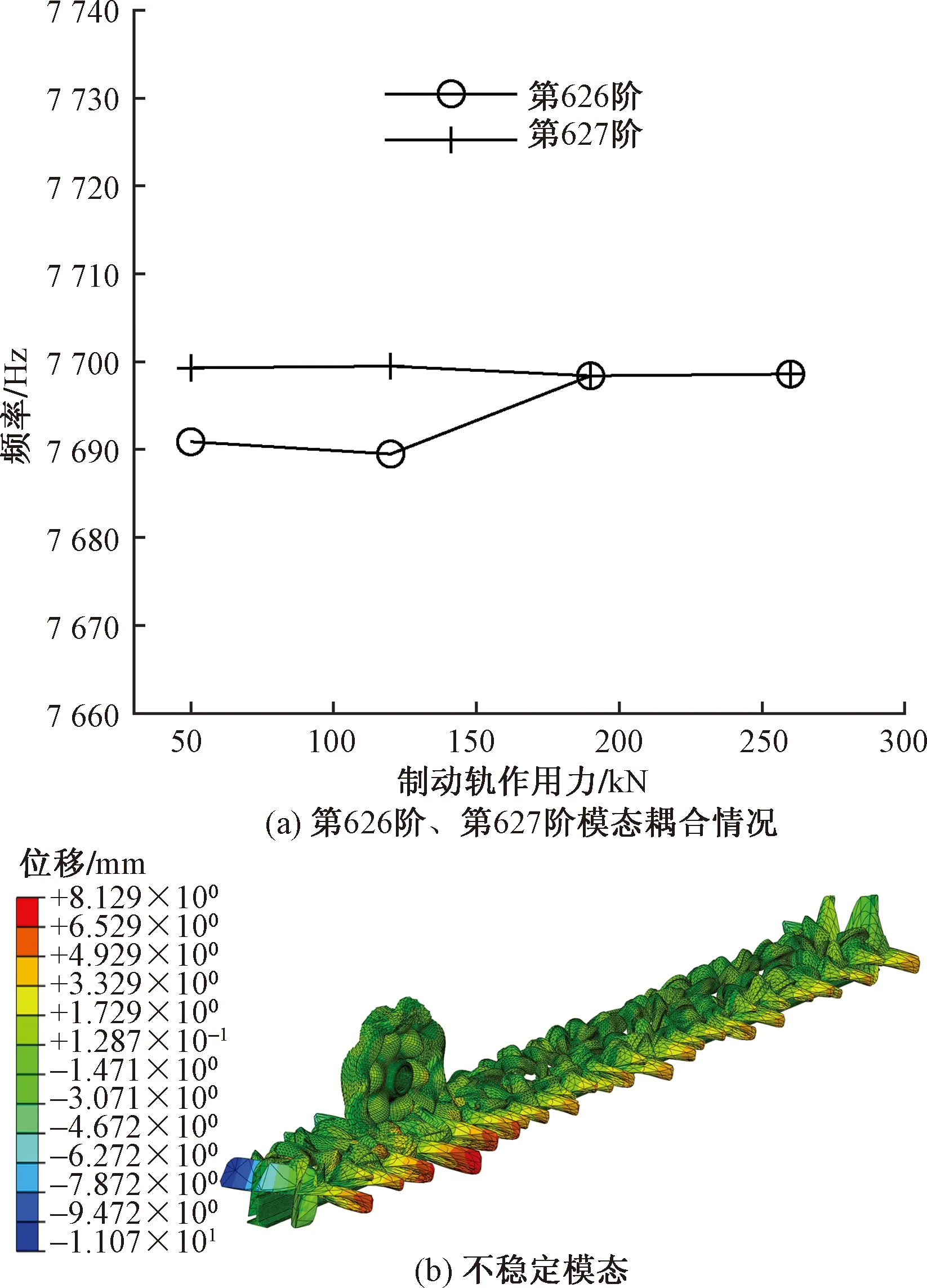
图8 模态耦合现象Fig.8 Phenomenon of modal coupling
4.3 车轮转速对制动尖叫噪声的影响
保持摩擦系数μ=0.13,制动轨对车轮的侧压力载荷F=120 kN,改变车轮转动初速度,分别建立ω=5、15 rad/s时的有限元模型,对应的线速度分别为v=2.1、6.3 m/s。进行复特征值分析,得到不稳定模态在频域上的分布如图9所示。与图5(c)对比分析之后可以发现,3种车轮转速下的不稳定模态数量及分布极为相似,数值上仅有细微的差别。出现这种情况可能是因为摩擦力-相对滑动速度曲线中2~6 m/s的速度范围内,曲线斜率较为平缓,速度变化对于摩擦系数变化的贡献较小,导致接触面的摩擦系数变化较小,从而使得不稳定模态变化不大,这还需要进一步分析研究。
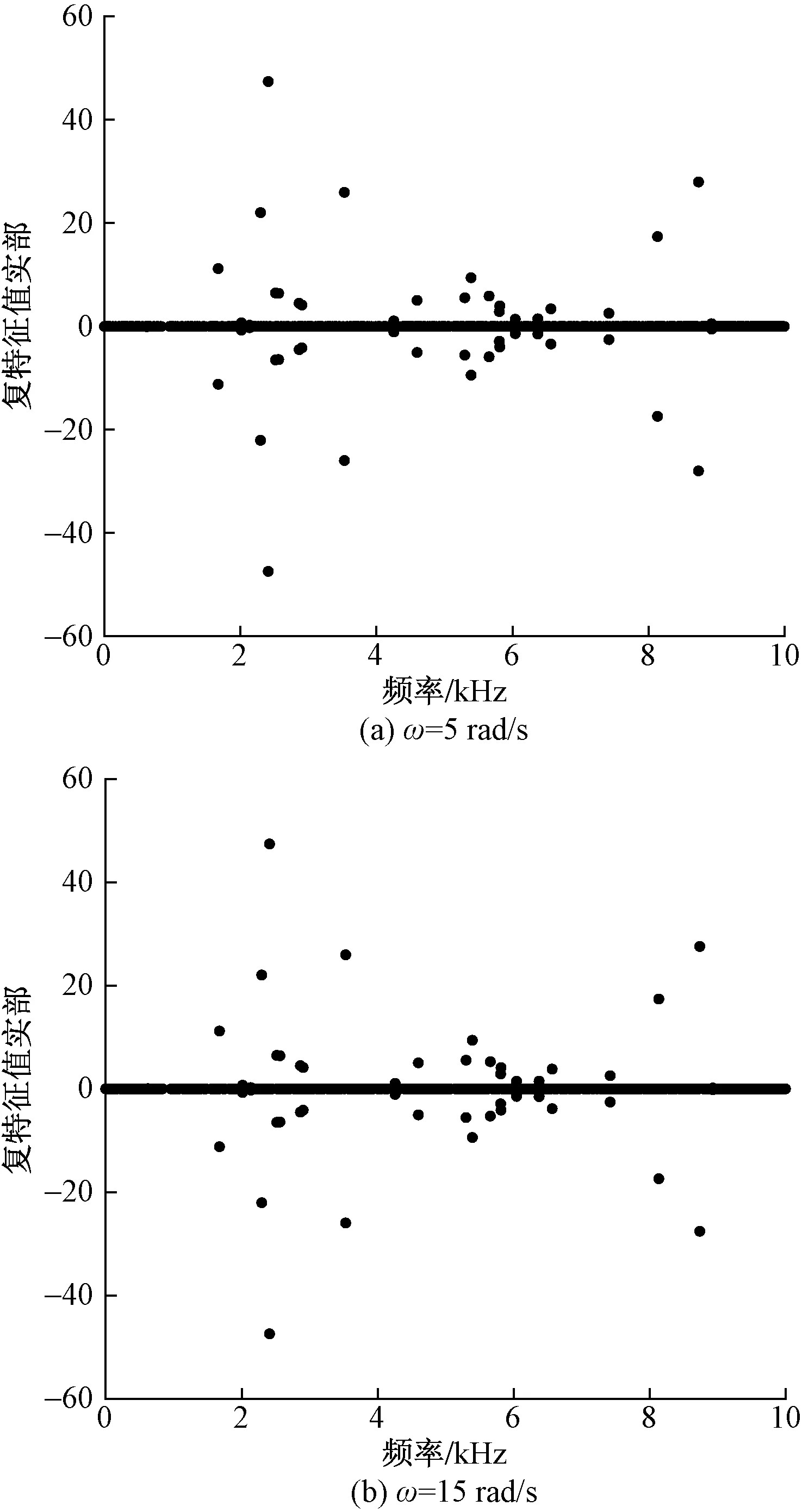
图9 车轮转速对制动尖叫噪声的影响Fig.9 Influence of wheel speed on brake squeal noise
5 结论
(1)驼峰车辆减速器的制动力来源于摩擦力,摩擦力对于制动系统产生不稳定模态的倾向具有重要影响。
(2)摩擦系数增大会导致系统产生更多的不稳定模态,为降低系统辐射高频尖叫噪声的倾向可以考虑采用其他复合材料制作制动轨,在一定程度上减小摩擦系数。
(3)较大的作用力会使车轮与制动轨之间的振动耦合更为明显。
(4)车轮转速在2~6 m/s的速度区间时对振动系统的影响较小,结合以上结论,可以考虑增加制动轨的有效制动长度,用低能高加长距离的方式减弱尖叫噪声发生的可能性。
