降雨入渗对锚杆加固多级边坡稳定性影响分析

2022-11-03周粲铭董旭光李峥马子涵

科学技术与工程 2022年28期

周粲铭，董旭光，李峥，马子涵

(宁夏大学土木与水利工程学院, 银川 750021)

降雨是导致土坡发生相对滑移及工程事故频繁发生的重要因素[1]。其中公路边坡与人们的交通出行密切相关，降雨引发的边坡突发性病害影响交通正常运行，并危及行车安全。近年来，频繁出现的极端暴雨天气导致的滑坡事件使人们的生命财产受到巨大损失。据统计，自20世纪以来，中国由强降雨直接触发的大型灾害性边坡失稳超过50%[2]。地质灾害调查也表明，降雨是西北黄土高原边坡失稳的重要因素[3]。因此,进行降雨入渗下黄土边坡稳定性研究具有重要的实际意义与价值。随着由降雨引发的滑坡事故的不断发生，降雨对边坡稳定性影响受到了中外学者的广泛关注。

Liu等[4]基于水-气两相流模型，通过降雨原型实验，研究了气流对土质边坡稳定性的影响。孙自立等[5-6]基于最小势能法，得到了降雨作用下边坡渗流场的解析解。郑开欢等[7]通过数值模拟，研究了长时间暴雨对边坡稳定性的影响。徐全等[8]对降雨作用下的土质边坡进行了固-流耦合分析及不耦合分析，研究了饱和渗透系数及降雨强度对边坡安全系数及滑面位置的影响。邵珠山等[9]基于Green-Ampt入渗模型，考虑了降雨强度及降雨时长的影响，推导了不同降雨工况下边坡安全系数的关系式。曾玲等[10]通过数值模拟的方法对边坡暂态饱和区的形态与特征进行研究，研究结果表明：不同土层结构与降雨工况均会对边坡暂态饱和区的分布范围产生影响。缪海宾等[11]通过基底黄土孔隙水压力消散试验，并基于极限平衡法和孔隙水压力消散规律，提出了黄土基底排土场动态稳定系数计算方法。廖军等[12]建立路堤填筑前后计算模型，对长期降雨作用下路堤填筑前后的稳定性进行分析。杜忠原等[13]利用PLAXIS有限元软件，分析了不同降雨强度下边坡孔隙水压力的变化规律、边坡的破坏趋势、以及边坡安全系数的变化。然而，诸多学者的研究成果中，以多级边坡为对象，分析降雨作用对锚杆支护边坡稳定性的影响较少。

基于此，利用Geo-studio有限元分析软件，建立考虑降雨入渗对锚杆支护结构下多级边坡稳定性分析的二维数值模型。研究不同降雨工况下边坡剪应力、孔隙水压力、安全系数、坡面位移、锚杆轴力的变化规律。为锚杆支护多级边坡稳定性分析及灾害防治提供理论支持。

1 理论基础

1.1 非饱和土体强度计算原理

Fredlund等[14]基于Mohr-Coulomb强度理论提出的非饱和土体抗剪强度，该强度常用于降雨入渗工况对土体强度的评价表达式为

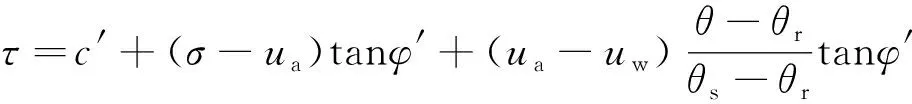
(1)

式(1)中：τ为非饱和土抗剪强度；c′为非饱和土体的有效黏聚力；σ为非饱和土体上的总应力；ua为孔隙气压力;uw为孔隙水压力；φ′为土体内摩擦角；(ua-uw)为基质吸力；(σ-ua)为净法向应力；θ为土体体积含水量；θs为土体饱和体积含水量；θr为土体残余体积含水量。

天然状况下，位于地下水位以下的边坡土体为饱和土，其渗透系数为定值。而位于地下水位以上的土体为非饱和土。在非饱和土渗流过程中，土体的渗透系数受基质吸力及体积含水量的变化而变化。体积含水率与基质吸力的关系曲线称为土水特征曲线，可以通过室外试验来确定，但试验操作周期长、费用高。因此一般通过经验公式来得出，常用的经验模型有VG(Van Genuchten)模型及Fredlund Xing模型，采用VG经验模型函数拟合确定土体土水特征曲线，再根据土水特征曲线及饱和渗透系数进一步确定土体的渗透系数函数。在Geo-studio的SIGMA/W子模块中设定相应的VG控制方程的参数来确定多级锚杆加固边坡的渗透系数函数，其表达式为

(2)

(3)

式中：θw为体积含水率；ψ为基质吸力；Kw为渗透系数；Ks为饱和渗透系数；α、m、n为土-水特征曲线形状参数。

1.2 渗流理论

边坡的渗流过程符合达西定律，假设锚杆加固多级边坡同样符合普通边坡的渗流过程，故根据质量守恒原理，可得本文模型中降雨入渗时的二维渗流基本方程表达式为

(4)

式(4)中：Kx为水平方向的渗透系数；Ky为竖直方向的渗透系数；H为总水头；mw为比水容重；γw为水的重度；Q为汇源量；t为时间。

1.3 极限平衡法

无论单级或多级边坡,极限平衡法是分析边坡稳定性问题的基础理论，在边坡稳定性分析的工程案例中广泛运用[15-16]。考虑到Morgenstern-Price法能满足严格的极限平衡条件，故利用该理论对边坡稳定性进行计算。

2 降雨入渗下锚杆加固多级边坡的计算模型

降雨入渗条件下锚杆加固多级边坡的应力场、渗流场和稳定性变化过程极其复杂，Geo-studio有限元分析软件可进行边坡流固耦合及稳定性分析。采用Geo-studio软件的SLOPE/W子模块分析边坡稳定性，该模块能运用极限平衡理论对不同种类土体、复杂地层、孔隙水压力状况和不同加载方式下对边坡稳定性进行分析。选用Morgenstern-Price法分析不同工况下边坡的稳定性。

2.1 工程概况

宁夏六盘山公路路堑某三级边坡，坡高为26 m，沿边坡倾斜方向长度60 m，分3级，平台宽度为3 m，坡率为1∶1.33。边坡的地下水位为左侧上游水位标高18 m，右侧下游标高11 m。土体分2层，下部分为粉质黏土，上部分为黄土。用锚杆对该边坡进行加固，锚杆采用直径为25 mm的HRB400钢筋，水平间距为2.5 m，锚固体直径为200 mm，与水平面的夹角为15°，土体力学参数如表1 所示，钢筋力学参数与锚杆设计参数分别如表2、表3所示。土水特征曲线与渗透系数曲线分别如图1、图2所示。

2.2 模型建立

利用Geo-studio建立二维有限元计算模型如图3 所示。土体视为各向同性的均匀土质，土体单元采用四边形实体单元，锚杆采用杆单元。土体本构关系采用理想的摩尔库伦弹塑性模型。位移边界条件：模型底部水平及竖直方向的位移约束，两侧进行水平方向约束。流体边界条件：在边坡水平面及斜坡面施加单位流量边界，其余表面设置为不透水边界。为了更好地观察降雨入渗规律及锚杆加固边坡的应力、位移和稳定性变化，在边坡表面设置监测点。首先利用Geo-studio中SIGMA/W原位分析模块，对有限元计算模型进行应力重分布并平衡初始地应力；其次将得到的稳态应力场导入 SIGMA/W 耦合应力、孔隙水压力模块进行渗流-应力耦合分析，在此模块中添加边界条件并进行计算，得到瞬态渗流场和应力场，并将其导入SLOPE/W模块，得到随时间变化的边坡安全系数及滑移面。图3中，A～F为监测点，红色区为粉质黏土，黄色区为黄土。

表1 土体力学参数

表2 钢筋力学参数

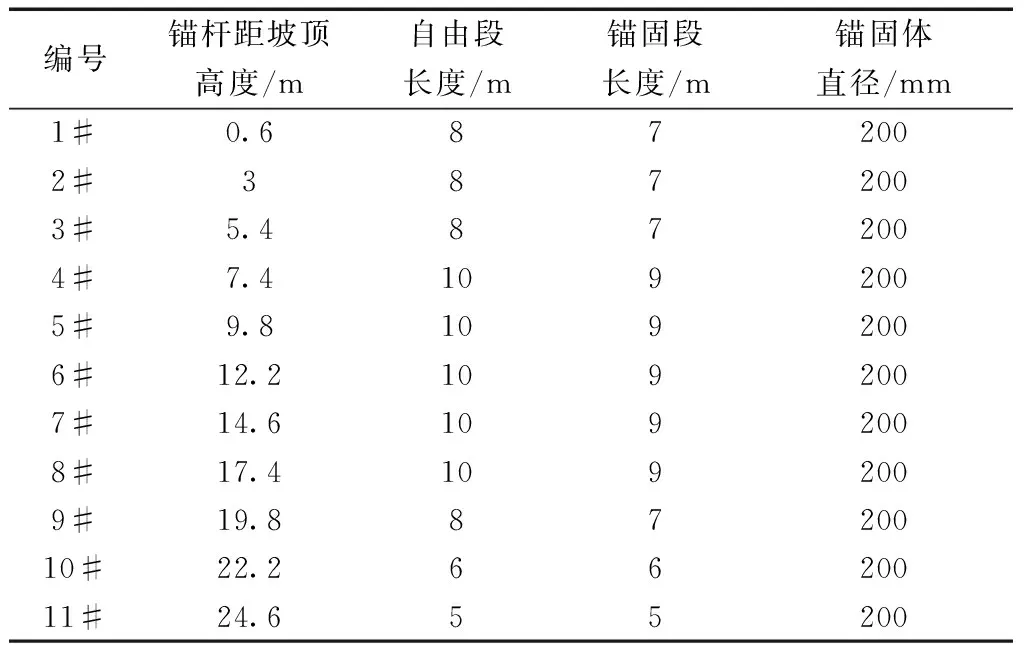
表3 锚杆设计参数

图1 土水特征曲线Fig.1 Curves of soil water characteristics

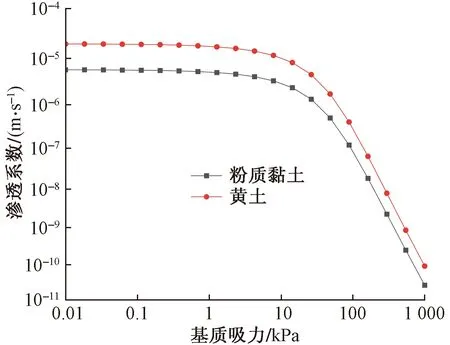
图2 渗透系数曲线Fig.2 Curves of permeability function

图3 二维有限元计算模型Fig.3 2D finite element calculation model

2.3 计算方案

中国气象局将降雨强度分为6类：小雨、中雨、大雨、暴雨、大暴雨、特大暴雨。采用了4种降雨强度，分别为中雨20 mm/d、大雨40 mm/d、暴雨 80 mm/d、大暴雨240 mm/d，分析不同降雨时间条件下，坡体孔隙水压力、安全系数、坡面位移和锚杆轴力变化情况。降雨时长设置为连续的5 d，降雨结束后，考虑停雨5 d的工况。

3 结果与分析

3.1 降雨入渗对孔隙水压力的影响

图4 初始状态下边坡孔隙水压力分布Fig.4 Distribution of pore water pressure of slope under initial state

初始状态下，边坡孔隙水压力的分布如图4所示。可以看出，在不添加降雨流量边界条件时，边坡的地下水位线是平滑的折线，且孔隙水压力等值线平行于地下水位线。降雨24 h后，不同雨强下边坡孔隙水压力分布如图5所示。可以看出，位于边坡表层土体的孔隙水压力受降雨的影响最大，这是由于表层坡体最先对降雨做出响应，且雨水的入渗深度有限，因此边坡表层含水率的增大幅度大于边坡深层土体。根据土水特征曲线可知，土体的基质吸力大小与体积含水率呈负相关，因此雨强越大，位于坡顶土体的含水率越大、基质吸力越小。可见随着雨强增加，边坡表层土体的孔隙水压力在相同降雨持时下增大越快。当雨强为240 mm/d时，土体基质吸力降为0，即土体孔隙水压力为0，说明当雨强度达到一定值时,边坡表面会出现短暂性积水状态，主要原因是雨强大于土体的渗透系数。

图5 不同雨强降雨24 h后边坡孔隙水压力分布Fig.5 Pore water pressure distribution diagram of slope after 24 hours for different rainfall intensity

3.2 降雨入渗对边坡位移的影响

锚杆加固边坡的特征点水平位移与降雨持时关系如图6所示。当雨强为20、40 mm/d时，降雨初期，边坡上游水位高于下游，土中水在重力作用下由上游向下游移动，上游地下水位降低，土体脱水孔隙比减小发生收缩，特征点B、D、E产生指向坡内的水平位移。随着降雨持续进行，边坡水平位移增加，主要原因是降雨持续入渗对边坡产生渗透力，改变了边坡原位状态的应力场，土体发生变形；降雨持时越大，边坡位移越大。雨停后，作用于土体的渗透力迅速减小，土体位移基本不变。当雨强为80、240 mm/d时，降雨量较大，坡体表层土体吸水膨胀，各特征点产生向坡外的位移，由于渗透力的大小与雨强呈正相关；总之雨强越大，边坡的水平位移显著增大。雨停后，土体仍然产生较小的水平位移，这是由于雨强较大时，雨停后边坡内部水分会下渗，产生渗透力，土体持续变形。第三级边坡的土体水平位移最大,说明强降雨时多级边坡的坡顶处最易受影响。

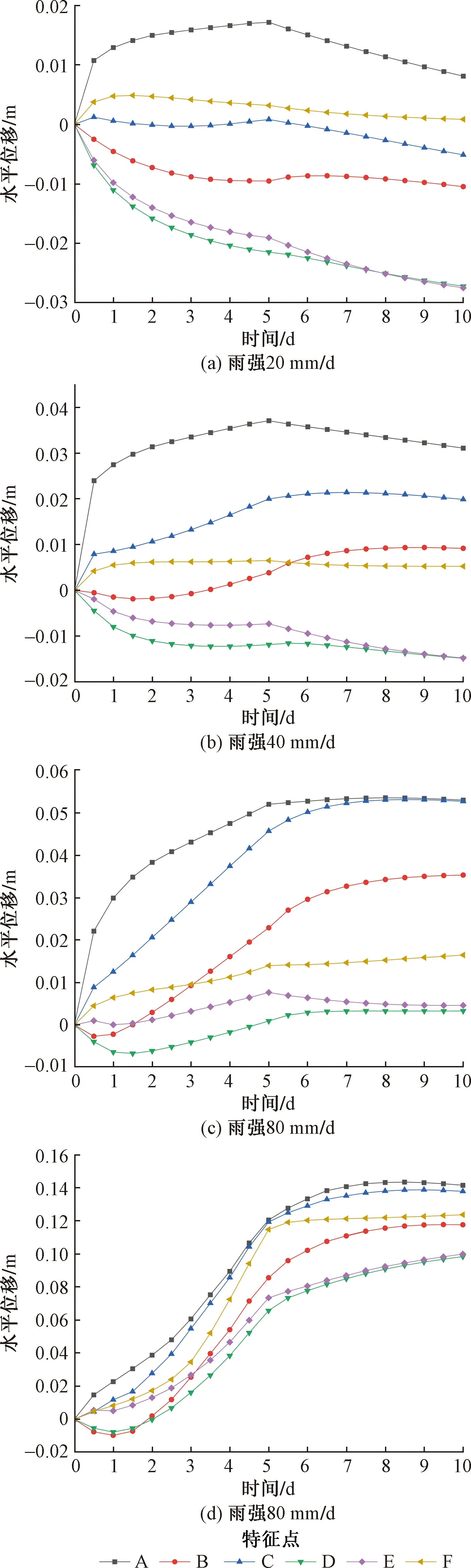
图6 边坡水平位移随雨强和时间的变化关系Fig.6 Displacement diagram of characteristic points of slope under different rain intensity after reinforcement

3.3 降雨入渗对锚杆轴力的影响

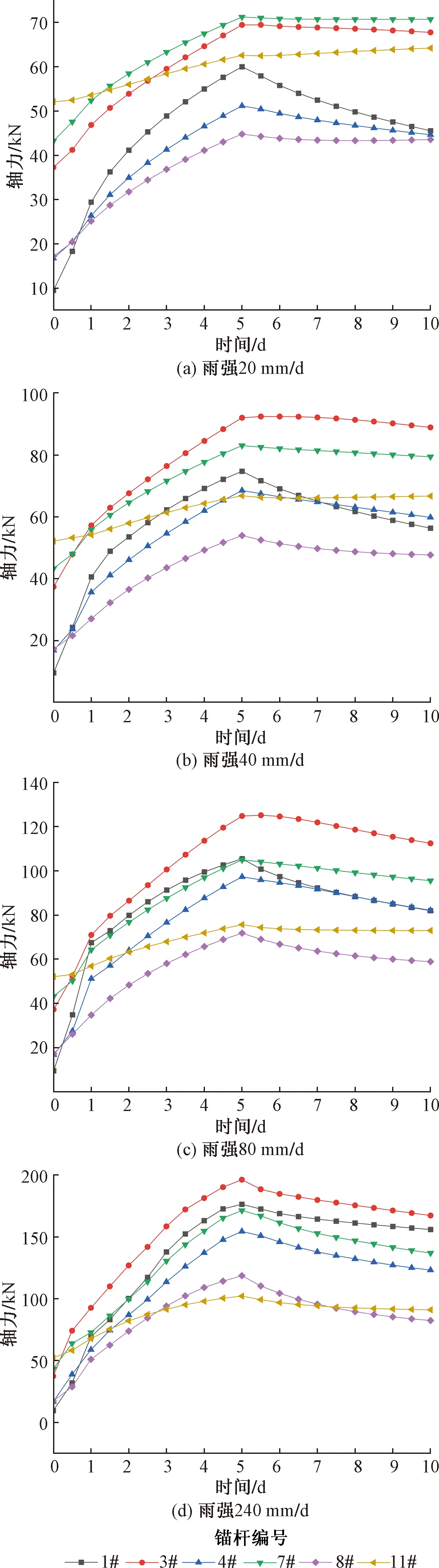
图7 不同雨强下边锚杆轴力图Fig.7 Anchor axial diagram under different rain intensity

选取每一级边坡的坡顶和坡脚处锚杆轴力进行分析，第三级边坡的锚杆为1#和3#；第二级为4#和7#；第一级为8#和11#。锚杆轴力与降雨时长的关系如图7所示。可以看出，降雨持续进行，边坡各锚杆的轴力呈增大的趋势，各锚杆的轴力增量与降雨时长近似呈线性分布；停雨后，锚杆轴力缓慢降低。在同一级边坡内，坡脚处的锚杆轴力值大于坡顶处锚杆。当雨强为20 mm/d时，同一级边坡内，锚杆轴力大小与锚杆位置到该级边坡坡顶的距离成正相关。降雨后第一级边坡的8#锚杆轴力最小，第二级边坡的7#锚杆轴力最大。当雨强为40、80、240 mm/d时，第一级边坡的8#锚杆轴力最小，第三级边坡的3#锚杆轴力最大，说明平台能有效减小坡面土压力。在降雨过程中，第三级边坡上的锚杆轴力增量大于其他两级边坡，因为第三级边坡的水平位移最大。进行边坡锚杆设计与监测时，应重点分析第三级边坡上锚杆。

图8 降雨24 h后各工况边坡剪应力分布Fig.8 Distribution of pore water pressure of slope under various working conditions after 24 h rainfall

3.4 降雨入渗对边坡剪应力的影响

不同雨强下边坡剪应力分布如图8所示，可以看出，降雨入渗过程中，边坡剪应力分布等值线大致上与坡面平行，且每一级边坡坡脚附近剪应力较大，雨强越大，坡面剪应力越大，每级边坡坡脚处易发生剪切破坏，这是由于降雨会引起边坡内积水和水在土体内渗流，积水产生静水压力，渗流产生渗透力；静水压力大小与水头成正比，会对边坡产生下滑推力；雨强越大，地下水位上升越快，静水压力和渗透力越大，则剪应力增量越大。因此边坡剪应力的增量与雨强呈正相关，具体表现形式为坡顶和坡面的剪应力增加最明显，坡体内部剪应力增长幅度不大。

3.5 降雨入渗对边坡稳定性影响

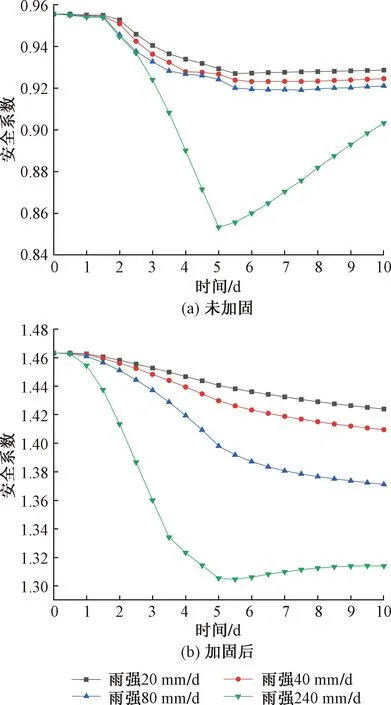
图9 边坡加固前后边坡安全系数随时间关系Fig.9 Relationship between slope safety factor and time before and after slope reinforcement

边坡加固前后的安全系数变化如图9所示。以降雨5 d为例，雨强分别为20、40、80、240 mm/d时，边坡未加固时，边坡的稳定性安全系数分别为0.929、0.926、0.924和0.853。降幅分别为2.7%、3.0%、3.2%和10.7%；锚杆加固后，边坡的稳定性安全系数分别为1.440、1.430、1.399和1.305。降幅分别为1.6%、2.3%、4.4%和10.9%。降雨作用下，两类边坡的安全系数均随着降雨持时的增加而降低，雨强越大，边坡重度增加、下滑力越大，安全系数降低得越明显。雨停后，雨强为20、40、80 mm/d 时，未加固边坡的安全系数基本不变，但加固边坡的安全系数仍然降低；降雨强度为 240 mm/d 时，未加固和加固边坡的安全系数均增大。同一降雨工况下，锚杆加固边坡的安全系数均大于未加固边坡，说明锚杆能有效增强边坡稳定性，雨强较小时，锚杆加固边坡的安全系数降低较小，雨强较大时，加固边坡的安全系数降低也较大。