压缩空气储能系统中高温叶轮瞬态热-固耦合分析
2022-11-03刘小明
刘小明
(沈阳鼓风机集团股份有限公司,辽宁沈阳 110869)
1 概述
随着我国能源产业的结构优化,各类储能系统蓬勃发展,其中压缩空气储能作为一项新兴产业,受到了多方关注。
绝热式压缩空气储能在压缩过程中对压缩热进行回收储存,在膨胀发电阶段作为热源对气体进行补热,整体热效率较高,运行过程中无需外加热源,是目前的主流研究方向。但对压缩热回收的高温度需求,对压缩机的开发提出了不同于常用空气压缩机的特殊使用条件,使设备的制造难度大幅度增加。
离心式压缩机通过旋转叶轮旋转为通流气体做功,提升气体压力,同时由于压缩过程中的效率损失提升了气体温度,常规压缩过程为了保证整机在接近等温压缩下运行,采用逐级冷却模式运行。绝热式空气储能系统的特殊要求,使其空气压缩机的设计与常规空气压缩机存在差异,不再追求等温压缩的高压缩效率,而是采用逐级升温压缩模式。压缩机的部分叶轮在高温工况下运行,由于叶轮的工作温度是逐次上升的,最高运行温度可达到接近400℃。同时由于储能电站采用储能-释能的循环运行模式,压缩机处于频繁的启停之中,压缩机叶轮在高温运行与低温待机两个状态间循环交替。
叶轮工作在高速旋转的离心力以及运行温度波动合力之下,在温度变化时,叶轮内外表面的温度会产生循环应力和循环应变,有可能最终导致龟裂破坏的现象。这些复杂的载荷、苛刻的环境对设备材料的疲劳性造成很大影响,对材料的高温性能提出了很大的挑战。在设备使用周期内,能否安全运行,及对其使用寿命的准确预测,直接关系到生产及人身安全。因此需要深入研究叶轮在高温循环载荷下的强度和疲劳安全性。
本文以某储能压缩机项目中一个高温运行叶轮为样本,利用ANSYS Workbench软件对压缩机叶轮瞬态的热-固温度应力进行了耦合分析,研究了启动运行过程中叶轮由于温差带来的热应力数值计算过程。
2 叶轮载荷分析及加载
本次分析叶轮为一闭式三元叶轮,其设计工作温度为350℃,环境温度为22℃。叶轮有限元模型如图1所示。

图1 叶轮有限元模型
叶轮在启动、负载、停止变化等过渡状态中,随着传热的变化,叶轮在启停过程中需要考虑温度差带来的应力载荷。对于旋转叶轮的单一流道,可以认为是气流在流道中流动的强制对流换热过程,此过程中叶轮工作温度由环境温度22℃上升至350℃。根据叶轮的实际对流升温以及热应力可能出现的情况,对叶轮的分析载荷施加对流换热系数和流体温度两个参数,以启动关闭压缩机为一个循环,经过升温、保温及降温过程,用ANSYS软件瞬态热分析模块对这一过程进行瞬态温度场计算。
强制换热的规律可表述为:

式中,Nu为努谢尔数,又称无因次换热系数,表征对流换热的强烈程度;Re为雷诺数,是强制对流的一个重要相似性准则;Pr为普朗特数,为表征热量传递的相似程度;ν为流体在定性温度下的动力黏度,m2·s;l为特征尺寸长度,本次计算中以沿平板(小曲面)流动进行换热计算;v为流体在定性温度下的流速,m/s;h为对流换热系数,W/m2·K;λ为流体在定性温度下的导热系数,W/m2·K。
根据强制对流换热的传热学结论,强制对流换热Nu的准则方程如下。
(1)当Re<5×105,此时流体处于层流区,准则方程为Num=0.664Rem0.5Prm1/3。
(2)当5×105<Re<107,此时流体处于湍流区,准则方程为Num=0.037(Rem4/5-23500)Pr1/3。在本项目中,特征流道长度l=0.17m,叶轮入口主流气体流速为55m/s,叶轮出口气体流速为190m/s,查得空气在这两个状态下的物性参数,根据计算所得的Re,得到两个点位上的Nu和该点的换热系数,见表1。根据以上结果,考虑叶轮旋转流动过程中的换热损失以及计算的简便性,对整个流道表面的强制对流换热系数确定为60W/m2·K。

表1 各点的特征参数汇总
根据叶轮的实际对流升温以及热应力可能出现的情况,对叶轮施加对流换热系数和温度两个载荷。启动-关闭压缩机为一个循环,叶轮运行时,内部气体温度经过升温-保温-降温过程,用ANSYS软件瞬态热分析模块对这一过程进行瞬态温度场计算,得出叶轮内外温度曲线(图2),当运行时间在6000s左右时,叶轮的内外部温度一致,因此讲瞬态温度场分析结束时间设定为6000s。经瞬态热分析,得到叶轮各个载荷步的温度,将该温度作为叶轮热固耦合分析的热载荷,导入到结构分析中,实现载荷的施加,同时施加运行速度。将叶轮工作状态下离心力、热应力两部分载荷均加入计算模型。应用热-固耦合方法对叶轮进行结构强度计算。
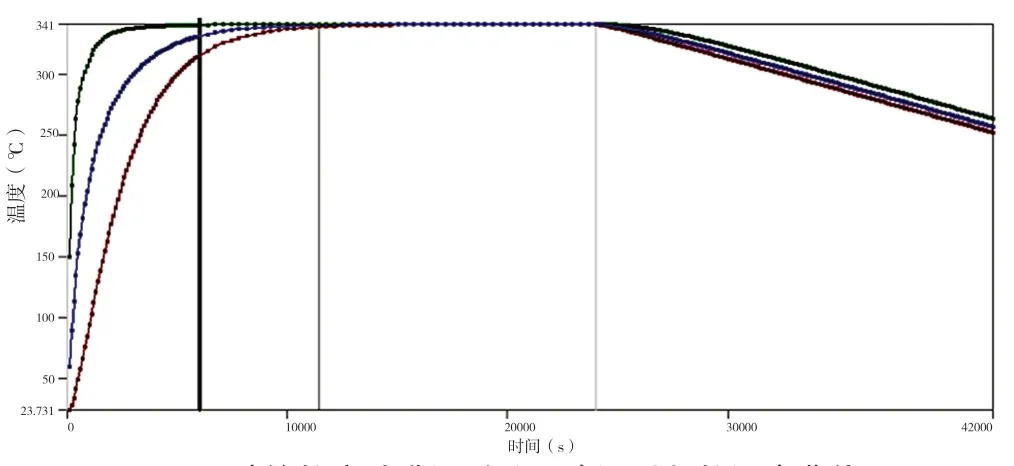
图2 叶轮的启动升温-保温-降温过程的温度曲线
3 叶轮内耦合分析结果
从图2可以看出,叶轮表面的温度首先达到最高温度,而叶轮内部温度传递速度慢,温度上升滞后。这个差别在同一时刻会产生温度梯度,对叶轮施加热应力载荷。在升温过程中,叶轮的内外温差先加大后缩小,在6000s左右时内外温度趋于一致,温度随时间的变化规律如图3所示。
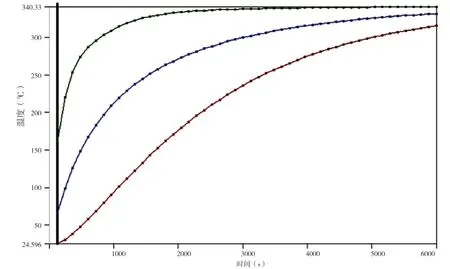
图3 叶轮温度随时间的变化(前6000s)
图4是在0~6000s的时间历程中,某一时间下叶轮的温度场、热应力场(无转速载荷)和应力场(施加转速)的分布云图。从图中可以看出叶片各部分瞬时的温度分布基本相同,在叶片的前缘和尾缘温度较高,在叶片与轴盘和盖盘连接位置区域,由于结构的不连续导致该区域应力集中,应力比较大。这些位置的热对流系数数值较大,温差随着时间的推移而逐渐减小。
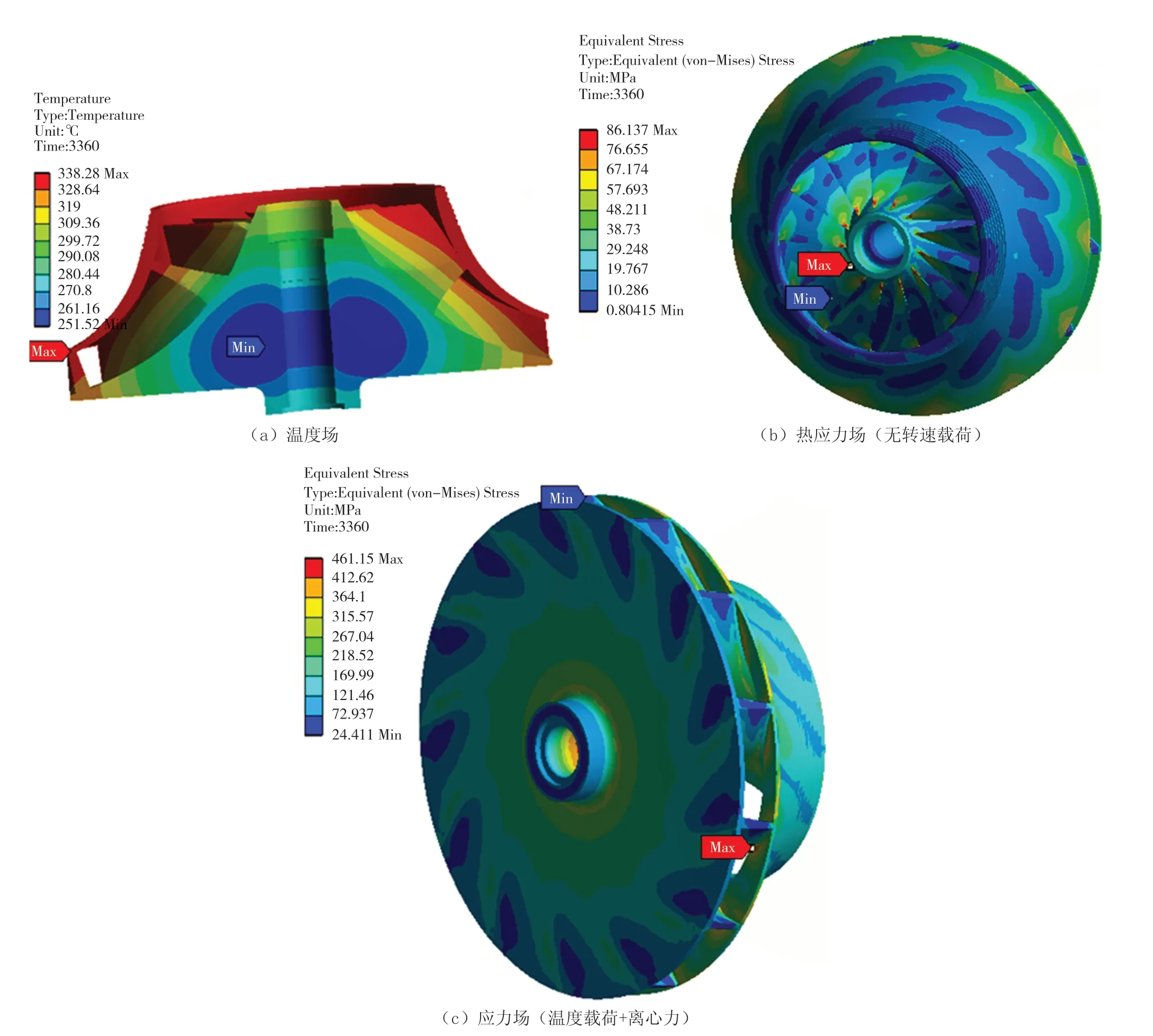
图4 某一时间叶轮的温度场和应力场分布云图
4 结论
本文基于ANSYS Workbench软件,选取高温工况下的一个叶轮,对叶轮分析施加热应力和离心力载荷,统筹考虑了温度场与离心力作用的影响,建立了热-固耦合分析模型,将瞬态分析所得到的的的温度场分布导入到叶轮的表面进行耦合场分析,得出以下结论:叶轮表面的温度首先达到最高温度,内部温度随时间缓慢上升,温度上升滞后,温升的差别必然产生温度梯度,对叶轮施加热应力载荷,在升温过程中,叶轮表面和内部温差先加大后缩小,随着时间的推进,叶片各部分的温度均不断上升,温差也越来越小,热应力也越小,最后至0;不同瞬时的温度分布基本相同,即叶片的前缘和尾缘温度较高,温差随着时间的推移而逐渐减小。
