生成与查询螺旋矩阵的在线算法研究

彭海洋

(河南牧业经济学院,河南 郑州 475000)

1 螺旋矩阵的概念与其传统离线算法

矩阵在计算机中通常用于映射线性空间内的运动,特别是对于图形学方面能够方便地进行变换等操作。 螺旋矩阵作为矩阵的一种,自身的规律性可使其作为密钥等应用于加密或其他算法中[1]。 螺旋矩阵即一个由整数填充的二维矩阵,从左上角的值为初值,向顺时针方向依次递增,按照“右-下-左-上”的顺序依次对矩阵各项赋值,如此循环直至填充矩阵所有空间。对于空间而言,一般将一个n×n大小的矩阵称为n阶矩阵。 螺旋矩阵的各项值会随阶数n的不同产生变化,如图1 所示。

图1 4 阶螺旋矩阵和5 阶螺旋矩阵

在实际应用中,螺旋矩阵的阶数具有任意性,通常需要以指定阶数作为参数,由此生成一个特定阶数的矩阵。 目前,构建特定阶数的螺旋矩阵可使用模拟算法:定义矩阵边长为n,以一个二维数组matrix[n][n]作为储存矩阵的数据结构。 从matrix[1][1]开始,按照规律依次将一个递增的值赋予各项[2]。 如算法1 所示,这种预先将矩阵内容存储在内存中的算法,可称为离线算法。

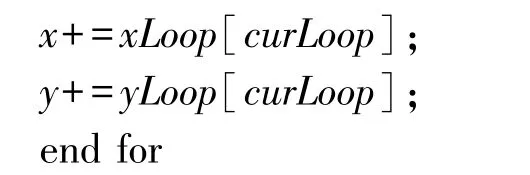
对于生成螺旋矩阵问题,可利用算法1 将矩阵构建完成后,依次循环输出各项值。 由于n阶矩阵共有n2项,所以在理想情况下利用此算法,构建时将循环n2次,输出时再次循环n2次。 设算法中所有语句频度之和为f(n),则有:

对于查询螺旋矩阵问题,同样可先行构建完整矩阵。 由于这些算法一般由高级程序设计语言编写,且作为储存结构的二维数组是顺序表,各项物理地址相邻,具有随机存储的特性。 因此,无须循环即可进入所需地址空间并返回相应值。 即在项数为n2的螺旋矩阵中,查询某项值的平均查找长度为:

由此可见,在查询问题中,语句频度为:

当n充分大时,f1(n) 与f2(n)皆与n2同阶,记作T(n)=O(f(n))= O(n2)。 所以此算法在这两种问题上的时间复杂度同为O(n2)。

仅从时间效率上来看,虽然算法1 的求解速度尚可接受,但在整体上依然存在局限性。 由于在求解中占用的临时工作单位数为n2,则在生成与查询问题中,对每一项都存在n2-1 规模的空间浪费。 以C++语言为例,通过实验得知,在VC 环境下,若以在栈区分配数组空间的方式编写程序,当n大于10 000 时就会因栈内存不足导致编译终止,即无法计算10 000 阶及以上阶数的螺旋矩阵。

2 螺旋矩阵在线算法的假设与分析

虽然可以通过在堆区手动分配内存的方式计算更大阶数的螺旋矩阵,但在实际应用中求解较大阶数的螺旋矩阵所需时间与空间的代价或不可接受。 算法1的不足在于借用了庞大的辅助数组,通过观察可发现,螺旋矩阵的每一项数值仅与其矩阵阶数有关。 即当螺旋矩阵的阶数n被确定后,矩阵第i项的值随之确定,此值记作matrixI。 同时无论阶数n如何变化,矩阵排布规律依然不变。 所以,可先行假设matrixI与其项数i对于所在矩阵的阶数n有简单对照关系,且此对照关系能够封装为函数,在程序中通过少量计算求值。 如式(4)所示:

在推导SpiralMatrix 函数的具体算法之前,可先罗列目前可用的参数以供辅助研究:(1)当前矩阵项数i:由用户查询时输入,或在生成时作为循环参数依次传入函数。 (2)矩阵阶数n:此值由用户指定,控制当前矩阵大小。

求解螺旋矩阵第i项值时,可将项数i转化为坐标xy后计算。 由于矩阵外环的值可由四角定位,其值也与阶数n有明显关系,但对于内层环而言,各环变换皆不相同,难以通过简单计算求值。 观察规律后发现:一个阶数为n的螺旋矩阵,皆能拆为「n/2层循环递增的单环,且内环初始值为外环末值+1。 即矩阵可拆分为多层单环,求解内环时,可将其内环作为阶数是当前环大小的矩阵外环,求值后再次累加各外环末值,为方便计算,本文将最外环定义为0 环。 具体如图2 所示。

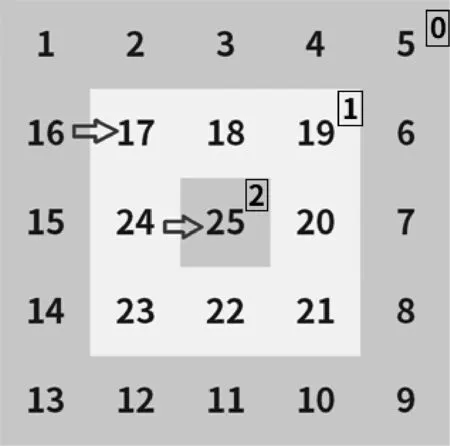
图2 螺旋矩阵各项空间关系

于是,对于一种用于生成与查询螺旋矩阵的在线算法,需要解决以下几个问题:(1)输入项数i,得到对应坐标xy;(2)通过坐标得到当前项所在层数;(3)求解在相应阶数的螺旋矩阵中,保证xy坐标为其外环时所对应的值;(4)循环累加各外环末值;(5)返回最终值。 若以算法方式描述,如算法2 与算法3 所示。

3 螺旋矩阵在线算法的推导

3.1 由项数i 计算对应坐标

本文为方便理解,设置“1”为初始值,代替计算机常用初值“0”。 在可视为二维数组的矩阵中,当前项数值每增大一个阶数值(矩阵边长),其y坐标就增加1,所以“项数i/阶数n”的商即为第i项所对应y坐标。同样,二者相除后所得余数即为x坐标。

在大多编程语言中可通过“%”运算符直接求得余数,但当被除数同为阶数时,即当目标项位于矩阵右边界时,所得商为0。 为了保持算法的统一,尽量将需要判断的地方以数学方式计算。 所以在进行除法与求余操作前,可先将项数i值-1,使“0”暂时作为初值代入计算,最后将结果+1,补回先前扣除值。 计算公式如式(5)与式(6)所示。

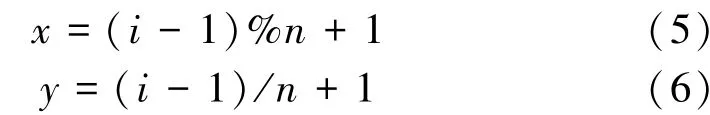
3.2 由二维坐标计算当前所在层

明显看出,阶数为n的螺旋矩阵最大层数为「n/2,此值记作deep,如式(7)所示。 同时,横纵坐标皆为deep的项即为所在矩阵的中心点。 所以若要计算当前坐标所在层数,只需计算与中心坐标的距离,再用最大层数deep减去该值。

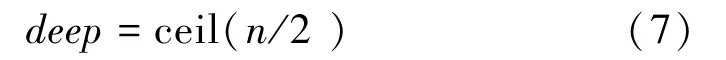
这里所求距离基于矩阵空间,与计算物理空间距离不同。 首先计算x坐标与y坐标相对中心线的距离,然后比较两者大小,其中与中心线较远的值为当前坐标在矩阵空间下相较其矩阵中心的距离,即当前所在层,或称当前所在深度,记作curDeep。 本文设定最外层的深度为0,所以在得到curDeep的结果后再次-1。 如式(8)所示。

但是,通过实践发现,式(7)的求解算法只在奇数阶的矩阵中能够得到正确值。 对于偶数矩阵而言,其中心坐标并不对应任何一项。 从空间上看,由螺旋矩阵最后4 项包围。 所以,式(7)会将本处同一层的4 项计算出不同的深度。 解决方案是抛弃层数只能为整数的固有思维,将偶数阶的层数设定在两个整数之间,即为层数deep额外增加0.5。 同样,为保持算法统一,可将奇偶数的判定值取反后作为额外增加值的权重。 改进后的算法如式(9)所示。

3.3 求解坐标为外环时的数值

当前xy坐标值是基于n阶矩阵所对应的空间位置,若将所处位置视为外环,则必须将“此处深度为0”作为条件求得所符合的新阶数,同时计算基于此阶数下对应的坐标。 通过观察发现,当前深度每增加1,目标阶数随之减少2。 因为后续仍需要完整矩阵阶数n,所以新定义当前阶数为curN,并由式(10)赋值。

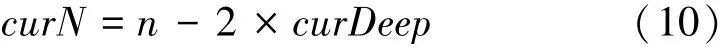
坐标方面,首先设定矩阵坐标原点在左上角,定义为(1,1)。 则坐标的更新实际上是将坐标原点由(1,1)更改为(curDeep,curDeep)的操作,仅需要通过与上文的当前深度值curDeep相减,即可正确更新坐标。 由于先前坐标不再使用,为节省空间可直接修改坐标值。 如式(11)所示。

当xy坐标原先就处于外环时,所减去的深度值为0,保持其值不变。 这就是本文定义最外环深度为0 的原因。

现在,问题可暂时转化为:一个宽度为curN的四边环,各值以顺时针反方向递增,保证xy在其环上,求对应的值。

对于每一个环,初值总为1,末值可看作从初值累加四次边长-1 的值,即curN-1,记作last, 由式(12)赋值。

为方便研究,可先在空间上将环从左上角到右下角分开,使其成为左下部分与右上部分。 对于左下部分各值,可视为以先从Y 轴向下再从X 轴向右的顺序依次“远离”末值。 由于不存在同时在两个方向上的“移动”,则X 轴与Y 轴分别与末值所在坐标的差值之和,即为与末值空间上的距离,然后用末值减去这个距离,得到处于左下部分的项的值。 定义为valueI_left。由末值坐标(1,2),得出式(13)。

同理,对于右上部分各值,可视为依次“远离”初值,且距离越远数值越大,该值定义为valueI_right。 由末值坐标(1,2),得出式(14)。

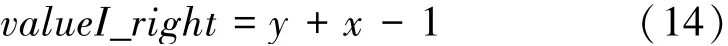
可见,当坐标y值大于x值时,此项位于左下部分,反之处于右上部分。 可利用三目运算符,将式(13)与式(14)合成式(15),并把值合并定义为valueI。

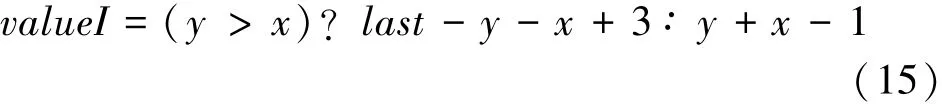
至此,已获得可构建出矩阵的所有数据,不妨先行验证一次。 本文使用for 循环语句,定义整型变量I,循环自增至n2,以I为参数,求出对应值后输出,同时每输出n个值后换行。 设置n值为12,构建12 阶矩阵作为示例,如图3 所示。 输出符合预期,只需再求出各外环末值之和,便可构建正确的螺旋矩阵。

图3 螺旋旋矩拆解为各单环

3.4 求解各外环末值之和

由式(12)可计算出某一阶外环的末值。 对于求解各外环末值之和问题,可从当前矩阵最外环,即深度为0 的环开始,到当前深度环为止,循环使用式(12)求出对应环末值并累加。 本文研究在线算法的目的之一,是要规避算法中出现的循环结构。 为得到简洁的公式,先由循环思想出发,定义deepI为循环计算中累计求值所使用的当前阶数,循环语句为式(16)。

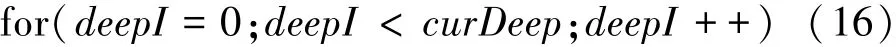
定义各外环末值之和为acc,在循环语句中累加,如式(17)所示。

通过通项公式简单计算,可得到式(19),这是一个不包含deepI的公式,计算结果为各外环末值之和。 最后将式(15)中的valueI与acc相加,即可直接计算得到当前项在螺旋矩阵中的值。

最后,同样以12 阶为例,顺序计算后输出,检验算法准确度,如图4 所示。

图4 12 阶的螺旋矩阵

可以看到,在生成螺旋矩阵方面,本文研究的算法可准确计算矩阵各项值,所以本算法也可应用在查询螺旋矩阵问题上。

4 螺旋矩阵在线算法与传统离线算法在性能上的对比

在生成螺旋矩阵问题中,由于不可避免地需要遍历一次大小为n2的矩阵,则本算法的时间复杂度与算法1 的时间复杂度相同,为O(n2)。 而在空间上,本算法省去了预先构建矩阵的操作,无需使用辅助数组,空间复杂度为S(1),小于算法1 的空间复杂度S(n2),性能上整体优于算法1。 在查询螺旋矩阵问题中,同样因为无需提前计算矩阵各值,所以本算法的时间复杂度降至O(1),空间复杂度同样降至S(1)。 在性能上全面优于算法1。

如图5、图6、图7 和图8 所示,展示了传统离线算法与在线算法在求解这两种问题时分别在时间与空间上的差异。 其中编译与运行环境为VC,所有变量在栈区定义,查询项为项数中间值n2/2,记录时间不包括输入与输出所占的时间。 所有结果为多次实验取平均值。

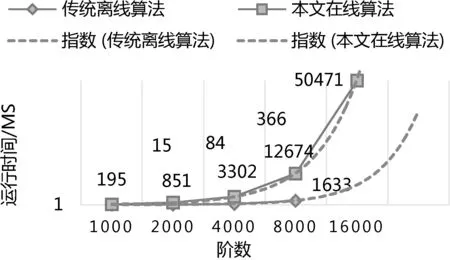
图5 生成操作的时间对比

图6 生成操作的内存空间对比

图7 查询操作的时间对比

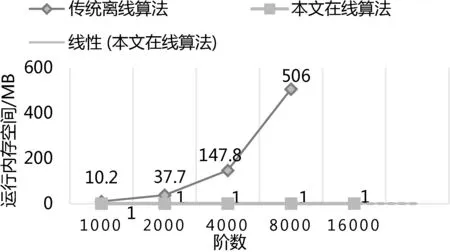
图8 查询操作的内存空间对比

从图表可直观看出,除了在生成操作上在线算法较常规算法有系数级别的额外时间损耗外,对于其余3种操作,在线算法在效率上都远远优于常规算法,特别是在线算法也可计算常规算法无法求解的大阶数螺旋矩阵。