基于二型模糊系统多源异质信息目标身份类别推理方法*
2022-11-02贾世伟顾嘉耀郑天宇钟继鸿
贾世伟,顾嘉耀,郑天宇,钟继鸿,张 进
(上海机电工程研究所·上海·201109)
0 引 言
在多源异质目标信息量测中,受传感器精度的影响 ,传统的一型模糊集只能反映传感器量测点值的隶属度函数,并不能反映隶属度函数本身的不确定性,而基于二型模糊集的目标身份推理方法[1]则可用于解决该问题。
基于模糊系统的推理方法是规则推理的一种实现方式,典型的应用于纯模糊系统的模糊推理方法有:Mamdani算法[2-3]、全蕴涵三I算法[4]及其改进算法[5],以及合成推理模型(Compositio-nal Rule of Inference, CRI)算法。其中,CRI算法最初由Zadeh教授提出,为模糊推理提供了一种运用模糊关系和复合运算进行推理的框架;Mamdani算法是目前实际应用最为广泛的模糊推理算法之一。近年来,基于模糊集框架下的推理算法多与其他智能学习算法结合使用。Ishibuchi等研究了神经元连接区间权值的模糊神经网络方法[6],并设计了一种基于模糊规则推理的神经网络算法,引入代价函数来决定输出结果的区间模糊程度;陈晨等利用先验信息构建模糊规则库,并在此基础上提出了一种基于规则库的置信度推理算法[7]。此外,相关的研究还包括基于证据理论的方法[8-9],利用mass函数描述前件信息与结论的不确定性。然而,D-S证据理论已被证明在先验信息高冲突情况下存在局限性,且推理结果的好坏很大程度上取决于mass函数构造得是否准确[9]。
本文在构建一型模糊系统的基础上,借助遗传优化算法对模糊推理规则进行优化,在确定模糊划分区间的前提下得到最优隶属度函数。针对多源异质目标信息测量的实际应用场景,考虑传感器量测偏差问题,通过嵌入一型模糊集三角型隶属度函数,构造对应二型模糊集,并给出具体的推导过程,设计了基于二型模糊集的目标身份类别推理方法,以验证二型模糊推理系统的可行性。
1 二型模糊推理系统构建
对于二型模糊集的建立,需要在一型模糊集训练的基础上,建立起对目标数据的经验描述,也称为领域专家判断[10],这也是二型模糊集与一型模糊集在形式上的最大区别。首先构建一型模糊推理系统,然后构建基于Tag数据集的三角二型模糊集,最后对二型模糊系统采用遗传算法进行优化设计。
1.1 一型模糊推理系统构建
一般的一型模糊逻辑系统主要由模糊规则和模糊推理算法两部分组成。其中,模糊规则在本文研究中用于描述在特定工作场景下,多源目标信息测量传感器采集得到的信息特征量与输出识别结果间的不确定性关系。在该描述中,既包含了在不同环境中不同噪声对输出结果的影响,也体现了规则本身所具有的不确定性。
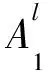
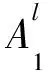
(1)
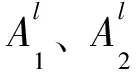
(2)

(3)
(4)

在推导二型模糊集隶属度函数过程中,需要用到的基本运算法则有
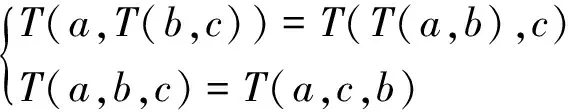
(5)
在多源异质目标量测中,各个传感器的测量精度不同于初始时空误差,训练样本数据各个属性值的可信度并不相同。因此,需要对各个训练数据进行可信度的判断,对于可信度较高的数据给予高置信度加权,对于可信度较低的数据则给予低置信度加权。引进不同置信度加权值的目标身份类别归类的离散概率分布,如式(6)所示
(6)
1.2 二型模糊系统构建
在获取的经验描述中,建立数据集Tag(tk,xi),表示对于第tk类目标的经验描述区间为xi。在进行模糊集构建前,应先对所有的Tag数据集进行预处理[14]。在完成Tag数据集的预处理后,对基于Tag数据集的三角二型模糊集进行构建推导。对于普通一型模糊集,如图1所示。

图1 标准三角型一型模糊集Fig.1 Trapmf type-1 fuzzy sets
有
(7)

(8)

(9)
将对称三角隶属函数的数学解析式代入式(9)可得
(10)
为简化隶属度函数表达式,分别记A、B表达式如下
(11)

(12)
联立式(8)和式(9)可得
(13)

(14)
在此基础上,可计算获得对应三角二型模糊集的特征参数
(15)
(16)
(17)
(18)


图2 嵌入式二型模糊集Fig.2 Embedded type-2 fuzzy sets
2 二型模糊系统的遗传优化设计
对于二型模糊系统而言,输入的测量数据可以为点集,也可以为某一数值区间,也可以为区间型的二型模糊集。以下是基于三角隶属度函数的匹配度计算公式以及简单的推导过程。

(19)

(20)
Rk(x)=T(mk(x1),…,mk(xi))
(21)
(22)

(23)
其中,Ac表示二型模糊集的平均势;card表示模糊集的势;μTi(x)表示对应模糊集的隶属度函数。根据1.2节De Luca和Termini定义,如式(24)所示
(24)
可将式(23)简化成式(25)
(25)
至此给出了两种数据输入形式下mk(xi)以及对应Rk(x)的表达式。在本文应用场景下,通常认为数据样本集Tar(v(k),f(k),M1(k),M2(k),M3(k))分别对应目标的速度、辐射以及三种模板匹配的图像信息,尽管速度和目标辐射信息采样形式为点集,但由于具有量测误差与估计误差,因此需要对点集进行区间域的模糊描述。模板匹配抽象后的TarM(M1(k),M2(k),M3(k)),已通过遗传优化完成模板寻优,因此该部分样本输入仍保留点集形式。在此分析基础上,显然Tar(v(k),f(k),M1(k),M2(k),M3(k))具有点值和区间值两种数据输入形式。
按照以下步骤实现遗传算法对模糊系统的优化[16]:
步骤1:设置初代种群。设定正确识别率门限W0以及遗传代数上限N0。
步骤2:种群的选择保留。
若P0=max{PACU(Cmj)}>W0或者m>N0,转向第4步,其中PACU(Cmj)是指第Cmj个编码串对应的模糊系统;
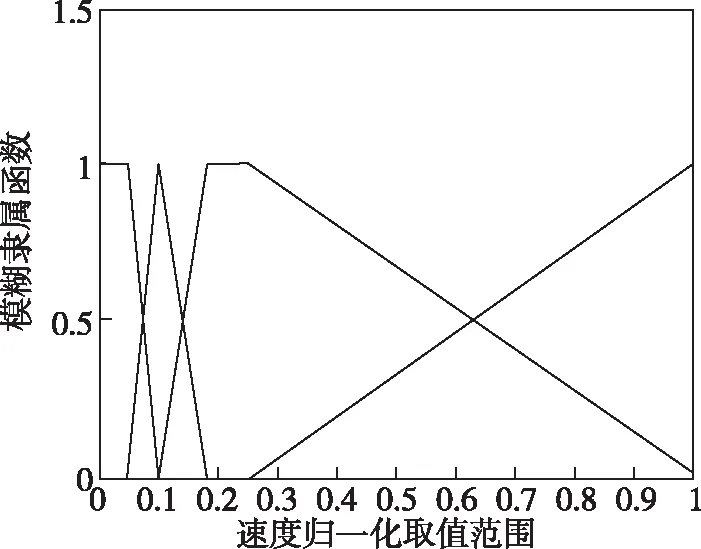
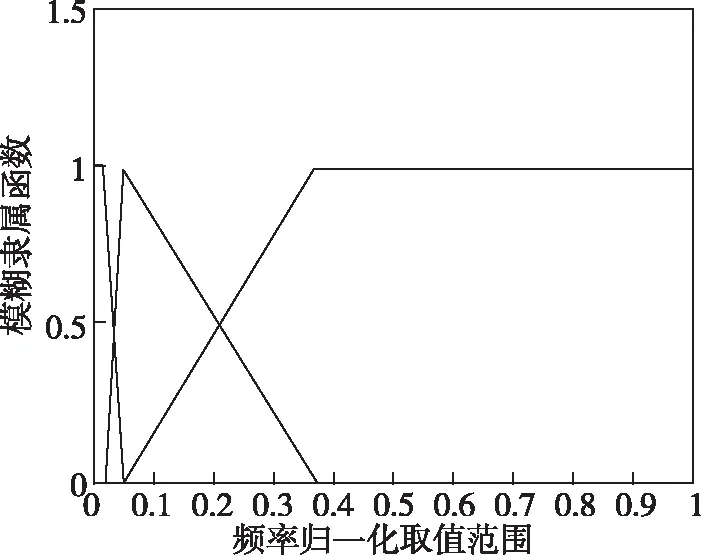
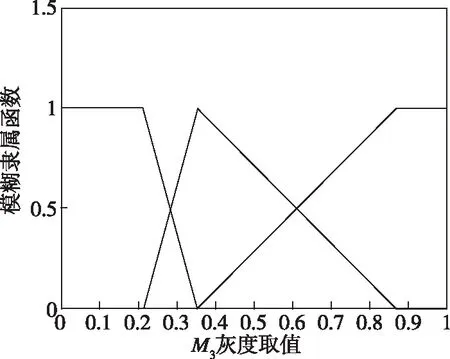
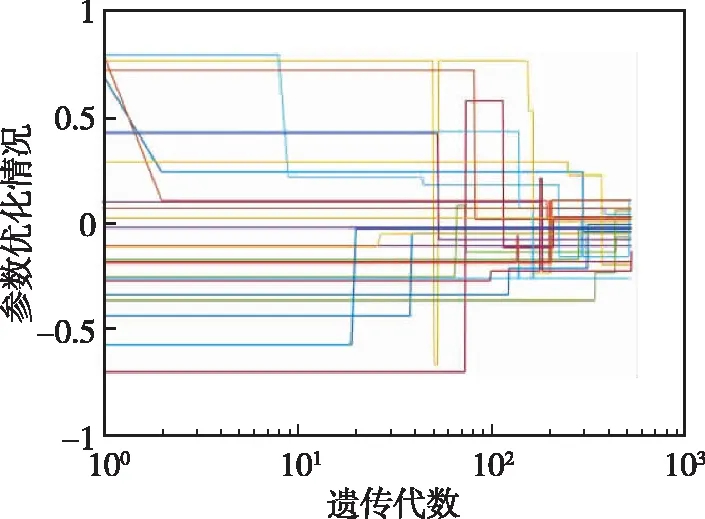
若P0=max{PACU(Cmj)}≤W0并且m 步骤3:种群选择。 同时令m=m+1,转向第2步。 步骤4:输出近似最优解。 以上即为具有三角隶属度函数的一型模糊集构建二型模糊推理系统的完整步骤,在此基础上对二型模糊系统进行遗传优化算法设计,图3所示为算法改进框图。 图3 二型模糊推理系统算法实现流程图Fig.3 Flow chart of algorithm implementation of type-2 fuzzy inference system 运动目标Tar(v,f,M1,M2,M3)为含有五维特征值的向量组,在本次仿真中,以速度v、目标辐射f以及目标图像Mk为规则前件,异类目标集合(Tar1,Tar2,Tar3)作为后件的目标集产生数据集,每一类数值均含有T(v,f,Mk),k=1,2,3,以及预设标签值y代表目标身份。首先建立样本数据集,然后对一型模糊推理系统进行遗传优化,完成训练集的建立,训练结果为目标速度维度、目标辐射维度以及3个目标在模板匹配度维度上的隶属度函数。在获得基于模糊推理规则前件的最优一型隶属度函数后,以样本数据值作为经验描述,获取对应的二型模糊推理系统前件规则,最后进行遗传优化仿真,计算得到目标识别概率结果。设置正确识别率门限W0=0.95,最大遗传代数N0=1000,交换概率Pcross=0.2,变异概率Pmutate=0.4,种群规模(编码长度)J=25。 1)样本数据集建立:对于T(v(k),f(k),M1(k),M2(k),M3(k))的前二维特征量T(v(k),f(k))的数据集,取值见表1。 表1 部分仿真测试数据集 目标图像维度的部分样本数据点为3个目标匹配度数据(M1,M2,M3)。此处模板匹配相似性度量函数如下[17] (26) 归一化后的相关系数为 (27) 式中,D(i,j)为图像绝对差;Sij(m,n)为待判断区域;T(m,n)为模板图像;R(i,j)为图像匹配度归一化指标;L(k)为绝对匹配误差归一化指标。 本节中(M1,M2,M3)传递的即为R(i,j)的取值,表2给出了部分模板匹配(M1,M2,M3)的数据,并进行归一化处理。 表2 部分实验数据表格(点值) 第一类数据样本点为以(2,4,2)为均值,s11、s21为方差产生的高斯分布数据,标签值y1=1代表目标1;第二类数据样本点为以(12,55,3)为均值,s12、s22为方差产生的高斯分布数据,标签值y2=2代表目标2;第三类样本点为以(50,35,3)为均值,s31、s32为方差产生的高斯分布数据,标签值y3=3代表目标3。根据式(28)和式(29)分别生成两批仿真数据。 (28) (29) 2)最优一型模糊推理系统获取:经过以上步骤后完成了训练集建立。本次仿真中主要识别的目标包括3个(目标1、目标2、目标3),每个目标数据为200组,共计目标数据集为600组。训练目标集形式为Tar(v(k),f(k),M1(k),M2(k),M3(k)),分别代表目标的速度、辐射以及3个目标图像匹配度。将600组数据随机分成A、B两等份,每份均包含3个目标数据各100组。把数据集A作为训练数据,数据集B作为测试数据。Tar(v(k),f(k),M1(k),M2(k),M3(k))中各特征量的预设控制编码长度为25,利用遗传优化算法求解特征量对应的最优隶属度函数。 训练结果的隶属度函数如图4所示。图4(a)、图4(b)分别代表目标在速度和目标辐射二种特征维度上的隶属度函数。图4(c)、图4(d)、图4(e)则为3个目标在模板匹配度维度上的隶属度函数。 (a) 速度隶属度函数 (b) 目标辐射隶属度函数 (c) M1隶属度函数 (d) M2隶属度函数 (e) M3隶属度函数图4 一型模糊隶属度函数Fig.4 Type-1 fuzzy membership function 图5给出了一型模糊系统遗传优化算法的优化指标迭代情况以及各个优化参数的优化情况,图5(a)表明遗传算法在第568代处收敛,正确识别率为0.958;图5(b)表明遗传算法种群参数在第300代处附近初步收敛,其中每一个种群参数(用25种颜色的曲线表示)表明在该隶属度函数划分区间内编码设置的调整值。 (a) 优化指标迭代情况 (b) 编码等于25参数优化情况图5 遗传算法优化结果Fig.5 Genetic algorithm optimization results 3)二型模糊推理系统前件规则获取:在获得模糊推理规则前件的最优一型隶属度函数后,也获得了各个样本点在此隶属度函数下的适应度Yx=k,k=1,2,3,分别对应三类目标。在此基础上,每类目标分别选取Yx=k>0.9和Yx=k>0.8且Yx=k≠1的样本数据值作为经验描述,获取对应的二型模糊推理系统。其最终隶属度函数获取结果如图6所示。 4)仿真计算:由于图像维度的匹配值经历过寻优过程,因此认为在(M1,M2,M3)三维上的匹配度数据不存在二型模糊隶属度函数。在图6中给出的14个二型模糊隶属度函数对应两类情况(Yx=k>0.9或者Yx=k>0.8),每类包含的6个二型模糊隶属度函数分别对应的规则前件为(fT=1,fT=2,fT=3,vT=1,vT=2,vT=3)。部分测试集数据形式如表3所示,其中Group代表Yx=k>0.9和Yx=k>0.8的两组数据,Sd为数据生成方差. (a) 目标1辐射维度二型隶属度函数 (b) 目标2辐射维度二型隶属度函数 (c) 目标3辐射维度二型隶属度函数 (d) 目标1速度维度二型隶属度函数 (e) 目标2速度维度二型隶属度函数 (f) 目标3速度维度二型隶属度函数图6 二型模糊系统的隶属度函数训练结果Fig.6 Training results of membership function of type-2 fuzzy system 表3在原点值数据的基础上,分别给出以Sd=0.0025(Group=1)和以Sd=0.25(Group=2)为方差,生成区间型数据的左右端点ek、fk。此处需要说明的是,在实际场景中,数据方差SGroup的大小完全取决于传感器在该特征属性上的精度。对于T(v,f,M1,M2,M3)中的T(v,f)测试集数据,生成区间型数据的方差具体设置参数如表4所示,共计两组数据,其中Sv1、Sf1、Sv2、Sf2分别为两组目标数据速度和频率维度的方差。 表3 部分测试集数据(区间型) 表4 区间型测试集生成参数表 根据上述设置的参数,表5给出了两种情况下二型模糊推理系统对应的识别准确率。 表5 两种情况下二型模糊推理系统目标识别平均准确率结果对比表 根据(Sv1Sf1)、(Sv2Sf2)两种情况下的二型模糊推理系统目标身份识别结果,可以看出在考虑传感器量测偏差的情况下,设计的推理系统仍有较好的识别结果。 本文围绕多源异质信息目标识别开展研究,针对无先验前件问题,考虑到各传感器精度有限,测量值并不完全反映目标在该特征维度的取值。在一型模糊系统构建的基础上,将三角隶属度函数嵌入二型模糊集,对采集的点值型数值进行区间型数据建模。并在点值特征输入及区间型特征输入均存在误差的情况下,通过遗传优化算法得到规则前件的最优隶属度函数,在此基础上对训练得到的模糊推理系统进行仿真验证。可以看出,在考虑传感器量测偏差的情况下,设计的二型模糊推理系统对不同类型的目标仍有较好的识别结果,验证了本文方法的可行性。同时可以发现,随着传感器精度降低,采集到的点值数据方差变大,造成采集点值的可能区间变大,从而使得二型模糊推理系统性能下降,需要考虑将模糊推理方法同其他智能优化算法结合,进一步提高推理系统的鲁棒性。
3 二型模糊系统仿真验证















4 结 论
