基于响应面法的W型封严环型面优化设计

2022-11-02李神龙嵇佳佳熊伟

中国设备工程 2022年20期

关键词：波峰回归方程圆心

李神龙，嵇佳佳，熊伟

（1.中国航发长江动力有限公司研发中心，湖南岳阳 414000；2.中国航发南方工业有限公司航轴中心，湖南株洲 412000）

国内W型封严环的设计多采用国外原型机测仿，自主进行设计时主要依赖于工作积累及经验。龚雪婷等分析了操作参数和壁厚对密封性能的影响。王晨希等分析了波峰、波谷、壁厚、波高h2对W型封严环回弹性能和密封性能的影响规律。

申秀丽等探索了W形封严环关键结构参数对强度的影响，基于灵敏度分析对结构参数进一步优化。李伟平等对利用ANSYS软件APDL语言和参数化技术对金属封严环结构尺寸进行参数化建模，以增大封严环与法兰间的接触应力为目标进行结构参数优化。

本文针对W型封严环结构参数，开展封严环全参数显著性分析，得到各参数对W型封严环综合性能影响规律，并筛选出最显著参数。由于各参数的影响关系存在着耦合现象，为了考虑各参数对封严环综合性能影响，采用响应面法对W型封严环显著参数进行优化设计。

1 W型封严环设计方法

1.1 截面形状的设计

W型封严环的基本元件由与相邻元素两两相切的七个圆弧及两条直线所确定，见图1。

图1 W型封严环截面形状

1.2 W型封严环初始结构参数

已知某W型封严环工况参数（表1），W型封严环初始结构参数（表2），以初始结构参数为构型基准，开展全参数显著性分析，研究各参数对综合性能的影响程度，为下一步开展优化设计提供理论依据。

表1 工况参数

表2 初始结构参数

2 各参数对W型封严环性能影响分析

2.1 建立有限元分析模型

2.1.1 材料属性

该W型封严环采用镍基高温合金材料GH4169，在-253～700℃温度范围内具有良好的综合性能，650℃以下的屈服强度居变形高温合金的首位，并具有良好的抗疲劳、抗辐射、抗氧化、耐腐蚀性能，以及良好的加工性能、焊接性能和长期组织稳定性。对W型封严环进行应力分析时，为了更能准确的模拟材料的力学性能，选用基于Von Mises屈服准则的第四屈服理论。其基本力学性能参数见表3。

表3 材料力学性能参数

2.1.2 有限元模型简化

在有限元分析的过程中假设材料同向性、无材料缺陷且无残余应力，W型封严环成型过程中的薄壁厚度均匀。由于W型封严环为轴对称结构，且载荷和约束也具有轴对称性，因此使用平面轴对称模型对W型封严环和法兰进行结构简化。

2.1.3 有限元单元类型选择与划分

采用无扭曲的轴对称单元（CAX4R），可模拟360°的环，适用于分析具有轴对称几何形状并承受轴对称载荷的结构。对模型进行划分网格时，为了使计算更加精确，对靠近接触面的特定区域需进行网格细化，W型封严环0.01，法兰接触区域0.01，法兰非接触区域0.02。

2.1.4 载荷与边界条件设置

常温预紧压缩下，下法兰施加固定约束，上法兰施加轴向压缩位移，模拟W型封严环在工作状态时的轴向压缩，不施加压力。工况下，W型封严环开口侧施加1.76MPa的工作压差。

2.2 参数显著性分析

2.2.1 设计矩阵

取W型封严环每个参数的高水平和低水平进行设计试验，每列包含的高、低水平数相等，每行高、低水平的数目均为6个,各参数的高低水平试验设计如表4所示。

表4 试验设计

利用数值计算得到的数据样本采用最小二乘法进行拟合得到多元一次回归方程，分别得到响应值回弹率、最大等效应力、最大接触应力关于参数t、h1、h2、R1、R2等相关显著参数的回归方程，选定影响响应目标显著的结构参数。

2.2.2 各参数对回弹率的影响分析

图2所示，随着壁厚t、接触面半径R4及环高H的减小，回弹率增大；随着波峰波谷圆心距h1、波谷R2、波峰R1与接触面圆心距h2的增大，可以提升回弹率。

图2 显著参数对回弹率的影响

2.2.3 各参数对最大等效应力的影响分析

图3所示，随着壁厚t、波谷圆心距K的减小，最大等效应力降低；随着波峰R1、波谷R2、直径D、径向宽W与环高H的增大，可以降低最大等效应力。

图3 显著参数对最大等效应力的影响

2.2.4 各参数对最大接触应力的影响分析

图4所示，随着壁厚t与径向宽W的增大，最大等效应力提高；随着接触面圆心距h2、波谷圆心距K、接触面半径R4与外切圆半径R3的减小，可以增大最大等效应力。

图4 显著参数对最大接触应力的影响

3 基于响应面法的型面优化设计

通过显著性分析结果，考虑安装槽尺寸空间，选定t=0.2mm，R3=1mm，R4=3mm，H=3.4mm，保证安装及压缩间隙的前提下，应尽可能选取最大直径尺寸。综合考虑对W型封严环综合性能显著的结构参数径向宽W、波峰半径R1、波谷半径R2、波峰与波谷圆心距h1、波谷与接触面圆心距h2，采用响应面法（RSM）对以上参数进行优化设计。

响应面法（RSM）是数学方法和统计方法结合的产物。通过合理的试验设计方法组合得到一组试验方案，并经过试验得到各方案的响应目标值；利用多元二次回归方程拟合设计变量与响应目标值之间的函数关系，通过对回归方程的分析来寻求最优的参数，从而解决多变量的一种统计方法。在本文中，工况下的响应目标值结果数据通过ABAQUS软件仿真得到。

响应面法的试验设计方法有很多，如田口设计、均匀设计、中心组合设计、BOX设计等，最常用的是CCD和BBD，在因素数相同时比中心复合设计所需的试验次数少。所以在W型封严环型面的优化中采用BBD方法进行优化。

3.1 W型封严环型面优化

选取波峰半径R1取值范围为0.45～0.65，波谷半径R2取值范围为0.55～0.65，波峰与波谷圆心距h1取值范围为0.8～1.0mm、波谷与接触面圆心距h2取值范围为1.05～1.65mm，由于径向宽只对最大接触应力影响显著，为了计算效率，W取定值，取值为R2与h2之和。响应面试验设计及结果如表5所示。

表5 响应面试验设计及结果

根据表5中的数据利用最小二乘法拟合得到回归方程如下式所示：

为检验回归方程拟合的有效性，需要对回归方程进行方差分析，表6为回弹率回归方程进行的方差分析结果（仅列举一例数据及图形）。其中，P值小于0.01意味着模型是极显著的，对拟合回归方程Y1进行误差统计分析，计算多元相关系数R2值为0.8513，可见模型具有较高的精度。

表6 回弹率方差分析

图5～6中散点为以颜色表征回弹率大小的各试验点。图6横坐标为残差值，纵坐标为正态分布的百分比例，由图可见回弹率的残差沿直线分布，表明其误差呈正态分布，由此可知所提出模型预测的响应值是正常的且没有较大的偏差。图7为回弹率预测值与仿真计算值的关系图，图中各散点的横坐标值代表回弹率的仿真计算值，纵坐标值代表回弹率的预测值，由图可知，各散点均分布在相关线附近，即各散点的横纵坐标值相近，表明W型封严环回弹率的预测值与仿真计算值吻合度较高。

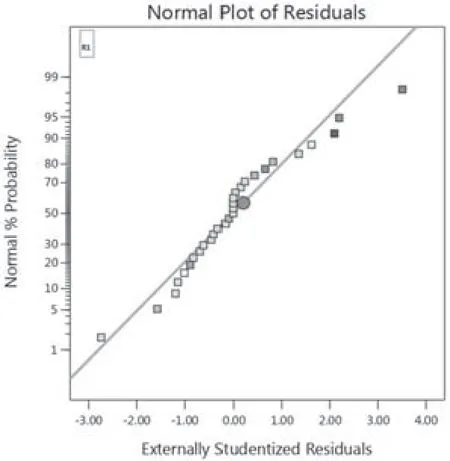
图5 回弹率残差正态概率分布图

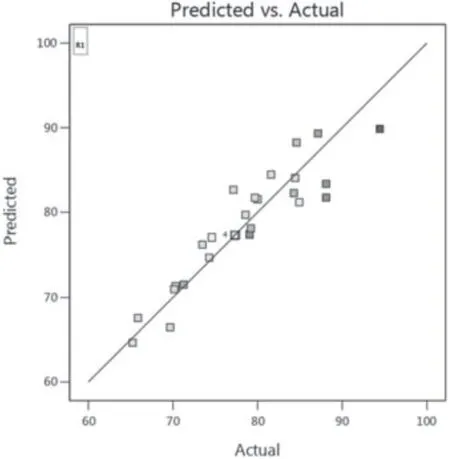
图6 回弹率的预测值与仿真计算关系

对回归方程（1）进行分析，得到R1、R2、h1及h2四参数任意组合时的期望值，期望值最大点即为最优结构参数点，如图7所示，可得优化目标回弹率的最优解为 91.12%，最大等效应力的最优解为1103.19，最大接触应力的最优解为340.87，最佳优化型面参数组合为：波峰半径R1为0.45、波谷半径R2为0.58、波峰与波谷圆心距h1为0.8、波谷与接触面半径圆心距h2为1.65。