基于不同压力下煤层气低速渗流的数值分析

陈 超，张华知

(1.四川化工职业技术学院；2.精细化工应用技术泸州市重点实验室，四川 泸州 646000)

煤层气主要成分为甲烷(CH4)，是在漫长的地质年代中经由煤层中的天然气通过运移和扩散后的剩余量，包括煤层中颗粒基质表面的吸附气、由于煤层中生成的气体超过煤岩体表面临界吸附量后在煤层孔隙和裂隙中的游离气以及溶解于水中的溶解气[1]。由于煤层既是生气层，又是储气层，因此它是一种非常规的天然气。在煤矿开采过程中，煤层气是煤矿开采过程中的有害气体，目前大部分矿井在采矿过程均采用将其抽出地表排空，致使煤层气利用率不高，回收利用率较低[2]。

对于煤层气的渗流分析，国内外学者均进行了较多研究。J L Joubert研究了煤层甲烷在湿煤中的吸附作用[3]，A.G.Kim研究了煤层甲烷在烟煤中的吸附量[4]，Gregory J.Bell进行了高压含水煤岩中煤层气的渗流实验[5]，P J.Crosdale研究了不同煤样煤层气的吸附渗流规律[6]，岑培山研究了煤体平行层理及垂直层理裂隙方向的瓦斯渗流规律[7]，万军凤等深入研究了多因素综合作用时煤岩瓦斯渗流规律[8]，公维宽等通过Avizo对煤样进行三维重构并使用CFX对其进行低压瓦斯渗流的定量分析[9]，彭守建等通过结合试验和自主研发的设备深入研究了吸附作用下煤基质的收缩效应对煤岩渗透率的影响[10]，范鹏宏等采用自行研制的含瓦斯煤准三轴渗流试验装置研究了在不同围压条件下Forchheimer型非达西渗流特性[11]。本文通过数值分析，建立了煤样中煤层气渗流的数学模型，并对其在不同压力下低速渗流的流动情况进行了数值分析。

1 物理模型及CFD计算方法

1.1 物理模型

煤样的物理模型选用已进行处理的φ50mm×100mm圆柱体寺河矿[10]，采用ICEM-CFD对建立圆柱体试件物理模型并对其进行了网格划分，将模型简化为仅有轴向坐标x和径向坐标r的二维轴对称模型。轴向的计算区域为0～0.1 m，径向由于对称且煤层气在煤样中渗流时，各向湍动均匀，故径向对称，计算区域为0～0.025 m。网格划分采用标准的矩形网格，分为轴向2 000个和径向500个，网格总数为100万个，网格划分如图1所示。

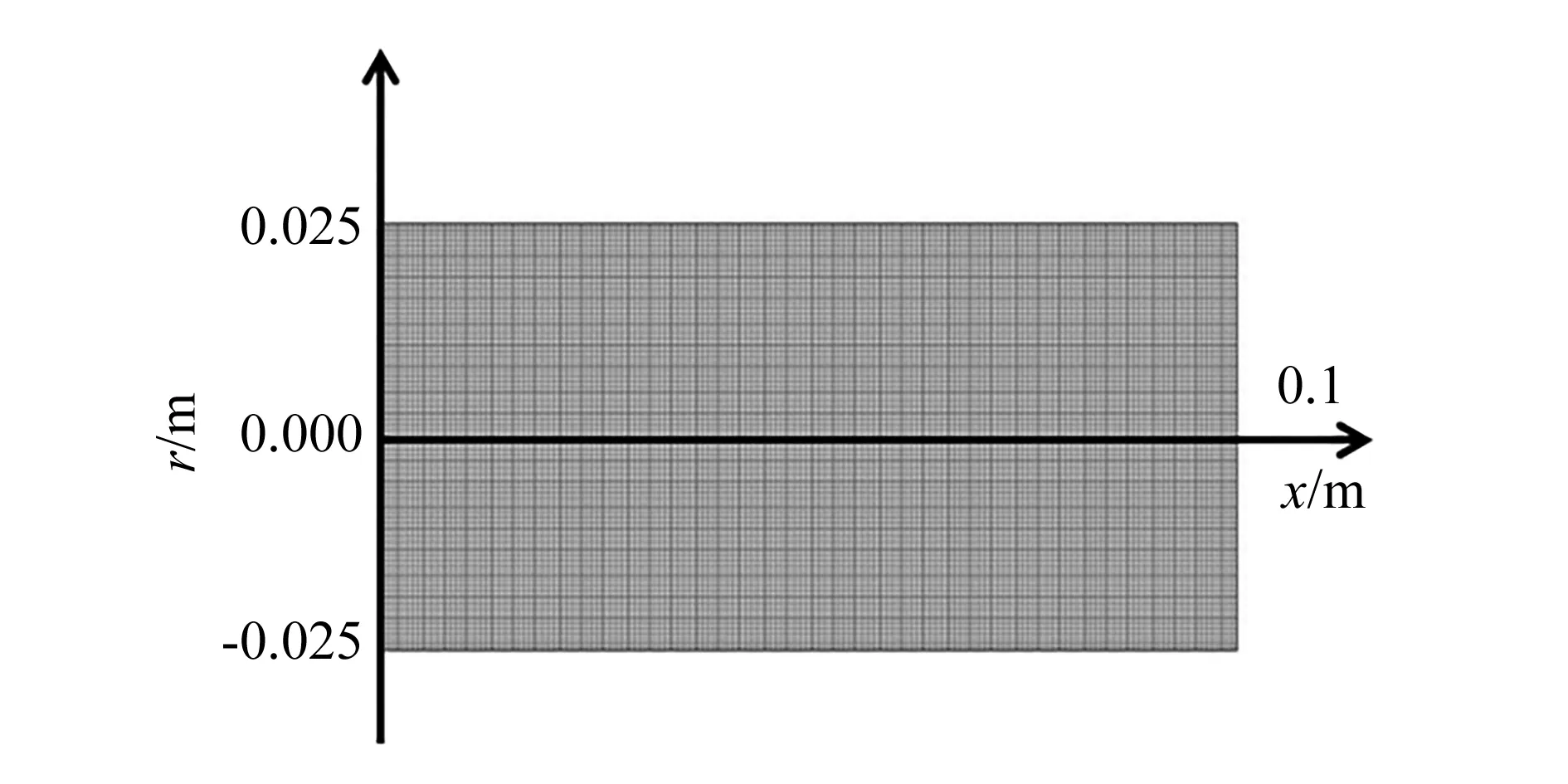
图1 网格划分

1.2 CFD计算方法

1.2.1 数学模型

在连续性方程中，质量源项Sm为单位体积多孔介质吸附气体的质量随时间的变化率，亦即多孔介质系统中吸附气体随时间的减少量；在动量方程中，动量源项Si是作用在微元体上的外部作用力；在湍流方程中，考虑到煤层气湍流为各向同性的特点，同时结合精度要求、计算机能力和时间的限制，计算式采用标准的k-ε方程。采用已推导出的质量源项和动量源项[12]，结合标准k-ε方程，分别表述如下：

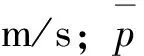
1.2.2 求解技术

结合研究内容，综合考虑精度、收敛性以及系统资源等要求，对偏微分方程选择采用PIOS二阶上风差分法进行离散，采用SIMPLE算法求解，算法流程如图2所示。偏微分方程采用PIOS二阶上风差分法离散，计算前期时间步长采用Δt=0.01 s，待计算逐渐收敛时，时间步长逐渐增大至Δt=1 s，迭代终止时间为相应压力下由实验测得的饱和吸附时间。

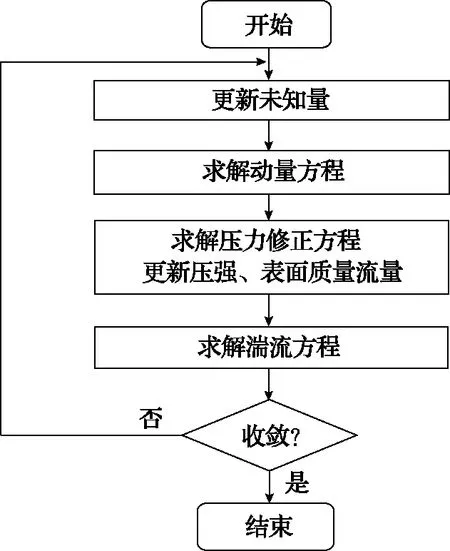
图2 算法流程

1.2.3 定解条件

(1)初始条件。初始条件指t=0时刻，煤样煤层气压力分布情况，即

t=0，x=0～0.1，r=0～0.025：P=0.1×105

式中：x为煤样轴向距离，m；r为煤样径向距离，m；P为煤样操作压力，Pa。

(2)进口边界。进口边界设定为压力进口边界条件，满足：

t>0，x= 0：P=Pi

式中：Pi为入口压力，Pa。

(3)出口边界。出口边界设为压力出口边界条件，表压为0。

(4)壁面边界。对于粘性流体而言，流体将粘附于固体表面，将满足无滑移边界条件。

计算式中的相关物性参数和特性数据见表1[12]。

2 结果与讨论

2.1 计算值与实验值对比

计算过程中煤样密度、孔隙率和吸附常数等采用表1所示物性数据，为了对引入的数学模型和计算条件进行验证(图3)，计算数据采用了与文献[10]寺河矿相同的实验条件，入口煤层气压力设定为：0.3 MPa、0.45 MPa、0.6 MPa、0.75 MPa、0.9 MPa、1.05 MPa、1.2 MPa、1.5 MPa，出口煤层气压力恒定为大气压。

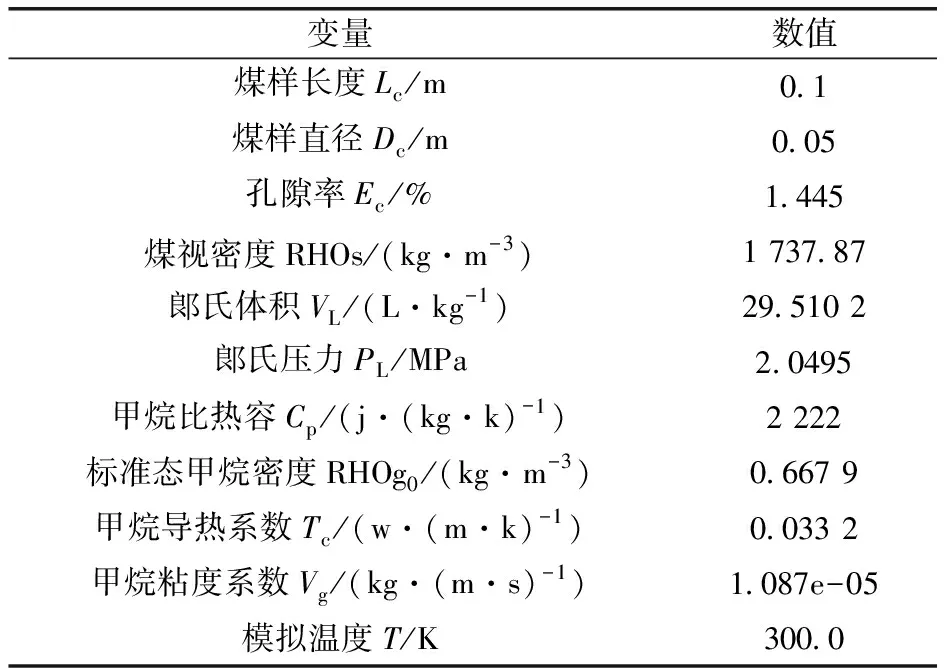
表1 物性数据及相关参数

图3 计算值与实验值在不同进口压力下渗流速度的比较

已考虑质量源项、动量源项与湍流影响的计算值与实验值相比吻合程度高，主要是因为煤层基质收缩渗透率的变化，可从煤样形变角度考虑[10]，建立在分子力学理论基础之上。甲烷分子吸附在煤层表面，导致煤层的表面能下降，煤分子之间的引力减小，间距增大，体积膨胀，渗透率增大，但是当压力逐渐增大时，煤的基质膨胀无法向外释放故向内压缩，故向内压缩，导致煤层渗透率降低，因而出现实验值在压力P=1.5 MPa时明显低于计算值的情形。计算值考虑了瓦斯在渗流过程中，煤样对其吸附及吸附引起渗透率的变化的影响，以及在渗流过程中各项湍流均匀，计算值与实验值的偏差最大为7.08%，出现在压力P=1.5 MPa处。

2.2 压力分布

煤层气在煤层中的流动是一个连续变化的过程，煤层中煤层气压力沿轴向也是一个变化的过程，图4为煤层气压力分布云图。

图4 煤层气压力分布云图

由图4可知，煤层气在煤样中的渗流过程中，入口压力越大，靠近出口处的等压面间距越小，对应的压力梯度越大；在煤样内，等压力表面间距变化不大时，表明压力稳定，梯度变化小，入口压力越高压力梯度越大。煤层中煤层气压力随着煤样轴向距离(x)呈逐渐下降的趋势，最终达到出口处的0.1 MPa。入口压力越大，其对应的压力变化也越剧烈，到达出口位置(x=0.1 m)时，压力变化达到最大。而随着入口压力的减小，煤层气压降趋于稳定。在实际中，煤层气压力越大，出口处压力梯度越大，越容易发生煤层气突出事故。

2.3 轴向速度分布

煤层气在流动中，轴向速度随着压力的降低变化，分析煤层气在不同压力下的速度变化，可对煤层气在不同压力条件下的涌出进行计算和预测。由于煤样对煤层气具有吸附作用，与不考虑吸附相比，轴向速度分布呈现出较大差异。计算时，选取了圆管x=0.02 m，0.04 m，0.06 m，0.08 m，0.1 m处作为考察截面，取r=0的对称面，分析吸附作用下煤层气在煤样中的轴向速度分布。图5为考虑质量源项、动量源项与湍流影响时，不同压力下煤层气在煤样中的轴向速度分布。

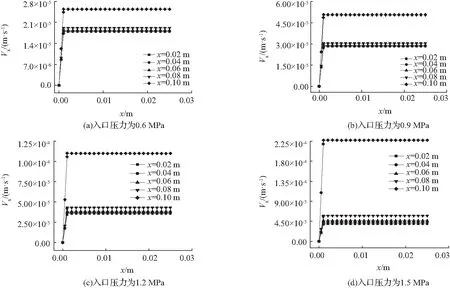
图5 不同压力下煤层气的轴向速度分布

由图5可知，由于煤层气在煤样中的流动属于多孔介质渗流，轴向速度在煤样中分布均匀，壁面处因无滑条件而恒定为0。由于游离煤层气在连通的孔隙和裂隙中产生渗流流动，当压力增加时，煤体内部的裂纹和孔隙闭合减少，煤体内部裂纹得到充分发生和发展，单位时间内通过煤体的煤层气流量增大[9]；而且，由于出口压力恒定为大气压力，随着入口煤层气压力的增加，煤样两端的煤层气压差也越大，煤层气从煤样中渗透的推动力加大，煤样内的煤层气渗流速度也逐渐增加。同时，煤层气沿轴向流动时，由于压力沿轴向降低，煤层气密度变小，体积增大，所以渗流速度沿轴向逐渐增大，由于出口附近压力变化剧烈，速度在压力最低的出口处(x=0.1 m)达到最大值。

3 结 语

煤层气在煤样中的流动属于多孔介质渗流，壁面处因无滑条件而恒定，在建立煤样煤层气流动的数学模型中，考虑质量源项与动量源项的同时，引入了湍流方程，在恒定有效应力和变渗透率的条件下，当入口压力P≤0.9 MPa时，对煤层气在煤中渗流的计算结果与实验数据吻合良好。煤层气在煤样渗流过程中，入口压力越大，靠近出口处的等压面间距越小，对应的压力梯度越大。煤层气沿轴向流动时，由于压力沿轴向降低，煤层气密度变小，体积增大，所以渗流速度沿轴向逐渐增大，由于出口附近压力变化剧烈，速度在压力最低的出口处(x=0.1 m)达到最大值。