基于分解思想的时间序列变量相关关系研究

2022-11-01崔俊富陈金伟

辽宁工业大学学报(社会科学版) 2022年5期

关键词：季节趋势变量

崔俊富,陈金伟

本刊核心层次论文

基于分解思想的时间序列变量相关关系研究

崔俊富1,2,陈金伟3

(1. 南京航空航天大学经济与管理学院，江苏南京 211106；2. 山东女子学院经济学院，山东济南 250300；3. 南京审计大学经济学院，江苏南京 211815)

研究变量之间的相互关系是变量分析的重要内容，相关关系是变量之间重要的相互关系。本文首先将时间序列变量分解成趋势因素、循环因素、季节因素和随机因素四个分解因素；其次构造了分解因素解释力的测算方法，用于反映各分解因素的重要性；最后以年度时间序列变量和月度时间序列变量为例进行了实证研究，测算分解因素的相关系数和解释力。整体来看，基于分解思想的时间序列变量相关关系测度可以得出更加科学有效的结论。

分解思想；时间序列变量；相关关系；解释力

一、引言

从已有变量数据出发，发现变量之间的关系形态及强度，并挖掘内在规律是变量分析的重要内容。在实际经济社会发展中，函数关系和相关关系是较为常见的两种关系。函数关系是比较确定的关系，形如=()，变量和变量的关系由函数(•)确定，变量变化时，通过函数(•)影响变量随之一起变化。由于变量的影响因素很多，某一变量与另一变量的确定函数关系很难找到，于是作为不确定数量关系的相关关系更具有普遍性[1]。相关关系的研究需要解决是否存在相关关系、相关关系的强度如何等问题[2]。通常采用的研究方式是测算相关系数，一般测算Pearson相关系数或Spearman相关系数[3]。Pearson相关系数也称线性相关系数，Spearman相关系数是非参数方法，先对每个变量分别配置，然后求解Pearson相关系数，测算方法如下所示。

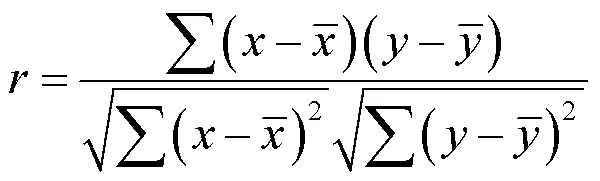
其中，R和R分别为变量和变量的秩，d是秩差。

相关系数测算比较简单，也比较直观，在相关关系研究中应用非常广泛，但是直接测算相关系数是相对粗糙的研究结果[4]。为获得更加全面准确的结果，应该根据不同的变量类型采用不同的研究思想，时间序列变量适用于分解思想。

二、时间序列变量的分解

时间序列变量是比较常见、比较重要的变量类型，这种变量具有四个特点：

一是趋势性（Trend）。绝大多数的经济社会变量要么具有上升趋势，要么具有下降趋势，这种趋势可能是线性的，也可能是非线性的。例如，固定资产投资具有比较明显的上升趋势，而单位GDP能耗具有比较明显的下降趋势。二是循环性，或者称为周期性（Cyclical）。许多经济变量呈现繁荣、衰退交替存在的周期性特点。经济学家对经济周期进行了研究，根据时间长短把经济周期分为3—4年的基钦周期、9—10年的朱格拉周期、20年的库兹涅茨周期、60年的康德拉季耶夫周期。三是季节性（Seasonality）。温度的变化会对人类的生产生活产生比较大的影响，这种影响会在经济变量中得到体现，例如不同地区不同季节的旅游业明显不同[5]。四是随机性，或者称为不规则性（Irregular）。随机性一方面确实是随机因素导致的，无法预测，另一方面是除趋势性、周期性、季节性之外的其他影响因素也归到随机性中。

根据时间序列变量的四个特点，可以将时间序列变量分解成四个分解因素：趋势因素T、循环因素C、季节因素S和随机因素I。分解可以采用加法和乘法两种形式：

Y=T+C+S+I

Y=T×C×S×I

加法模型还发展了对数加法模型和伪加法模型：

lnY=lnT+lnC+lnS+lnI

Y=TC(S+I-1)

分解的方法主要包括CensusX11、CensusX12、移动平均等方法。但是这几种方法只能将时间序列分解成趋势循环因素序列TC、季节因素序列S和随机因素序列I，无法将趋势因素T、循环因素C分离开，分离趋势因素T、循环因素C必须使用Hodrick-Prescott滤波或Band-Press滤波等方法[6]。

三、分解因素的相关关系和解释力

对综合性时间序列变量先进行分解，分解出趋势因素序列T、循环因素序列C、季节因素序列S和随机因素序列I，然后分别讨论各种因素之间的相关性可以得出更加科学有效的结论。另外，各分解因素均含有一部分变量信息，对时间序列变量进行分解之后，可以讨论各分解因素对时间序列变量的解释力[7]。

（一）分解因素相关关系

趋势相关性：具有明确上升趋势或下降趋势的序列之间，趋势因素表现得就非常明显。例如，由经济理论可知，GDP和固定资产投资联系紧密，固定资产投资导致物质资本形成，为GDP的产生提供物质条件，同时以GDP为代表的社会财富是固定资产投资的来源，GDP越高，固定资产投资也越高。因而，对于一个经济体而言，GDP序列和固定资产投资序列就具有非常一致的趋势，特别是高速发展的经济体，趋势因素的关联强度就非常高，其他因素可能就不明显[8]。

循环相关性：经济变量都具有一定的周期性，特别是相互紧密联系的经济指标、经济体之间，经济波动存在一致性。例如，A经济体与B经济体相互经济往来密切，当A经济体经济发展较好时，B经济体受到A经济体的影响，其经济发展动力较强，反之，当A经济体经济发展较弱时，B经济体经济发展也将会受到其影响。于是，两者经济发展周期将呈现一致性，其循环因素的关联强度将比较高[9]。

季节相关性：由季节因素导致的相关性，更多地表现为不同变量受季节因素的影响是否显著，或者两个变量受季节因素的影响是否同步。

不规则相关性：对于平稳的时间序列（趋势性、循环性、季节性都不明显），那么不规则因素的相关性就显得非常重要，如果两个序列不规则相关性很强，那么说明两个变量的联系非常紧密[10]。

四个分解因素对于不同时间序列变量的重要性是不同的，对于某一个具体时间序列变量，可能某一个因素含有的变量信息较多而其他分解因素含有的变量信息较少，此时，研究含有变量信息较多的分解因素的相互关系就是最有参考价值的，其他分解因素的相互关系参考价值较少[11]。另外，测算的所有四个要素的关联强度都在[0,1]之间，这就需要对每个组成部分的关联强度进行有效评价，也就是发现每个分解因素关联强度的解释力大小。

（二）分解因素解释力

线性回归是研究变量之间关系的重要方法，可以用自变量的已知或设定值去估计或预测因变量的均值，对于估计结果的解释力可以使用决定系数来进行判断[12]。对时间序列变量进行分解之后，分别建立原始序列Y与趋势因素序列T、循环因素序列C、季节因素序列S和随机因素序列I的线性回归模型：

可决系数分别为2222，令2=222，可知：

四、实证应用

一般而言，时间序列变量的相关关系都可使用分解思想研究，数据频率越高，变量构成因素越复杂，该思想的结论就越有参考价值。分别以年度时间序列变量和月度时间序列变量为例进行实证讨论。

（一）年度时间序列变量

科学技术是第一生产力，人类的发展进步离不开科学技术的进步。熊彼特认为，创新可以通过引入生产条件和生产要素的“新组合”来建立新的生产函数[14]。SOLOW构建经济增长模型，估算1909－1949年美国人均产出增长大约87.5%来源于科技进步[15]。LUCAS发现，教育和干中学通过促进人力资本积累来推动经济增长[16]。

改革开放以来，中国经济的腾飞离不开科学技术的飞速进步。李翔等认为，科技创新对中国经济的增长具有显著的正效应，实施创新驱动战略有利于中国经济的稳定增长[17]。郑世林等研究发现，1990－2017年科技进步是中国经济增长最重要的动力源泉，年均贡献率高达49%[18]。

专利是重要的科技进步指标，世界知识产权组织数据显示，2019年中国PCT国际专利申请量达到58 990件，已经超越美国提交的57 840件，位居世界第一，与1999年的276件相比，增长了200倍[19]。1995—2019年，中国GDP和专利的变化情况基本是一致的，线性相关系数为0.991，分解之后的趋势因素相关系数为0.996，循环因素相关系数为0.202，见图1和表1。

采用可决系数来测算各分解因素的解释力，对于GDP变量，趋势因素解释力非常高，为95.0%，循环因素解释力较弱，仅为5.0%；对于专利变量，趋势因素解释力非常高，为93.4%，循环因素解释力较弱，仅为6.6%。趋势因素解释力非常高，相关系数为0.996，说明中国GDP和专利相互关系中起决定作用的是趋势因素，也就是GDP和专利的变动趋势是高度一致的[20]。

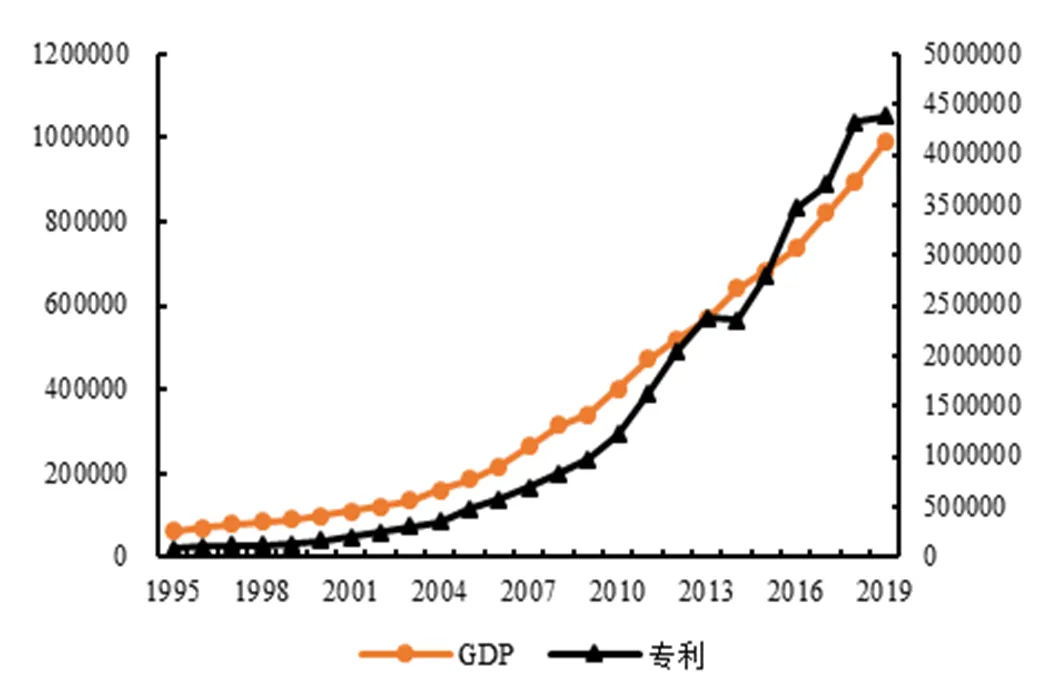
图1 1995—2019年中国GDP和专利

资料来源：国家统计局

（二）月度时间序列变量

价格指数是经济学指标中最重要的指标之一，市场经济最大的作用就是全面、及时、准确地发现价格。

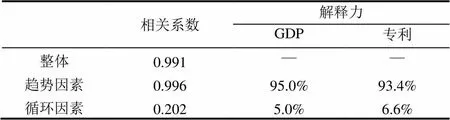
表1 中国GDP和专利分解因素相关系数、解释力

在所有的价格指数中，消费者价格指数CPI（Consumer Price Index）和生产者价格指数PPI（Producer Price Index）应用最为广泛，可以有效反映社会总体物价水平变化和宏观经济运行情况，能够为调控政策的制定提供重要的参考[21]。CPI反映需求端价格变动的趋势与幅度，体现城乡居民消费商品和服务的价格变动情况。PPI反映供给端价格变动的趋势与幅度，体现工业品的出厂价格变动情况[22]。CPI与PPI的联系非常紧密，存在双向作用，涨跌方向和幅度的协同程度较高[23]。2005年1月至2020年12月，中国CPI和PPI的运行情况联系比较密切，线性相关系数为0.542[24]，见图2和表2。

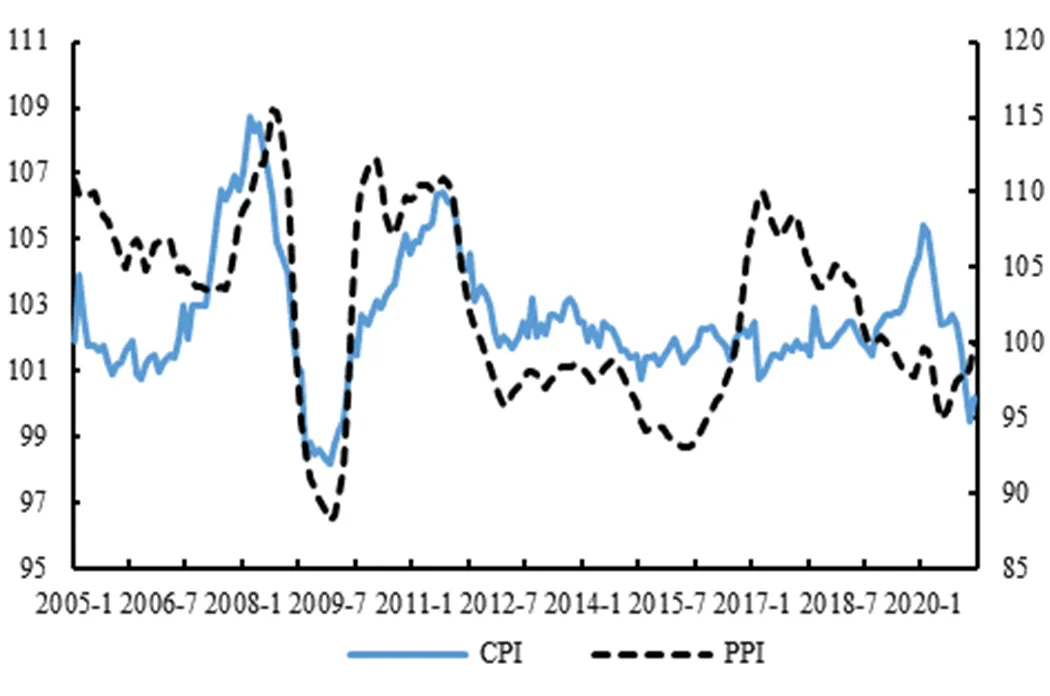
图2 2005年1月—2020年12月中国CPI和PPI

资料来源：国家统计局

将CPI和PPI进行分解，趋势因素、循环因素、季节因素、不规则因素的相关系数分别是0.293、0.681、0.057、0.116。采用可决系数测算各分解因素的解释力。

对于CPI变量，循环因素解释力最强，为67.6%；趋势因素解释力较强，为29.4%；不规则因素和季节因素解释力较弱，分别为3%和0.03%。对于PPI变量，循环因素解释力最强，为56.9%；趋势因素解释力较强，为39%；不规则因素和季节因素解释力较弱，分别为3.9%和0.2%。相对于季节因素和不规则因素，趋势因素和循环因素的解释力比较高，两者解释力之和对CPI和PPI分别为97%和95.9%，相关系数分别为0.293和0.681，说明CPI和PPI相互关系中起决定作用的是趋势因素和循环因素，也就是CPI和PPI的变动趋势和波动周期是基本一致的[25]。

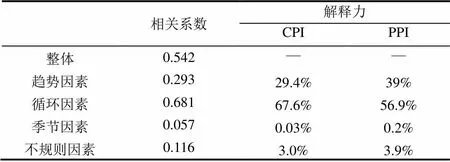
表2 中国CPI和PPI分解因素相关系数、解释力

五、结语

相关关系是研究变量之间相互关系的重要内容，比较常用的研究方式是测算相关系数，一般测算Pearson相关系数或Spearman相关系数。相关系数测算比较简单，也比较直观，但是，相关系数比较粗糙。为获得更加全面准确的结果，应该根据不同的变量类型采用不同的研究思想，时间序列变量适用于分解思想。时间序列变量是比较常见、比较重要的变量类型，该种变量具有趋势性、循环性、季节性、不规则性四个特点，根据其特点可以将时间序列变量分解成趋势因素、循环因素、季节因素和随机因素四个分解因素，分别测算这四个分解因素的相关系数和解释力可以更加全面地反映变量之间的相互关系。本文使用该思想对年度时间序列变量和月度时间序列变量进行了实证研究，得出了更加丰富科学的结论。另外，分解思想不仅仅适用于研究时间序列变量相关关系，还可以推广到计量建模的其他领域。

[1] 郑振龙, 王为宁, 刘杨树. 平均相关系数与系统性风险: 来自中国市场的证据[J]. 经济学(季刊), 2014, 13(3): 1047-1063.

[2] 贾俊平, 何晓群, 金勇进. 统计学[M]. 北京: 中国人民大学出版社,2018.

[3] 威廉·M. 门登霍尔, 特里·L. 辛里奇, 著. 关静, 等, 译. 统计学[M]. 北京: 机械工业出版社, 2018.

[4] 江海峰. 小样本下相关系数的检验与区间估计——基于Bootstrap的研究[J]. 数理统计与管理, 2011, 30(3): 440-446.

[5] 张春华, 高铁梅, 陈飞. 经济时间序列频率转换方法的研究与应用[J]. 统计研究, 2017, 34(2): 92-100.

[6] 高铁梅, 王金明, 陈飞, 等. 计量经济分析方法与建模——EViews应用及案例（第三版）[M]. 北京: 清华大学出版社, 2017.

[7] 吴喜之. 统计学: 从数据到结论(第二版)[M]. 北京: 中国统计出版社, 2006.

[8] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 第四版. 北京: 高等教育出版社, 2008.

[9] 严方笠, 吴建銮. 基于Sieve Bootstrap方法的季节时间序列模型检验问题研究[J]. 数量经济技术经济研究, 2017, 34(7): 124-144.

[10] 吴喜之. 复杂数据统计方法——基于R的应用(第二版)[M]. 北京: 中国人民大学出版社, 2013.

[11] 王群勇. 中国季度GDP的季节调整: 结构时间序列方法[J]. 统计研究, 2011, 28(5): 78-83.

[12] 李子奈, 潘文卿. 计量经济学(第三版)[M]. 北京: 高等教育出版社, 2010.