天基预警雷达低自由度STAP方法研究
2022-11-01段克清李雨凡杨兴家邱梓洲王永良
段克清 李雨凡 杨兴家 邱梓洲 王永良
①(中山大学电子与通信工程学院 深圳 518107)
②(空军预警学院 武汉 430019)
1 引言
天基预警雷达是指以卫星为载荷平台,能对陆、海、空、天中各类运动目标进行远距离探测、定位、跟踪、分类和识别的雷达装备[1-3]。与传统机载预警雷达相比,其探测范围更大、发现距离更远、工作时间更长、探测动目标种类更多,因此是各国未来获取空间、空中及地/海面运动目标信息的重要手段[4-8]。
由于卫星平台高速运动且雷达下视工作,天基预警雷达需要在空时耦合强地/海杂波背景下检测运动目标。因此,如何有效抑制杂波成为天基预警雷达动目标检测需解决的关键问题之一[1-3]。空时自适应处理(Space-Time Adaptive Processing,STAP)技术利用空域和时域联合自适应处理可实现杂波解耦,从而在目标无损失前提下有效滤除杂波,因此是当前各类运动平台雷达实现杂波抑制和运动目标检测的关键技术[9,10]。然而,尽管STAP技术当前已广泛应用于机载预警雷达系统,但当其应用于天基预警雷达时遇到更复杂的问题[1-3]。具体来说,天基预警雷达最大探测距离可达数千公里,为避免过度距离模糊及副瓣杂波电平积累过高,其多工作于中重频[1-5],即便如此距离模糊也较机载预警雷达严重数倍;同时,卫星平台运动速度可达数千米/秒以上,相应杂波多普勒带宽数十倍于机载预警雷达,引起极为严重的多普勒模糊;此外,地球自转等效于给天基预警雷达阵列引入偏航角[11-14],导致各次距离模糊回波多普勒频率存在显著差异性,使得杂波在方位-俯仰-多普勒三维空间呈现紧耦合特性,引起杂波谱特别是主瓣杂波谱在多普勒域严重展宽。上述因素交织在一起,导致传统STAP技术慢速运动目标检测性能严重下降[11-13]。
目前,国内外针对天基预警雷达杂波抑制问题提出了系列解决方法。Kogon等人[15]提出优化重频的方式来减小多普勒模糊和距离模糊影响,但该方法模糊杂波抑制性能提升空间有限。Zulch等人[12]提出理论上可采用动态调整阵列轴向的方案来抵消由地球引入的等效偏航角。然而,一方面由于超大孔径天线轴向角的实时调整不可避免存在误差,且后续STAP方法对该误差非常敏感[12];另一方面也受限于卫星载荷有限的功率支持[16]。因此,该方案并非最优选择,仍需考虑从信号处理级消除由等效偏航角引起的不利影响。此后,Zulch等人[17]又进一步提出在相干脉冲时间内调制发射波形来解耦合,但代价是后续无法解距离模糊。郁文贤等人将经典杂波谱配准法[18]进行了改进,提出频率非均匀采样谱配准法校正天基预警雷达杂波空时谱[19];然而,基于空时平面杂波谱校正的方法仅适用于不存在距离模糊的情况,一旦存在距离模糊,则各类校正方法因无法同时校正各次模糊杂波谱而性能明显下降。此外,该类方法需对各个距离门依次进行校正处理,运算量巨大。
除上述方法外,利用阵列俯仰自由度参与STAP处理可实现方位-俯仰-多普勒三维耦合杂波解耦。Hale等人[20]提出利用天线俯仰自由度可预先滤除俯仰耦合杂波,但仅适用于机载阵列俯仰向杂波松耦合情况,且在实际应用中很难获得各次耦合杂波分量;Corbell等人[21]进一步提出方位-俯仰-多普勒三维(Three-Dimensional,3D) STAP方法,可实现非正侧阵机载雷达三维耦合杂波的解耦,但却并不适于天基预警雷达实际应用。其原因在于:一方面,天基预警雷达阵列方位孔径较大,尽管其副瓣杂波大部分被天线双程低副瓣衰减,但剩余强副瓣杂波由于与主杂波位于较近方位空频,因此需较大方位自由度参与自适应处理才可进一步抑制;另一方面,非正侧阵机载雷达仅近程杂波方位-多普勒谱与其他模糊距离回波谱存在显著差异性,而天基预警雷达由于卫星平台高速运动,即使微小偏航角也导致各次距离模糊杂波方位-多普勒谱均存在显著差异,这就要求较多俯仰自由参与STAP处理。因此,传统3D-STAP方法应用于天基预警雷达杂波抑制时需较多方位和俯仰自由度同时参与自适应处理,所带来的巨大均匀训练样本需求和运算量使其无法适用于实际多变杂波环境且满足星上实时处理需求。降维3D-STAP方法可显著缓解样本需求和运算量负担[22],但由于各子阵杂波分布不一致使其主瓣杂波抑制性能仍存在明显损失。基于深度学习的STAP方法可有效降低快拍需求,能够显著改善副瓣杂波区杂波抑制性能,但却无法从根本上解决三维耦合杂波抑制问题,因此主瓣区杂波抑制性能依旧较差[23]。
针对上述问题,本文首先介绍了平面阵天基预警雷达回波空时信号模型,然后详细分析了天基预警雷达在方位-俯仰-多普勒三维空间的杂波耦合特性,并在此基础上提出基于方位锥削级联俯仰-多普勒自适应处理思路的三维级联STAP (3D Factored STAP,3D-FSTAP)方法,最后通过仿真分析验证了所提方法的有效性。
2 平面阵天基预警雷达杂波信号模型
假定卫星轨道为圆形轨道,天基预警雷达在固定轨道高度H上以恒定速度v绕地球运动。建立右手坐标系XYZ,其中X轴指向卫星惯性运动方向,Z轴指向地心,如图1所示。同时假设天基预警雷达阵列为方位N阵元、俯仰M阵元正侧摆放均匀平面阵。θ和φ分别为天线波束指向当前杂波块的方位角和俯仰角,Rc为雷达与杂波块之间斜距。
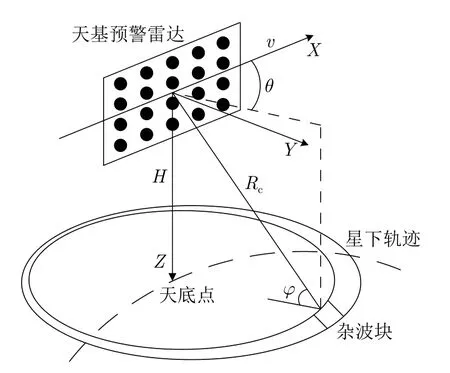
图1 天基预警雷达几何坐标系Fig.1 Space-based early warning radar viewing geometry
受地球自转影响,杂波块对应归一化多普勒频率可表示为[12]
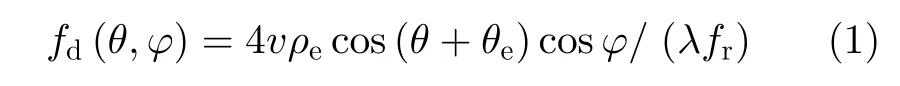
其中,λ为雷达工作波长;fr为脉冲重复频率;ρe和θe分别为由地球自转引起的偏航幅度和偏航角,且仅与卫星轨道倾角和当前所处纬度有关。同时,定义归一化方位空间频率和归一化俯仰空间频率为


其中,K为相干处理时间内脉冲个数,(·)T表示矩阵转置运算。
假定各杂波块统计独立,则任一距离单元杂波空时快拍数据可表示为不同模糊距离上各杂波块回波信号叠加[24]

其中,Na和Nc分别为模糊距离环个数和单个距离环上杂波块个数;ξ(θq,φp)表示第p个模糊距离环上第q个杂波块回波幅度,且与雷达发射功率、天线增益、杂波块反射截面积、地形散射系数和雷达与杂波块间斜距等因素有关;⊗表示矩阵之间的Kronecker积。
由于各杂波块统计独立且ξ(θ,φ)为零均值、方差为(θ,φ)的高斯随机变量,因此该杂波数据相应的杂波协方差矩阵(Clutter Covariance Matrix,CCM)可表示为[24]
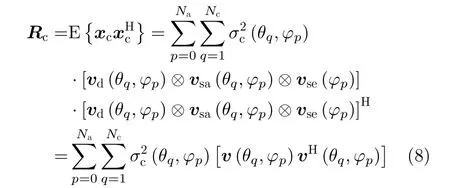
其中,E{·}表 示取期望;(·)H表示矩阵共轭转置运算;v(θ,φ)∈CMNK×1表示杂波块对应空时二维导向矢量。
在保持目标能量基础上最小化输出噪声和杂波功率,可得最优空时二维滤波器权系数

3 天基预警雷达杂波特性分析
地球自转对雷达回波多普勒频率产生影响,等效于引入偏航幅度ρe和偏航角θe[2,3,12]:

其中,ve为赤道上地球自转速度;Re为地球半径;α为星下点纬度;β为轨道倾角。由式(11)可知,当卫星轨道倾角β为0°(赤道轨道)时,其等效偏航角为0;而当卫星轨道倾角β为90°(极地轨道)且星下点纬度α为0°时,可得最大等效偏航角约为3.77°。
考虑等效偏航幅度和偏航角情况下,杂波归一化多普勒频率与归一化空间频率的关系可进一步表示为

其中,fse=2dsin(φ)/λ ≈2d(H/Rc)/λ,即俯仰空频的变化对应回波不同俯仰来向或距离。由式(12)可见:当θe0时,杂波多普勒频率fd、方位空频fsa和俯仰空频fse存在耦合关系。
下面结合斜侧阵机载预警雷达对比分析天基预警雷达杂波分布特性。其中,机载预警雷达参数采用典型装备系统参数,天基预警雷达参数参照美国L波段轻型天基雷达(L-band Lightweight Space Based Radar,LLSBR)计划[3,25],具体见表1。

表1 仿真参数Tab.1 Parameters of simulation
本文杂波谱均由最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)谱[26]估计得到,其数学表达式为P=。图2为方位主瓣杂波距离-多普勒功率谱。其中,图2(a)和图2(b)分别对应斜侧阵机载预警雷达和等效偏航角为3.77o天基预警雷达情况。由图2可以看出,上述两种情况下的杂波均存在距离依赖性或非平稳性。不同的是,由于载机速度相对较慢,机载雷达非平稳杂波仅限于近程不模糊杂波区域,其他中远距各次模糊回波则近似平稳;而天基雷达由于卫星平台速度较快,整个探测距离上杂波多普勒频率均存在显著差异性,导致多次距离模糊后主瓣杂波在多普勒域发生严重展宽,从而在检测运动目标时形成大范围速度盲区。因此,距离模糊和地球自转影响共同作用,使得天基预警雷达主瓣杂波抑制难度大大高于机载预警雷达。

图2 杂波距离-多普勒功率谱Fig.2 Power spectrum of clutter in range-Doppler domain
下面以第250距离门为待检测单元进一步分析杂波分布特性。图3为杂波方位-俯仰-多普勒功率谱。其中,图3(a)和图3(b)分别为斜侧阵机载预警雷达和偏航角为3.77°天基预警雷达两种情况。由图3(a)可以看出,机载预警雷达杂波多普勒频率随方位变化而连续变化,即杂波在方位-多普勒域发生耦合;同时,其多次距离模糊杂波的方位-多普勒谱分布接近一致,仅在不模糊距离对应俯仰空频处的分布显著不同。换句话说,非正侧机载预警雷达杂波方位-多普勒谱仅在大俯仰角来向与俯仰主瓣来向存在显著差异性,因此在方位-俯仰-多普勒三维空间内呈现“松耦合”特性,理论上可利用具有2个俯仰自由度(1个用来抑制俯仰副瓣杂波,1个用来俯仰主瓣保形)的3D-STAP方法实现杂波三维解耦。由图3(b)可以看出,天基预警雷达受天线双程低负瓣衰减影响,其方位-多普勒耦合杂波主要分布于主瓣及高副瓣(如第1副瓣和第2副瓣等)对应方位空频区域,而两者在方位空频上极为接近,需较多方位自由度参与自适应处理才能实现方位-多普勒杂波解耦;同时,该方位-多普勒耦合杂波随俯仰空频连续变化,需较多俯仰自由度参与自适应处理才能实现俯仰-多普勒杂波解耦。因此,天基预警雷达杂波在方位-俯仰-多普勒三维空间内呈现“紧耦合”特性,需较大系统自由度参与自适应处理才能实现三维耦合杂波有效解耦。

图3 杂波方位-俯仰-多普勒功率谱Fig.3 Power spectrum of clutter in azimuth-elevation-Doppler domain
综上所述,与机载预警雷达相比,天基预警雷达杂波分布特性更为复杂。如采用传统2D-STAP处理,则无法实现对其三维耦合杂波的有效抑制;而采用3D-STAP处理,则又需要巨大空域自由度参与,从而导致实际中较难满足的均匀样本需求及不利于星上实时处理的巨大运算负担。
4 3D-FSTAP方法基本原理
由天基预警雷达杂波分布特性可知,其抑制难度在于杂波在方位-俯仰-多普勒的三维紧耦合,因此需设计具有低系统自由度的三维解耦合方法实现杂波有效抑制。在分析天基预警雷达杂波分布内在规律基础上,本文提出了方位锥削级联俯仰-多普勒自适应处理的3D-FSTAP方法。该方法首先通过阵列方位加权抑制方位副瓣杂波;然后再进行阵列俯仰联合多普勒自适应处理,实现对俯仰-多普勒平面耦合的各次距离模糊主杂波解耦处理。下面详细介绍所提3D-FSTAP方法基本原理。
4.1 天基预警雷达副瓣杂波抑制
在天线单元发射功率受器件限制情况下,为获得大功率孔径积实现星上远距离探测,天基预警雷达阵列方位孔径通常远大于机载预警雷达,其平均副瓣电平可低于-50 dB[2,3]。因此,经双程天线副瓣衰减后,绝大部分旁瓣杂波被抑制至噪声电平,剩余杂波分量主要由主瓣杂波和高副瓣杂波组成,且在方位-多普勒域耦合,如图4所示。需要注意的是,为单独分析副瓣杂波对杂波抑制的影响,本节仿真仅考虑等效偏航角为0°的情况。图5给出了传统最优2D-STAP在方位和俯仰自由度分别为8×1,16×1,32×1和64×1这4种情况下信杂噪比(Signalto-Clutter-plus-Noise Ratio,SCNR)损失对比结果。其中,SCNR损失定义为

图4 杂波方位-多普勒功率谱Fig.4 Power spectrum of clutter in azimuth-Doppler domain
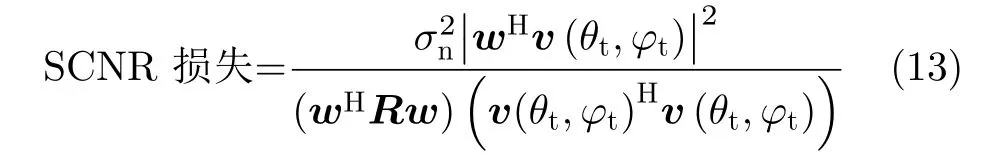
由图5可以看出,副瓣杂波抑制性能随着方位自由度增加而不断提升,且当自由度增至64时,强副瓣杂波区SCNR损失降低至3 dB以内。这是由于阵列方位孔径较大,其方位主瓣和高副瓣分布于较小方位空频范围,因此需要较多方位自由度才能有效分辨主瓣和副瓣杂波,从而实现对杂波方位-多普勒解耦处理。

图5 不同方位自由度SCNR损失曲线对比Fig.5 Comparison of SCNR loss curves with different azimuth degrees of freedom
显然,大系统自由度参与自适应处理所带来的高运算复杂度并不利于星上实时处理。因此需要进一步研究低复杂度副瓣杂波抑制方法。已知天基预警雷达阵列方位孔径较大,可形成远窄于机载预警雷达的方位主瓣(LLSBR计划中法线方向方位3 dB主瓣约为0.26°),其对应方位空频范围占据整个方位空频中极小比例,因此通过有限方位自由度参与STAP处理并不能显著提升主瓣杂波抑制性能,具体如图5所示。换句话说,方位自由度不参与自适应处理并不会带来明显主瓣杂波抑制性能损失。基于该结论,本文提出阵列方位向幅度加权子阵合成单通道来衰减副瓣杂波。已知天线加权可采用发射加权和接收加权两种方式。由于天线发射支路的末级固态放大器工作在饱和状态,其输出功率基本不变,难以满足天线加权函数要求[3],因此采用天线接收加权方式抑制副瓣杂波。此外,考虑到加权导致主瓣展宽损失问题,本文选择可提供最窄主瓣宽度的切比雪夫权系数。下面描述空域加权子阵合成基本原理。考虑空域加权的接收端方位子阵合成矩阵为

加权越深,所引起主瓣展宽越严重。为最小化由加权引起的目标能量损失,本文将加权值设定为各距离门回波数据杂噪比(Clutter-plus-Noise Ratio,CNR)。第l个距离门回波数据杂噪比计算公式为

其中,t r(·)表 示矩阵求迹运算;x=xc+xn∈CNMK×1为雷达接收回波数据,xn∈CNMK×1为高斯白噪声矢量;L为估计CCM所用训练样本数;k为玻尔兹曼常数;T0为基准温度290 K;B为接收机带宽;Fn为噪声系数。
根据表1参数杂波建模,经式(15)计算可得第250距离门CNR为45.6 dB。下面分析采用不同切比雪夫权该距离门STAP处理后的SCNR损失。由图6可以看出,方位不加权时,其副瓣杂波区的强杂波区域存在11~13 dB SCNR损失;而当空域加权至30 dB时,该强副瓣杂波区SCNR损失减小至约6~9 dB;随着加权深度增大,该损失逐渐减小,当空域加权增至50 dB时,该区域SCNR损失减小至约1.7 dB。同时还可看出,采用30 dB,40 dB和50 dB切比雪夫加权分别导致了约1.5 dB,1.6 dB和1.7 dB的旁瓣区固定SCNR损失,这是由主瓣展宽引起的目标损失所致。
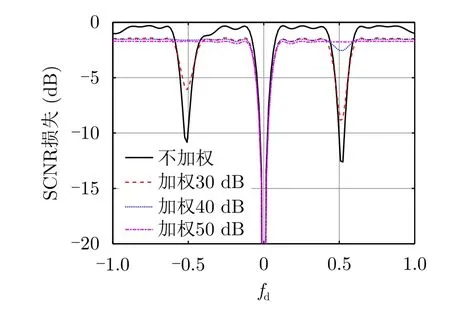
图6 不同切比雪夫权SCNR损失曲线对比Fig.6 Comparison of SCNR loss curves with different Chebyshev weighting
4.2 天基预警雷达主瓣杂波抑制
假设雷达方位零零主瓣对应多普勒带宽为 Δfd,且有Δfd≈2vΔθnn/λ ≈4v/D。其中,Δθnn=2λ/D为零零主瓣宽度,D为阵列方位孔径。如果不考虑地球自转,则可检测目标应处在主杂波多普勒带宽Δfd外,因此对应最小可检测速度(Minimum Detectable Velocity,MDV)为vmin≈Δfdλ/4=λv/D。按照表1中LLSBR参数可计算得到其MDV约为36.5 m/s,可满足天基预警雷达对空中慢速运动目标检测要求。然而,由于地球自转引入了等效偏航角,各次模糊方位主瓣回波多普勒频率存在显著差异性,导致主杂波对应多普勒带宽远大于Δfd。因此,为提高天基预警雷达慢速目标检测能力,需进一步抑制由距离模糊和地球自转共同引起的展宽主瓣杂波。
下面继续以第250距离门数据为例,来进一步分析天基预警雷达方位锥削后杂波分布特性。图7为等效偏航角为3.77°情况下方位副瓣杂波衰减后的MVDR功率谱。可以看出,与图3(b)相比,方位副瓣杂波已被完全消除,杂波在方位-多普勒域上已不存在耦合;同时,剩余杂波分量主要为俯仰-多普勒域耦合的方位主瓣杂波,且该耦合具体表现为杂波多普勒频率随俯仰空频连续变化。因此,需要利用阵列俯仰自由度和时域联合自适应处理来实现主瓣杂波解耦。
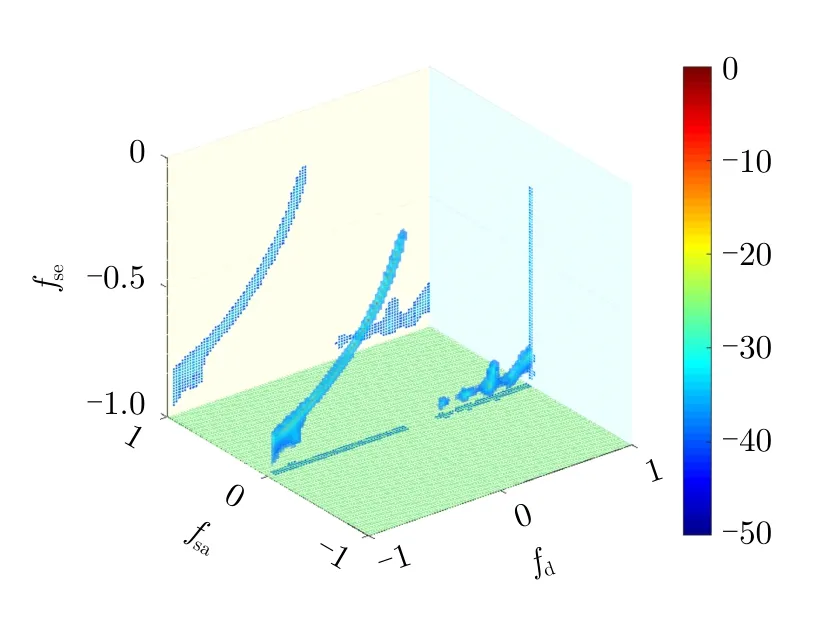
图7 主瓣杂波方位-俯仰-多普勒功率谱Fig.7 Power spectrum of mainlobe clutter in azimuth-elevation-Doppler domain
由于天线阵列俯仰阵元较多,俯仰-多普勒自适应前需要俯仰子阵合成。类似地,接收端俯仰子阵合成矩阵可表示为
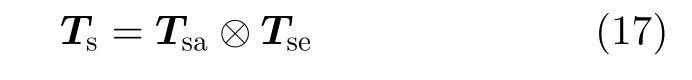
空域合成后,式(9)中空时自适应权可重新表述为

5 仿真分析
本节通过仿真实验验证所提3D-FSTAP方法性能,其中卫星和雷达系统参数见表1。仿真所涉及2D-STAP,3D-STAP和3D-FSTAP方法时域均取全维脉冲参与自适应处理,且待检测距离门设定为第250距离门。
5.1 传统3D-STAP对空域自由度需求分析
本节分析不同空域自由度情况下传统3DSTAP的杂波抑制性能。由于本实验重点对比分析不同自由度对该方法SCNR损失的影响,因此采用最优(Optimum,OPT)空时滤波器进行处理。图8为等效偏航角为3.77o情况下,传统3D-STAP方法在不同空域自由度时杂波抑制SCNR损失曲线对比结果。其中,图8(a)为俯仰自由度为8时,方位自由度分别取8,16,32和64这4种情况SCNR损失结果。可以看出,与图5结果类似,在考虑地球自转情况下,随着方位自由度的不断增加,副瓣区杂波SCNR损失同样逐渐减小,且当方位自由度增至64时,该损失减小至3 dB以内。图8(b)为方位自由度为64时,俯仰自由度分别取1,2,4和8这4种情况SCNR损失结果。可以看出,当俯仰自由度为1时,由于无法实现多次距离模糊杂波在俯仰-多普勒域解耦,导致约二分之一多普勒区域为速度盲区;当俯仰自由度变为2时,增加的一维俯仰自由度可实现对距离模糊杂波的有效抑制,但主瓣区杂波抑制性能依旧欠佳;当俯仰自由度进一步增加时,多余俯仰自由度可进一步削窄俯仰主瓣杂波,从而实现慢速运动检测性能的进一步提升。综上,可看出采用传统3D-STAP处理在较大系统自由度条件下可实现天基预警雷达三维耦合杂波的有效解耦。

图8 不同空域自由度SCNR损失曲线对比Fig.8 Comparison of S CNR loss curves with different spatial degress of freedom
5.2 不同俯仰自由度对3D-FSTAP方法的影响
本节分析俯仰子阵合成通道数对所提3D-FSTAP方法SCNR损失的影响。与5.1节相同,这里仍采用OPT空时滤波器。图9为等效偏航角为3.77°情况下,3D-FSTAP方法取不同俯仰自由度时SCNR损失曲线对比结果。由图9可以看出,与传统3D-STAP方法类似,所提3D-FSTAP方法SCNR损失随俯仰自由度的增加而逐渐减小;当俯仰自由度为2时,该方法可实现对各次模糊主瓣杂波在俯仰-多普勒域的粗解耦,但在主瓣杂波区SCNR损失依旧较大;随着俯仰自由度的增大,其主瓣杂波抑制性能进一步提升,当俯仰自由度增至8时,SCNR损失趋于稳定。

图9 不同俯仰自由度SCNR损失曲线对比Fig.9 Comparison of SCNR loss curves with different elevation degrees of freedom
5.3 不同等效偏航角各方法SCNR损失及MDV性能分析
本节比较2D-STAP,3D-STAP和3D-FSTAP这3种方法在等效偏航角为0°和3.77°情况下的SCNR损失,同时对比各方法对慢速运动目标检测的MDV性能。其中,2D-STAP方法方位和俯仰自由度分别为64和1;3D-STAP方法方位和俯仰自由度分别为64和8;3D-FSTAP方法俯仰自由度为8,方位空域切比雪夫权按照式(15)计算获得。此外,本节重点分析了OPT和对角加载采样协方差矩阵求逆(Loaded Sample Matrix Inversion,LSMI)两种经典空时滤波器。其中,OPT空时滤波器给出各方法性能上界;LSMI空时滤波器采用160个训练样本估计CCM,用来评估CCM矩阵估计误差带来的性能损失。本文LSMI滤波器对角加载量设定为单通道单脉冲上的噪声功率,即
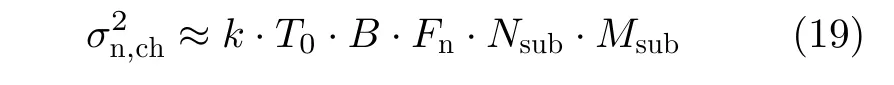
图10为地球自转等效偏航角0°各方法SCNR损失对比结果。其中,图10(a)和图10(b)分别对应OPT和LSMI两类空时滤波器。由图10(a)可以看出,在最优滤波器结构下,2D-STAP和3D-STAP主瓣和副瓣杂波区性能相当,且均在副瓣强杂波区有约1.8 dB性能损失,这是由于方位自由度不足导致副瓣杂波抑制不充分;3D-FSTAP主瓣杂波区性能与上述两种方法相当,但由于加权引起主瓣展宽,其副瓣杂波区均存在约1.7 dB的SCNR损失。由图10(b)可以看出,在LSMI空时滤波结构下,3种方法主瓣区杂波抑制性能与最优方法相当;2D-STAP在旁瓣强杂波区存在3~6 dB的SCNR损失,同时3D-STAP在旁瓣强杂波区损失增至约3 dB,这些均由CCM估计误差所致;需要注意的是,3D-FSTAP方法副瓣杂波区与最优滤波器性能相当。

图10 偏航角0°情况各方法SCNR损失曲线对比Fig.10 Comparison of SCNR loss curves with different methods when crab angle is 0°
图11为地球自转等效偏航角3.77°情况下各方法SCNR损失对比结果。其中,图11(a)和图11(b)分别为OPT和LSMI两类空时滤波器结构。由图11(a)可看出,即使采用最优滤波器,2D-STAP方法SCNR损失依旧较大,从而导致较大目标检测速度盲区;其原因在于2D-STAP无法实现天基预警雷达三维耦合杂波的解耦,使其各次距离模糊主瓣杂波无法有效抑制。而3D-STAP和3D-FSTAP方法由于利用了阵列俯仰维信息,因此在主瓣杂波区SCNR损失显著优于2D-STAP方法。由图11(b)可以看出,采用LSMI空时滤波器时,2D-STAP方法由于CCM估计引入误差,其SCNR损失进一步增大;3D-STAP和3D-FSTAP方法杂波抑制性能与最优滤波器相当,仅前者在副瓣强杂波区损失略有增大。

图11 偏航角3.77°情况各方法SCNR损失曲线对比Fig.11 Comparison of SCNR loss curves with different methods when crab angle is 3.77°
下面结合图10和图11进一步分析偏航角取最小值0°和最大值3.77°两种极端情况下的运动目标MDV性能。其中,0°情况代表了本文仿真条件下天基预警雷达动目标检测MDV性能上界,而3.77°情况则为最恶劣条件下MDV性能下界,其他等效偏航角所对应MDV应位于两者之间。本文采用允许输出SCNR损失为5 dB可检测目标来计算相应MDV[2,3,27],如表2所示。当偏航角为0°时,2D-STAP和3D-STAP在两类滤波器中MDV均约为11.42 m/s;而所提3D-FSTAP由于未在方位向进行自适应处理,其MDV性能略有下降,约为13.33 m/s。当偏航角为3.77°时,2D-STAP在两类滤波器下MDV分别为142.86 m/s和192.35 m/s,远未达到LLSBR所设定42 m/s的MDV指标[3,25];3D-STAP在两类滤波器MDV均可达约15.24 m/s,而3D-FSTAP性能略差,在两类滤波器下MDV均可达约19.04 m/s。需要注意的是,偏航角0°情况下各算法和偏航角3.77°情况下3D-STAP和3D-FSTAP算法MDV性能远优于4.2节中由零零主瓣宽度所估算36.5 m/s指标,这是由于本节考虑了5 dB的SCNR损失容忍度;如果将该容忍度降低到3 dB,则3DLSMI-FSTAP的MDV性能下降为28.57 m/s;如果将该容忍度降低到2 dB,则3D-LSMI-FSTAP的MDV性能进一步下降为45.72 m/s。

表2 MDV性能Tab.2 Performance of MDV
5.4 不同方法距离-多普勒SCNR损失对比
本节对偏航角3.77°情况下所有距离门数据进行杂波抑制处理,以验证所提3D-FSTAP方法在全距离维处理的有效性。同时,给出传统2D-STAP方法在全距离维SCNR损失作为对比。2D-STAP和3D-FSTAP均采用LSMI空时滤波器,其算法参数设定同5.3节,且3D-FSTAP各距离门方位切比雪夫加权系数依照式(15)计算获得。
图12为杂波抑制后各距离门SCNR损失图。其中,图12(a)和图12(b)分别对应2D-STAP和3DFSTAP两种方法。由图12(a)可以看出,在偏航角3.77°情况下,采用传统2D-STAP方法在整个探测距离上均存在较大SCNR损失,导致约一半以上多普勒域无法有效检测运动目标,因此远远无法满足天基预警雷达动目标探测需求;而采用所提3DFSTAP方法仅利用8个空域自由度参与STAP处理,即可在全距离域实现主瓣和副瓣杂波的有效抑制,相较于传统2D-STAP方法SCNR性能大幅提升。

图12 各距离门SCNR损失比较Fig.12 Comparison of SCNR loss of all range gates
5.5 算法收敛性和运算复杂度对比
由上述实验结果可知,3D-STAP和本文所提3D-FSTAP方法均可实现天基预警雷达杂波三维解耦,因此杂波抑制性能较传统2D-STAP方法大幅提升。本节进一步分析比较3D-STAP和3D-FSTAP的算法收敛性和运算复杂度。仿真中,两种方法均采用LSMI空时滤波器,其收敛性对比部分仿真参数设定同5.3节。
本节采用不同训练样本条件下平均SCNR损失性能来评估方法收敛性能。其中,平均SCNR损失定义为所有多普勒通道SCNR损失取平均值。图13为3D-STAP和3D-FSTAP方法采用不同训练样本时SCNR损失曲线对比结果。由图13可以看出,传统3D-STAP收敛速度较慢,需要约140以上训练样本才达到稳定平均SCNR损失;而所提3D-FSTAP收敛性显著优于3D-STAP,仅需约20个训练样本即可实现SCNR损失性能收敛。此外,当样本数足够多时,3D-FSTAP算法平均SCNR损失略低于3D-STAP方法,这是由于前者加权导致固定目标能量损失。

图13 各方法收敛性比较Fig.13 Comparison of the convergence with different methods
本节采用乘法次数来评估各方法运算复杂度。表3为3D-STAP和3D-FSTAP运算复杂度比较结果。其中,L1和L2分别为这两种方法所采用的训练样本数。由上述分析可知,传统3D-STAP方法需较大方位自由度参与自适应处理才能实现次最优杂波抑制性能,因此该方法运算量受方位自由度影响较大。而所提3D-FSTAP方法在CCM估计和空时权系数计算环节运算量均与阵列方位自由度无关,因此其运算复杂度远小于3D-STAP方法,具体如表3所示。

表3 运算复杂度比较Tab.3 Comparison of computational complexity
为更直观地比较上述两种方法运算复杂度,本文给出了不同Ms和Ns情况下的运算量比较结果。其中,L1和L2分别取140和20。图14为两种方法运算量比较结果。其中,图14(a)为方位自由度Ns取64时不同俯仰自由度情况下运算量对比。可以看出,无论Ms取值如何,传统3D-STAP方法运算量均远大于所提3D-FSTAP方法,前者运算量比后者高5个量级以上。图14(b)为俯仰自由度Ms取8时不同方位自由度情况下运算量对比。可以看出,由于所提3D-FSTAP方法运算量计算不涉及方位自由度,因此其乘法次数始终保持在约106量级。不同的是,传统3D-STAP方法运算量随Ns增加而迅速增长;当Ns增至64时,3D-STAP运算量较3D-FSTAP高5个量级以上;当Ns增至128时,前者较后者高6个量级以上。
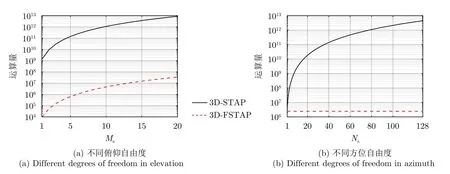
图14 各方法运算量比较Fig.14 Comparison of computational load with different methods
6 结语
由于存在距离模糊和地球自转引入偏航角,天基预警雷达杂波在方位-俯仰-多普勒三维空间呈现紧耦合特性,使得传统方位-多普勒2D-STAP方法杂波抑制性能严重下降甚至失效。基于杂波特性分析,本文认为采用方位-俯仰-多普勒3D-STAP可实现对上述耦合杂波的三维解耦。然而,由于高副瓣杂波和主瓣杂波在方位空频上难以分辨,以及各次距离模糊主瓣杂波多普勒频率随俯仰空频连续变化,要求3D-STAP方法必须采用大系统自由度才能实现杂波有效抑制,从而难以应用于实际。针对上述问题,本文提出了方位锥削级联俯仰-多普勒自适应处理的3D-FSTAP方法,通过两级处理依次完成方位-多普勒和俯仰-多普勒杂波解耦,在确保次最优杂波抑制性能的同时大幅降低了运算量和均匀样本需求,因此可用于解决当前天基预警雷达系统杂波抑制难题。所提方法简单、有效,不仅适用于天基运动平台雷达动目标检测,还可广泛应用于其他各类超高速运动平台。
