杂波背景下的时距联合检测前聚焦方法研究
2022-11-01裴家正陈小龙陈宝欣
关 键 裴家正 黄 勇 陈小龙 陈宝欣
①(海军航空大学 烟台 264000)
②(92337部队 大连 116000)
1 引言
无人机、高机动性隐身战机在内的新一代高速飞行器以及战术导弹、巡航导弹等典型低可观测目标给雷达目标检测带来了较大困难[1]。为了提高雷达对此类高速微弱目标的探测能力,我们通常增加观测时间并通过相参积累来提高目标积累增益,但延长观测时间会存在目标跨距离走动的情况,从而导致经典自适应检测方法对目标的聚焦和检测能力的降低[2]。
采用长时间相参积累是探测跨距离走动的低可观测目标的有效方法之一。目前,国内外涌现出许多优异的长时间相参积累处理方法,Keystone变换(Keystone Transform,KT)类方法便是一类经典的长时间相参积累方法,其通过对慢时间维进行尺度变换能够实现跨距离走动校正[3,4],文献[5,6]基于KT的级联处理方案,对目标速度引起的跨距离走动、目标加速度引起的多普勒谱展宽和更高阶运动参数的影响进行逐级地校正。不过此类方法无法解决多普勒模糊的问题[7,8],同时文献[2]经过实验表明KT类方法会影响杂波功率谱展宽和畸变,导致后续自适应处理算法难以获得最大的输出信杂噪比(Signal-to-Clutter-Noise Ratio,SCNR)。
另外,许稼教授提出的检测前聚焦(Focus-Before-Detect,FBD)类方法较有代表性。此类方法以Radon傅里叶变换[9-11]为基础,其主要思想是通过多维度联合相参积累将长时间相参积累的问题转换为参数化运动模板的匹配问题。通过联合补偿距离走动和多普勒起伏得到的相参积累结果,FBD类方法可在对应的参数空间中形成目标的多维聚焦图像[12,13]。新体制雷达在获取阵元-脉冲-多普勒的空时信号后,通过空时频的FBD处理(Space-Time-Frequency-FBD,STF-FBD)来完成信号的多维联合相参积累[14,15],获得理想的信噪比增益。在此之后,陈小龙等人[16,17]考虑了加速度引起的多普勒谱展宽,提出了基于Radon分数阶傅里叶变换(Radon-FRactional Fourier Transform,RFRFT)和基于Radon线性正则变换的相参积累方法,主要用于海杂波中的机动目标和微动目标检测。
目标的低可观测性不仅与目标自身特性有关,而且与环境有关[18]。RFT方法在高斯白噪声背景下对运动目标具有极好的聚焦性能,然而对杂波的抑制能力有限。雷达自适应处理方法可在目标信号完成相参积累的同时对杂波进行有效抑制,显著提高了系统对SCNR的改善性能[19]。经典自适应处理要求目标信号集中在固定距离单元内,限制了其有效积累时间。为此,许稼团队[20]针对均匀强杂波环境下跨距离走动目标的自适应检测问题,提出了一种自适应Radon傅里叶变换(Adaptive Radon-Fourier Transform,ARFT)方法,可同时实现跨距离走动目标的相参积累和杂波的自适应抑制,能够最大化输出SCNR;并在ARFT方法基础上提出了一种子孔径实现形式降低算法运算量。文献[21]也考虑了均匀高斯杂波背景下的自适应广义RFT (Generalized RFT,GRFT)方法,并推导了参数估计的克拉默-拉奥下限,其本质与ARFT方法相同。文献[22]将参数空间划分为子空间后再利用ARFT方法,并通过增加子孔径的长度平衡计算量和检测性能。
以上研究基于理想脉冲压缩结果得到了较好的效果。而传统级联信号处理流程并不适合高速目标,如果以线性调频为发射信号波形,因不可忽略的脉内多普勒频移,高速目标的脉冲压缩结果中会存在主瓣偏移问题;对于其他复杂波形,除主瓣偏移外还有可能伴随主瓣展宽、主瓣幅度降低等问题[23],不利于杂波背景下目标能量聚焦与信杂噪比改善。
为此,本文按照多维联合检测前聚焦中时(慢时间)-距(快时间)联合的思想,提出了一种将脉冲压缩、RFT与自适应杂波抑制相结合的时距联合检测前聚焦方法(Adaptive-Pulse Compression Radon-Fourier Transform,A-PCRFT)。该方法通过脉冲压缩和RFT的时距两维联合处理,在脉冲压缩前就实现从协方差矩阵未知的高斯杂波背景中对未知跨距离单元走动效应的目标进行检测前聚焦。具体地,方法首先将未进行脉冲压缩处理的相参脉冲串回波数据分为两组,即主数据和辅助数据。辅助数据中只包含独立同分布的杂波和噪声,利用该数据作为训练样本,通过其最大似然估计来替代主数据所用到的杂波协方差矩阵。然后,根据脉冲压缩前得到的杂波协方差矩阵以及在距离-速度参数空间中得到的二维导向矢量,得出最优滤波器权矢量,完成自适应杂波抑制。实验表明,A-PCRFT方法能够避免级联处理中的主瓣偏移等问题,而且聚焦性能优于ARFT方法。
2 问题建模
假设雷达发射脉冲内共有N个点,N=Tp·fs,Tp是脉宽,fs是采样频率。脉冲波形用s表示,s=[s(0),s(1),...,s(N -1)]T。
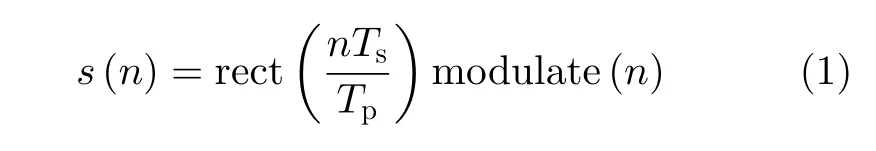
其中,Ts=1/fs是采样时间间隔;0 ≤n ≤N-1;rect(·)为矩形窗;modulate(·)为脉冲信号的调制形式,基本为线性调频形式。
2.1 信号模型
为方便说明问题,假设场景中存在单个目标,在有限的积累时间内目标的高阶运动尚不明显,只考虑速度。设置t为慢时间变量,目标与雷达之间的瞬时距离r(t)与运动参数(rT,vT)有关,
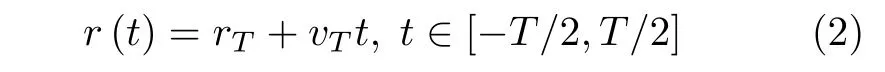
其中,rT是目标0时刻的距离,vT是目标速度,T是相参积累时间。接收信号在距离-脉冲(即r-t)平面如图1所示,单位分别为m和s。考虑到目标的跨距离走动,相参脉冲串处理数据被分为两部分:一部分为搜索区域,另一部分为数据提取区域[23],搜索区域包含在数据提取区域之中。在处理数据的中心记为rC,目标的初始距离和速度未知,因此需要在距离搜索区间[rC-ra/2,rC+ra/2]和速度搜索区间[-vmax,vmax]进行搜索,ra代表目标0时刻可能位于的距离范围,vmax是设定的最大速度。rg=ra+vmaxT,代表T内目标通过走动可能经过的所有距离范围。图1为脉冲压缩前参数搜索与数据提取范围示意图,图中给定有3个目标,其运动参数分别为(rC,vT),(rC-ra/2,-vmax)和(rC+ra/2,vmax)。
[rC-ra/2,rC+ra/2]为搜索区域的范围,距离分辨率Δr=c/(2fs),c是光速,Nr=ra/Δr为搜索区域内距离单元的总数。由于是脉冲压缩前的数据,图1中的目标回波是一条宽度为N的斜条而不是斜线,因此数据提取区域还需要在rC+rg/2后沿距离增大的方向延伸(N-1)Δr的长度,所以数据提取区域的范围为[rC-rg/2,rC+rg/2+(N -1)Δr]。Ng=rg/Δr,于是Ng+(N-1)为数据提取区域内距离单元的总数。设TPRI是脉冲重复间隔(Pulse Repetition Interval,PRI),T内共Np个相参脉冲的回波数据,Np=T/TPRI。假设目标脉间不起伏,在下变频和模数转换后,脉冲压缩前第m个PRI (1≤m≤Np)中目标的回波矢量目标信号的离散模型可表示为
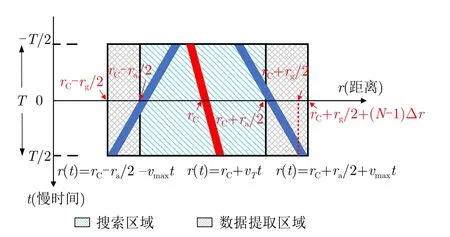
图1 PC-RFT方法的参数搜索与数据提取区域Fig.1 Parameter search and data extraction area of PC-RFT

脉冲回波包含杂波和噪声,因此脉冲压缩前回波信号应重写为

2.2 结合脉冲压缩和RFT的PC-RFT方法
高速目标回波的脉内多普勒频率不可忽略必须考虑在内,脉冲压缩和RFT结合的PC-RFT方法是根据目标的参数rT和vT将其回波能量逐脉冲、逐距离单元地进行二维积累。Np维慢时间矢量不适合作为目标的导向矢量,而需要用时距联合利用波形和多普勒共同构建目标的导向矢量。由于目标参数rT和vT都是未知的,且搜索数据中可能存在多个目标,因此参数空间需要全部网格化搜索。虽然速度参数取值限制在[-vmax,vmax],但速度的遍历搜索较为复杂,需要用长度为Δv=λ/(2T)的速度网格对速度搜索区间离散化[24,25],则速度维需要遍历Nv=round(2vmax/Δv)个网格单元。根据目标的距离搜索区间和雷达回波数据的采样情况,距离按照长度为Δr的距离网格对距离搜索区间离散化,则距离维需要遍历Nr个网格单元。PC-RFT的离散形式可表示为[23]
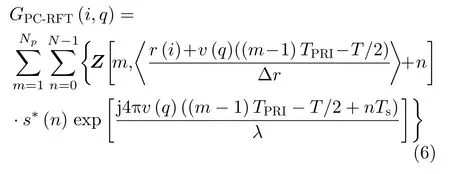
其中,Z为式(5)中的回波。i(1≤i≤Nr)和q(1≤q≤Nv)分别指代距离维和速度维网格变量,r(i)=rC-ra/2+iΔr,v(q)=-vmax+qΔv。但由于这样的遍历搜索针对没有杂波的场景,在杂波背景下杂波的能量也会被积累,因此方法性能会受到较大影响。
3 A-PCRFT方法设计
A-PCRFT方法实现的时距联合检测前聚焦在脉冲压缩和RFT结合的基础上加入自适应杂波抑制。
按照图2,A-PCRFT方法的基本流程分为以下步骤:
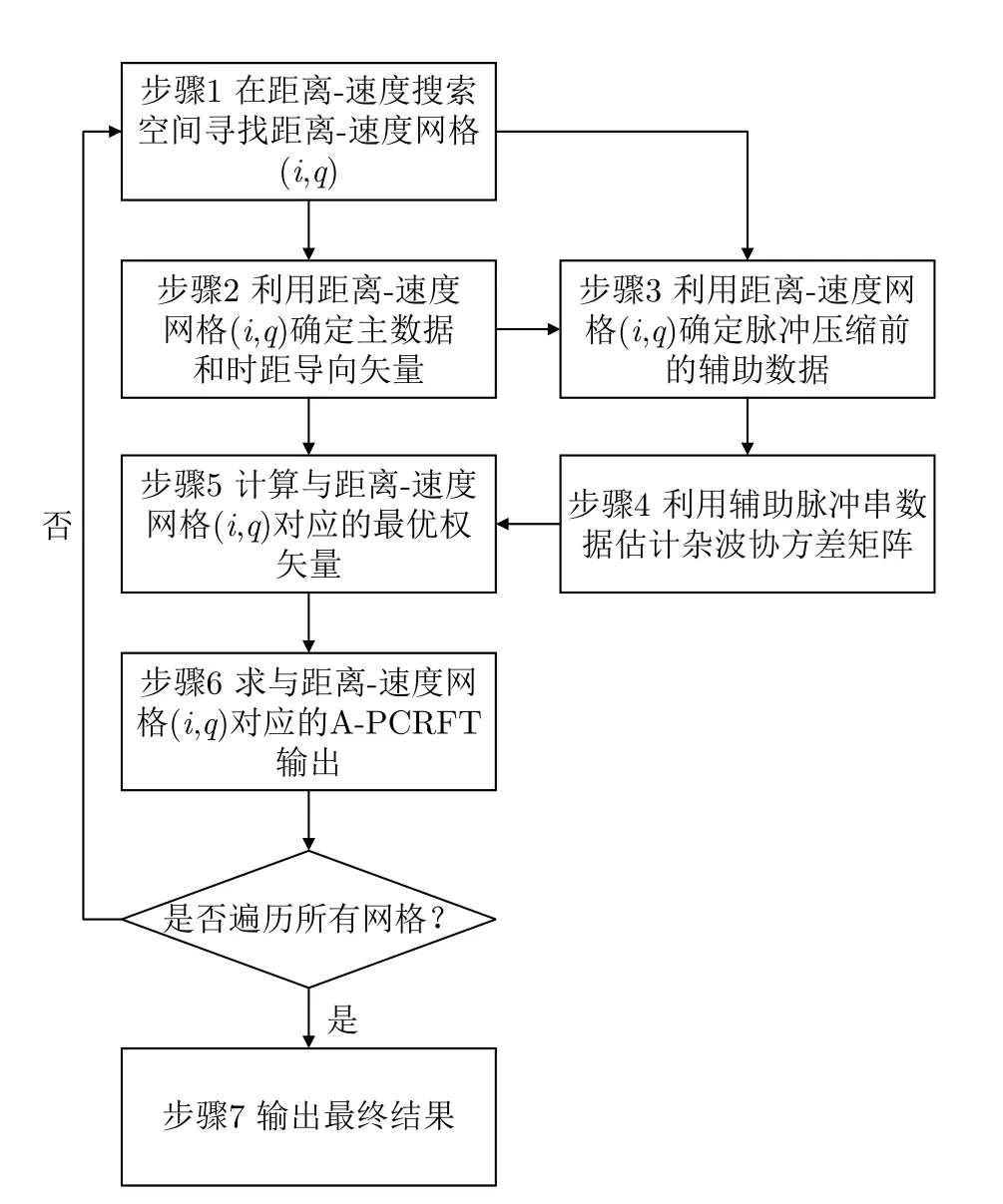
图2 A-PCRFT方法的流程图Fig.2 Flow chart of A-PCRFT method
步骤1 从第2节描述的距离-速度搜索空间中寻找第i个距离单元与第q个速度单元确定的距离-速度网格(i,q)。
步骤2 利用距离-速度网格(i,q)在图1中的脉冲串数据内确定该网格对应的主数据和时距导向矢量。
图3中蓝色区域为包含有目标回波信号的主数据,目标回波在主数据之中由黄色圆形标出。主数据记为ZP,表示为

图3 A-PCRFT方法所需要处理的数据Fig.3 Schematic diagram of data required in A-PCRFT method
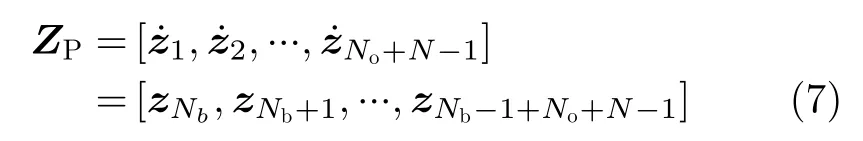
其中,No=v(q)T/Δr是目标在T时间内跨过的距离单元数,主数据的距离单元总数为No+N -1。Nb是目标在积累时间中距离单元的最小值。网格(i,q)中的i也在图3中标出,为0时刻目标所在距离单元的位置。主数据还可表示为


当杂波的时间和空间分布缓慢变化时,可用相同的辅助数据。
步骤4 利用辅助脉冲串数据估计杂波协方差矩阵。文献[19]中的回波模型要求式(8)中No=1,而且默认为脉冲压缩后的数据。而此处为最大化输出跨距离走动目标的SCNR,首先需要将主数据矢量化表示
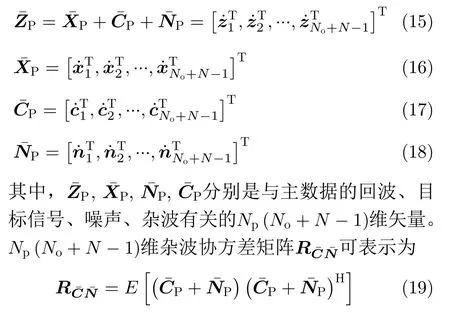
(·)H为共轭转置运算,协方差矩阵需要从辅助数据中的NS个采样中通过样本协方差矩阵(Sample Covariance Matrix,SCM)估计得到。假设整个观测数据中不同噪声采样都是统计独立的,不同距离单元的杂波也是统计独立的,且杂波在脉内不起伏。基于此假设,所提算法只需要考虑脉间杂波抑制,而不必考虑脉内杂波抑制,便可将的估计值近似为分块对角矩阵。

步骤5 A-PCRFT方法使RFT与脉冲压缩同时进行,仍具有与文献[26]中相似的信号模型表达式。由此可得Np×(No+N -1)维 最优滤波器,即有限冲激响应滤波器系数为
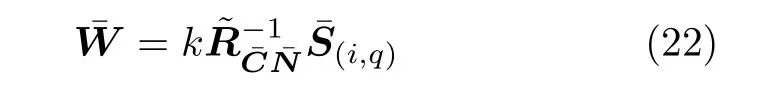
其中,k是一常数。将式(8)和(21)代入式(22)可近似得
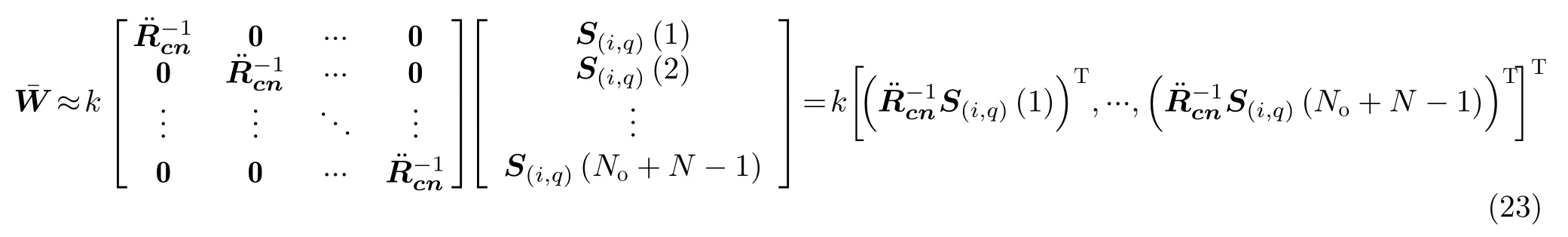
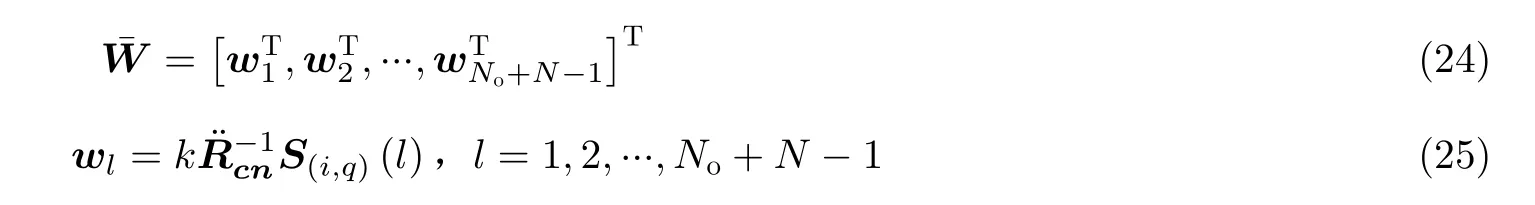
步骤6 由步骤5得该滤波器的输出为

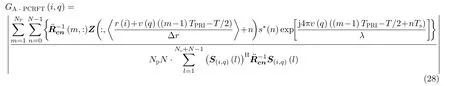
步骤7 最终遍历距离-速度搜索空间内的所有距离-速度网格,即可输出最终结果。
A-PCRFT既采用了与跨距离单元走动补偿类似的相参积累,又直接从辅助数据估计杂波协方差矩阵,实现在时距两维相参积累的同时有效抑制杂波。
4 算法分析
4.1 计算成本分析
本节对算法运算量做出简要分析。首先已知RFT算法的运算量[9,11]为NrNv[NpIm,c+(Np-1)Ia,c],其中NrNv表示对距离、速度的二维搜索,NpIm,c+(Np-1)Ia,c表示的是距离和速度搜索单元确定的情况下在PRI内的累加运算量,Im,c表示复数乘法,Ia,c表示复数加法。脉冲压缩和RFT结合的PC-RFT算法一共需要NrNv(Np-1)Ia,c[N2Im,c+(N-1)Ia,c]的运算量[23]。
A-PCRFT方法计算流程与ARFT方法相似,A-PCRFT方法在能量积累加入了脉冲压缩的部分。其主要步骤包括SCM计算、协方差矩阵求逆及脉内和脉间的能量积累,其中SCM计算成本为NSm,c+NS(Np-1)Ia,c,矩阵求逆的计算成本为(/3)Im,c[20]。按照式(26),脉内和脉间能量积累的计算成本为NrNv{[(No+N-1)+Np]Im,c+[(No+N-1)Np+1](Np-1)Ia,c}。由此可见,A-PCRFT方法联合处理的运算量确实要高于先脉冲压缩后ARFT方法这样级联处理的运算量。
4.2 输出信杂噪比分析
假设针对相同的距离-速度网格(i,q),同等条件下ARFT方法的计算[20]可改写为

其中,ZPC为经过脉冲压缩后的回波脉冲串数据,为单个距离单元脉冲压缩后的杂波协方差矩阵估计,k赋值的准则同式(28),此处不再赘述。
对比式(28)和式(29),可见A-PCRFT方法中不仅用协方差矩阵进行杂波抑制,还对脉内多普勒进行补偿,所以理论上更优。A-PCRFT方法处理后,目标平均功率为
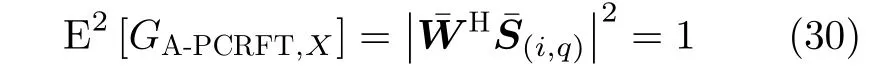
同时,A-PCRFT方法处理后杂波加噪声的平均功率为
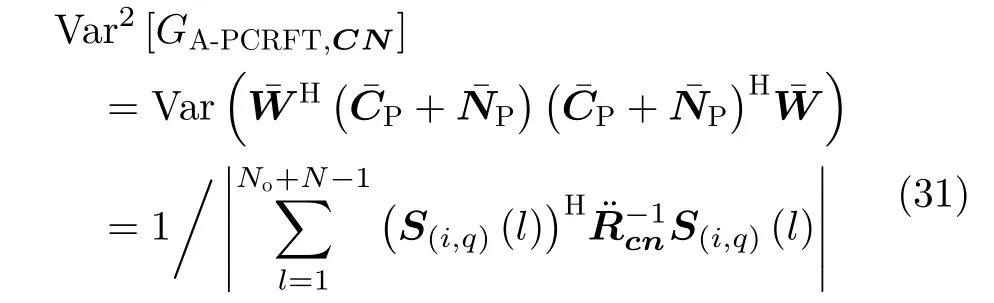
因此,距离-速度网格(i,q)的信杂噪比输出
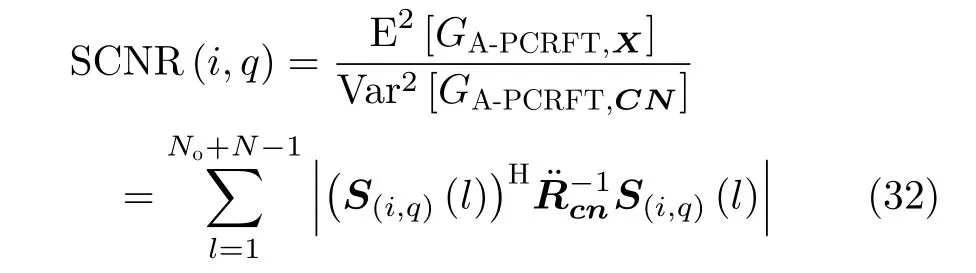
5 实验验证
本节介绍了一些数值仿真实验,以证明所提出的A-PCRFT方法的有效性。实验中假设背景为均匀杂波,其幅度服从高斯分布,多普勒频谱密度函数为高斯谱。雷达系统参数具体为:载频为1 GHz,脉冲重复频率PRF=1000 Hz,线性调频信号带宽6 MHz,脉宽50 µs,采样频率fs=12 MHz (N=600),相参积累时间T=0.3 s (Np为300),杂波频谱中心设置为0 Hz,速度方差为1.5 m/s,即杂波频谱宽度为10 Hz。
本实验将低可观测的运动目标置于场景中心rT=rC(场景中心rC=50 km),其以vT=510 m/s的径向速度远离(多普勒频率为3400 Hz),vmax=600 m/s,搜索区域的距离范围ra=600 m,rg=780 m。Δr=12.5 m,Nr=48,Δv=0.5 m/s,Nv=1200。在脉冲压缩前,目标的SCNR为-25 dB。
脉冲压缩后再进行动目标检测(Moving Target Detection,MTD)后的输出如图4所示。由于MTD的多普勒范围为[-PRF/2,PRF/2]且实验中波长设置为0.3 m,图4根据多普勒频率与径向速度的关系,速度范围为[-75 m/s,75 m/s]。由于跨距离单元走动的影响,经过傅里叶变换后目标能量并没有聚焦于一处,而是分散在同一速度的若干距离单元中,与杂波相比较弱。
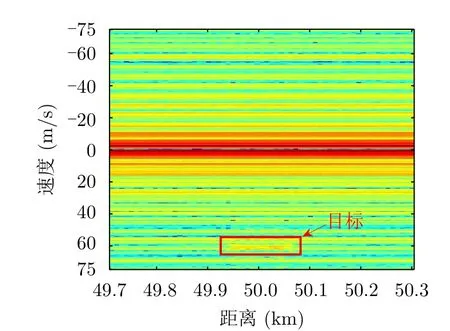
图4 MTD输出Fig.4 Output of MTD
RFT与PC-RFT[23]的输出结果如图5所示,尽管RFT与PC-RFT可以有效积累跨距离单元走动目标的能量,但背景杂波也得到积累,可能会影响目标检测性能。由于将脉冲压缩和RFT结合的PC-RFT方法补偿了脉内多普勒,多普勒频率为3400 Hz的目标主瓣并没有发生偏移。但RFT由于是在脉冲压缩的结果之后进行处理,无法补偿脉内多普勒,目标主瓣产生偏移,从而在发射信号为线性调频信号的情况下,图6中RFT与PC-RFT的目标速度切片稍有不同。若是其他波形,将会产生其他更严重的影响[23]。
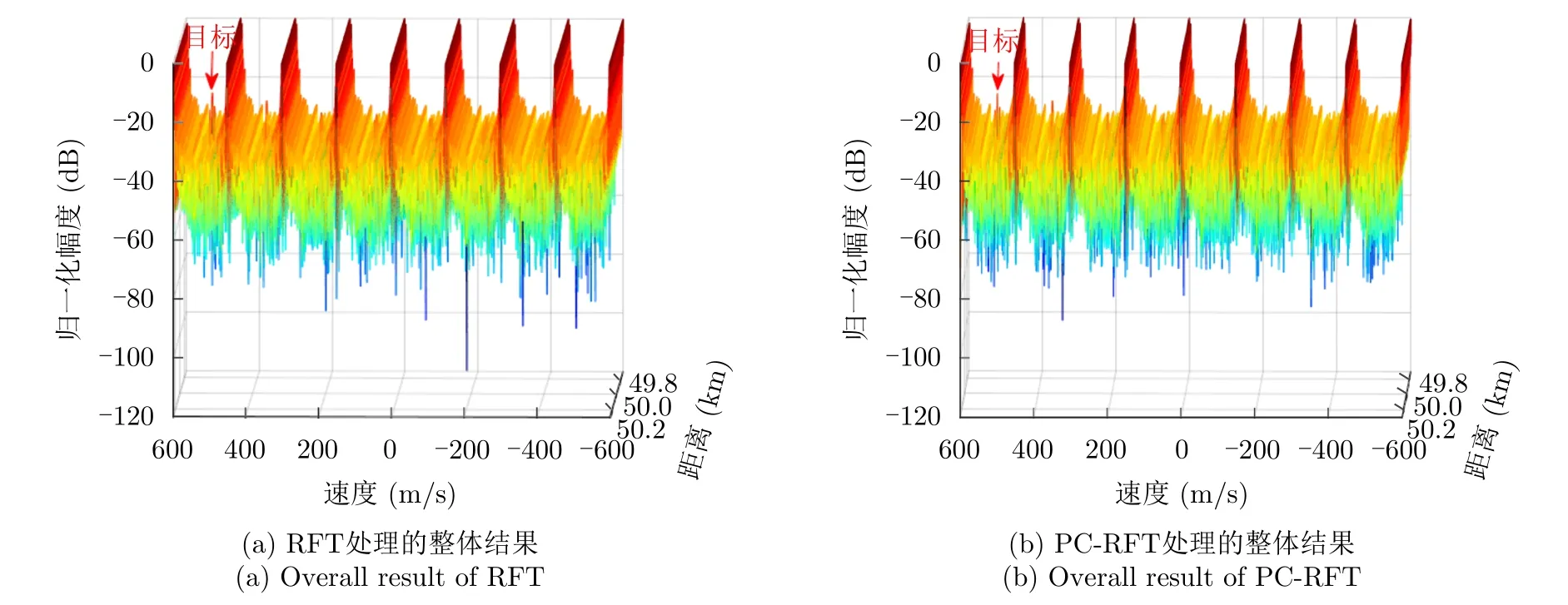
图5 RFT和PC-RFT的处理结果Fig.5 Output of RFT and PC-RFT

图6 RFT与PC-RFT所得目标速度切片处的距离维输出Fig.6 Range dimension output at target’s velocity slice from RFT and PC-RFT
与前面所述的RFT与PC-RFT方法相比,ARFT可以有效地抑制杂波,并在同一距离单元内同时积累运动目标的信号,如图7(a)所示。图7(b)中APCRFT的结果与图7(a)类似,杂波被有效地抑制,运动目标的能量得到有效地聚焦。另外需注意的是,以上所有方法所用的速度搜索空间[-vmax,vmax]超出了最大不模糊速度(已知本实验最大不模糊速度为150 m/s),因此速度维每相隔150 m/s就会在距离-速度网格处产生能量积累,即盲速旁瓣(Blind-Speed Sidelobes,BSSL)[10]。不过凭借其他盲速搜索到的积累数据是不准确的,无法完全相参,因此无法达到媲美目标主瓣的聚焦效果,便成为了旁瓣。而由于跨距离走动,图中盲速旁瓣在其他距离单元处出现扩散。虽然其他距离单元并不是目标所在距离单元,但是以该距离单元和盲速构成的距离-速度网格搜索到的积累数据依然可能与目标真正对应的积累数据发生重叠。即使通过这样错误的网格,搜索得到的积累数据仍然与盲速的多普勒导向矢量部分相参,因此同样无法达到目标主瓣那样的聚焦效果。
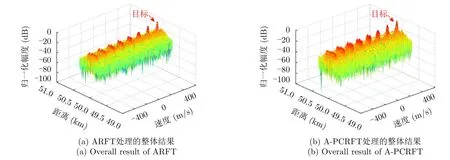
图7 ARFT和A-PCRFT处理结果Fig.7 Output of ARFT and A-PCRFT
与图6相似,图8所示目标速度切片中A-PCRFT方法由于补偿了脉内多普勒,目标主瓣未发生偏移,而ARFT方法无法补偿脉内多普勒,产生了主瓣偏移。由此更加说明A-PCRFT方法结合了ARFT方法与PC-RFT方法的优点,既可以实现杂波抑制,又可以补偿高速目标能量聚焦时不可忽略的脉内多普勒。
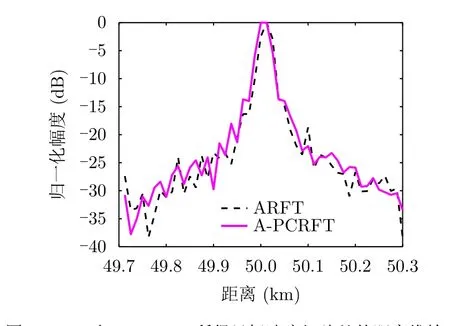
图8 ARFT与A-PCRFT所得目标速度切片处的距离维输出Fig.8 Range dimension output at target’s velocity slice from ARFT and A-PCRFT
进一步比较ARFT与A-PCRFT的性能差异。图9为ARFT与A-PCRFT处理结果中目标所在距离单元处的速度维输出对比。由此可见,A-PCRFT方法相比ARFT方法对目标的盲速旁瓣与背景都有进一步的抑制作用。
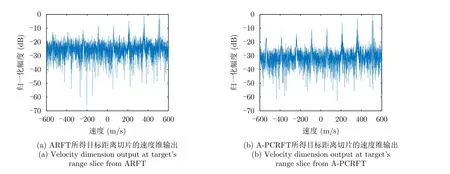
图9 ARFT与A-PCRFT速度维输出结果对比Fig.9 Comparison of velocity dimension output result between ARFT and A-PCRFT
图10在图7的基础上得到ARFT与A-PCRFT处理结果的平面颜色图,用于进一步说明目标与背景的对比关系,可见A-PCRFT方法的杂波抑制能力更强。此外,本实验还设置了目标与周围距离-速度网格的平均信杂噪比(Average SCNR,ASCNR)作为量化指标,计算规则为目标的功率与距离上[rC-ra/2,rC+ra/2]范围内,速度上与vT相差±75 m/s范围内的距离-速度网格的功率平均值进行比较

图10 ARFT与A-PCRFT输出平面图对比Fig.10 Comparison between the plane figures of ARFT and A-PCRFT
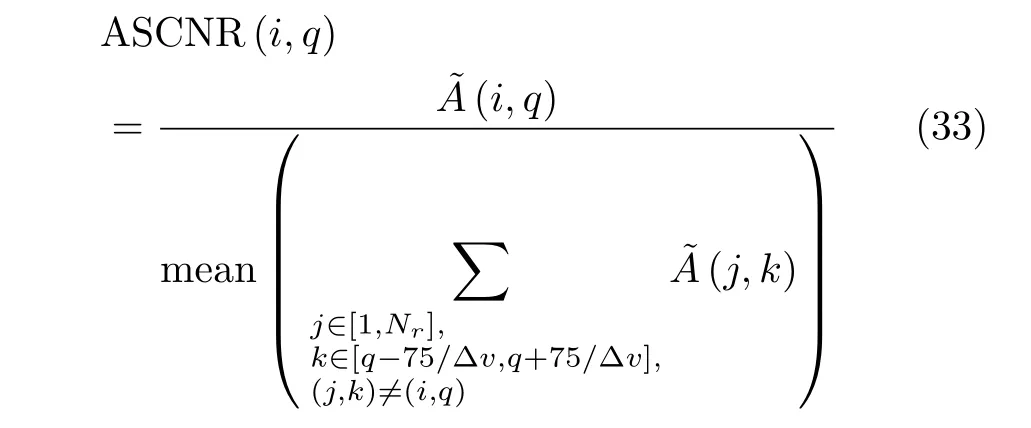
无论是目标径向速度还是积累时间的增加,目标跨距离单元走动效应都会变得越来越严重。假设目标的速度vT不变,然后分析ARFT与A-PCRFT的ASCNR与相参积累时间的关系,如图11所示。结果表明,ARFT与A-PCRFT平均信杂噪比将随着积累时间的增加而增加,同时A-PCRFT方法输出的平均信杂噪比一直优于ARFT方法输出的平均信杂噪比。
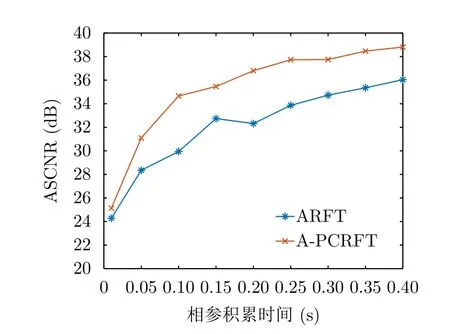
图11 ARFT与A-PCRFT输出的平均信杂噪比与相参积累时间的关系Fig.11 Relationship between coherent accumulation time and ASCNRs of ARFT and A-PCRFT methods
另外,利用本节仿真实验条件,在Matlab R2021b和Intel Core i7-9750H的软硬件平台上,ARFT与A-PCRFT方法对目标所在距离-速度网格(i,q)一次聚焦的计算复杂度关于相参积累脉冲数Np变化的曲线如图12所示。图中横坐标为相参积累时间,纵坐标为对目标所在距离-速度网格一次聚焦的具体耗时。根据图12可直观地看出级联形式和时-距联合的运算效率差别,也证实了时-距联合的计算复杂度随着相参积累时间的增加越来越高于级联形式。
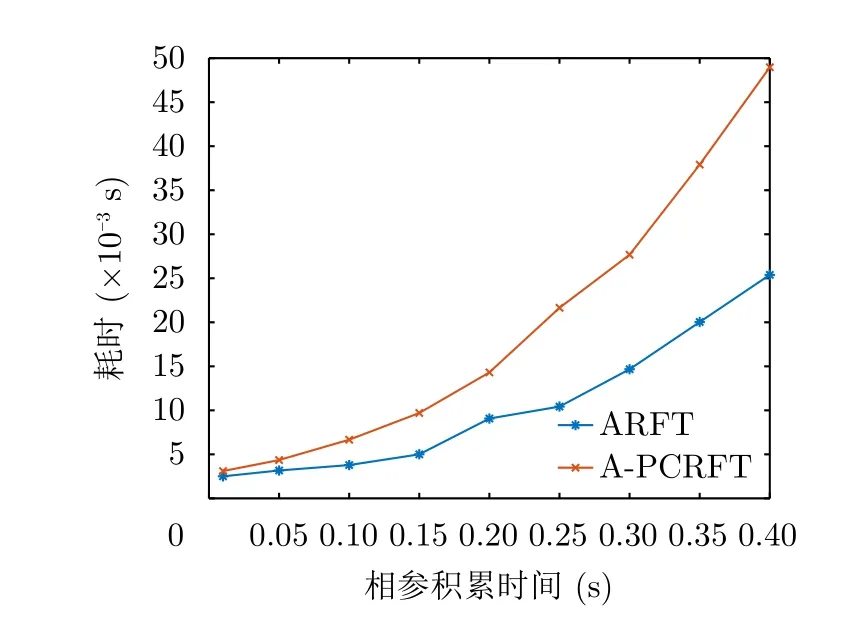
图12 ARFT与A-PCRFT的运算时间与相参积累时间的关系Fig.12 Relationship between coherent accumulation time and operation time of ARFT and A-PCRFT
6 结语
本文按照多维联合检测前聚焦中时(慢时间)-距(快时间)联合的思想,提出了一种将脉冲压缩、Radon-Fourier变换与自适应杂波抑制相结合的时距联合检测前聚焦方法(A-PCRFT)。该方法结合能够抑制杂波的ARFT方法与能够补偿脉内多普勒的脉冲压缩方法,在脉冲压缩前就通过联合脉冲压缩和RFT从协方差矩阵未知的高斯杂波背景中对未知跨距离走动目标的能量聚焦。由于在聚焦过程中利用了脉内和脉间的信息,该方法相比于ARFT方法提高了信杂噪比,但运算量方面联合处理明显要高于级联处理。此外,非均匀杂波背景也是影响APCRFT处理的一大因素,关于这一点我们认为子孔径的方法同样适用于A-PCRFT方法。因此,下一步计划就是将子孔径方法以及其他降维算法用于A-PCRFT方法,进一步提高计算效率,降低对辅助数据量的要求。
