基于STFT谱图滑窗相消的微动杂波去除方法
2022-11-01万显荣谢德强易建新胡仕波
万显荣 谢德强 易建新 胡仕波 童 云
(武汉大学电子信息学院 武汉 430072)
1 引言
微多普勒效应(简称微动效应)是由目标或其部件的微动(如转动、振动、进动等)引起的频率调制现象[1,2]。对雷达系统来说,微动效应是一把“双刃剑”,一方面它能够反映目标的几何结构和运动状态,为目标参数估计、分类识别等应用提供宝贵的特征信息[3,4]。另一方面它也是雷达系统中的一种特殊杂波源,会抬高噪声基底,掩盖弱目标,造成虚警和漏检[5,6]。本文针对微动杂波去除问题展开研究。
微动杂波是一种时变非平稳杂波,往往具有较大的多普勒拓展,常规动目标指示(Moving Target Indicator,MTI)或时域杂波对消类方法很难取得令人满意的效果[7,8],而空域杂波抑制方法则要求杂波和目标在空域上是可分的,否则目标和杂波会被同时抑制[9]。目前,微动杂波抑制方法主要分为参数化和非参数化。参数化方法要求对微动杂波进行精细建模,若模型无法反映杂波真实特性,将会因为模型失配导致算法性能下降甚至失效。文献[10,11]均按扇叶回波的积分模型生成正交匹配追踪(Orthogonal Matching Pursuit,OMP)的字典矩阵,实现微动参数估计、微动杂波稀疏重构及微动杂波去除等功能。显然模型中未知参数的个数决定了字典矩阵的维数及算法的计算量。与上述方法不同,文献[12-14]将微动回波建模为正弦调频(Sinusoidal Frequency-Modulated,SFM)信号,并分别利用逆拉东变换(Inverse Radon Transform,IRT)、正弦调频Fourier-Bessel变换(Sinusoidal Frequency Modulation Fourier-Bessel Transform,SFMFBT)及参数最优匹配等方法解决后续的微动参数估计与抑制问题。相比于上述各种参数化方法,非参数化方法对信号模型的依赖程度大大减弱,因此往往具有操作简便、适用范围广等优点。目前,常用的非参数化方法有经验模态分解(Empirical Mode Decomposition,EMD)[15]、局部均值分解(Local Mean Decomposition,LMD)[16]、独立成分分析(Independent Component Analysis,ICA)[17]等通用的信号分解类算法。此外,由于微动杂波和目标回波在时频域中的形态表现具有明显差异,基于时频变换的信号分离方法也得到了广泛研究[18,19]。文献[20]提出了一种基于L-statistics算法的微动杂波与目标回波分离方法。该方法对信号的短时傅里叶变换(Short-Time Fourier Transform,STFT)谱图沿时间维进行排序,然后舍弃适当比例的强信号成分,达到去除微动杂波的目的。该方法操作简单且具有较强鲁棒性,但它在去除杂波的同时也对目标能量造成较大损失。文献[21]利用遗传算法对上述L-statistics算法造成的目标损失进行补偿,但补偿算法计算量较大。
考虑到L-statistics的上述局限,本文提出了一种基于STFT谱图滑窗相消的微动杂波去除方法。首先介绍了STFT变换的相关性质并说明了微动杂波和目标回波在STFT谱图中的形态表现。然后详细描述了所提方法的实现思路和具体步骤。最后用仿真和实测数据验证了所提方法的有效性,并与Lstatistics算法进行了性能对比。本文所提方法对相干积累时间内,非机动目标探测场景中的非平稳杂波(以风电机组微动杂波为典型代表)有较好的去除效果。
2 短时傅里叶变换
离散形式的STFT可以表示为

其中,w(n)表 示窗函数,其有效窗长为Nw,R表示相邻窗之间的时间步进,m∈[0,M)表示时间单元,M=(N -Nw)/R+1」表 示时间维数,·」表示向下取整操作,k∈[0,N -1]表示频率单元。将式(1)沿时间维叠加,可得


式(1)和式(2)需要注意如下问题:一是式(1)中傅里叶变换的点数需与原始数据长度保持一致,以保证时频变换的频率分辨率与原始数据傅里叶变换的频率分辨率相同,省去后续频谱重构过程中的插值操作;二是COLA条件满足与否既与窗函数类型有关,也与步进值R有关,不失一般地,本文后续的仿真和实测数据处理过程均采用Hamming窗,且步进值设置为R=Nw/2。图1为使用Hamming窗时的COLA验证,圈线表示(n),点线表示M个移位窗函数w(n-mR)。从图1可以看出COLA条件仅在中间部分满足,且此时C=1.08。窗函数两端并不满足COLA条件,由于实际应用中往往满足N ≫Nw,所以通常可忽略该问题。此外,该问题也可通过对原始数据首尾补零加以解决。

图1 Hamming窗R =Nw/2时的COLA验证Fig.1 Validation of the COLA compliant for Hamming window when R=Nw/2
若原始信号中共包含Q个信号分量,则STFT谱图可以表示为[23]

其中,第2个等式中|Sq(m,k)|2表示各个信号成分的自相关项,Sq(m,k)(m,k)表示不同信号成分之间的互相关项。STFT是一种线性变换,它会在各个信号成分的瞬时频率(Instantaneous Frequency,IF)处形成能量集聚,最终STFT谱图中会形成反映各个信号成分瞬时频率的强能量条带[24]。式(3)中互相关项仅出现在各个信号分量瞬时频率的交叉处[23]。
3 目标回波和微动杂波时频特征分析
不失一般地,设发射信号为s(t)=exp(j2πfct)。其中,fc为载波频率。接收信号中包含P个目标回波及I个微动杂波,且设目标在相干积累时间内保持匀速运动。则t时刻目标散射点和微动杂波散射点与雷达的距离可以表示为

其中,Rp,0和Ri,0分别表示第p个目标散射点和第i个微动杂波散射点与雷达的初始距离。vp表示第p个目标散射点的速度。vi,li,ωi,θi分别表示第i个微动杂波散射点的平动速度、旋转半径、旋转速度以及初始相位。则下变频处理后的雷达回波可表示为

第i个微动杂波的瞬时频率可表示为
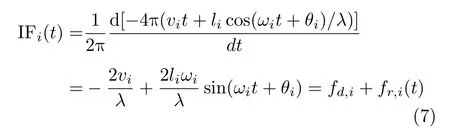
从式(6)和式(7)可以看出,目标回波的瞬时频率即为其多普勒频率,在相干积累时间内保持恒定。微动杂波的瞬时频率随时间呈正弦函数变化。因此,目标回波在STFT谱图中将表现为特定频率单元上的直线型能量条带(后文中均将“能量条带”简称为flash),而微动杂波在STFT谱图中则表现为横跨多个频率单元的正弦形式的flash。
进一步地,对于长度为L、转速为ω的旋转叶片,其微动杂波可由叶片上所有散射点回波叠加而成,即回波表达式为

其中,θ0为初始相位。由文献[25]可知,此时叶片回波在STFT谱图中包含多种不同形态的能量条带,具体包括:垂直于时间轴的矩形flash、正弦型flash和零频直线型flash。特别地,当叶片数目为偶数时,零频直线型flash将不再出现在STFT谱图中。
综上所述,目标回波和微动杂波在STFT谱图中的表现形态存在较大差异。目标回波表现为特定频率单元上的直线型flash,而微动杂波则会在一定频率范围内的多个频率单元上呈现复杂的分布形态。
4 基于STFT谱图滑窗相消的微动杂波去除
通常可认为,当相干积累时间较短时,目标做匀速运动且其回波幅度保持相对平稳,因此目标回波在STFT谱图中表现为与时间轴平行的直线型flash。而微动杂波具有时变非平稳特性,它在STFT谱图中表现为横跨多个频率单元的具备复杂形态的flash。利用目标回波和微动杂波在STFT谱图中的不同表现形态,将两者分离开来,进而实现微动杂波去除是所提方法的基本思路。
利用图2对所提算法的基本原理进行直观说明。图2中微动杂波中表现为正弦型flash,目标回波表现为直线型flash。利用两个等长的窗(分别称为参考窗和滑动窗)从原始STFT谱图中截取得到两个时频子图,分别称为参考窗谱图和滑动窗谱图。将两个谱图对应位置上的元素进行相减。由于两个谱图中目标flash位于相同频率单元上,相减后目标flash被极大削弱。而两个谱图中微动flash相互错开,相减操作对其影响较小。最终,根据相减前、后谱图中各位置的能量变化情况,即可确定出目标flash和微动flash在STFT谱图中的位置,从而实现两者在STFT谱图上的分离。不过,从图2可以看出,在参考窗谱图和滑动窗谱图对应元素相减的过程中,若两个谱图在同一位置上都存在微动flash,即图2红色圆圈所示的重叠交叉位置,则相减后,该位置上的能量也可能被极大削弱,进而会将其判定为目标flash,降低了两者分离的效果。
为克服上述问题,将图2中滑窗方法进一步拓展为前、后向同时滑窗的形式,通过综合多次滑窗相消结果,提高微动flash和目标flash的分离效果,算法包含的步骤如下:

图2 所提算法基本原理示意图Fig.2 Diagram of the basic principle of the proposed method
步骤1 设积累时间内的数据为x(n)(0≤n ≤N -1),对其进行满足COLA约束的STFT变换,得到S=[s0,s1,...,sM-1] 。其中,sm=[s0,s1,...,sN-1]T表示第m个窗内数据的傅里叶变换结果。令Y(k,m)=|S(k,m)|2(0≤m <M,0≤k <N)表 示STFT谱图,即Y=[y0,y1,...,yM]。以STFT谱图时间维中点为分界线,获取式(9)所示前、后参考窗STFT谱图

从式(9)可以看出,前、后参考窗STFT谱图的维数均为N×(M/2)。
步骤2 对原始STFT谱图按图3所示方式进行滑窗。设共进行Q次滑窗,窗长为M/2,则相邻窗之间的步进为 ΔM=/(2(Q+1))」。第q(1≤q ≤Q)个滑窗STFT谱图可以表示为Yq=[yqΔM,yqΔM+1,...,yqΔM+M/2-1]。

图3 滑窗示意图Fig.3 Diagram of the sliding window
步骤3 将前、后参考窗STFT谱图分别与各个滑窗STFT谱图进行对应元素相减,并计算相减结果与原始前、后参考窗STFT谱图对应元素的比值,即

步骤4 设置门限ΔP用于表征向前、后参考窗谱图中每个位置上的能量变化情况,并定义如下变量

其中,IF,q(k,m)=1,IB,q(k,m)=1分别表示前、后参考窗STFT谱图中 (k,m)位置上存在微动flash。综合Q次滑窗的结果,定义如下参数
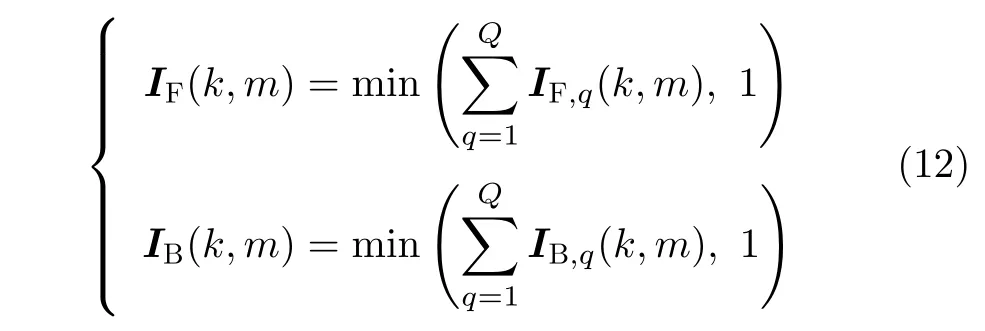
其中,min(x,1) 表示取小运算符,即:若x<1,min(x,1)=x,否则 m in(x,1)=1。
最终地,IF(k,m)=1,IB(k,m)=1分别表示前、后参考窗STFT谱图中 (k,m)位置上存在微动flash。
步骤5 综合前、后参考窗STFT谱图微动flash的位置信息,可从原始STFT数据中提取出微动杂波的STFT数据,具体操作如下
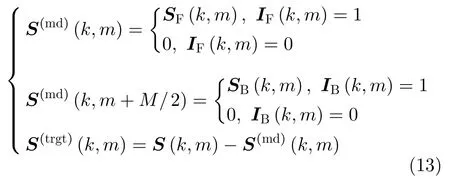
其中,S(md)为 分离后微动杂波的STFT数据,S(trgt)为目标回波的STFT数据。
步骤6 将S(md)和S(trgt)分别沿时间维叠加,即可得到微动杂波和目标回波的频谱,具体地

其中,C表示窗函数的COLA常数,当STFT变换过程采用Hamming窗,且相邻窗函数的重叠长度为窗长的一半时,C=1.08。由式(14)可进一步利用傅里叶逆变换得到微动杂波和目标回波的时域数据,即x(md)=ifft(X(md)),x(trgt)=ifft(X(trgt))。其中,ifft(·)为傅里叶逆变换函数。
综上所述,所提算法的流程图如图4所示,并将该算法称为STFT谱滑窗相消(STFT Spectrum Sliding Cancelation,STFT-SSC)。

图4 STFT谱滑窗相消算法流程图Fig.4 Diagram of the STFT-SSC method
5 仿真与实验验证
5.1 多散射点微动杂波去除仿真验证
仿真信号表达如式(5)所示,其中P=I=3,表示回波信号中包含3个目标散射点和3个微动杂波散射点的回波分量。系统采样率设置为2000 Hz,积累时间为2 s,信号波长λ=0.46 m。3个目标的信噪比分别为[-5,20,5] dB,多普勒频率分别为fd,p=[800,-300,300] Hz ,p∈[1,3]。3个微动杂波的杂噪比分别为[30,25,20] dB,其余各参数分别为fd,i= [-140,-100,100] Hz,li=[13.61,27.21,5.88] m,ωi= [4.25π,1.40π,7.40π] rad,θi=[0.7π,0,1.3π] rad。仿真生成的原始信号及其STFT谱图如图5所示。可见,微动杂波频率范围为-936~699 Hz,3个微动杂波分量在STFT谱图中呈现互相交叉重叠的复杂分布形态。2个目标(-300 Hz和300 Hz)位于微动杂波带宽内,它们与微动杂波在STFT谱图中互相交叉。多普勒频率为800 Hz的弱目标位于微动杂波带宽外,它在STFT谱图中与其他信号分量不存在交叉。

图5 多散射点微动杂波仿真信号的频谱和STFT谱图Fig.5 Spectrum and STFT spectrogram of the simulated signal with multiple scattering points micro-motion clutter
利用本文所提STFT-SSC算法和L-statistics算法分别对仿真信号进行处理,其中STFT-SSC算法滑窗个数设为6,门限值ΔP设为0.7。L-statistics的数据舍弃比例设置为0.7,即将每个频率单元上的强度排在前70%的位置上的成分均认为是微动杂波。处理结果如图6所示。将STFT-SSC算法在前、后参考窗中分离得到的目标回波和微动杂波的STFT谱图整合到一起,得到图6(a)和图6(b)所示的分离结果,可以看出,两种信号分量整体上得到了较好的分离,但是在目标和微动能量条带交叉位置上可能存在分离效果降低的现象。下面分析在上述交叉位置上STFT-SSC算法的分离性能。当微动杂波的能量远强于目标时,两者交叉位置将被判定为微动杂波,此时交叉位置上的目标会和微动杂波一起被去除,造成目标能量的损失。不过,由于微动杂波对应被去除的能量更多,分离后,目标的信杂比(目标能量/微动杂波能量)仍然会有得益。当目标能量远强于微动杂波时,两者交叉位置将被判定为目标回波,此时交叉位置上的目标回波和微动杂波均会被保留下来,造成微动杂波残余。不过,此时保留下来的微动杂波能量很小,对目标信杂比影响较小。从图6(a)可以看出,频率为800 Hz的目标与微动杂波不存在交叉,因此被完全保留下来。频率为300 Hz的目标与微动杂波存在严重交叉,且其强度较弱,因此交叉处被判定为微动杂波,造成该目标能量的部分损失。频率为-300 Hz的目标虽然与微动杂波存在严重交叉,但其强度与微动杂波相当,因此交叉处并未被全部判定为微动杂波,其能量损失较少,但其微动杂波残余较多。上述分析结果在图6(c)的目标频谱分离结果中得到了较好的验证。从图6(c)可以看出-300 Hz,300 Hz以及800 Hz的目标的能量损失分别为0.58 dB,4.52 dB,0.31 dB。
图6(d)和图6(e)为L-statistics算法分离后的目标回波和微动杂波的STFT谱图。由图6(d)可以看出,无论目标回波与微动杂波是否存在交叉,L-statistics均会损失较大的目标能量。从图6(f)可以看出-300 Hz,300 Hz以及800 Hz的目标的能量损失分别为12.04 dB,12.43 dB,12.95 dB。同时比较图6(c)和图6(f)可以看出L-statistics处理后的噪底相对较低。上述现象的解释如下:在目标所在频率单元上,目标沿时间维是稠密分布的,因此其中有较大比例单元上的目标能量强于L-statistics阈值,这部分目标单元将被当成微动杂波去除,造成目标能量损失。在其他频率单元上,微动杂波沿时间维是稀疏分布的,去除该频率单元上的微动杂波后,还有较大比例的噪声单元会被当成微动杂波去除。

图6 STFT-SSC和L-statistics算法多散射点微动杂波处理结果对比Fig.6 Comparison of the processing results between the STFT-SSC and L-statistics for multi-scattering points micro-motion clutter
5.2 叶片旋转微动杂波去除仿真
仿真回波中包含3个目标分量,其参数设置与5.1节中目标参数一致。另外仿真了两组叶片引入的微动杂波,每个叶片回波信号模型如式(8)所示。具体地,第1组叶片数为3,相邻叶片间隔60°,叶片长度为10 m,转速为150 r/min,且其附带的平动多普勒频率为-220 Hz。第2组叶片数为2,相邻叶片间隔180°,叶片长度为8 m,转速为171 r/min,且其附带的平动多普勒频率为100 Hz。仿真信号波长为0.45 m,采样率为2000 Hz,积累时间为2 s。仿真信号的频谱和STFT谱图如图7所示。
图7(a)和图7(b)与5.1节类似,有一个弱目标位于微动杂波带外,一强一弱两个目标位于微动杂波带内。3叶片微动杂波在STFT谱图中表现为沿时间轴周期性分布的强竖直能量条带、弱直线能量条带以及弱正弦能量条带。2叶片微动杂波的STFT谱图以其平动多普勒频率为对称轴,呈现频率轴上的对称性,且其不包含延时间轴的直线能量条带。两组微动杂波及目标回波在STFT谱图中呈现复杂的互相交叉重叠的情况。
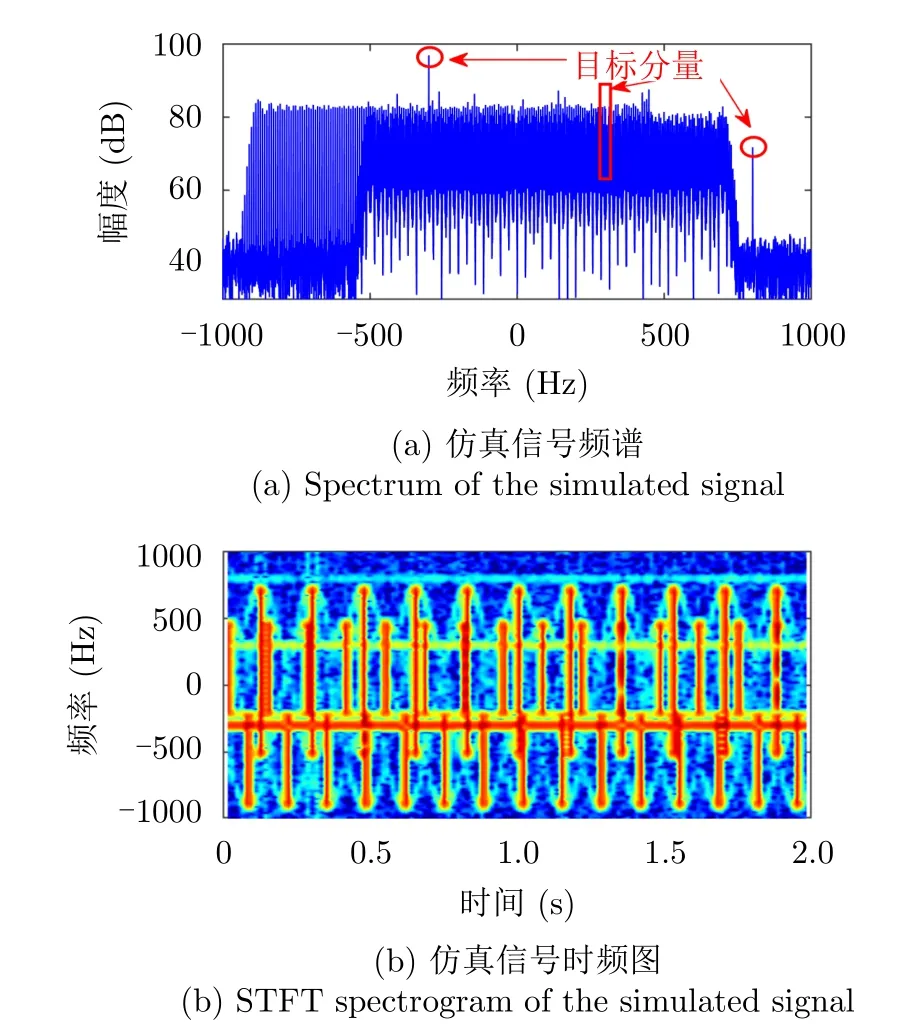
图7 旋转叶片微动杂波仿真信号的频谱和STFT谱图Fig.7 Spectrum and STFT spectrogram of the rotating blade micro-motion clutter simulation signal
利用STFT-SSC算法和L-statistics算法对上述仿真数据进行处理。两种算法所用参数与5.1节一致。对比图8中两种算法的处理结果可以得出与5.1节一致的结论,即STFT-SSC算法比L-statistics算法具有更好的目标回波和微动杂波的分离效果。具体地,从图8(c)可以看出STFT-SSC算法-300 Hz,300 Hz和800 Hz的目标能量损失分别为0.65 dB,3.93 dB,0.59 dB。而从图8(f)得到的Lstatistics算法中上述3个目标的能量损失分别为13.49 dB,11.85 dB和12.86 dB。值得注意的是,从图8(c)和图8(f)中-220 Hz附近出现类似目标的谱峰,这是由3叶片微动杂波在STFT谱图中的弱直线能量条带引入的。偶数叶片的微动杂波中不会出现上述峰值。

图8 STFT-SSC和L-statistics算法旋转叶片微动杂波处理结果对比Fig.8 Comparison of the processing results between the STFT-SSC and L-statistics for rotating blade micro-motion clutter
5.3 实测风电机组微动杂波去除
武汉大学研究者利用自主研制的基于数字电视信号的外辐射源雷达系统在河南洛阳某地开展了风电机组微动探测实验。雷达探测场景图如图9所示,相关实验配置见文献[26]的2.4节(风电机组扇叶微多普勒探测结果)的内容。其中探测目标为大疆无人机(精灵Phantom 4 Pro,轴距350 mm),探测场景中存在多个风电机组,引入了严重的微动杂波。实验过程中,无人机以约 15 m/s 的速度远离雷达飞行。

图9 实验场景图Fig.9 Experimental scene
图10为原始信号频谱和STFT谱图,可以看出在无人机的多普勒频率约为-60 Hz。将图10(b)与图7(b)进行对比,可以发现图7(b)中竖直能量条带在图10(b)呈现出弯曲倾斜的状态,这是由于风电机组叶片长度较大(约56.8 m),而雷达和风车距离较近(约610 m),因此叶片处于近场探测区[27]。此外,图10(b)零频处的能量条带强度较大,主要包含两个信号成分,一个是由叶片的微动效应引入的微动杂波,另一个是机组塔架引入的固定杂波。利用STFT-SSC算法和L-statistics算法对上述实测数据进行处理。两种算法所用参数与5.1节一致。从图11的处理结果可以看出两种算法均能有效抑制微动杂波。但是相较而言,STFT-SSC算法对目标回波和微动杂波的分离效果更好,目标能量损失较少。具体地,从图11(c),图11(f)可以看出两种算法处理后目标的能量损失分别为3.80 dB和19.00 dB。选取目标谱峰左右两边的第40~100个多普单元作为杂波能量统计的参考窗,可得STFT-SSC算法抑制后信杂比由12.38 dB提高到30.44 dB,而L-statistics算法抑制后信杂比只提高到22.03 dB,由此可见STFT-SSC算法具有更好的信杂比改善效果。此外,需要注意的是,对于两种算法来说,均会在一定程度上保留图10(b)所示的零频能量条带,因此图11(c),图11(f)在零频附近均存在较多杂波残余,对其可后续通过常规动目标指示(Moving Target Indicator,MTI)或时域杂波对消类方法进一步去除[7,8]。

图10 原始信号频谱和STFT谱图Fig.10 Spectrum and STFT spectrogram of the original signal
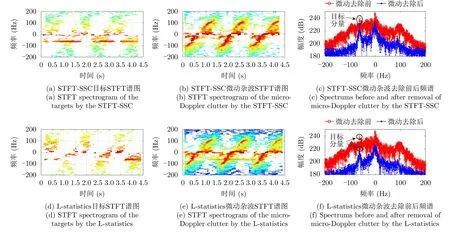
图11 STFT-SSC和L-statistics实测处理结果对比Fig.11 Comparison of the processing results of field experimental data between the STFT-SSC and L-statistics
6 结语
本文利用微动杂波和目标回波在STFT谱图中的形态差异,提出了一种基于STFT谱图滑窗相消的微动杂波去除方法。在相干处理时间内,由于微动杂波在STFT谱图中呈现覆盖多个频率单元的复杂形态,而匀速或速度慢变的目标回波仅在某些频率单元上呈简单的直线分布,因此将时间滑窗后的STFT谱图与原始STFT谱图相减,即可根据相减前后的强度变化程度将两者分离。文中分别根据微动杂波散射点的SFM信号模型以及叶片微动回波的积分模型对STFT-SSC算法进行了仿真验证,证明了STFT-SSC算法的有效性。此外,实测风电机组的微动杂波数据处理结果进一步表明,相比较Lstatistics算法,STFT-SSC算法具有更好的目标回波和微动杂波分离效果,能够较好地减少目标能量损失。后续研究将结合插值或信号重构类方法补偿或恢复杂波去除过程中造成的目标能量损失。
