面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法
2022-11-01时晨光王奕杰代向荣周建江
时晨光 王奕杰 代向荣 周建江
(南京航空航天大学雷达成像与微波光子技术教育部重点实验室 南京 210016)
1 引言
当今空战正逐步由信息化向智能化过渡,并呈现出体系博弈对抗的发展趋势。电磁频谱环境的复杂性、时变性与难以预测性、非合作目标的多样性、运动的复杂性与作战使用的灵活性,给单平台雷达探测系统提出了严峻的挑战。通过多雷达协同组网能够显著提高目标探测跟踪能力、电磁对抗能力与战场生存能力,已成为国内外学者和研究人员的共识。机载组网雷达是基于“网络赋能”思想,将多部不同体制、不同频段、不同工作模式的机载雷达分散部署,借助机间通信链路,将多部机载雷达获得的目标信息进行融合处理,由融合中心统一指挥而构成的有机整体[1,2],是分布式作战、马赛克战等先进作战理论的重要抓手。机载组网雷达在空间上可以是广域分布或近距离短基线分布,能够利用空间分集、信号分集、极化分集等优势有效对抗复杂电磁频谱环境,提高系统的整体作战性能。
组网雷达作为一种新体制雷达,在目标检测、跟踪、识别等诸多场景中均具有潜在优势,受到了国内外众多学者的关注。射频资源管理和发射波形选择对于组网雷达而言至关重要,通过优化辐射采样间隔、驻留时间、辐射功率、信号脉冲宽度和信号带宽等射频参数,能够有效提升雷达系统性能。2018年,Cheng等人[3]在目标协同跟踪场景,提出了基于共址多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达的自适应资源管理算法,通过联合优化系统的子阵数、照射目标集和发射波形,同时降低目标跟踪误差和系统辐射资源消耗。2019年,张浩为等人[4]在目标跟踪场景下,将自适应匀速模型与平方根容积卡尔曼滤波相结合,通过调整过程状态噪声与滤波器输出的状态协方差矩阵相似,实现了发射信号波形的自适应调整,从而进一步提升了目标跟踪精度。2020年,文献[5]提出了一种非理想检测环境下多基雷达系统多目标跟踪功率分配算法,推导了非理想检测环境下目标运动状态估计的后验克拉默-拉奥下界(Posterior Cramér-Rao Lower Bound,PCRLB)解析表达式,并采用了基于Zoutendijk可行方向法的两步分解算法对该优化问题进行求解。仿真结果表明,与现有算法相比,所提算法能够有效提升非理想环境下多基雷达的目标跟踪能力和资源利用率。同年,文献[6]研究了共址MIMO雷达时空资源分配和波形选择优化联合问题,通过同时最小化系统资源消耗和目标跟踪误差,在保证有效目标检测的约束条件下,对雷达采样周期、子阵数、照射目标、辐射能量和发射波形等参数进行自适应优化选择,从而提升系统性能。2021年,文献[7]提出了共址MIMO雷达稳健功率分配算法,采用所有目标效用函数的加权和作为优化目标,解决了传统资源管理方法中雷达总辐射功率消耗无法满足给定多目标跟踪性能要求的问题。
机载组网雷达系统工作性能不仅受各雷达辐射参数的影响,还高度依赖各机载雷达的空间位置。在实际作战中,采用合理的航迹规划策略,能够有效提升机载系统的作战效能。文献[8]针对一个共用固定雷达发射机和多个机动雷达接收机构成的多基地雷达系统,在单目标跟踪场景下,提出了一种雷达发射波形和接收机路径联合优化算法,通过最小化目标跟踪误差,对雷达发射波形和接收机飞行路径进行联合优化设计,从而提升了多基地雷达系统的目标跟踪性能。2019年,孟令同[9]提出了机载相控阵雷达飞行路径和功率联合管控算法,以最差情况下的目标跟踪克拉默-拉奥下界(Cramér-Rao Lower Bound,CRLB)为优化目标,以载机机动限制和系统辐射功率限制为约束条件,对平台飞行路径和雷达辐射功率进行联合动态优化。仿真结果表明,相比于均匀功率分配下的飞行路径优化策略,所提算法获得了更优的目标跟踪性能。2020年,Dasdemir等人[10]以总飞行距离和雷达检测威胁最为优化目标,采用一般偏好的多目标进化算法进行求解,并通过决策者偏好确定最终最优解,解决了雷达检测威胁下的无人机路径规划问题。同年,张哲等人[11]提出了一种基于改进A-star算法的隐身无人机突防航迹规划算法,在传统A-star算法的基础上,将雷达探测概率和无人机RCS与启发函数相结合,考虑了规划航迹下的无人机隐身性能。仿真结果表明,改进A-star算法能够快速生成更优的隐身突防航迹,具有一定的应用价值和现实意义。2021年,文献[12]提出了多目标跟踪场景下的机载雷达飞行路径和辐射资源联合优化设计算法,以目标运动状态估计的PCRLB为优化目标,在满足雷达资源约束条件下,联合优化设计飞行路径和辐射资源,从而有效提升了机载雷达目标跟踪性能。魏永超等人[13]提出了基于改进细菌觅食优化算法的无人机路径规划算法,以路径最短约束、飞行高度约束和转弯角约束的加权和为目标,采用改进细菌觅食优化算法迭代获得最优路径。所提算法将固定步长改为自适应步长,将固定迁徙概率改为自适应迁徙概率,解决了现有的无人机航迹规划方法收敛速度慢、效率低等问题。同年,廖文旭[14]考虑了多威胁环境对无人机航迹规划的影响,提出了基于Dijkstra的改进航迹规划算法,以已知威胁和燃油代价作为多目标代价约束,解决了无人机单机侦察任务的静态规划问题。
然而,近年来,大量先进无源探测系统和无源探测模式被广泛应用于现代战争中。无源探测系统自身不辐射电磁波,而是通过截获有源电子设备辐射的电磁波来获取对方武器平台的位置信息,具有探测距离远、隐蔽性好等特点,对机载组网雷达的战场生存和突防造成了极大威胁。雷达射频隐身技术作为一种不可或缺的有源隐身技术,是对抗敌方无源探测系统、保障己方战斗机安全并获取战斗先机的重要手段,其主要原理是在保证系统性能和作战任务的情况下,最大限度地降低雷达射频辐射特征,从而减小被敌方探测系统截获的概率[15,16]。2018年,Yan等人[17]在多目标定位场景下,提出了基于机会约束的共址MIMO雷达稳健功率分配算法,以最小化系统总发射功率作为优化目标,对各波束发射功率进行自适应优化分配,从而解决了目标雷达散射截面(Radar Cross Section,RCS)不确定场景下的功率分配问题。同年,文献[18]针对由一部雷达发射机和多部雷达接收机构成的多基地组网雷达,研究了基于射频隐身的多基地组网雷达辐射资源控制问题,以最小化多基地组网雷达被截获概率为优化目标,在满足目标跟踪误差和系统资源约束条件下,对雷达发射机采样间隔、发射功率和驻留时间进行优化,从而提升了系统射频隐身能力。2019年,Dai等人[19]在多目标跟踪场景下,提出了相控阵雷达(Phased Array Radar,PAR)最优资源分配算法,在满足给定目标跟踪精度的条件下,最小化PAR的总资源消耗。仿真结果表明,该算法能够有效降低PAR的驻留时间。同年,赖作镁等人[20]建立了多拍连续引导信息与累积被截获概率和被探测概率之间的函数关系,提出了一种基于马尔可夫决策过程的多传感器协同辐射控制算法,实现了不同作战任务性能约束下的机载雷达射频隐身性能优化。2020年,Ghoreishian等人[21]研究了多基地MIMO雷达功率分配问题,以最小化雷达发射信号的被截获概率为优化目标,分别建立了正交频率分集和相位编码两种发射波形情况下基于射频隐身的功率分配模型,并用凸优化算法求解上述模型,从而降低了多基地MIMO雷达的被截获概率。2021年,文献[22]研究了多目标跟踪场景下的雷达射频隐身问题,建立了组网雷达射频辐射资源优化分配模型,对雷达驻留时间、辐射功率和节点分配方式等参数进行联合优化设计,降低了组网雷达的辐射资源消耗,从而提升其射频隐身性能。
综上所述,上述研究成果为提升机载组网雷达的综合作战效能奠定了坚实基础。然而,已有研究并未考虑目标跟踪场景下将机载组网雷达辐射参数与平台航迹规划进行联合优化设计,这对于提升我方雷达探测系统的射频隐身性能、战场生存能力及其在对抗敌方先进无源探测系统和无源探测模式时的效益,具有重要意义。因此,本文围绕目标跟踪场景下组网雷达辐射资源管理、雷达射频辐射参数控制、飞行器航迹规划等领域,研究了面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化问题。首先,针对机载组网雷达,在单目标跟踪场景下,建立了面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化模型,以最小化机载组网雷达贝叶斯克拉默-拉奥下界(Bayesian Cramér-Rao Lower Bound,BCRLB)为优化目标,以满足机载组网雷达射频资源、载机动力学限制和预先设定的被截获概率阈值为约束条件,通过联合优化各载机飞行速度、朝向角等平台运动参数以及各雷达辐射功率、驻留时间、发射信号高斯脉冲长度、信号带宽等射频辐射参数,提升机载组网雷达的目标跟踪精度。仿真结果验证了所提算法的可行性和有效性。
2 系统模型
2.1 目标运动模型

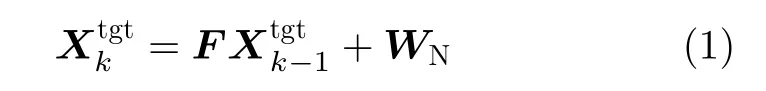
其中,F为目标状态转移矩阵;WN为零均值高斯白噪声,其协方差矩阵Q为

其中,T为雷达采样间隔;为过程噪声强度。
本文采用交互式多模型扩展卡尔曼滤波(Interacting Multiple Model-Extended Kalman Filter,IMM-EKF)算法对单目标进行跟踪。假设目标有3种运动模型,分别为匀速运动模型、正角速度转弯运动模型和负角速度转弯运动模型,其各自对应的目标状态转移矩阵分别表示为
(1) 匀速运动模型

(2) 正角速度转弯运动模型

其中,ω表示转弯因子,且ω>0。
(3) 负角速度转弯运动模型

2.2 载机运动模型
为了保证载机航迹平滑,假设载机在相邻两个时刻间是做匀速直线运动、匀加/减速直线运动或匀加/减速曲线运动,即在k-1 时 刻到k时刻之间,载机的加速度保持不变。如图1所示,定义k时刻第n部载机的朝向角θn,k为 载机飞行朝向与X轴的夹角。已知k-1时 刻第n部载机飞行速度vn,k-1和朝向角θn,k-1以 及k时刻的飞行速度vn,k和朝向角θn,k,则在k-1时 刻到k时刻之间,第n部载机的加速度an,k-1可以表示为

图1 载机运动模型示意图Fig.1 Schematic diagram of the movement model of the carrier aircraft

其中,ax,n,k-1为 第n部载机沿X轴方向的加速度;ay,n,k-1为第n部载机沿Y轴方向的加速度。
在k-1时 刻到k时刻之间,第n部载机沿X轴方向飞行的路程Δxn,k-1和 沿Y轴方向飞行的路程Δyn,k-1可分别表示为

结合k-1时刻第n部载机的位置[xn,k-1,yn,k-1],可得k时刻第n部载机的位置[xn,k,yn,k]为

值得注意的是,在已知k-1时 刻第n部载机飞行速度vn,k-1和朝向角θn,k-1的 情况下,k-1时刻到k时刻之间第n部载机的航迹可由k时刻的飞行速度vn,k和朝向角θn,k确定。因此,优化k-1时刻到k时刻之间的载机航迹就可以等效为优化k时刻载机的飞行速度vn,k和朝向角θn,k。
2.3 量测模型
为简化起见,假设每部机载雷达只能接收自身发射信号的目标回波,且所有机载雷达均从回波信号中提取目标的时延、多普勒频移和方位角信息。于是,k时刻第n部机载雷达对目标的量测方程可以表示为[23]

其中,Pt,n,k为k时刻第n部机载雷达辐射功率;Td,n,k为k时刻第n部机载雷达驻留时间;Gt为机载雷达发射天线增益;Gr为机载雷达接收天线增益;σ为目标RCS;λt为机载雷达发射信号波长;GRP为机载雷达接收机处理增益;Tr为雷达脉冲重复周期;kB为 玻尔兹曼常数;T0为 雷达接收机噪声温度;Br为雷达接收机匹配滤波器带宽;Fr为雷达接收机噪声系数;Rn,k为k时刻目标与第n部机载雷达的距离。
3 机载组网雷达辐射参数与航迹规划联合优化算法
3.1 目标跟踪精度衡量指标
从雷达辐射资源控制角度出发,增加雷达对目标照射的辐射资源,能够提高目标回波信噪比,从而改善目标跟踪性能。从航迹规划角度出发,规划合理的航迹有利于降低雷达与目标之间的距离,并从合适的方位角对目标进行照射,可以进一步提升目标跟踪精度。因此,在建立优化模型之前,需要推导表征目标精度衡量指标的解析表达式。在参数无偏估计的条件下,BCRLB表示均方误差的下界,可以用来衡量机载组网雷达的目标跟踪精度[26-28]。由于量测方程的非线性特征,目标运动状态的BCRLB解析表达式可近似为


3.2 射频隐身性能衡量指标
截获接收机对雷达信号的截获概率可用于衡量雷达的射频隐身性能。在考虑实际战场对抗环境下,假设目标自身搭载截获接收机,并可覆盖机载组网雷达的工作频段。本文讨论的雷达被截获概率是指被跟踪目标上搭载的截获接收机对雷达发射信号的前端截获概率,即[29,30]

其中,e rfc(·)为 互补误差函数;GIP为截获接收机处理增益;T0是 截获接收机噪声温度;BI为截获接收机带宽;FI为截获接收机噪声系数。在给定雷达发射机辐射功率和驻留时间的条件下,k-1时刻第n部机载雷达的被截获概率预测值可以表示为

其中,Rt,k|k-1为k-1时 刻目标与第n部机载雷达之间的距离。
3.3 优化模型建立
本文提出了一种面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法,通过联合优化各载机飞行速度、朝向角等平台运动参数以及各机载雷达辐射功率、驻留时间、发射信号高斯脉冲长度和信号带宽等射频辐射参数,在满足给定系统射频资源、载机机动能力和射频隐身性能约束的条件下,最小化机载组网雷达的目标跟踪误差,可建立如下优化模型
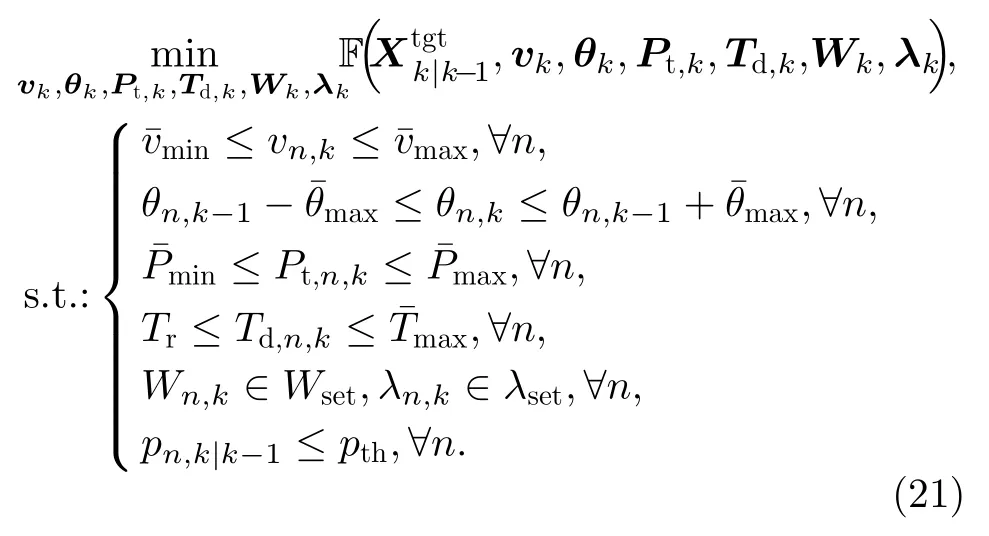
3.4 优化模型求解
优化模型(21)为含有6个变量的非凸、非线性、高维优化问题。虽然传统智能算法,如粒子群算法、遗传算法、模拟退火算法等[31,32]均可用于求解上述优化问题,但优化参数间存在耦合,极其容易陷入局部最优解,不利于算法收敛,且求解时间复杂度过高。为此,本文结合循环最小法和粒子群算法,提出了一种5步分解迭代方法,对机载组网雷达辐射参数与航迹进行自适应联合优化设计,具体求解步骤如下:
步骤1 固定各机载雷达发射波形参数Wk=和λk=,则优化模型(21)可以简化为

步骤2 由于优化模型(22)仍然是非凸、非线性优化问题,目标函数还受到机载组网雷达辐射功率Pt,k、驻留时间Td,k和 各载机飞行参数vk,θk的影响,直接采用粒子群算法进行求解容易得到局部最优解,且收敛速度慢,求解效果不佳。因此,在步骤2中建立机载组网雷达的辐射功率Pt,k、驻留时间Td,k和 各载机的飞行参数vk,θk之间的函数关系,极大地减少了粒子群算法中粒子变量维度,即省略了机载组网雷达辐射功率和驻留时间的维度,加快了粒子群算法的收敛速度。


值得注意的是,当机载雷达的驻留时间取最小值时,其辐射功率可能会超过自身辐射功率的上限。于是,在满足第n部机载雷达辐射功率约束的条件下,其辐射功率可以表示为
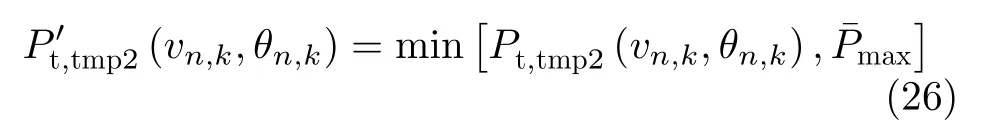
由于第n部机载雷达输出信噪比与驻留时间和辐射功率的乘积成正比,因此,求其最大输出信噪比就等价为求驻留时间和辐射功率乘积的最大值,即

步骤3 采用粒子群算法对优化模型(23)进行求解,在固定机载组网雷达发射信号波形参数Wk,λk的 条件下,得到各载机飞行参数优化结果vk,opt,θk,opt和机载组网雷达辐射参数优化结果Pt,k,opt,Td,k,opt。
在循环迭代过程中,每个粒子都代表一种潜在可行解,根据全局最优粒子和个体最优粒子的位置,不断调整粒子的速度和位置

具体步骤如表1所示。

表1 粒子群算法求解模型(23)Tab.1 Particle swarm algorithm to solve the model (23)
步骤4 固定步骤3获得的各载机飞行参数优化结果vk,opt,θk,opt和机载组网雷达辐射参数优化结果Pt,k,opt,Td,k,opt,则优化模型(21)可以进一步简化为
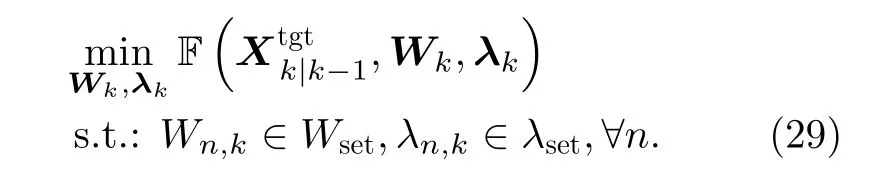
值得注意的是,优化模型(29)同样可以通过粒子群算法进行求解。
步骤5 跳转到步骤3,直到连续两次得到的目标函数之差小于一个固定值ε,即可得到k时刻各载机飞行参数优化结果vk,opt,θk,opt以及机载组网雷达辐射参数优化结果Pt,k,opt,Td,k,opt,Wk,opt,λk,opt,即

4 仿真结果及分析
为了验证面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法的有效性,本节进行如下仿真:假设机载组网雷达系统由N=4部机载雷达组成,各部机载雷达的系统参数均相同,重访时间间隔为T=1 s,跟踪过程持续时间为Mtot=80 s,用于算法结束循环的固定值设置为ε=0.1。其中,机载组网雷达和截获接收机仿真参数设置分别如表2和表3所示。

表2 机载组网雷达参数设置Tab.2 Parameter setting of airborne radar network

表3 截获接收机参数设置Tab.3 Parameter setting of intercept receiver
在仿真场景中,机载组网雷达的初始运动状态如表4所示,被截获概率阈值设定为pth=0.0003。机载组网雷达目标跟踪场景如图2所示。机载组网雷达的飞行速度和朝向角优化结果分别如图3和图4所示。从图中可以看出,各载机能够根据目标运动状态自适应地调节飞行速度和朝向角,且呈现出距离目标越来越近的趋势。图5和图6分别示出了各部机载雷达的辐射功率和驻留时间优化结果。从图中可以看出,各部机载雷达能够根据目标实时运动状态,自适应地选择最小功率策略或最小驻留时间策略对目标进行照射,从而在满足机载组网雷达射频隐身性能要求的条件下,提升系统的目标跟踪精度。图7和图8分别给出了各部机载雷达发射信号高斯脉冲长度和信号带宽优化结果。从图中可以看出,各部机载雷达发射信号高斯脉冲长度和信号带宽均随着目标运动状态的变化而自适应地进行调整,以最大限度地降低目标跟踪误差,从而提升了机载组网雷达的目标跟踪性能。

图2 目标跟踪场景Fig.2 Target tracking scene

图3 飞行速度优化结果Fig.3 Flight speed optimization results
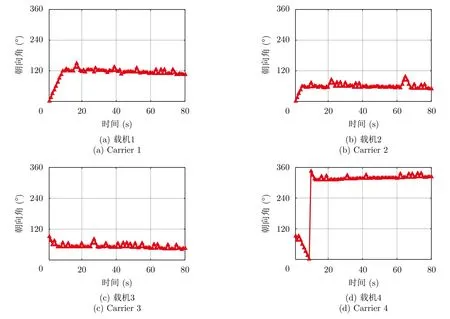
图4 飞行朝向角优化结果Fig.4 Flight heading angle optimization results
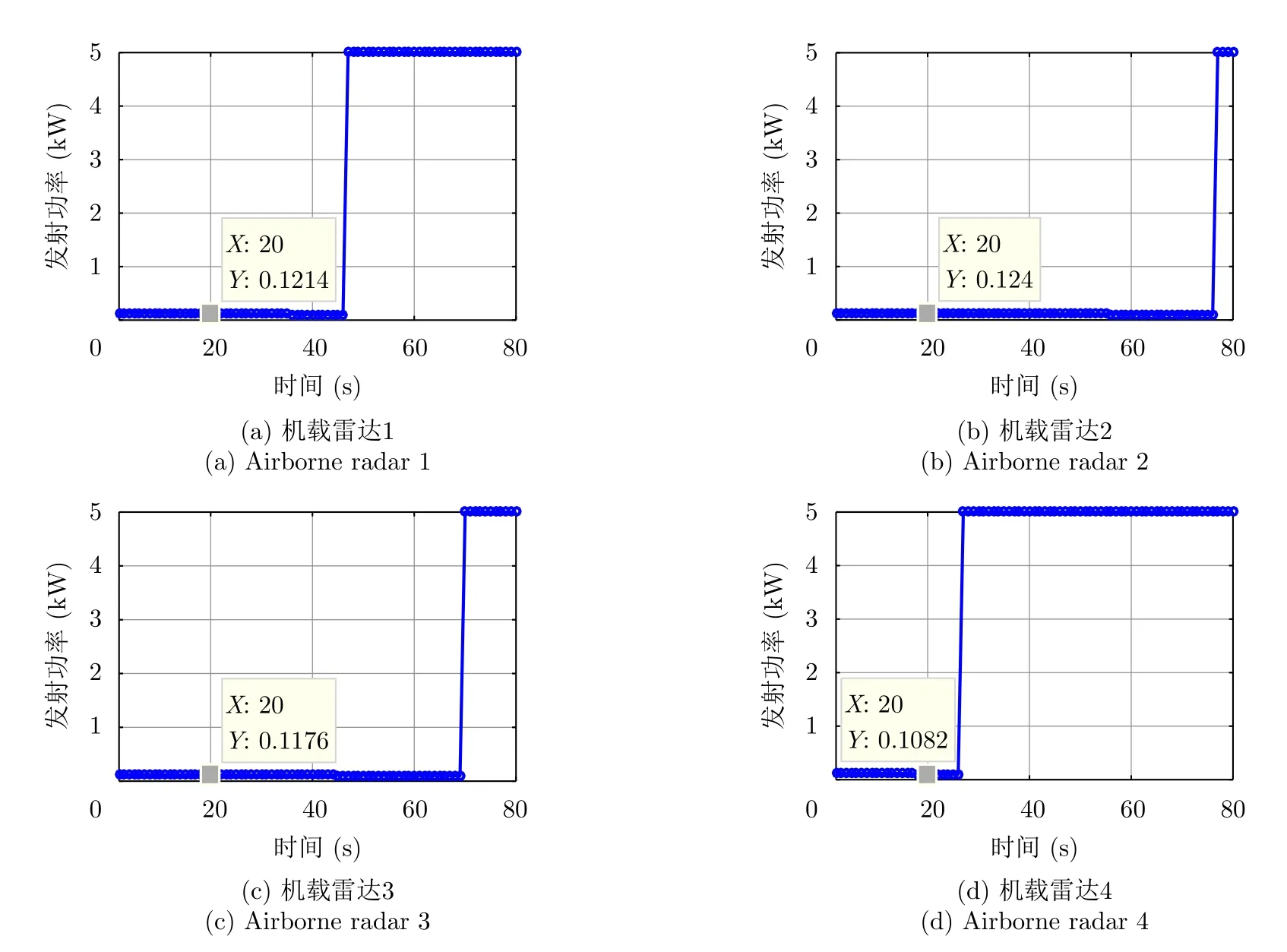
图5 辐射功率优化结果Fig.5 Transmit power optimization results

图6 驻留时间优化结果Fig.6 Dwell time optimization results
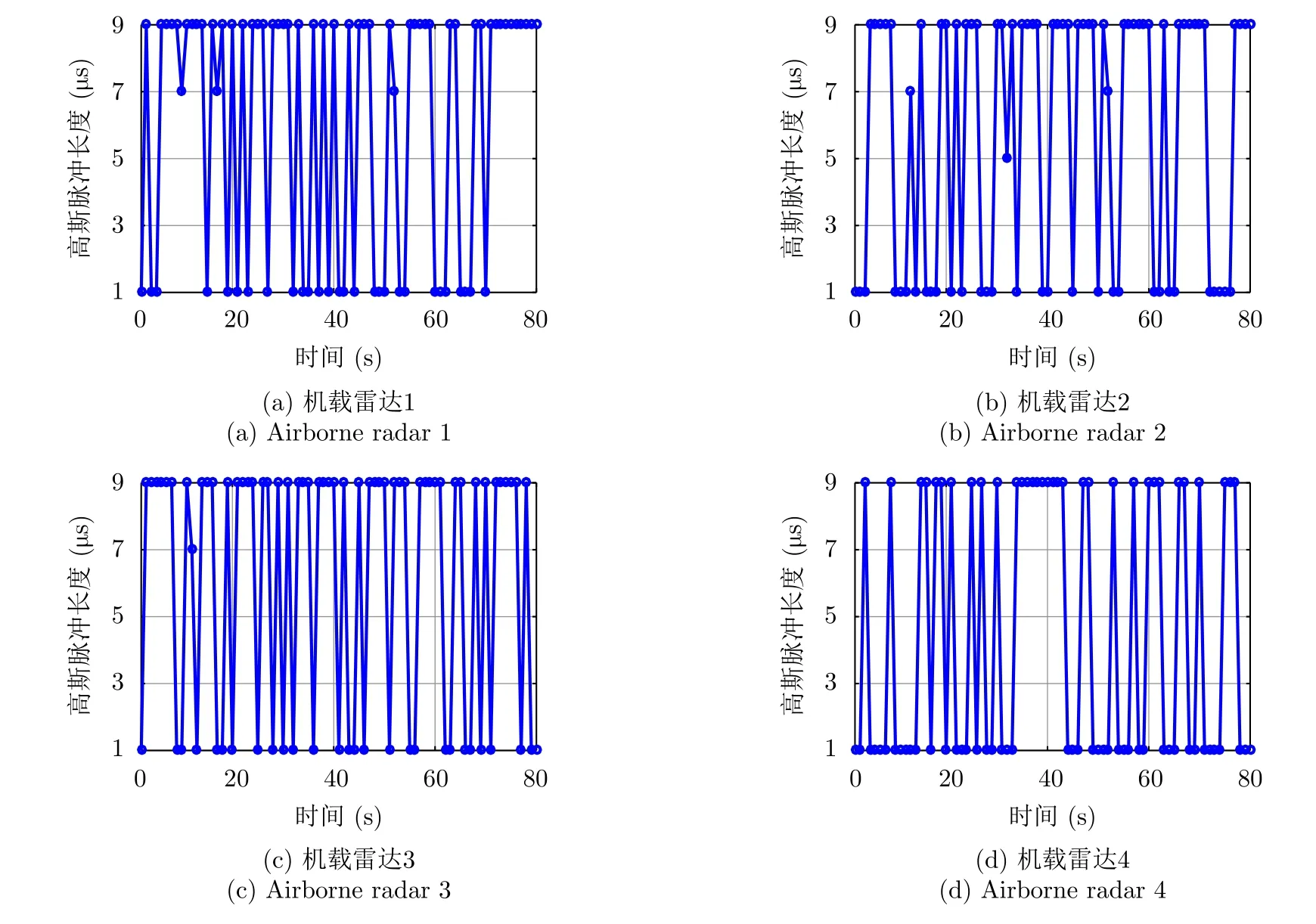
图7 发射信号高斯脉冲长度优化结果Fig.7 Transmit signal Gaussian pulse length optimization results

图8 发射信号带宽优化结果Fig.8 Transmit signal bandwidth optimization results

表4 机载组网雷达初始状态Tab.4 The initial state of airborne radar network
为了进一步验证本文算法的优越性,将所提算法的目标跟踪精度与以下4种算法进行比较:
(1) 机载组网雷达辐射资源和波形参数联合优化算法(Fixed Path Planning and Optimal Transmit Resource Scheduling,FPP-OTRS):固定各载机飞行速度和朝向角,仅优化各机载雷达辐射功率、驻留时间、发射信号高斯脉冲长度和信号带宽。
(2) 机载组网雷达辐射资源和航迹规划联合优化算法(Cooperative Online Path Planning and Transmit Parameter Optimization,COPP-TPO):固定各机载雷达发射信号高斯脉冲长度和信号带宽,仅优化各载机飞行速度、朝向角以及各机载雷达辐射功率、驻留时间。
(3) 机载组网雷达发射波形和航迹规划联合优化算法(Cooperative Online Path Planning and Waveform Parameter Selection,COPP-WPS):固定各机载雷达辐射功率和驻留时间,只优化各载机的飞行速度、朝向角以及各机载雷达发射信号高斯脉冲长度、信号带宽。
(4) 机载组网雷达航迹规划算法(Online Path Planning and Fixed Transmit Resource Scheduling,OPP-FTRS):固定各机载雷达辐射功率、驻留时间、发射信号高斯脉冲长度和信号带宽,只优化各载机飞行速度和朝向角。
定义k时刻目标跟踪的均方根误差(Root Mean Square Error,RMSE)和平均均方根误差(Average Root Mean Square Error,ARMSE)分别为

其中,MC为蒙特卡罗实验次数;Mtot为跟踪过程持续时间;为第n次蒙特卡罗实验时得到的目标位置估计。
图9示出了本文所提算法和上述4种算法的ARMSE对比图。由于FPP-OTRS算法未优化各载机飞行航迹,其所得目标跟踪性能劣于本文所提算法,从而说明了航迹规划能够有效提升目标跟踪精度;由于COPP-TPO算法未优化各雷达发射信号高斯脉冲长度和信号带宽,目标跟踪性能略差于本文所提算法。由此可见,雷达发射信号高斯脉冲长度和信号带宽对于提升目标跟踪精度具有一定影响。由于COPP-WPS算法未优化各机载雷达辐射功率和驻留时间,其目标跟踪性能并不理想,这说明雷达辐射功率和驻留时间对于目标跟踪性能具有较大影响。总的来说,本文所提算法能够在满足预先设定的机载雷达射频隐身性能要求的条件下,通过联合优化设计各载机飞行速度、朝向角等平台运动参数和各部机载雷达辐射功率、驻留时间、发射信号高斯脉冲长度和信号带宽等射频辐射参数,获得相比于其他4种算法更优越的目标跟踪精度。

图9 ARMSE对比结果Fig.9 Comparison results of ARMSE
为了进一步探究被截获概率阈值对优化结果的影响,图10给出了不同被截获概率阈值下目标跟踪RMSE对比。从仿真结果可以看出,随着被截获概率阈值的增加,机载组网雷达的目标跟踪RMSE逐渐减小。这是由于被截获概率在某种程度上约束了机载组网雷达辐射功率和驻留时间,给定的被截获概率阈值越大,机载组网雷达能够获得的辐射功率和时间资源就越多,机载组网雷达的接收信噪比也越大,从而得到更优的目标跟踪精度。
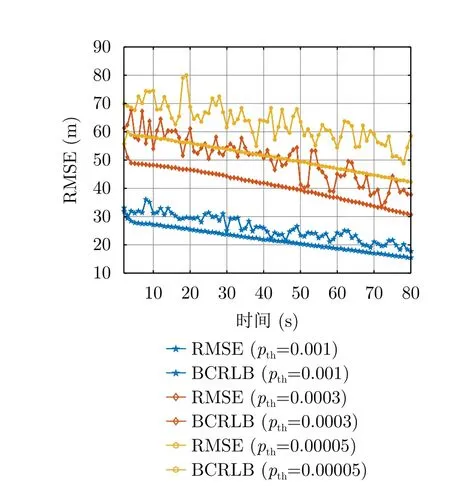
图10 不同被截获概率阈值的RMSE对比结果Fig.10 Comparison results of RMSE with different intercept probability thresholds
5 结语
本文考虑了航迹规划对机载组网雷达目标跟踪精度的影响,提出了一种面向目标跟踪的机载组网雷达辐射参数与航迹规划联合优化算法。针对机载组网雷达,在单目标跟踪场景下,以最小化目标跟踪误差作为优化目标,以满足机载组网雷达射频资源、载机动力学限制和预先设定的被截获概率阈值为约束条件,通过联合优化各载机飞行速度、朝向角等平台运动参数以及各雷达辐射功率、驻留时间、发射信号高斯脉冲长度、信号带宽等射频辐射参数,提升了机载组网雷达的目标跟踪性能。仿真结果表明,本文所提算法能够在满足各部机载雷达射频隐身性能的条件下,有效提高目标跟踪精度。另外,给定的被截获概率阈值越高,机载组网雷达可获得的射频辐射资源就越多,目标跟踪精度也就越高。在实际战场中,可根据具体威胁环境设定被截获概率阈值,从而获得满足作战任务要求的目标跟踪精度。下一步将围绕多目标跟踪场景下机载组网雷达辐射参数与航迹规划联合优化问题进行研究。
附录

其中,Z表示先验信息费希尔矩阵;Vn表示k时刻第n部雷达的数据费希尔矩阵。随后,对式(A-2)进一步推导,可以得到


