采用变分法的遥感影像条带噪声去除
2019-03-08王昶王旭纪松
王昶,王旭,纪松
(1.辽宁科技大学土木工程学院,114051,辽宁鞍山;2.信息工程大学地理空间信息学院,450001,郑州;3.辽宁林业职业技术学院林学院,110101,沈阳)
受遥感载荷探测器成像机理及外界环境影响,遥感影像时常受到条带噪声污染[1-2],因此在对遥感影像进行分析与应用之前,必须去除条带噪声。在过去的几十年里,国内外学者提出了许多去除条带噪声的方法,如基于滤波方法、基于统计匹配方法等。傅里叶变换滤波法[3]及小波变换滤波法[4]是典型的滤波方法。傅里叶变换滤波法通过分析条带噪声的频率,采用合适的滤波器检测并去除条带噪声,但由于很难找到一个能将信号与噪声有效分离的频率,从而导致条带噪声去除不彻底。小波变换滤波法通过确定的阈值及阈值函数来去除条带噪声,但由于阈值选取的不确定性,会导致条带噪声去除不彻底或影像的细节信息丢失。文献[5]提出了一种把小波滤波法与傅里叶滤波法相结合的组合滤波方法,虽然该方法可以有效去除条带噪声[5],但在去除条带噪声时会丢失影像细节。基于统计匹配的方法根据条带噪声行与非条带噪声行灰度统计特性的差异来去除条带噪声。直方图匹配和矩匹配是典型的统计匹配方法,它们分别根据像元灰度的差异及像元灰度矩的差异来去除条带噪声。然而,这类方法过度依赖灰度统计数据集,从而使条带噪声去除不彻底[6-9]。

(a)MODIS 33影像 (b)图1a水平梯度 (c)图1a垂直梯度图1 MODIS 33影像及梯度图
近年来,学者们提出基于变分法来去除条带噪声,如文献[10]根据条带噪声特点建立了一种单向变分模型[10];文献[11]提出了一种单向变分TV(total variation)与框架正则化相结合的模型[11];文献[12]构建了一种单向变分与TV-Stokes相结合的去噪模型[12];文献[13]根据影像具有低秩性及条带噪声具有稀疏性特征构建了条带噪声分离模型[13]。上述变分模型虽然可以在去除条带噪声的同时更多地保留影像细节,但由于模型的正则化强度很难把控,还是会丢失影像细节。
针对条带噪声去除过程中容易丢失影像细节这一问题,本文构建了两种单向变分模型来去除条带噪声。通过构建的条带去除单向变分模型可以初步获得去噪后的近似遥感影像及条带噪声影像,并且避免去噪后的影像出现阶梯效应。为了避免影像细节丢失,通过构建的条带保留单向变分模型可以从条带噪声影像中分离出影像细节。最后,把近似恢复影像与影像细节累加得到去噪影像。
1 条带噪声去除方法
1.1 条带噪声的特点分析
条带噪声是一种结构性噪声,具有单向性及方向性[14]。本文以MODIS(moderate-resolution imaging spectroradiometer)第33波段Level-1B遥感数据为例,并计算其水平方向梯度和垂直方向梯度。从图1可以看到,条带噪声只影响垂直方向梯度(见图1c),而水平方向梯度(见图1b)不受影响。为了显示效果,对图1b、图1c的灰度值进行了线性拉伸。
1.2 条带去除单向变分模型
1.2.1 条带去除单向变分模型构建 经典的单向变分模型是在TV模型的基础上结合条带噪声的特征转变而来的,但由于TV模型在影像平稳区域容易产生阶梯效应,因此首先对TV模型进行改进,建立一种具备同性扩散及异性扩散能力的TV正则化模型,然后在改进的TV模型基础上结合条带噪声特征来构建条带去除单向变分模型。改进的TV模型表达式如下
(1)
式中:U表示去噪后的遥感影像;F表示含条带噪声的遥感影像;V表示条带噪声;λ0表示正则项参数。
式(1)的欧拉-拉格朗日表达式为
2λ0(U-F)-
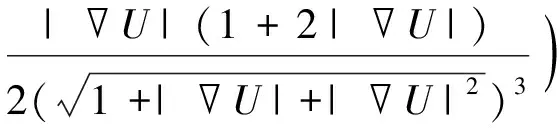
(2)
对式(2)进行扩散能力分析。首先对影像局部结构进行分解,建立直角坐标系(τ,n),从而将式(2)写成
2λ0(U-F)-[T1(|U|)Utt+
T2(|U|)Unn]=0
(3)
式中:Utt和Unn分别表示沿切线和法线方向的二阶导数;T1(|U|)和T2(|U|)分别表示沿切线和法线方向的扩散函数,其控制着沿切线和法线方向的扩散强度
T1(|U|)
(4)
T2(|U|)
(5)
根据式(1)建立条带去除单向变分模型如下
(6)
式中等号右边第1项为保真项,第2项是保持U和F在条带方向梯度一致,第3项表示对条带噪声垂直方向梯度进行惩罚。
1.2.2 方法优化 式(6)对应的欧拉-拉格朗日方程[15-16]为
(7)
将影像定义域Ω离散化,设定x=ik,y=jk,取k=1,则式(7)的离散形式为
λ1(U-f)+D-x(D+x(U-F))+
(8)
式中
(D±xU)i,j=±(Ui±1,j-Ui,j)/k
(D±yU)i,j=±(Ui,j±1-Ui,j)/k
(Dx0U)i,j=(Ui+1,j-Ui-1,j)/2k
(Dy0U)i,j=(Ui,j+1-Ui,j-1)/2k
采用不动点Gauss-Seidel迭代法对式(8)进行求解,得到式(6)的递推公式为
(9)
对影像边界上的点采用Neumann边界条件,即
(10)
式中:i、j分别为列索引和行索引;M×N表示影像U的大小。
1.3 条带保留单向变分模型
1.3.1 条带保留单向变分模型构建 由于无法把控条带去除单向变分模型的正则化强度,因此通过此模型去除条带噪声时会丢失影像细节,而丢失的影像细节包含在条带噪声影像中。为了避免影像细节丢失,构建条带保留单向变分模型如下
(11)
式中:等号右边第1项为保真项,第2项是保持条带噪声影像和条带噪声在水平方向梯度一致,第3项表示对条带噪声水平方向梯度的惩罚;s表示条带噪声;S表示近似条带噪声影像;u表示细节信息。
1.3.2 方法优化 式(11)对应的欧拉-拉格朗日方程为
(12)
将影像定义域Ω离散化,同样设定x=ik,y=jk,取k=1,则式(12)的离散形式为
λ1(s-S)+D-x(D+x(s-S))+λ0D-x(D+xs)=0
(13)
式中D+x、D+y分别表示在x、y方向前向一阶差分算子,D-x、D-y分别表示在x、y方向后向一阶差分算子
(D±xs)i,j=±(si±1,j-si,j)/k
(D±ys)i,j=±(si,j±1-si,j)/k
利用不动点Gauss-Seidel迭代法对式(13)进行求解,得到式(11)的递推公式为
(14)
对影像边界上的点采用Neumann边界条件,即
(15)
2 实验与分析
本文实验选择的4幅遥感影像为:带有随机条带噪声的MODIS第30波段Level-1B遥感数据;带有周期性条带噪声的MODIS第33波段Level-1B遥感数据;带有周期性条带噪声的Landsat TM(thematic mapper)第3波段遥感数据;带有周期性条带噪声的航空影像数据。本文中关于遥感影像条带噪声去除的实现及主客观评价指标的计算均采用Matlab2016软件完成,
执行运算的笔记本电脑是
Inter(R)Core(TM)i5-5200U CPU@2.20 GHz处理器,4 GB内存。
首先,采用条带去除单向变分模型进行条带噪声初步分离,为了显示效果,对条带噪声影像的灰度值进行线性拉伸,实验结果如图2所示。
从图2中可以看到,经条带去除单向变分模型去噪后,分离出的近似MODIS 30影像、近似MODIS 33影像、近似TM影像及近似航空影像都不受条带噪声污染(见图2b、图2e、图2h及图2k),而从条带噪声影像(见图2c、图2f、图2i及图2l)中可以看到,除条带噪声外还包含少量影像细节,说明条带去除单向变分模型在去除条带噪声时丢失了影像细节。
为了避免影像细节丢失,采用条带保留单向变分模型去除条带噪声影像中的细节信息。为了显示效果,对条带噪声影像、条带噪声及细节信息的灰度值进行线性拉伸,实验结果如图3所示。
从图3中可以看到,条带保留单向变分模型可以有效去除条带噪声影像中的细节信息而只保留条带噪声(见图3b、图3e、图3h及图3k),再通过条带噪声影像与条带噪声相减从而获得细节信息(见图3c、图3f、图3i及图3l)。把近似MODIS 30影像、近似MODIS 33影像、近似TM影像及近似航空影像分别与细节信息累加得到去噪影像,并与文献结果[3,7,12,14-16]进行比较。为了显示效果,对不同方法对应的残差图灰度值进行线性拉伸,实验结果如图4所示。
从图4可以看到:经文献[3]方法去噪后,条带噪声被有效去除,但去噪后的影像出现模糊;经文献[7]方法去噪后,条带噪声去除不彻底;经文献[12][14]方法去噪后,虽然条带噪声被有效去除,但由于对影像某些区域的处理过于平滑,从而导致影像对比度下降;经文献[15][16]及本文方法去噪后,不仅可以有效去除条带噪声,而且去噪后的影像视觉效果较好。从不同方法对应的残差图(见图4b、图4d、图4f、图4h)可以看到,本文方法所对应的残差图中只包含条带噪声,基本没有影像细节,而其他方法所对应的残差图中都存在少量影像细节。

(a)MODIS 30 (b)近似MODIS 30(c)近似条带噪声 (d)MODIS 33 (e)近似MODIS 33(f)近似条带噪声

(g)TM (h)近似TM (i)近似条带噪声 (j)航空 (k)近似航空 (l)近似条带噪声图2 含条带噪声的遥感影像初步分离结果示意图

(a)近似MODIS 30 (b)条带噪声 (c)细节信息 (d)近似MODIS 33 (e)条带噪声 (f)细节信息

(g)近似TM (h)条带噪声 (i)细节信息 (j)近似航空 (k)条带噪声 (l)细节信息图3 条带噪声影像的分离结果示意图

(a)MODIS 30条带噪声去除

(b)MODIS 30条带噪声去除残差图

(c)MODIS 33条带噪声去除

(d)MODIS 33条带噪声去除残差图

(e)TM条带噪声去除

(f)TM条带噪声去除残差图

(g)航空条带噪声去除

(h)航空条带噪声去除残差图图4 不同方法的去噪结果及对应的残差图
本文除了主观上采用直观影像视觉效果外,客观上采用影像质量提升因子If[8]及影像扭曲度Id[10]等指标进行评价,并计算各种去噪方法的效率,结果如表1所示。
从表1可以看到,本文方法的If及Id值高于其他对比方法,说明本文方法能在影像扭曲较小的情况下完全去除条带噪声,并且去噪后的影像质量提升程度最大。从不同方法的计算效率来看,文献[3]方法计算时间最短,文献[7]方法最长。由于本文方法是分两个步骤去除条带噪声的,所以计算效率较其他方法低,但高于文献[7][15]两种方法。
3 结 论
为了避免条带噪声去除过程中丢失影像细节,本文构建了一种综合两种单向变分模型的组合条带噪声去除方法,此方法可以有效去除MODIS影像、TM影像及航空影像上的条带噪声。与其他方法相比,本文方法在保留影像细节及影像质量提升两方面都是最优的。

表1 不同去噪方法的客观评价指标统计结果及效率
本文方法虽然在去除条带噪声时能更好地保留影像细节信息,但由于此方法分两个步骤来去除条带噪声,因此会导致计算效率较其他方法低。
