基于二阶线性自抗扰的虚拟同步发电机二次调频控制

葛胜升，王 鹏，施 凯

（1.南京航空航天大学自动化学院，南京 211106；2.芜湖职业技术学院汽车与航空学院，芜湖 241000；3.江苏大学电气信息工程学院，镇江 212013）

随着传统能源的短缺和环境污染的日益加剧，分布式发电由于具有能源利用率高、对环境污染小及能够因地制宜等优点，受到广泛关注。微电网作为分布式发电应用的主要形式，通常分为并网和孤岛两种运行模式，而分布式电源通过逆变器分别与电网和负荷连接。传统的逆变器控制主要有恒功率、恒压恒频和下垂控制等方式[1]，这些控制方式虽然响应速度较快，但它们都有一个共同的缺点，即缺少惯性和阻尼[2]。当遇到负载突变或电网频率扰动时，无法提供电压和频率支撑，从而引起系统电压、频率及输出功率的突变，严重时造成系统解列和元器件损坏[3]。

为解决以上问题，有学者提出将虚拟同步发电机VSG（virtual synchronous generator）技术应用于逆变器控制。该技术充分利用电力电子装置控制的灵活性，采用同步发电机SG（synchronous generator）的转子运动方程和电气方程分别模拟其有功功率和无功电压的输出特性[4]，从而提供主动支撑和阻尼。传统的VSG控制采用下垂控制，通过改变系统的给定输入功率来实现一次调频，但在孤岛状态下，当系统负载突增或负载切入/切出的暂态工况时，单纯依靠改变惯量和阻尼不能完全应对负载的突增、突减，一次调频无法实现系统频率的无差调节，因此需加入二次调频控制。

微电网进行二次调频多采用集中式的控制结构[5]。文献[6]提出基于下垂控制的二次调频控制，根据电力系统的二次调频原理，在VSG有功环的功率与频率的下垂控制中引入积分控制实现频率的无差调节；文献[7]通过分析VSG 的功频特性，提出在VSG的功率下垂环节之前增加PI控制器，能够实现对多台VSG进行二次调频控制，且可根据各机组容量合理分配；文献[8]分析比较了VSG采用工频控制方式在离并网模式下的频率偏差，证明传统VSG控制不适用于孤岛状态，提出将频率偏差引入转子方程，无需降频控制即可实现对频率的无差调节。上述文献所提出的二次调频控制皆为常用的基于PI 控制的二次调频，但当系统携带不同负载时，其控制参数均需重新调节，且系统响应速度较慢。文献[9]提出一种基于VSG 控制的多方参与协同频率控制策略，通过在VSG控制中引入PI控制环节实现二次功率分配，在PI 控制器后加入分配系数，通过自适应调整包括分配系数和功率阻尼系数在内的VSG 参数，实现根据备用容量实时分配功率，但还需借助备用机组，且系统响应速度有限，无法实现快速控制。

自抗扰控制具有抗扰动能力强、动态性能好、控制精度高，以及不需要考虑控制对象的具体模型等优点，能够很好替代传统PI 控制器。文献[10]提出将线性自抗扰控制LADRC（linear active disturbance rejection control）算法与VSG 控制相结合，通过对系统输入功率的控制最终实现系统的二次调频，但其参数过多，参数整定非常困难。本文针对孤岛状态下VSG的运行控制，通过分析系统输出频率的二阶模型，结合二阶LADRC控制算法，提出新的VSG二次调频方法，使VSG在孤岛状态下发生负载突增时，能够实现对系统频率无差调节，达到二次调频的目的。并在Matlab/Simulink 中搭建基于二次LADRC 的VSG 控制模型，验证了所提控制策略的正确性和有效性。

1 VSG 基本原理

图1为VSG的拓扑结构，由图1可知，通过控制三相全桥电压源型逆变器可模拟SG 的输出外特性。其中，逆变器直流侧相当于微电网中的分布式电源，L1、L2分别为逆变器滤波电感和线路电感，C为逆变器滤波电容，即构成LCL型滤波单元；R1、R2分别为等效线路电阻；vabc、iabc分别为逆变器输出电压和电流；Zload为VSG所带负载。

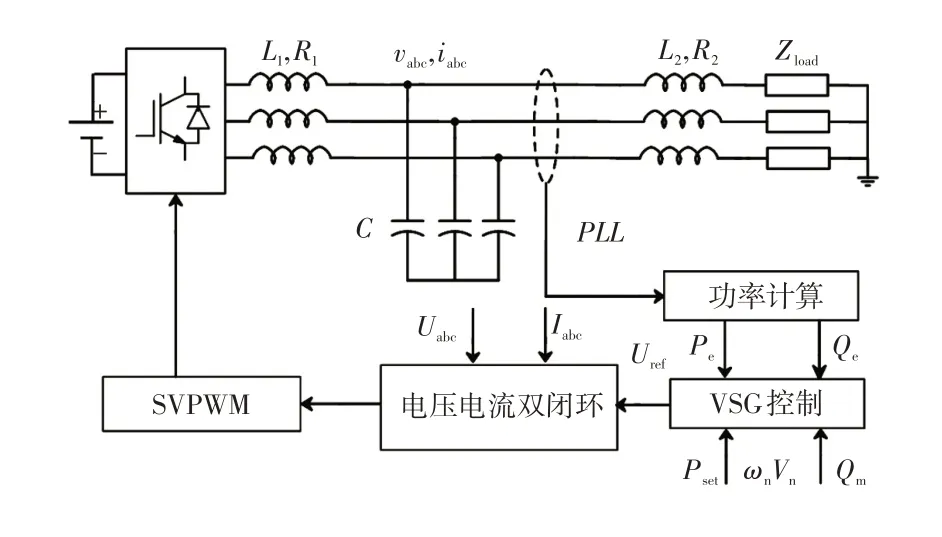
图1 VSG 拓扑结构Fig.1 Topological structure of VSG

通常情况下，为了方便分析，假设SG的极对数为1，则SG的机械角速度与电气角速度相等。根据传统SG的二阶模型，等效的转子运动方程可表示为

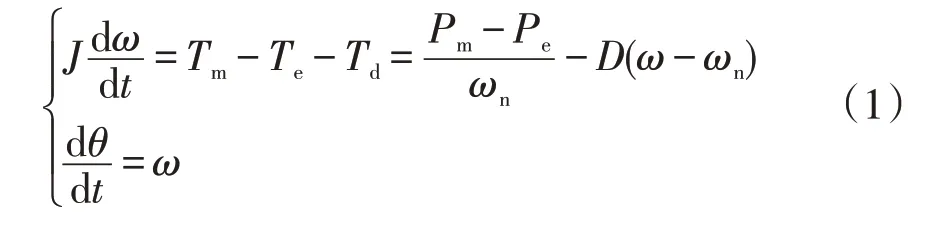
式中：J为虚拟转动惯量；D为阻尼转矩对应的阻尼系数；Tm、Te和Td分别为SG的机械转矩、电磁转矩和阻尼转矩；θ为等效SG的功角；ω、ωn分别为输出角速度和额定角速度；Pm、Pe分别为机械功率和电磁功率。

VSG通过引入虚拟转动惯量J和阻尼系数D模拟SG 的转子惯性和阻尼，同时再引入有功频率偏差反馈环节模拟SG 调速器的功能，可得机械功率Pm为

式中：Pm为系统的有功功率指定值；kf为下垂调差系数。

式（2）对系统的频率稳定性具有非常大的改善作用。但实际系统的三相电压总是存在不同程度的谐波，根据瞬时功率理论，此时测量得到的输出瞬时功率中含有最低频率为两倍工频的脉动分量，这些脉动分量最终导致输出电压发生畸变，影响电能质量。因此在功率测量模块后边需加入一阶滤波器LPF（low pass filter），对功率进行滤波处理，可得电磁功率Pe为

式中：Pout为功率计算模块计算功率；τ为LPF的时间常数。

图2 为VSG 控制框图。由式（1）、（2）可得VSG的有功环控制，即图2中VSG的有功环部分。

VSG 控制的电压-无功控制环节，可通过模拟SG的励磁调节器得到，即

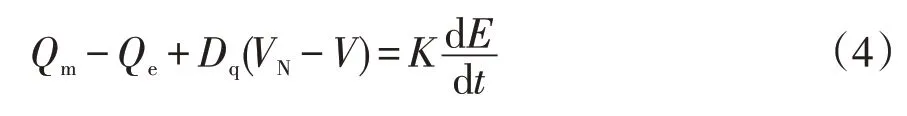
式中：Qm为参考无功功率；Qe为VSG 输出无功功率；Dq为无功调节系数；K为积分系数；V为系统输出电压幅值；Vn为系统额定电压幅值；E为逆变器输出电压基波分量幅值。图2 中的无功环部分通过积分环节来消除电压差，以实现VSG 的动态无功-电压调节。

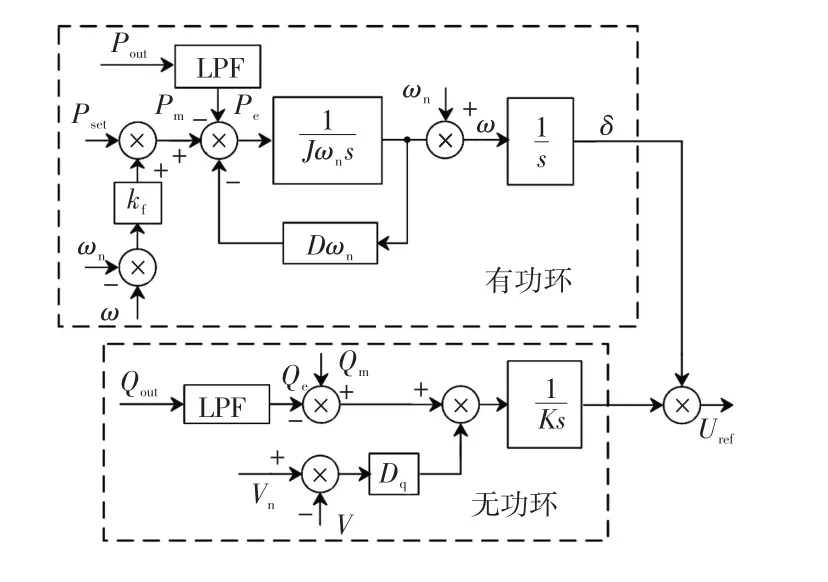
图2 VSG 控制框图Fig.2 Control block diagram of VSG

2 基于自抗扰控制的VSG 二次调频

2.1 自抗扰控制算法

自抗扰控制的控制过程可以描述为不需要了解系统的内部控制对象，将系统的内部和外部扰动均统一做为不确定扰动，而影响这些不确定扰动的因素或参数能够被扩张观测器ESO（extended state observer）观测；状态误差反馈SEF（state error feedback）能够根据观测到的结果对系统进行适当的补偿，降低扰动对系统的影响，以实现对指定参数的跟踪效果[11]。

二阶LADRC系统由ESO和线性状态误差反馈LSEF（linear state error feedback）等部分组成[12]。设线性二阶单输入、单输出系统对象为

式中：u、y分别为系统对象的输入和输出；w为系统的外部扰动；a1、a2分别为系统的参数；b为系统增益，b≈b0[13]，b0为标称值，且a1、a2、b均未知。若 令，设w+(b-b0)u为系统总扰动，其包含系统内部不确定性和外部扰动，则可得式（5）的状态方程为

式中，x1、x2分别为系统的状态变量。

建立LESO的状态方程为

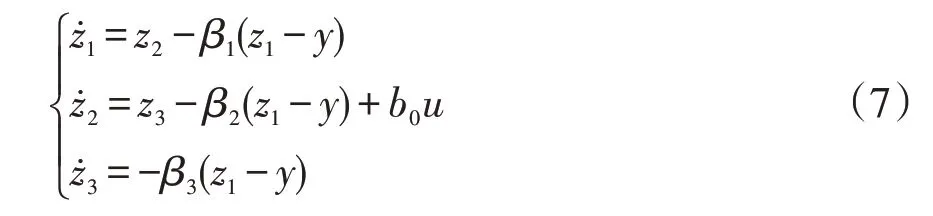
式中：β1、β2和β3均为待定系数；z1、z2和z3分别为控制器中间变量。通过选取合适的观测器增益β1、β2和β3，LESO能够实现式（5）中各种变量的实时跟踪，即

以LESO的输出构成PD控制器，则系统对象的输入u可表示为

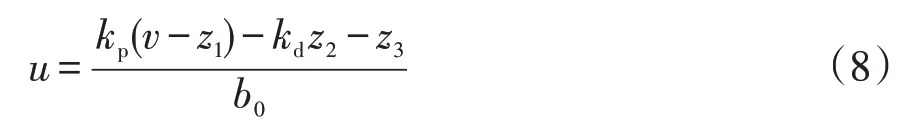
式中，kp、kd为PD 控制器的待定参数，根据文献[14]参数kp、kd可表示为

式中：ωc为控制器带宽；ξ为阻尼比。

LESO的特征方程可表示为

式中，复频率s=jω。选取理想特征方程λ(s)=(s+ω0)3，则有

式中，ω0为观测器带宽[15]。

由此可得LADRC模型如图3所示，其中G（s）为控制对象。

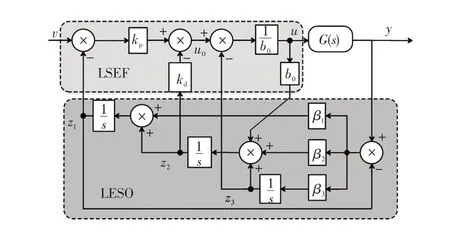
图3 二阶LADRC 模型Fig.3 Second-order LADRC model

由图3及式（8）可得

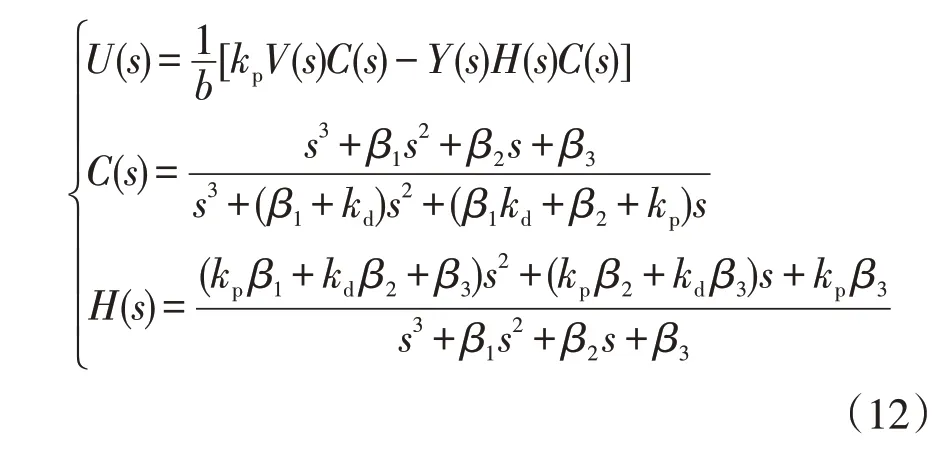
式中，V（s）、Y（s）分别为参考输入信号和被控对象输出在复频域下的表现形式。

由此可得LADRC 的控制框图如图4 所示。图4 中，被控制对象可以表示为，f为集中扰动。

图4 LADRC 控制框图Fig.4 Control block diagram of LADRC

2.2 VSG 的二次调频

2.2.1 基于PI 控制的二次调频

VSG运行于微电网孤岛模式时，由于一次调频特性，当突增负载时，系统的频率会发生降低，对系统稳定性造成影响。图5 为基于PI 控制的VSG 二次调频方法，由图5 可知，在阻尼环节中加入积分器，与阻尼转矩组合成PI 控制器，实现对系统额定频率的追踪，使VSG在孤岛模式下可自动跟踪负荷波动并改变自身的出力，为微网提供频率支撑。

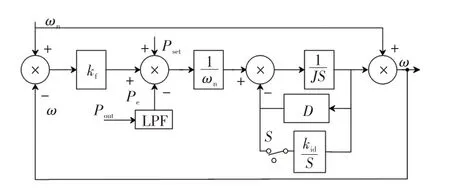
图5 基于PI 控制的二次调频Fig.5 Secondary frequency modulation based on PI control

通过仿真结果可以得到，基于PI控制的二次调频控制方式可实现无差调节，但当携带不同负载时，需重新调节参数，且其反应速度和控制精度并不理想。因此本文提出采用自抗扰控制方式代替其PI功能，并与之进行比较验证。

2.2.2 基于LADRC 控制的二次调频

由图2 中VSG 有功环控制框图可得传统VSG的输出频率与有功功率指令值和系统频率偏差值的闭环传递函数表达式，即

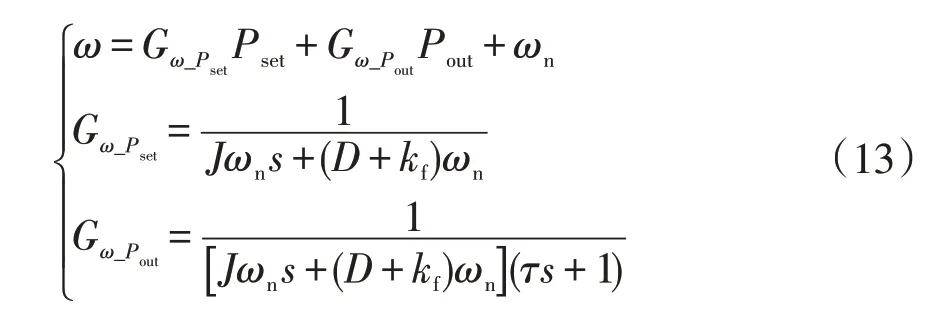
式中，D为阻尼系数。

对式（13）进行拉普拉斯反变换，整理后可得

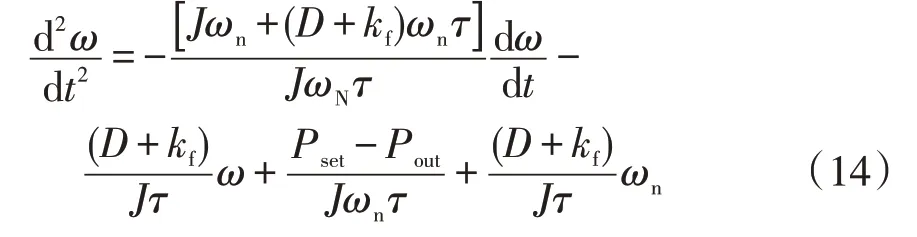
对照式（5）、（13）可将式（14）化简为

因此可得VSG自抗扰控制框图如图6所示。

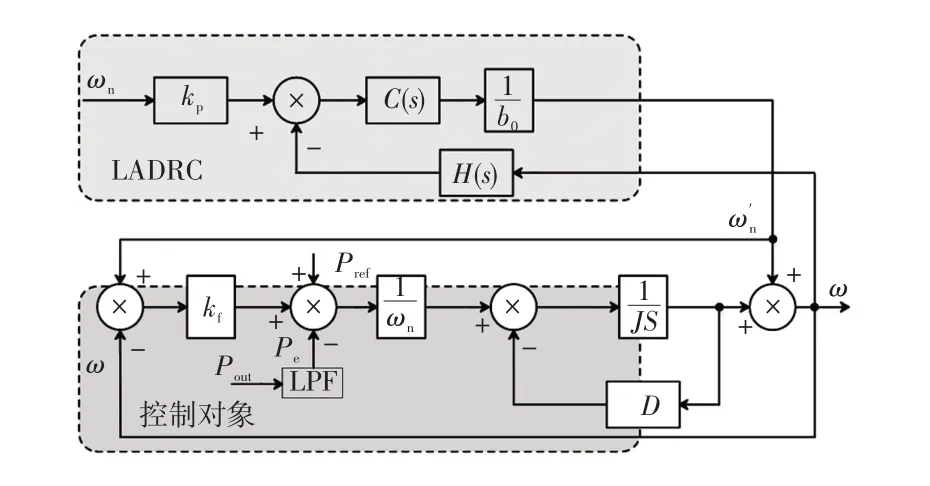
图6 VSG 的自抗扰控制结构Fig.6 Active disturbance rejection control structure of VSG

3 参数确定

控制系统的稳定性是一切控制策略能够实现其优越性的基础，因此使LADRC 控制算法发挥出最优性能的参数选择，必须建立在能够使系统稳定运行的基础之上。因此，对LADRC 中的参数进行整定，根据第2.1节分析，LADRC中还有3个参数b、ωc与ω0待定，由式（13）和式（14）可得b为

运用自动控制理论中的林纳德-奇帕特（Lienard-Chipard）稳定性判定分析可以判断系统是否稳定。其稳定性判定的充分必要条件为系统特征方程中的各项系数及其行列式的奇偶阶数均大于零。运用到本次控制系统中，根据图6推导出闭环传递函数为

式中：ω(s)、Pout(s)、Pref(s)和ωn(s)分别为其在复频域下的表现形式。

可得特征方程为

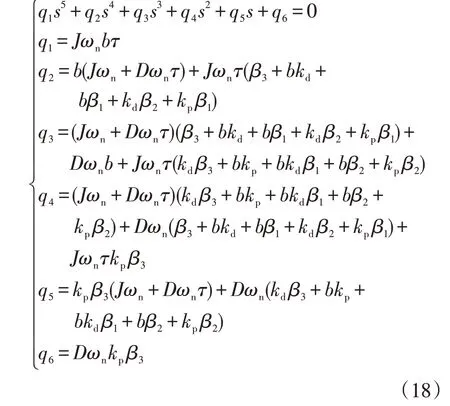
由式（18）可以看出，q1～q6均大于零，因此使系统稳定的条件可简化[16]为

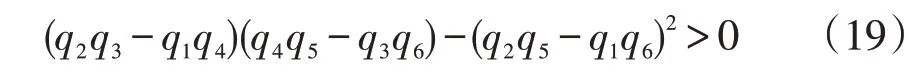
因此，由式（18）的约束，可以在系统稳定时初步确定ωc与ω0之间的关系。然而，Lienard-Chipard 稳定性判据并不能反映稳定性的程度。为了进一步获得可靠的参数，有必要分析不同参数对控制器性能的影响。结合以上分析来讨论ωc与ω0的变化对控制器性能的影响。

图7 为ωc增大时N（s）/Q（s）的零极点，由图7可以看出，随着ωc的增大，闭环极点逐渐远离虚轴，系统的响应速度也随之增加；而极点与虚轴之间的夹角先增大后减小，即表示系统的阻尼是先减小后逐渐增大；在ωc最小时，系统的阻尼最大，意味着若选取的ωc过大，有可能造成系统频率会有较大的超调，或带来高频噪音，影响整个控制系统。图8为ωc增大时的M（s）/Q（s）伯德图。由图8可以看出，随着ωc增大，中频段的相位裕度有明显的提高，系统的抗干扰能力增强，动态性能可得到改善；同时，ωc的增大对低频处的扰动也有了更好地抑制效果。综合分析，ωc取值增大有利于系统保持稳定。因此要使系统实现最优的抗干扰能力，需在满足能够承受系统噪声影响下适量增大ωc。

图7 ωc 增大时N(s)/Q(s)零极点Fig.7 N(s)/Q(s)zero-pole when ωc increases

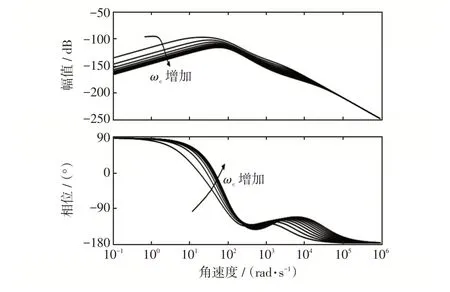
图8 ωc 增大时M(s)/Q(s)伯德图Fig.8 Bode diagram of M(s)/Q(s)when ωc increases

图9 和图10 分别为当ω0增大时N（s）/Q（s）零极点和M（s）/Q（s）伯德图。由图9 可以看出，随着ω0的增加，系统频率和输出有功功率的闭环极点逐渐远离虚轴，ω0的增加也加快了系统的响应速度，使控制系统可以更快地跟踪功率基准。同理，由图10可以得出，随着ω0的增大，系统的抗干扰性能有所提升。因此理论上ω0越大，控制效果越好，但应控制在噪声影响范围之内[17]。

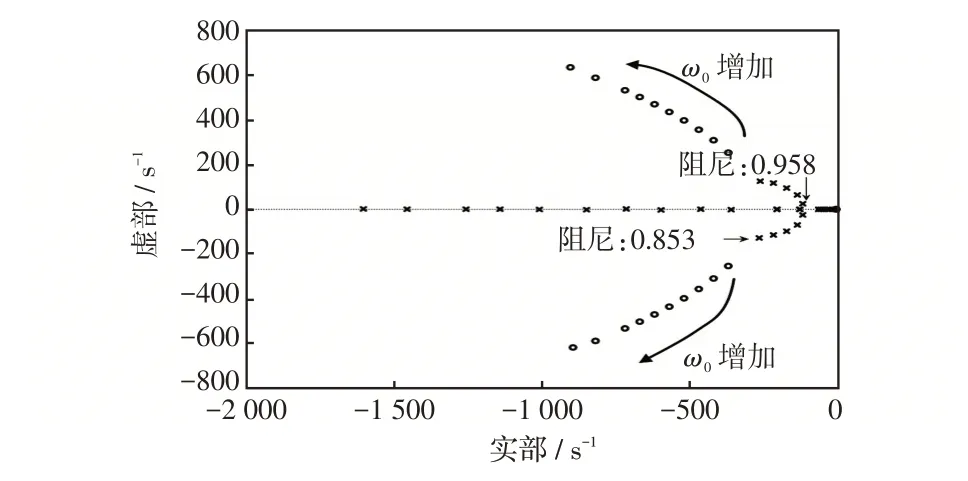
图9 ω0 增大时N(s)/Q(s)零极点Fig.9 N(s)/Q(s)zero-pole when ω0 increases

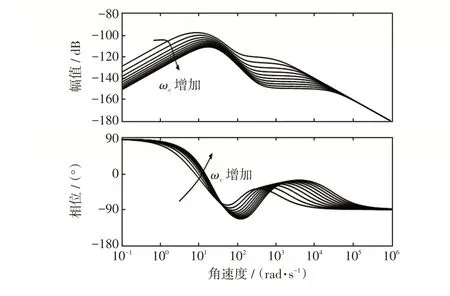
图10 ω0 增大时M(s)/Q(s)伯德图Fig.10 Bode diagram of M(s)/Q(s)when ω0 increases

根据以上分析并结合文献[18]，在选取参数时，首先，按照ωc与ω0之间关系进行参数初值的选择；然后，保持ωc不变，逐步增大ω0，当系统噪声无法满足要求时停止；最后，逐渐增大ωc，当系统噪声造成输出波动较大时减小ω0，继续增大ωc，依次循环调节，以实现最优的控制效果。

4 仿真验证

为验证本文所提出基于二阶LADRC的VSG二次调频控制策略的正确性和有效性，在MATLAB/Simulink 仿真软件平台搭建单台VSG 的仿真模型。仿真系统的主要参数如表1所示。

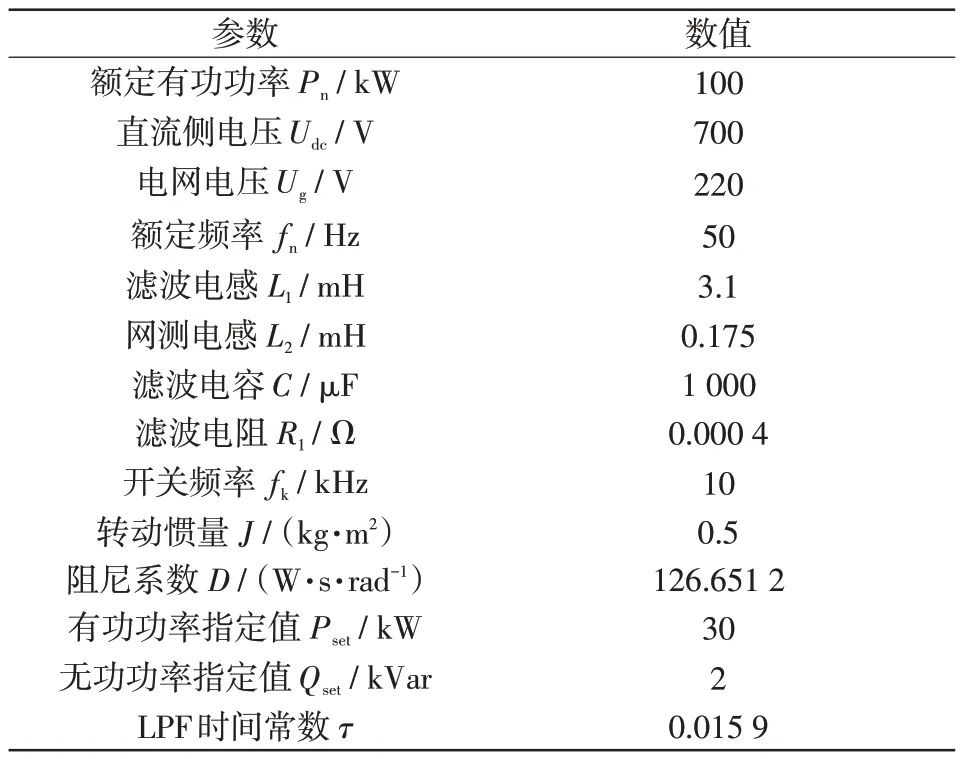
表1 主要仿真参数Tab.1 Main simulation parameters

VSG均处于孤岛运行模式下，VSG的给定有功功率Pset为30 kW，孤岛状态下带30 kW/2 kVar 的负载，当系统运行到0.5 s 时，突增30 kW 的有功负载，并在1 s时切除，整个系统运行时长为1.5 s。

图11 为VSG 处于传统控制策略、PI 调节控制和基于二阶LADRC 控制的系统输出频率比较曲线。由图11 可以看出，当系统负载突增30 kW 时，由于传统控制策略不能实现频率的无差调节，因此系统的输出频率也发生骤降，降低到49.76 Hz，这种现象将对系统中的其他元件造成非常大的伤害；基于阻尼PI 调节的VSG 控制策略虽然能够实现系统的无差调节，但这种控制策略的控制速度较慢且会出现较大的超调现象，恢复时间和超调幅值分别为0.17 s和0.18 Hz；而本文所提出的基于二阶LADRC控制策略的系统输出频率恢复时间和超调幅度仅为0.09 s和0.04 Hz，能够迅速的实现系统的无差调节，相对其他两种控制策略有较大的优势。

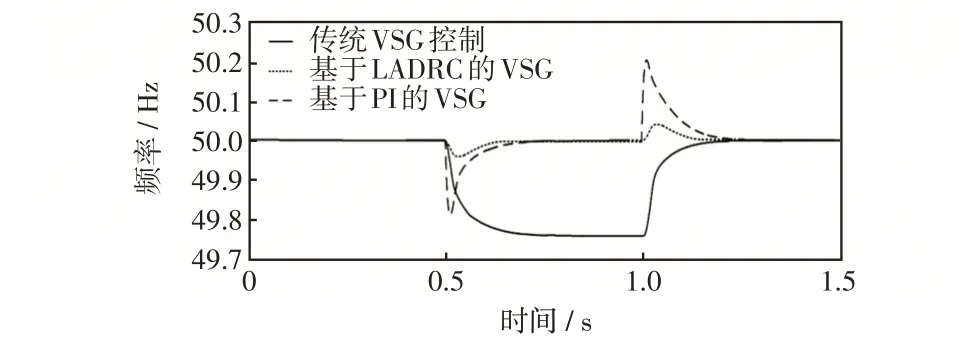
图11 不同控制策略下VSG 的输出频率Fig.11 Output frequency of VSG under different control strategies

图12 为3 种不同控制策略下VSG 的系统输出有功功率对比曲线。由图12 可以看出，传统VSG控制系统输出有功功率的恢复速度较慢；基于PI控制的VSG输出有功功率恢复次之，约为0.12 s；而基于二阶LADRC控制的VSG输出有功功率恢复的最快，约为0.05 s。由此可以得出采用二阶LADRC控制策略有较大的优势。

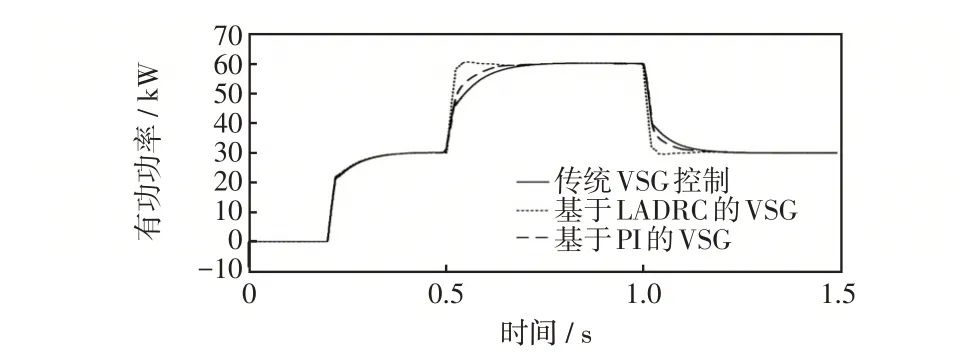
图12 不同控制策略下VSG 的输出有功功率Fig.12 Output active power of VSG under different control strategies

图13～16 为所提新控制策略的中间状态参数u，z1，z2，z3的变化情况。

图13 中间状态参数uFig.13 Intermediate state parameter u

图14 中间状态参数z1Fig.14 Intermediate state parameter z1

图15 中间状态参数z2Fig.15 Intermediate state parameter z2

图16 中间状态参数z3Fig.16 Intermediate state parameter z3

5 结语

针对VSG 孤岛运行时负载突变引起的频率波动，提出一种基于二阶LADRC 的二次调频新方法。首先，利用二阶LADRC的优点取代PI控制器，将其与VSG控制算法相结合，通过对系统输入功率的控制最终实现频率的无差调节。然后，利用Lienard-Chipard 稳定性判据在满足系统稳定性的基础上，通过伯德图分析和验证ωc与ω0的变化对控制器性能的影响，最终确定最优参数。最后，在MATLAB 中搭建仿真模型，并将传统VSG 控制、PI 调节控制和基于二阶LADRC 控制进行仿真和分析对比，仿真结果验证了所提控制策略的正确性和有效性；当负载发生突增、突减时，基于二阶LADRC 的VSG控制方法能够更好地实现二次调频。