基于FPGA 考虑控制特性的光伏直流发电系统暂态实时仿真

王守相，何汝训，张春雨，赵倩宇

（1.天津大学教育部智能电网重点实验室，天津 300072；2.天津市电力系统仿真控制重点实验室，天津 300072）

随着有源配电网中分布式电源的大量接入，电气设备模型日益复杂。为保障新型电力系统的安全稳定运行，针对分布式电源及电力系统架构的实时仿真研究受到了越来越多的关注。

目前，主流的商业实时仿真器底层计算硬件均是以DSP、CPU[1]等为主，本质上它们仍属于全定制电路，处理器内部为串行运作，其计算速度及小步长实时仿真会受到限制。现场可编程门阵列FPGA（field-programmable gate array）因其具有高度的硬件并行性、内存分布性及流水线架构，可以在进行有源配电网精细化仿真的同时提高电力系统与电力电子研究的效率，实现电力系统或电力设备的半实物测试。目前，FPGA 在分布式发电系统暂态实时仿真中展现出巨大潜力[2]。

许多学者对分布式电源系统仿真展开了研究。文献[3-5]利用Simulink、PSCAD 等离线仿真软件，对分布式电源做了大量的研究，但和暂态实时仿真中的环境还有所差距，需要硬件在环技术进行验证与分析；文献[6]对光伏发电系统进行暂态实时仿真分析，搭建了基本仿真框架，但未涉及对光伏系统控制策略的优化研究；文献[7]基于FPGA 对风力发电系统进行了硬件在环仿真，提出一个具有自抗扰控制的功率跟踪策略；文献[8]针对配电网的电气系统进行FPGA 暂态实时仿真，未涉及非线性控制系统；文献[9]研究了基于多FPGA 的电力电子实时仿真系统，但建模方式仅针对特定的电路拓扑，所建模型无法重复利用。

在分布式电源系统仿真中，光伏发电系统的最大功率跟踪MPPT（maximum power point tracking）也是其中一个重要的研究方向。文献[3]提出了改进型变步长跟踪技术，该算法对采样速度和精度要求较高，若跟踪过程中环境连续变化，容易产生误判现象；文献[4]将MPPT 算法和功率预测算法相结合，虽减少了误判次数，但最大功率点仍存在振荡问题；文献[5]提出了基于径向基神经网络的MPPT算法，提高了跟踪精度，但遇到环境突变时易陷入局部功率最优。

综上，本文基于FPGA 平台搭建了光伏独立直流发电系统实时仿真器，提出误差反向传播BP（back propagation）神经网络与恒压控制法CVT（constant voltage tracking）、功率扰动法P&O（perturbation and observation）相结合的自适应最大功率点跟踪AMPPT（adaptive maximum power point tracking）技术，并对光伏电源特性和电力电子设备模型进行研究，同时验证了多种光伏控制策略在FPGA实时仿真器中的实际运用效果。

1 基于FPGA 的电气系统建模设计

1.1 光伏电池建模

光伏电池是光伏系统的基本构成单元，为了适应工程研究的需求，其等效模型可以采用4参数工程模型[4]来描述。本文在文献[4]的基础上对光伏工程模型进行优化处理，推导出适用于FPGA 架构的光伏组件输出特性方程为

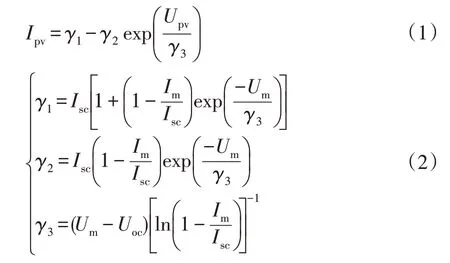
式中：γ1、γ2和γ3为系统结构参数；Upv、Ipv分别为光伏电池的输出电压和输出电流；Isc、Uoc、Um和Im分别为光伏电池短路电流、开路电压、最大功率点电压和最大功率点电流，通常由厂商提供。

考虑光照及温度变化，需要对参数加以修正来描述新的光伏输出特性方程。设一般工况与标准工况下的相对光照强度差ΔS和相对温度差ΔT为

式中：S为光照强度；T为环境温度；Sref为标准光照强度，Sref=1000 W/m2；Tref为标准温度，Tref=25 ℃。

式中：a为电流温度系数，a=0.002 5 ℃；b为电压光照系数，b=0.000 5 ；c为电压温度系数，c=0.002 88 ℃；e为自然对数的底数。

将式（4）中所修正的光伏参数代入式（1）、（2），可得新的光伏输出特性方程。基于FPGA的光伏组件模型如图1 所示。为模拟光伏组件工作状态下的不同应用场景，可设置多组光照及温度条件，每组场景条件由一组γ1、γ2、γ3参数相对应。在上位机编译过程中，多组γ1、γ2、γ3参数提前求得存于寄存器中，可由FPGA流水线式直接调用，降低了资源消耗量及求解时间，同时提高了整个光伏模型求解速度。

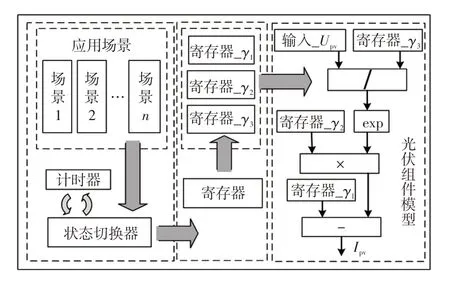
图1 基于FPGA 的光伏组件模型Fig.1 Photovoltaic module model based on FPGA

1.2 电力电子开关建模

目前电力电子设备仿真中常用的双电阻开关模型[10]虽然简单易于实现，但每次开关动作后需要重新形成系统等效导纳矩阵及其因子表，给FPGA实时仿真带来存储和计算压力。

本文采用基于小电感/小电容（L/C）的等效开关模型[11]，即利用小电感L和小电容C分别等效导通和关断状态下的开关器件，通过合理的L、C参数设置，可以在仿真过程中保持系统导纳矩阵不变。由欧拉法差分得到的开关S 断开和闭合时的特性方程可表示为

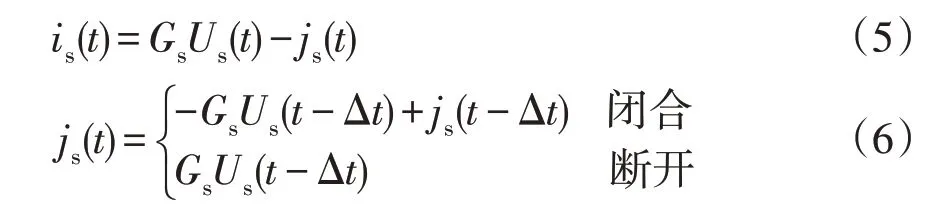
式中：is(t)为开关电流；Gs为开关等效导纳；Δt为仿真步长；Us(t)、Us(t-Δt)分别为本时步和上一时步开关电压；js(t)、js(t-Δt)分别为本时步和上一时步历史量电流源。

对开关元件的仿真，可利用FPGA 高度的硬件并行性及内存分布性，并结合式（6）以搭建开关元件历史量求解模型为例进行说明。基于FPGA的开关元件历史量模型如图2所示，图2中，ROM为只读存储器，RAM 为随机存储器，两者均通过FPGA 上的存储器（M9K）配制而成；RAMs和RAMjs(t)分别存储开关电压和历史量电流源；ROMs_open和ROMs_closed分别存储开关等效导纳和其相反数；寄存器register存储脉宽调制PWM（pulse width modulation）信号；Delay1和Delay2为延时模块。

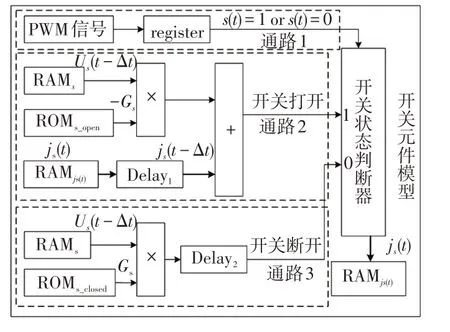
图2 基于FPGA 的开关元件历史量模型Fig.2 Model of switching history based on FPGA

历史量求解模型共分为3 个通路：通路1 为PWM 信号通道；通路2 为开关闭合通道；通路3 为开关断开通道。启动信号触发时，首先，通路2 和通路3 分别从存储器中同时读取us(t-Δt)、-Gs和Gs，并通过2 个浮点数乘法器同时进行乘法运算。然后，通路2 进行下一步浮点数加法运算，为与通路2 中的输出结果js(t)open保持数据对齐，通路3 中的输出结果js(t)closed需延时7 个时钟周期读取。最后，开关状态判断器通过判断通路1的PWM信号状态，确定通路2、3 的开闭，并将处理结果js(t)存入RAMjs(t)中，用于下一时步的计算。其中，js(t-Δt)由js(t)延时一个步长Δt读取。

在模型的硬件实现方式中，3 个通道同时独立并行，从读取数据、代数运算等基本操作环节利用底层并行性及流水线架构，体现了FPGA 的运算速度优势。

2 基于FPGA 的控制系统建模设计

2.1 控制系统典型模块建模

控制系统的元件有特定的输入输出关系，以图3中的CVT模型为例进行基于FPGA的控制系统建模说明。其中，Upv(t)、Ipv(t)分别为光伏电池的输出电压值和输出电流值；Upvref(t)为光伏电池的参考电压。CVT法模型回路以串行求解为主，各个模块之间均按照①PI环节；②限幅环节；③PWM调制环节的控制系统顺序进行求解，但各环节底层子模块功能的实现过程可充分运用空间并行性。

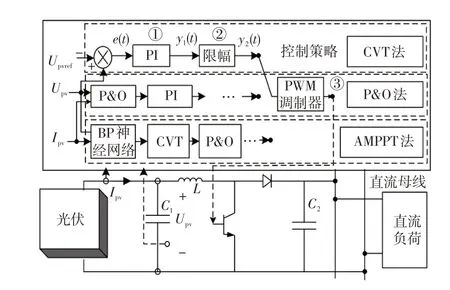
图3 光伏系统示意Fig.3 Schematic of photovoltaic system

2.1.1 传递函数环节

在FPGA仿真器中，可以把连续的控制系统转化为对各个控制元件的显式求解。首先对PI环节进行离散化处理，使用欧拉积分法后的离散化表达式为

式中：e(t)=Upv(t)-Upvref(t)；s为复频率；Kp、Ki分别为比例系数和积分时间系数；M(t-Δt)为累加和。

对y1(t)进行限幅处理，限幅逻辑可表示为

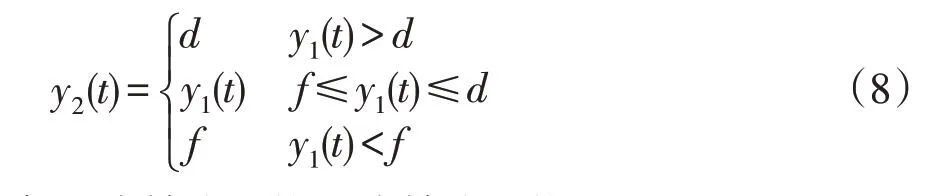
式中：d为输出上限；f为输出下限。

基于FPGA 的传递函数求解模型如图4 所示。图4 中，比例和积分环节采用两通路并行运算，积分环节通过插入一个步长Δt的延时加以解耦，实现不断累加积分；限幅环节通过调用FPGA 的2 个比较器同时进行大小比较，得到最终y2(t)需要消耗2 个时钟周期时间；比较器的实现方式具有高度流水线架构，在处理第1 个比较单元时，后续比较单元的处理也在同时开始进行，其输出时间依次相差1 个时钟周期，体现了FPGA 的数据流动性和空间并行性；为保证精度，控制环节所涉及到的代数运算全部采用32位浮点数，并均可调用FPGA的IP核进行运算，以提升FPGA的运行工作效率。

图4 基于FPGA 的传递函数模型Fig.4 Transfer function model based on FPGA

2.1.2 PWM 调制环节

PWM调制环节是光伏控制系统中的重要组成部分，主要负责开关元件控制信号的生成，其难点在于生成载波信号。文献[6]基于有限状态机，利用计数器和幅值的乘积在每个时步生成载波信号，对FPGA 的数字信号处理DSP（Digital Signal Processing）模块资源提出更高的要求。考虑到载波信号的初始相位，采用读取FPGA中的ROM存储数据进行信号发生器设计。

基于FPGA的载波发生器如图5所示。该载波发生器首先将载波信号根据仿真步长离散化，设电力电子器件开断周期为仿真步长的n倍，即在一个周期内载波可被离散为n个均点；然后，将n个均点的载波幅值数据存储在ROM 中，并设置对应地址为[0：n-1]；最后，地址搜寻器以流水线形式循环搜索ROM地址，形成周期性载波信号。

图5 基于FPGA 的载波生成模型Fig.5 Carrier generation model based on FPGA

2.2 基于BP 神经网络与CVT 法、P&O 法相结合的AMPPT 模型

传统的MPPT控制算法无法兼顾追踪速度与精度[12]，本文提出一种基于BP 神经网络与CVT 法、P&O法相结合的AMPPT 技术。首先，利用BP 神经网络进行先行寻优，以初步定位最大功率点；然后，结合CVT法的启动优势，以最快速度逼近该最大功率点；最后，利用小步长P&O 法在该最大功率点邻域上爬坡搜寻，提高功率跟踪的响应速度和精度。

利用Python 软件搭建BP 神经网络模型，使用温度T、光强G和测试得到的最大功率点构建数据集，采用BP算法对模型参数进行学习，模拟出光伏非线性系统。模型以平均绝对值作为误差函数进行网络训练，缩小预测功率点与真实点之间的误差，使网络趋于收敛。为兼顾模型的预测精度及FPGA 的运算效率，经测试后隐含层大小为10 时，此模型性能最佳。最后将所得到的BP神经网络模型搭载至FPGA 仿真器中，再配合CVT 法、P&O 法进行二次寻优，便可以进行自适应追踪。

3 电气系统与控制系统的信息交互

3.1 电气系统与控制系统的运行流程架构

电气系统与控制系统的运行流程如图6所示。

图6 电气系统与控制系统的运行流程Fig.6 Operation flow of electrical system and control system

光伏电气系统与控制系统采用解耦并行计算，同时需要设计有限状态机FSM（Finite-state machine）去控制各个模块的有序运行。本文在FPGA顶层设计了一个全局时序控制器FSM0，用以精准控制电气系统FSM1和系统FSM2的交替求解，而各个模块及底层子模块又由其子系统时序控制器所约束。

以图6 中的时序控制器FSM1 为例，利用有限状态机设置了5 种电气系统运行状态。①IDLE 为初始状态；②case1为光伏求解模块；③case2为网络电压电流求解模块；④case3 为历史量电源求解模块；⑤case4为开关元件判断模块。每种运行状态均设置各自使能端clken，当clken=1时，该状态开始动作；当clken=0 时，该状态运行结束。state1～state4为控制系统状态。当FPGA处于IDLE状态时，复位信号reset=0，系统处于初始化状态；当系统检测到reset=1，clken1=1时，系统立刻进入case1状态；求出光伏电流后，clken1=0，clken2=1，系统立刻进入case2状态；以此类推，当clken4=0，clken1=1时，系统会重新进入case1状态，进行下一个步长的仿真。

3.2 电气系统与控制系统的时序交互

图7为电气系统与控制系统的交互求解时序。

图7 电气系统与控制系统的交互求解时序Fig.7 Sequence of interactive solution for electrical system and control system

在图7 中，Δt0为电气系统解算时间，Δt1为控制系统解算时间。在实时仿真中，控制系统和电气系统解耦独立运算，其解算时间往往不一致。对于大规模配电网系统，框架节点多，电气系统解算时长可能会大于控制系统，即Δt0＞Δt1，如图7中②所示；由于多分布式电源及电力电子开关复杂多样，会存在解算控制系统规模过大的情况，控制系统解算时长可能会大于电气系统，即Δt0＜Δt1，如图7中③所示；在基于FPGA暂态实时仿真中，可通过延时使电气系统和控制系统的解算时序保持一致，如图7 中①所示。从系统仿真的有序性考虑，电气与控制系统的解算时间Δt的选择可表示为

由图7 和式（9）可知，控制系统和电气系统的交互求解是一个离散交替的过程，将这样的过程持续下去即可完成整个系统的仿真。

4 算例验证

4.1 仿真算例

在图3 所示系统算例中，设置MPPT 的采样时间为0.001 s，PWM 发生器模块的频率为10 kHz。为验证仿真的实时性及准确性，将FPGA 仿真器和离线仿真软件Simulink、PSCAD 作对比，并保持仿真步长一致，统一设为2 μs。

（1）采用CVT法进行测试。保持光伏系统温度T=25 ℃不变，光照强度初始值为1 000 W/m2，在0.06 s 时突降至800 W/m2；在0.08 s 时由800 W/m2突升至1 000 W/m2。将FPGA 仿真结果和PSCAD、Simulink 软件作对比，光伏系统跟踪到的输出功率波形如图8所示。

图8 CVT 法功率跟踪波形Fig.8 Waveforms of power tracking by CVT

（2）采用P&O 法进行FPGA 仿真器测试。测试环境保持与CVT 法一致，则P&O 法跟踪到的输出功率波形如图9所示。

图9 P&O 法功率跟踪波形Fig.9 Waveforms of power tracking by P&O

（3）采用自适应AMPPT 跟踪法。本次测试加入显著的环境因素扰动，将光照强度从1 000 W/m2陡降至600 W/m2，其余测试环境不变，光伏跟踪到的输出功率如图10所示。

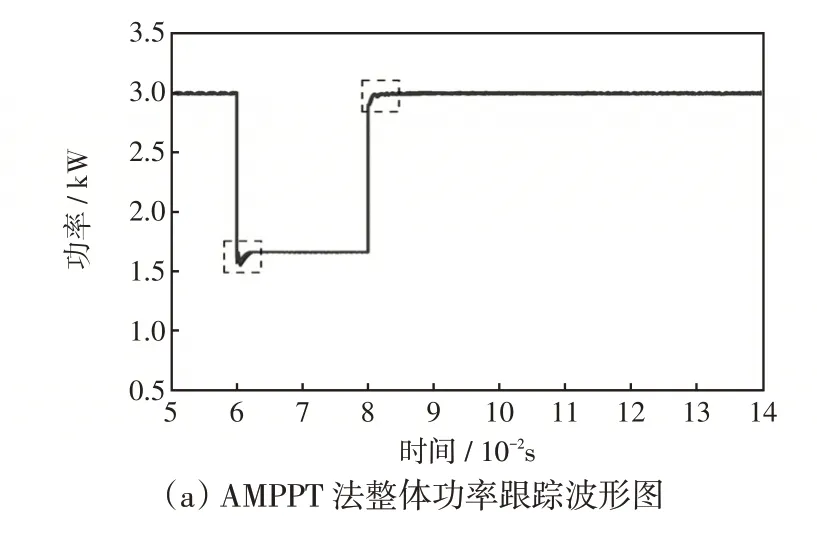
图10 AMPPT 法功率跟踪波形Fig.10 Waveforms of power tracking by AMPPT

4.2 结果分析

在仿真精度方面，图8～10给出了FPGA实时仿真器与商业软件PSCAD、Simulink 离线仿真结果的比较。由图8～10可以看出，在三种不同的MPPT控制策略下，3个仿真系统的输出功率曲线基本重合；在0.6 s 及0.8 s 环境扰动情况下，仿真结果也几乎一致，从而验证了FPGA仿真器的仿真精度。

在仿真控制策略方面，图11 为CVT、P&O、AMPPT三种方法的效果对比；表1为三种方法跟踪所消耗的时间。由图11及表1对比分析可知，CVT法能够快速追踪到最大功率点，稳态精度良好，但参考电压固定，输出功率达不到最大值；P&O 法存在功率振荡现象，环境突变会造成较大功率浪费；自适应AMPPT 寻踪方法动态响应速度较快，过渡到稳态阶段所需时间最短，并且稳态跟踪精度高，减小了跟踪过程中的能量损耗，使光伏系统准确、快速及稳定地工作在最大功率点处。

图11 基于FPGA 的CVT、P&O、AMPPT 效果对比Fig.11 Comparison of effects based on FPGA among CVT,P&O and AMPPT

表1 跟踪所消耗时间Tab.1 Time consumption of tracking ms

5 结语

为保障新型分布式电源系统的安全稳定运行，开发高精度、小步长的实时仿真工具成为必然趋势。本文研发了基于FPGA的光伏实时仿真器，充分展现了FPGA 在仿真精度、仿真速度上的优势及潜力。此外，所提出的自适应AMPPT追踪技术，减小了功率损失，使动态响应速度快、稳态跟踪精度高。该实时仿真模型架构，也同样适用于其他分布式发电系统，为基于小步长的实时仿真奠定了基础。