在小学数学教学中渗透分类思想例谈——以“数学广角——搭配（二）”教学为例

哈尔滨市花园小学 孙 宁

数学课要使学生真正理解和掌握基本的数学知识与技能、数学思想与方法，得到必要的数学思维训练，获得广泛的数学活动经验。小学数学课堂一项重要的内容就是数学思想方法的渗透，而分类思想又是其中尤为重要的思想方法之一。教学中渗透分类思想，不仅可以培养学生有顺序地、有层次地、全面有逻辑性地思考，还能培养学生良好的数学思维品质。从知识的层面而言，发展分类思想能让学生由浅入深不断地分类学习，既要把握全局，又能细致入微，形成系统的认知结构。

以三年级下册“数学广角——搭配（二）”例1的教学为例，研究如何在教学中有效渗透分类思想，让学生在类比、分析、概括中实现对分类思想的运用。

1.教学目标

（1）掌握排列两位数的简单方法，会用四个数字组成没有重复数字的两位数。

（2）经历探索简单事物排列规律的过程，体会分类思想，培养有序思考的习惯，提升观察推理的能力。

（3）感受数学与生活的紧密联系，激发学生学好数学的信心，培养学生从数学的角度看待周围事物，提升全面思考问题的意识。

2.设计理念

借助问题情境、新旧知识联结、自主探究式学习促进学生思考交流，用画图列表等方式直观呈现解决问题的方法，在思维碰撞中不断感受提升，将学生思维引向深处，逐步掌握有序、全面思考问题的方法。

3.上挂下联

教材中这部分内容是在二年级上册“数学广角”的基础上进行学习的，学生已初步接触了一些简单的排列和组合内容，初步感受了排列组合的思想和方法。本单元的例1教学，引导学生尝试稍复杂的排列，这里的例题不仅排列的数字多了1个，而且还增加了“0”这个特殊的数字，体现思维的有序性和全面性，渗透分类思想。

4.教学活动

（1）复习旧知，引入新课

师：前面我们学习过简单的数字组合，你们还记得吗？课前老师要考考你们，请想一想用1、3、5 这三个数字能组成多少个没有重复数字的两位数？

生：可以组成的两位数有13、15、31、35、51、53 六个数字。

师：你们是怎么做到准确又没有遗漏呢？

生：可以先确定十位上的数字，个位上的数字逐一替换，如十位上是1，个位可以是3或5，组成的两位数是13和15。

师：同学们真不简单，把几个数字进行有序排列，就能产生不同的数字，今天我们继续来研究有关数字组合的问题。（板书课题：数学广角搭配例1）

数学是有结构的，有系统的，更是有机的整体，复杂的知识中一定会有内在联系。例1的内容对学生来说还是比较抽象，距离二年级的学习也间隔较远，此时学生解决这类问题的经验和方法，依然停留在二年级具体操作的层面上。因此整节课在导入部分，教师有意识地从二年级数字排列问题入手，引导学生回顾旧知，用1、3、5 这三个数字组成没有重复的两位数。在这样的活动中唤醒学生已有认知，找到学生学习最近发展区，从而为数学排列中有0的问题做铺垫。

（2）自主探索，合作交流

活动一：展示排列，体会有序

出示例1：用数字0、1、3、5能组成多少个没有重复数字的两位数？把你想到的数字写下来。

（学生自主尝试，教师巡视。）

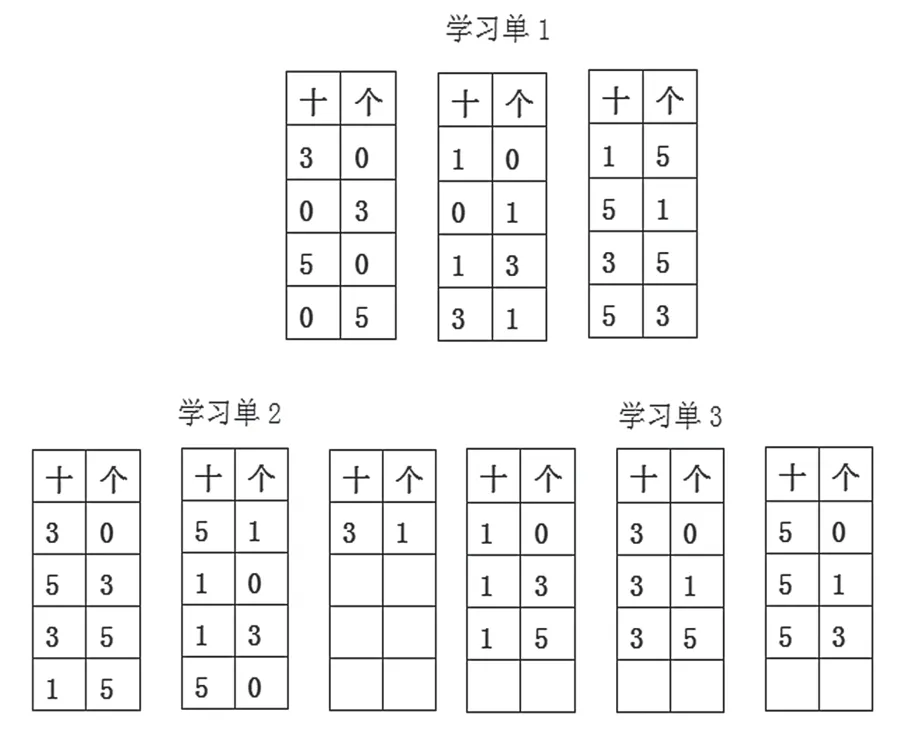
师：我在同学们的作品中找到了几个有代表性的，我们来看一看，请同学们观察下面的学习单，说说你有什么发现？

生：学习单1 是错误的排列，因为0 不能在十位。

生：学习单2 虽然出现的两位数都对，但是缺少顺序，容易遗漏。

生：学习单3 的排列有顺序，用固定十位的方法组成了9个两位数，有顺序、不重复、不遗漏。

师：刚才大家一直说在排列的过程中要有顺序不遗漏，具体应该怎么做呢？

生：先固定个位，然后依次进行排列。个位是0，然后十位就可以是 1、3、5，两位数就有 10、30、50；个位是 1，符合条件的两位数有31、51；个位是3，符合条件的两位数有13、53；个位是 5 ，符合条件的两位数是 15、35，共 9 个两位数。

生：先固定十位，然后依次进行排列。如十位上是1，个位可以是 0、3、5，两位数就有 10、13、15；十位是 3 ，符合条件的两位数有30、31、35；十位是5，符合条件的两位数有50、51、53，一共9 个两位数。这样出现的数字还能保证从小到大的排列。

师：看来为了使我们的思考更加有序，我们可以固定某一位，十位或个位，使另外的几个数字按照从小到大的顺序依次进行搭配，做到有序思考、不重复不遗漏，同时还要关注十位上不能出现0。（板书：有序思考 不重复不遗漏）

通过任务单提供学习性支架，引导学生在实践中发现排列的多种可能。通过学习单的展示，发现问题，引发学生更加关注有序思考的重要性。

活动二：观察对比找策略

师：用数字1、3、7、9能组成多少个没有重复数字的两位数？请你在学习单上写一写。

（学生独立尝试，教师搜集学情。）

汇报：他们的方法你看懂了吗？请你说一说。

展示不同学情，全班进行交流。

生：先固定个位，然后将剩下的数字放到十位上，依次进行排列。个位是1，然后十位就可以是3、7和9；个位是3，符合条件的两位数有 13、73、93；个位是 7，符合条件的两位数有17、37、97；个位是9，符合条件的两位数是19、39、79，共 12 个两位数。

生：先固定十位，然后将剩下的数字放到个位上，依次进行排列。十位是1，然后个位就可以是3、7和9；十位是3，符合条件的两位数有31、37、39；当十位是7的时候，找出的两位数有71、73和79；当十位数是9的时候，找出的两位数是 91、93、97，共 12个两位数。

追问：两种方法看似不同，但思考的本质是相同的。都是先固定一个数位上的数字，再按顺序排列另几个数。你更喜欢哪一种方法呢？请结合着你自己的理解适当修改完善你的学习单，然后把你排列的方法跟同桌说一说。（同桌再次交流方法。）

师：对比这两次活动，要求相同，为什么结果不同呢？

生：0 是一个特殊的数字，0 不能在十位出现，所以十位上只能是 1、3、5。所以用 0、1、3、5 只能组成 9 个没有重复数字的两位数。

师：确实0 的出现让我们看到了新的问题，在有0的排列中我们首先要思考0不能在十位，然后再用固定数位的方法依次进行搭配，做到有序思考、不重复、不遗漏。（板书：0不能在十位）

本环节教师借助有梯度的学习活动，引导学生的思维活动逐步走向深入，从而掌握有序、全面思考问题的方法。设计中的两个重要活动，都是用不同的数字组成两位数，然而在教学目的和层次上又是不同的。在活动一中，先让学生自主尝试解决例1的问题，在交流对比中发现问题，体会有序思考的必要性，进而探究有序思考的方法。在活动二中，引导学生运用所学策略，尝试有序思考解决问题，同时在两次活动的比较中，发现4个数字中有0的情况。通过活动二的再次对比，借助直观表格，呈现数字排列规律，运用数形结合思想，引导学生形成正向迁移提炼方法策略，促进思维发展。

（3）巩固练习，提升运用

基础练习 ：“做一做”第 1 题：用 0、3、5、7 可以组成多少个没有重复数字的两位数？

变式练习：“做一做”第2题：把5 块巧克力全部分给小丽、小明、小红，每人至少分一块，有几种分法？

拓展练习：用 1、3、5、8 组成没有重复的两位数，组成多少个个位是单数的两位数？

数学思想方法是数学的灵魂，它反映着数学知识的本质与核心价值。练习中教师精心设计有梯度的习题应用，关注基础知识和基本技能的理解与掌握。强化有0 的数字搭配，进一步巩固本节课的学习方法，引导学生在解决问题中反复感悟、体验领悟分类的数学思想。

从上面的教学中，我们不难发现要让学生掌握一种思想方法，就要先充分了解学情，找到学生最近发展区，挖掘教材把握教学契机，设计符合学情的活动。分类思想要逐类逐级讨论，适时为学生提供学习支架，帮学生建立新旧知识之间的联系，让学生体会到现在所学内容，就是在以往的知识和方法上又添了一些新情况而已，渗透分类思想。让学生在类比中发现和总结新的方法，逐渐完善知识的整体结构，体会分类思想在解决问题中的作用。