PI-DBN 在滚动轴承故障诊断中的研究
2022-11-01肖杨李亚王海瑞常梦容
肖杨,李亚,王海瑞,常梦容
(650500 云南省 昆明市 昆明理工大学 信息工程与自动化学院)
0 引言
滚动轴承作为一种十分重要的零部件,广泛应用于机械设备内部。当今滚动轴承的重要性越来越明显,其工作精度和可靠度对设备整体的运行状态都有关键性影响,使轴承故障诊断系统精度越来越高是故障诊断研究的主要方向[1]。
近年来,随着GPU 的快速发展及大数据时代的来临,深度信念网络(DBN)已席卷人工智能各个领域[2]。熊景鸣[3]等将深度信念网络与粒子群优化支持向量机相结合提高了故障诊断的准确率;沈长青[4]等提出一种基于Nesterov 动量法的独立自适应学习率优化的深度信念网络,引入Nesterov 动量法代替传统动量法预测参数下降的位置,控制参数达到最优点的速度,避免了传统动量法引起的错过最优点问题;杨宇[5]等提出结构自适应深度信念网络(SADBN),当诊断对象确定后,该网络可以排除人为因素的干扰,充分利用网络优势,自适应地选取最优深度网络结构,从而可以有效提高诊断精度及诊断效率,满足实时诊断的需求。
然而伴随着深度神经网络模型的性能增加,神经网络的深度越来越深,接踵而来的是深度网络模型[6]的高存储、高功耗以及深度学习模型效率低等问题,尤其是在低资源环境条件下,学习一个好的深度学习模型将产生规模巨大的网络参数,计算和存储成本也大大增加,最终导致花费巨大的时间代价。在神经网络中,过参数化训练被认为是神经网络必要一环,但Dong 等[7]指出,不是模型越深越复杂就能取得良好的分类性能,反而有可能出现过拟合、模型参数大多导致计算量大、脉冲强度消失等问题,因此过参数化训练并不显得特别重要。
本文提出一种PI-DBN 在滚动轴承故障诊断中的研究方法。首先选取一个过参数化的深度信念网络结构,在某些判别条件下,选取一些代表了整个模型的具有较高的训练价值的参数信息,而将剩余冗余的权值等信息进行删除,期望压缩后的模型能够达到原始过参数化训练时一样的效果;其次,将轴承故障数据输入到模型中,运用剪枝算法对冗余权值进行压缩;最后,分别用预定义目标网络架构和另外2 种剪枝算法进行对比性能分析。实验结果表明,保留下来重要权值信息在整个模型训练中能达到一个较好的分类效果,整个模型在迭代过程中能够较快地寻找到一个更加高效的模型结构。
1 基本原理
1.1 深度信念网络
深度信念网络(DBN)是由多层受限玻尔兹曼机(RBM)堆叠而成的神经网络模型[8],网络结构如图1 所示。
玻尔兹曼机有2 层神经元,一层为显层,将数据输入;一层为隐层,对数据进行特征检测[9]。显层和隐层之间通过权值互相连接,层内的神经元元间不存在连接。隐层单元被训练去捕捉在可视层表现出来的高阶数据的相关性。RBM 是一个随机网络,描述一个随机网络主要有2 点:(1)概率分布函数:联合概率密度、条件概率密度和边缘概率密度。(2)能量函数:随机神经网络的基础是统计力学,能量函数是描述整个状态的一种测度。系统越有序或者概率分布越集中,系统能量越小,反之,越无序并且概率分布越发散,则系统能量越小。
RBM 可见层和隐含层之间的能量函数为
式中:i ——可见层节点数;j ——隐含层节点数。由能量函数可以得出可见层和隐含层之间的联合概率密度为
通过联合概率密度可以得到可见层的独立分布为
此时得到一个含参数θ={w,b,c}的特殊Gibbs分布,根据联合概率,可以得出条件概率为
由于同层之间神经元没有联系,相互独立,当给定可见层神经元状态时,隐含层上某个神经元没激活的概率为
同理可得:
式中:sig——sigmoid 函数,sig(x)=1/(1+e-x)。
RBM 的训练目标是让Gibbs 分布最大可能地拟合输入数据,即让RBM 网络表示的Gibbs 分布与输入样本的分布尽可能地接近,可用样本分布和RBM 网络的边缘分布的KL 距离表示二者之间的差异性,KL 距离为
1.2 脉冲强度剪枝
脉冲强度(Spiking intensity,SI)是指一个神经元对输入其信号的反应程度,表征的是该神经元的活跃程度。如果一个神经元的SI 较大,说明这个神经元对输入信号具有较为活跃的反应;如果一个神经元的SI 较小,说明这个神经元对输入信号的反应较弱。SI 的表达式定义如下:
式中:α——一个正常数;Oi.l——第i 个隐含层中第i 个神经元的输出,i=1,2,3,…,Nl,且Nl是第l个隐含层的神经元个数。——第l 个隐含层中第i 个神经元的输入权值之和,如式(10)所示。
式中:rij——第i 个神经元的第j 个输入;wij——第i 个神经元与第j 个输入神经元之间的连接权值;ni——第i 个神经元的所有输入神经元个数。
1.3 PI-DBN 剪枝流程
基于PI-DBN 的具体剪枝流程(参见图2):
(1)对原始信号进行FFT 预处理,去除噪声等无效信息;(2)初始化深度信念网络参数;(3)对输入信号x 进行训练,使网络损失函数收敛;(4)对权值通道重要性进行排序。在每层中,计算权值通道的脉冲强度分数,并根据重要性分数按从小到大的方式对权值通道或进行排序。(5)依据设定阈值剪除一部分权值通道,达到模型压缩效果;(6)保留压缩后的神经网络结构,输入测试数据对模型进行故障分析和诊断。
2 实验
2.1 轴承故障数据说明
此次实验采用的是美国凯斯西储大学轴承数据中心采集的轴承故障数据集。数据集为12 kHz采样频率下的风扇端轴承数据,分别采集正常(OF)、内圈故障(IF)、滚动体故障(RF)以外圈故障(6 点钟方向)4 种不同状态的故障数据,除正常数据外每种状态有3 种故障深度类型,直径分别为0.177 8,0.355 6,0.533 4 mm,轴承电机载荷为0,轴承转速为1 797 r/min,总共10 种故障类别作为本次实验的数据来源。每类数据划分为115个分类样本,10 类总共1 150 个样本。训练集大小为700 份,即每类70 份,测试集为450 份,每类45 份。分类情况如表1 所示。
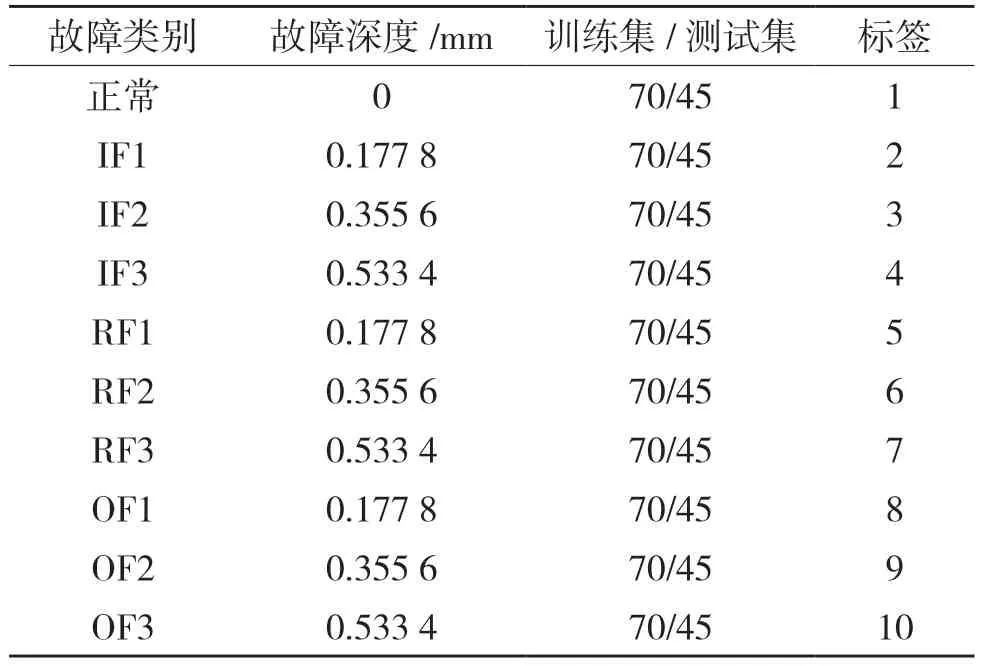
表1 轴承故障数据集描述Tab.1 Description of bearing failure dataset
2.2 实验结果分析
实验设置一个隐藏层,初始隐藏层含有10 个节点,设置DBN 预训练阶段的学习率为0.1,动量为0,微调阶段学习率为2,动量为0.5,并设置剪枝算法的剪枝率为50%。
分别对2 个不同网络架构进行实验,其中原始DBN 为未修剪过的深度信念网络,PI-DBN 为经过脉冲强度修剪过的深度信念网络。剪枝算法对神经元的活跃程度强度进行大小排序,并按照剪枝率对相应的权值通道进行归零,小端剪枝是将神经元较小的权值通道进行归零,随机剪枝则是不论大小随机归零50%的权值通道。不同窗口大小进行100次迭代后运行结果如表2 所示。
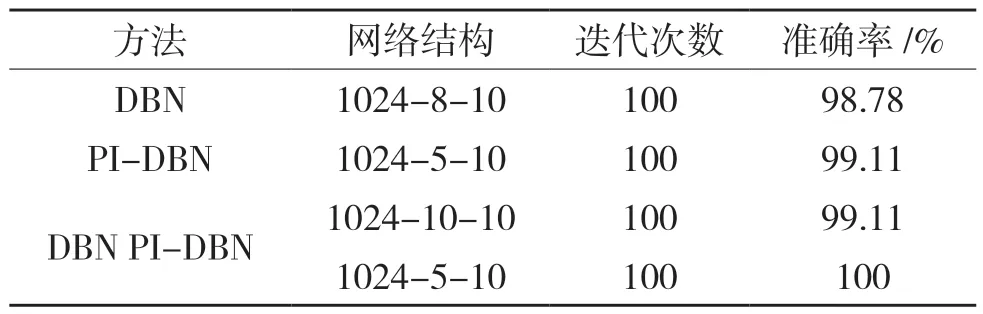
表2 方法准确率对比Tab.2 Comparison of method accuracy
从表2 结果可以看出,经过100 次迭代后,原始神经网络结构最高识别准确率为99.11%,最低为98.78%,而利用脉冲强度剪枝后进行学习分类的网络结构最高可达100%,最低也能达到99.11%,均高于原始DBN 网络架构。因此,相比原始DBN 网络,脉冲强度剪枝后的DBN 具有良好的分类性能。由此可说明在小规模权值通道下,脉冲强度剪枝保存的权值矩阵相比于预定义架构更能表征原始特征,权值的变化趋势对小型网络结构具有较强的分类能力。
为了体现数据维度关于脉冲强度权值剪枝的意义,将原始数据划分为1 024、512 两个不同窗口大小的数据集,利用脉冲强度剪枝对原始DBN进行修剪,迭代最大阈值为100,PI-DBN 为脉冲强度剪枝、DBN 为原始网络,并和基于权重剪枝以及随机剪枝结果进行对比,运行结果如下:
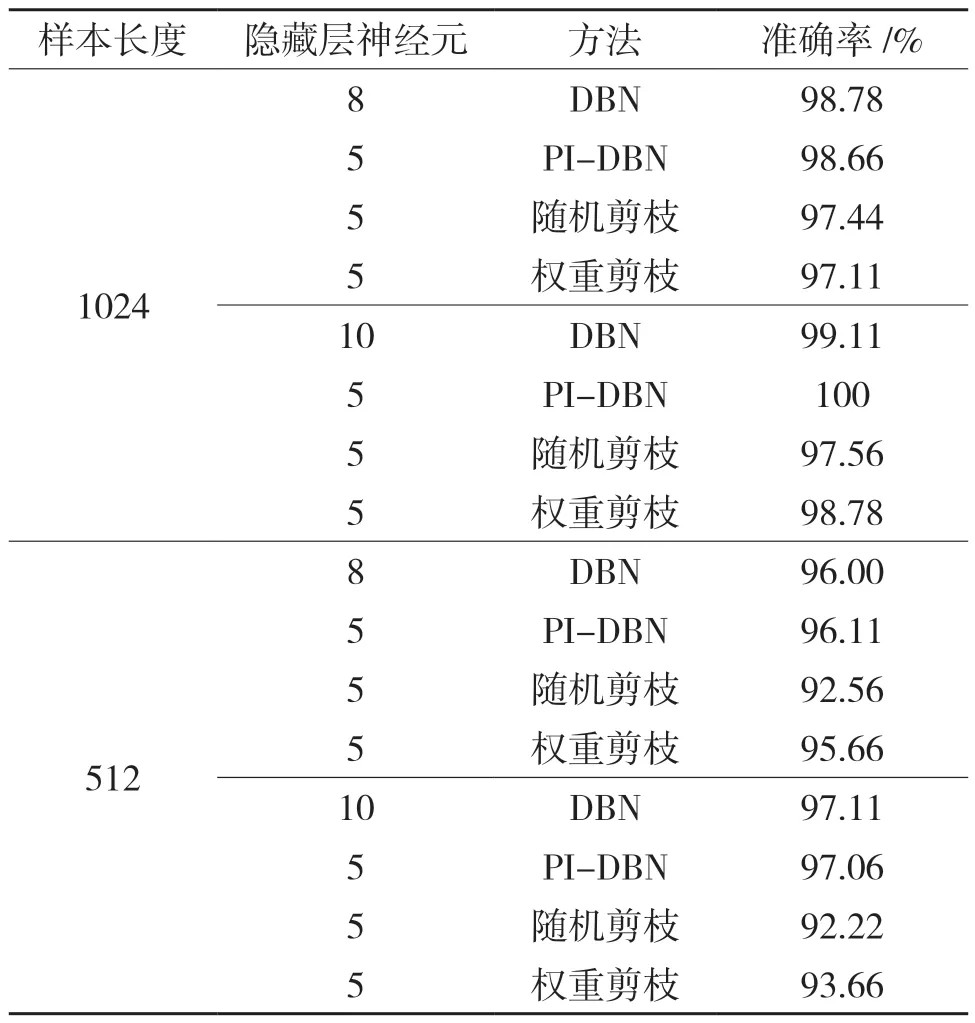
表3 不同模型以及维度准确率对比Tab.3 Comparison of accuracy of different models and dimensions
通过以上实验结果可以得出,脉冲强度剪枝算法对于低维数据集更加敏感,并且在更加小型的神经网络下,剪枝算法继承的权值信息具有较强的特征表现力,在不同维度下都取得较好的分类效果,最高可达100%的分类准确率。本次实验与其它两个剪枝算法相比,脉冲强度剪枝能够较好地保存原始数据的特征,较大概率剪除影响较小的神经元,并且脉冲强度剪枝后的模型精度均和原始网络并无多大变化,甚至可以比原始DBN 具有更好的分类性能。因此可以分析得到,当权重规模较小时,通过剪枝算法保存的网络结构将具有更强的分类性能权值变化大小能够较好地表现原始数据的特征信息。
为了更好地体现权值通道的重要程度,进行收敛性对比实验。设置迭代次数从0 开始,迭代100次为结束条件,记录每次实验的准确度,绘制收敛折线图,如图3 所示。通过收敛折线图进行PIDBN 的收敛性分析,其中RAND-DBN 为随机剪枝,DBN 为原始网络,W-DBN 为权重剪枝。从图3 可以看出,经过随机剪枝的方式去除一定的权值通道相比原始DBN 收敛性有较大的降低,原因是随机剪枝剪除的神经元重要性无法确定,在剪除时去除掉了重要性较高的权值通道,因而导致收敛性和准确性都有所降低。而通过脉冲强度剪枝确定的权值矩阵建立的模型则具有较大的合理性。通过判别方法辨别出重要性程度较高的权值通道,剪除影响性较低的通道,使得收敛性有一定的改善,并且在收敛的最后阶段时间内基于PI-DBN 的模型具有较强的鲁棒性。
图4 为不同维度下删除多个节点的准确率示意图,收集了当前维度下删除规定节点后所有可能的准确率数据。图4(a)、图4(b)为原始节点为8 个,然后进行脉冲强度剪枝,保留5 个节点。可以看到,原始数据为512 维度时最低准确率为0.88 左右,最高为0.97 左右;1 024 维度时最低准确率为0.88 左右,最高为0.99 左右。图4(c)、图4(d)为原始节点为10 个,然后进行脉冲强度剪枝,保留5 个节点。可以看到,原始数据为512维度时最低准确率为0.83 左右,最高为0.98 左右;1 024 维度时最低准确率为0.88 左右,最高为1.00。由图4 可知,脉冲强度在4 种情况下的准确率分别达到了96.11%、98.66%、97.06%、100%,均达到了删除相应节点后的较好水平,相较其他剪枝算法保持了较高准确率,达到了相应的实验目的。
3 结论
深度信念网络(DBN)在预训练阶段学习阶段以无监督逐层贪婪的方式获取数据的权重特征,权重变化在低维数据集下具有较强表现能力。本文通过脉冲强度剪枝删除权值冗余部分,压缩权值规模。对比不同维度剪枝后的收敛能力,得到如下结论:经过脉冲强度剪枝后权值信息在低维数据集下能够较好地表征数据的特征分布,使其快速收敛;随着数据维度的不断降低,脉冲强度剪枝收敛速度相比原始网络获取的收益更大;当权值矩阵规模较小时,变化较大的权值将具有较强的数据特征表现力。
因此在低维数据集下,建立小型神经网络,然后进行剪枝算法剔除冗余权值使模型快速收敛,具有较大的工程应用价值。
