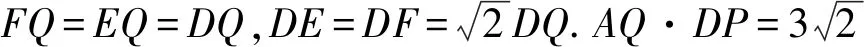抓住关键特征，破解中考压轴题——一道与正方形有关中考压轴题的多角度求解

张斌武

(甘肃省天水市育生中学，甘肃天水，741000)

1 试题呈现

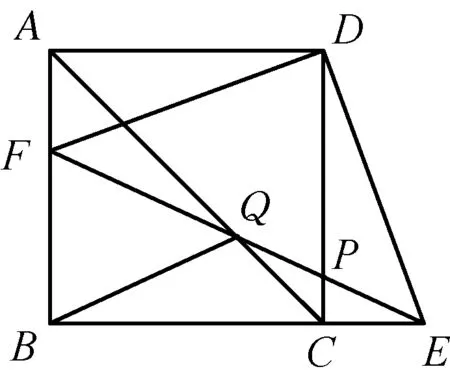
图1

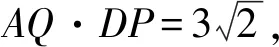
2 问题分析

图2

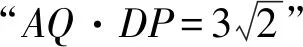
由平行线的性质，易知∠FGC=∠ACE，∠GFE=∠CEF.

由正方形的性质，易知AF=FG.

由旋转的性质，易知AF=CE，所以FG=CE.

从而可知△FGQ≌△ECQ，所以FQ=EQ，即点Q是线段EF的中点.

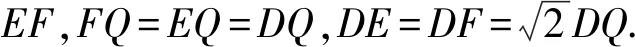
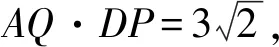
3 解法探究

基于以上分析，笔者从不同角度出发，给出本题的多种解法.

视角1利用特殊化策略求解

根据已知条件，点E是边BC的延长线上的动点，点F是边AB上的动点，且AF=CE.不论点E，F运动到什么位置，点Q恒是线段EF的中点，它是运动不变量.因此，对于一道填空题而言，可考虑利用特殊位置法求解.

图3

解法1如图3，当点F与点A重合时，点E与点C重合，点P与点C重合，即线段EF与正方形ABCD的对角线AC重合，线段DP与正方形ABCD的边DC重合，此时点Q是对角线AC的中点.

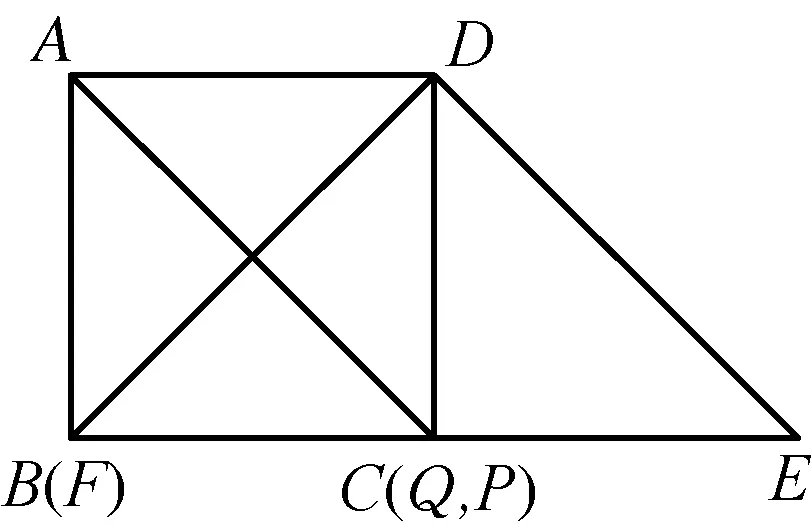
图4

解法2如图4，当点F与点B重合时，点Q和点P均与点C重合，线段AQ与正方形ABCD的对角线AC重合，线段DP与正方形ABCD的边DC重合，此时点Q是线段EF的中点.

点评当几何问题中的已知条件和所求量之间的逻辑关系不明显时，可考虑动点或动线段的特殊位置，这是解决几何问题的一种特殊化策略，具有化难为易，化繁为简之效果，可快速得出问题的答案，是解决选此类择题或填空题的一种“秒杀”法.构造特殊图形时，要注意保证运动不变量恒成立.

视角2利用相似三角形的性质求解

利用相似三角形的性质将AQ·DP转化为与线段DQ有关的另两条线段之积，然后通过列方程求解.

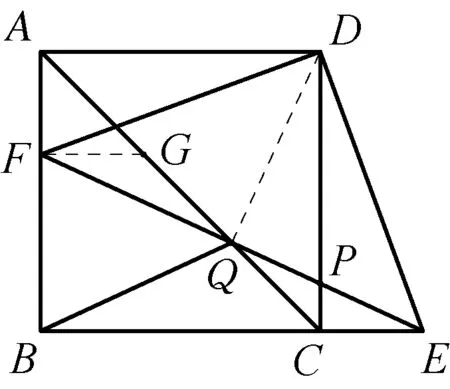
图5

解法3如图5，连接DQ，过点F作FG∥BE，交AC于点G.

易知△DEF是等腰直角三角形，所以∠DFE=45°.

由正方形的性质，易知∠DAC=45°，所以∠DFE=∠DAC.

又因为∠AGD=∠QGF，所以∠ADF=∠AQF.

易知△ADF≌△CDE，所以∠ADF=∠CDE.

从而可知∠AQF=∠CDE.

又易知∠AFQ=∠DPE，所以△AFQ∽△EPD.

所以AQ·DP=FQ·DE.

易知△FGQ≌△ECQ，所以FQ=EQ.

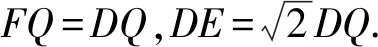
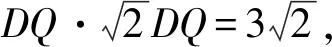
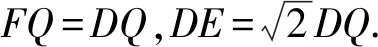
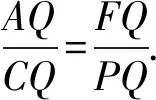
①

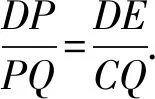
②

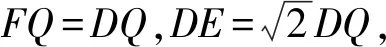
视角3利用“设而不求”解题法求解

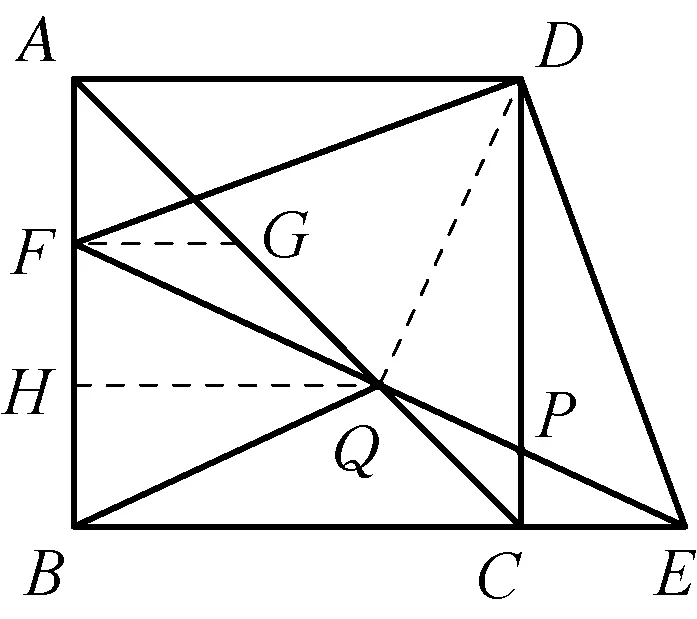
图6

解法5如图6，连接DQ，过点F作FG∥BE，交AC于点G.过点Q作QH⊥AB，垂足为H.

设正方形ABCD的边长为m，AF=x，则CE=x.

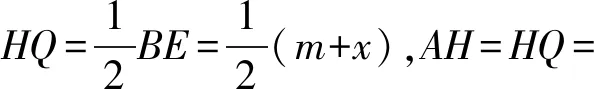
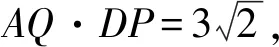
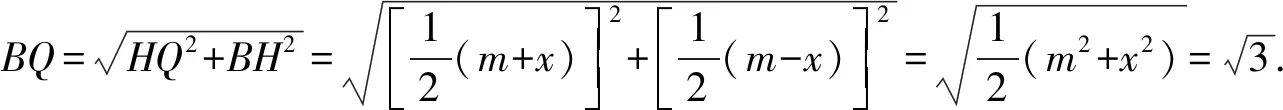
点评在数学问题中，如果已知量较少，可考虑利用“设而不求”解题法求解.在解决数学问题时，预先设定一些未知数，把它们当成已知数，然后根据数学问题中各量之间的逻辑关系列出方程，求得未知数.或预先设定一些不需要求出未知数，然后根据数学问题中各量之间的逻辑关系，将未知数消去或代换.“设而不求”解题法能够起到化繁为简，化难为易的作用.

视角4利用解析法求解

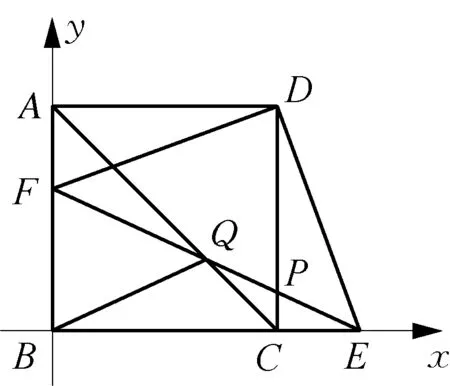
图7

解法6以直线BC为x轴，以直线AB为y轴，建立平面直角坐标系.

设A(0，m)，F(0，n)，则C(m，0)，E(2m-n，0).

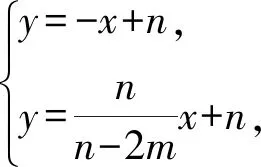
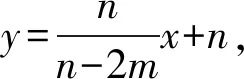
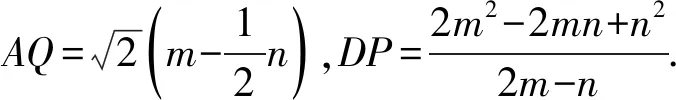
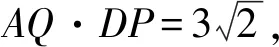
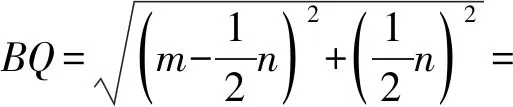
点评解析法是解决与直角三角形、等腰三角形、正方形等几何图形有关的几何计算问题的一种重要方法.利用解析法解决平面几何问题，一是要根据图形特征建立适当的平面直角坐标系，将有关线段的长度转化为某些关键点的坐标；二是要将几何问题转化为代数问题，通过求某些直线的表达式或某些点的坐标解决问题.通过利用解析法解决平面几何问题，突破了学生解决平面几何问题的思维定势，促使学生重新审视已有的平面几何问题的求解方法与思路，有利用培养学生的创新思维和创新意识，从而提升学生的数学创新素养.

4 结束语