磁轴承转子跌落在保护轴承上的动力学研究

汪军水 贾翔宇 张 剀 徐 旸

清华大学工程物理系，北京，100084

0 引言

随着国民经济水平的提升和社会的快速发展，旋转机械在国家工业建设中扮演的角色愈发重要，在国防、军工、化工、航空、航天、交通、能源等领域都得到了广泛的应用。旋转机械的安全、稳定运行离不开轴承的可靠支承。主动式磁轴承是一种新型轴承，其表面不与转子产生接触，具有清洁、无磨损、能耗低、寿命长等一系列优点[1]，拥有其他传统机械轴承难以比拟的优势。

磁轴承能够得到广泛应用，离不开上文中提到的优势，但由于动力学失稳、轴承过载以及电子学系统部分故障等因素，转子可能出现较大的动态位移，此时主动式磁轴承将失去对转子振动的有效控制[2]。因此，需要一个具有更强承载能力的保护轴承来提供附加承载，以避免磁轴承失去支承作用时转子直接跌落对系统造成的破坏。

事实上，保护轴承的承载也是有限的。在磁轴承突然失效的机器中，转子的碰撞、冲击、弹跳将对保护轴承产生剧烈冲击，对磁轴承设备造成巨大破坏。国内外磁轴承设备由于保护轴承没有起到保护作用而损毁的事故时有发生。文献[3]中，由于保护轴承没能发挥作用，轴颈、备用轴承和密封件出现了严重损坏。文献[4]中，出现了因转子过载失控跌落在保护轴承上而导致其损坏的事故。因此，研究转子跌落在保护轴承上的动力学行为非常必要。

转子跌落在保护轴承上的响应是一类复杂的非线性动力学问题，国内外学者对此问题已经做了一系列研究。从系统结构建模来看：经过30多年的研究，保护轴承-转子系统的建模得到了不断深化，转子模型由最初的单平面转子模型发展到如今多节点的有限元模型[5-7]；轴承模型从质量-弹簧-阻尼模型发展到现在能深入刻画球轴承内部单个滚珠响应行为的复杂力学模型[6-8]。从局部接触模型来看：径向接触模型从最早的胡克模型研究发展为目前常用的非线性赫兹接触模型[9-11]；切向摩擦力模型在库仑摩擦的基础上发展出组合摩擦模型，有研究者也根据高速滑动特性推导出摩擦因数量化公式[12-14]。从研究方法来看：大部分文献运用数值模拟的方法，从理论上揭示了转子跌落过程中出现的诸多非线性行为，如反向涡动、前向涡动[15]、瞬态非线性灾变振动[8]、恒频涡动[16]等；部分研究者搭建了跌落试验台，开展了高速转子跌落响应实验，观察到了转子在保护轴承上丰富的动力学响应现象，验证了在数值模拟中出现的部分的非线性行为[5，17-20]。未来此课题的研究将进一步完善系统结构模型和接触模型，从理论上对动力学行为进行研究，同时将研究保护轴承新结构以提升系统安全性，并开展相关实验。

如上文所述，转子跌落在保护轴承上是一个非常复杂的多因素问题，任何参数和模型的变化都可能对研究结果产生较大影响，不同研究得到的跌落响应结论往往存在一定的局限性。目前，针对此问题国内外的研究结论很多，但尚未见系统梳理跌落过程研究的综述性文章。

本文主要关注磁轴承转子跌落在保护轴承上的动力学研究，特别是理论研究，对近30年来该问题的代表性成果进行了整理，以期对后续研究起到指导作用。首先，对转子跌落研究中涉及的两个主要接触力模型——径向接触力模型和切向摩擦力模型的发展进行综述；接着，对保护轴承-转子系统动力学模型的发展进行综述；然后，从转子响应形态与系统结构参数之间的关系切入，对目前研究中得到的结论进行了总结归纳；进一步地，根据调研得到的研究成果，总结了保护轴承-转子系统设计优化的部分通用准则；最后，总结归纳得到了本文的结论，并从模型建立、计算方法和工程中轴承结构与参数优化等三个方面，给出了转子跌落在保护轴承上这一问题的研究发展方向。

1 局部接触模型

转子与保护轴承相互接触是一个典型的非线性问题。高速转子跌落时的相互作用往往是瞬时大冲击，且接触条件相对复杂，目前没有物理模型能够完全准确描述这一力学过程。为了相对准确地刻画转子与保护轴承在局部发生相互作用的力学过程，根据研究的主要目标如轨迹模拟、作用力估计、形变和位移计算等，研究者可以选用不同的局部接触模型。从接触变形来看，局部接触模型主要分为刚性碰撞模型和弹性碰撞模型两类。刚性碰撞模型在早期的定转子碰摩研究中应用较多，主要针对转子与保护轴承之间的全周涡动这一运动形式进行研究，定性分析了阻尼、摩擦、模态等因素对简化模型涡动的影响[21-23]，由于其只定性研究，本文不做深入介绍。近年来，在转子跌落的非线性动力学研究中，主要使用弹性碰撞模型，这种模型能够准确反映转子与保护轴承接触过程中的运动轨迹、作用力、位移等细节变化。其中，基于恢复系数的弹性碰撞模型在早期研究中的应用居多，基于有限变形理论的弹性碰撞模型是目前研究中使用的主流方法。

1.1 基于恢复系数的接触模型

基于恢复系数的接触模型是最简单的弹性碰撞模型，此模型推导得到了转子跌落碰撞前后的速度关系[5，24]。MUSZYNSKA[5]首先引入了切向和法向速度恢复系数，其中，法向速度恢复系数是碰撞前后法向速度的比值，切向恢复系数用来表征切向的速度变换关系。在接触过程中，转子与保护轴承每发生一次碰撞，转子的一部分速度就会转移到保护轴承内圈中，因而切向速度恢复系数是一个递减值，这种递减规律可以用一个速度递减系数来表示。另外，切向速度恢复系数还可以用作考虑保护轴承的旋转自由度。两个速度恢复系数的表达式如下：

(1)

基于恢复系数的碰撞模型中，保护轴承是固定的。采用恢复系数时，转子与保护轴承在接触点的物理参数没有直接反映出来，不利于刻画实际转子-保护轴承系统参数对碰摩响应行为的影响规律。该模型更适用于定性研究跌落响应系统可能出现的动力学现象，因此，后续的跌落研究都不再基于此碰撞模型进行深入分析。

1.2 基于有限变形理论的接触模型

基于有限变形理论的碰撞模型能通过建立合适的径向接触力和切向摩擦力模型，将转子与保护轴承相互作用时的复杂动力学过程模型化，并能通过非线性求解工具数值求解。该碰撞模型的优势在于：一方面，能够有效刻画转子与保护轴承之间弹性碰撞的轨迹；另一方面，能够通过径向接触力模型和切向摩擦力模型量化接触过程中作用力和位移等参数的大小。

1.2.1径向接触力模型

在保护轴承与转子的相互作用过程中，会产生一定的挤压变形，胡克定律是描述接触力与变形之间关系的最经典模型，表达式如下[9]：

F=kδ

(2)

式中，k为刚度系数；δ为碰撞体的挤压变形量；F为法向接触力。

k可以通过有限元方法获得，也可以通过在线弹性域内进行的实验测试来确定[25]。WANG等[26]、张楠等[27]运用胡克模型进行了转子碰撞问题的仿真研究。

纯粹的弹性碰撞模型无法表达碰撞过程中的能量耗散问题，KELVIN等提出了耗散接触力模型，以适应内部阻尼的能量耗散问题[10]：

(3)

式中，c为黏滞阻尼系数，取决于接触涉及的材料和尺寸等参数。

此模型引入了碰撞时的能量耗散特性，能够表达出碰撞过程中的弹性过程和能量损耗过程且形式简洁，是转子跌落仿真研究中一种常见的模型[6，28-31]。

在接触的线性耗散力模型之外，结合赫兹理论引入的非线性接触力模型-赫兹接触模型[11，32]，得到进一步改进的碰撞力表达式为[33]

(4)

式中，χ为黏滞阻尼因子；m、n为与物体间的材料和接触状态有关的参数。

此模型能够表达转子与保护轴承间的非线性接触力，在转子跌落仿真领域被广泛应用[4，7，34-36]，但缺点在于k、δ、m、n等的取值难以确定，且直接物理意义尚不清晰。

一般认为，只要采用合适的刚度系数和黏滞阻尼系数，采用不同的径向力模型对转子与保护轴承相互作用的定性研究结果影响不大[37]，但在定量研究过程中不同模型以及模型的参数选取得到的计算结果可能产生较大差别。此时，结合实际工况进行模型及参数选取，将决定仿真模拟的准确性。

1.2.2切向摩擦力模型

摩擦力是保护轴承与转子相互作用的主要作用力之一，转子在保护轴承上的后向涡动主要由摩擦力驱动。目前最常用的切向摩擦力模型为库仑摩擦模型[12]：

Fμ=μNsgn(vrel)

(5)

式中，N为法向接触力；vrel为转子和保护轴承接触点的相对速度；μ为摩擦因数。

在库仑摩擦模型的基础之上，考虑转子和保护轴承相对静止时存在的静摩擦力，最大静摩擦力通常大于滑动摩擦。方之楚[8]、祝长生[38]在静摩擦时通过求解静力学方程获得了静摩擦力数值，但数值求解中，由于此方法无法严格判断相对静止而失去作用。为将产生静摩擦处的摩擦力模型进一步细化，更精确地描绘转子跌落在保护轴承上的摩擦作用过程，KARKKAINE等[13]使用了一种库仑摩擦模型、Stribeck摩擦模型[12，39]和静摩擦模型的组合模型：

μ=μc+(μs-μc)e-(vrel/vs)2

(6)

式中，μc为动摩擦因数；μs为最大静摩擦因数；vrel为相对运动速度；vs为Stribeck速度。

两种切向摩擦力模型如图1所示。

图1 两种切向摩擦力模型Fig.1 Two tangential friction models

在考虑转子与轴承之间发生高速相对运动时的摩擦力时，随着相对速度的增大，转子与保护轴承间出现的碰撞磨损将导致接触面的条件发生变化；同时，摩擦产生的热量由转子和保护轴承承担散热，构件温度及环境温度的变化将导致摩擦因数不为常数，此时摩擦因数越来越小[40-42]。ETTLES等[41]、BLOK[43]提出，对大多数材料而言，在严重滑动条件下摩擦因数可以被量化，并根据Blok理论给出了摩擦因数的量化公式。JIANG[14]在ETTLES等[41]的基础之上利用摩擦界面上摩擦力做功和热量的能量守恒关系，导出精度更高的高速滑动时的摩擦因数公式：

(7)

(8)

式中各参数的物理含义可参考文献[14]，以碰撞接触的两个碰撞体为核心，能够得到以上两个摩擦因数公式。N1、N2分别是粗糙碰撞体达到对应热分解温度所需的时间，该数值决定了式(6)的取用。

在研究中，变摩擦因数模型的表达式普遍比较复杂，且尚未有统一的模型。纵观转子跌落在保护轴承上的动力学研究，定量仿真分析时的主流摩擦力模型仍为库仑摩擦及其组合摩擦模型，变摩擦因数模型在研究中目前一般只用于定性分析。

2 转子-保护轴承系统结构模型

在磁轴承转子跌落研究中，系统结构主体为转子和保护轴承两部分，不同研究者分析问题时建立的转子-保护轴承的结构模型的侧重点有所区别。建立转子结构模型需要考虑转子单盘还是多盘、对称还是非对称以及考虑陀螺效应与否、离散与连续等诸多因素；建立保护轴承结构模型时需考虑自由度数量、含阻尼与否、限位方式、是否关注内部结构受力等方面。

2.1 转子结构模型

较简洁的转子模型为MUSZYNSKA[5]提出的单盘模型，将转子简化为二维刚体圆盘，不考虑其形变。在碰撞接触的相互作用描述中，引入径向恢复系数和切向恢复系数公式，能够定性研究转子跌落后的运动轨迹，并获得部分运动特性。但由于基于恢复系数的动力学过程无法反映相互作用中的细节，此模型的缺点是无法通过仿真模拟定量计算转子与保护轴承相互作用时的作用力及变形量等参数。

1992年，ISHII等[6]首次基于Jeffcott单盘转子模型对磁轴承失灵后的瞬态响应过程进行分析，建立了磁轴承跌落前后的动力学模型，并进行了计算分析。ISHII等[6]的模型将转子进行分段处理，各轴段之间引入了弹簧阻尼单元；同时，考虑模型具有高度对称性，最终简化为多自由度质量-弹簧-阻尼模型(图2)。2016年，CAO等[7]同样将转子分段处理，引入弹簧阻尼建立了跌落前后的动力学模型(图3)。两种模型都以分段模块化为基础，引入径向赫兹接触作用力模型以及库仑摩擦模型分别刻画轴承与转子接触的径向力与切向力；同时，多自由度能够更全面地反映转子各主要部件的瞬态动力学响应特性。但此模型的缺点在于，各轴段之间的弹簧阻尼连接模型过于简略，无法反映转子本身的结构特性及动力学响应特性；同时，连接刚度、阻尼等参数都难以通过理论或实验手段准确确定。

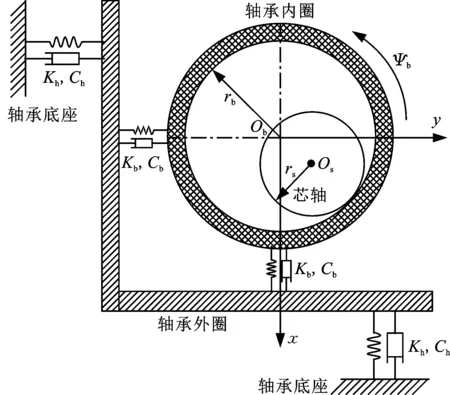
图2 文献[6]的跌落动力学模型Fig.2 Drop dynamics model of the reference [6]

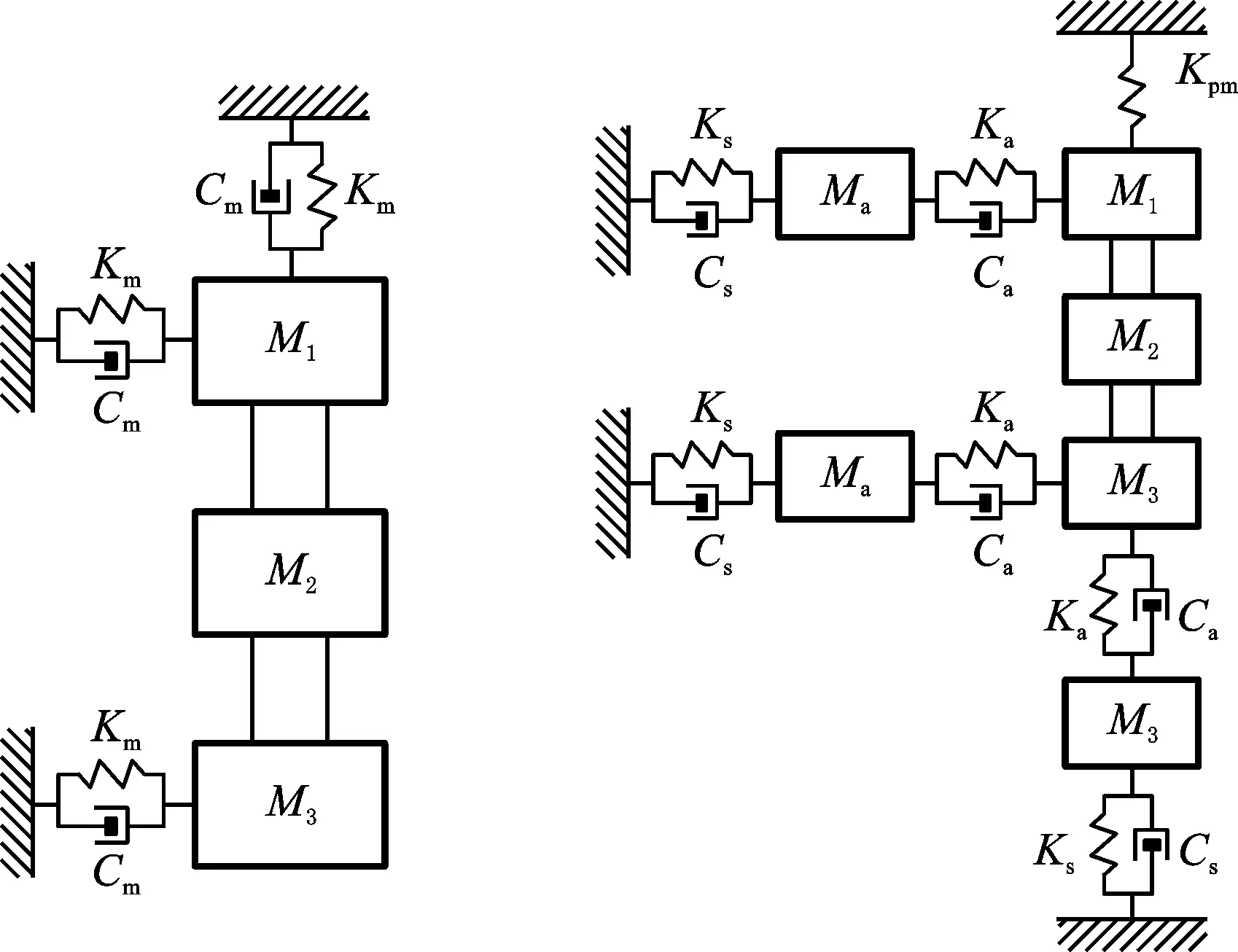
(a)跌落前 (b)跌落后图3 文献[7]的跌落动力学模型Fig.3 Drop dynamics model of the reference [7]

祝长生[38]基于有限元法，将磁轴承转子进一步扩展多段处理(图4)，得到了含陀螺效应的转子系统振动方程：

(9)

式中，UR为转子系统的广义坐标向量；M、C、G及K分别为转子系统的质量、阻尼、陀螺及刚度矩阵；FR，U和FR，amb分别为转子系统的不平衡力向量以及主动磁轴承(AMB)对转子的电磁力向量；n为转子的稳态工作转速。

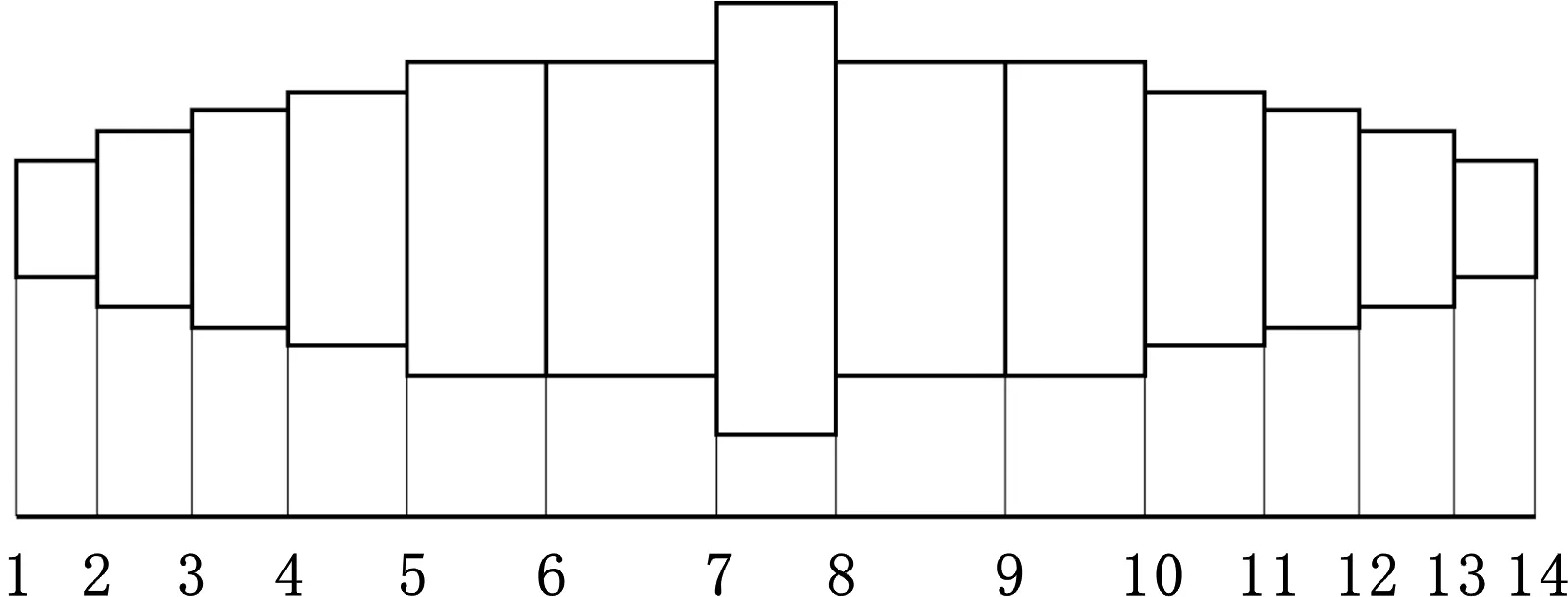
图4 转子有限元模型Fig.4 Finite element model of rotor

为了考虑转子单元的剪切变形，KARKKAINE等[13]采用Timoshenko梁单元对转子进行了有限元建模，由于对转子的分析主要集中在横向振动上，因此，该模型冻结了梁单元的轴向自由度和扭转自由度。目前，除研究者通过有限元法离散建立转子动力学模型之外，已经有非常多成熟的有限元商业软件如MADYN、ANSYS等，能够通过导入3D模型的方式建立转子模型，提高建模效率的同时能够将网格划分得更为精细。与研究者自行建立动力学方程相比，有限元软件对转子系统的建模能处理更为复杂的转子结构，同时获得更加准确的结果，并对转子的振动特性及跌落响应特性进行更为准确的分析。

2.2 保护轴承动力学模型

保护轴承可以分为三种类型，分别是衬套式、滚动元件式以及两者的复合。衬套式保护轴承结构简单、价格低廉、容易维修，但由于轴套磨损，保护轴承在转子减速时的摩擦特性会发生变化，磨损引起的高摩擦会使保护轴承耗散能量的能力下降，可能导致转子失稳。基于滚动元件轴承的保护轴承具有更为复杂的机械结构，对冲击也更加敏感。在摩擦力的作用下，保护轴承内圈会迅速达到与转子一致的角速度，滚动元件轴承能够降低转子与轴承的相互作用，一定程度上可以防止转子后向涡动的发生[39]。第三种保护轴承是上述两种轴承的组合，这种类型的轴承有一些缺点，如转动部件的转动惯量较大，与传统的滚动元件式保护轴承相比，这将使轴承角速度与转子角速度较晚达到同步。

为刻画转子在保护轴承上的运动，文献[6，8，44-45]建立了含支承阻尼和刚度的保护轴承模型。轴承具有平面内平动和绕Z轴转动三个自由度，轴承的内部结构不作细致考虑，只考虑轴承与轴承座及转子之间的相互作用。SCHMIED[28]对球轴承的建模与上文类似，与之不同的是在轴承变形处加以限定，使得在相互作用过程中将出现两种轴承与转子之间的作用力方程。

保护轴承大多为球轴承。进一步考虑轴承内部的运动情况，SOPANEN等[46-47]基于非线性赫兹接触变形理论和弹性流体动力膜理论提出六自由度深沟球轴承的动力学模型，KARKKAINE等[13]将其引入转子跌落仿真并证实了模型的有效性。CAO等[7，48]同样详细建模了球轴承内部结构，并采用迭代法和直接法进行了理论模拟，证明两种方法都有相似的响应结果，同时实验证实建立的球轴承模型可用于实际分析。WILKES等[16]也提出了一种新的保护轴承系统建模方法。

除传统滚珠形式的保护轴承之外，研究人员还研制了一系列新型保护轴承。CHEN等[49]研制的零间隙保护轴承在转速10 000 r/min的情况下经受了考验，降低了激烈摩擦导致后旋的可能性；2006年研制了用于飞轮装置的混合动力备用轴承，成功进行了多次转速为36 000 r/min的无辅助降落[50]；南京航空航天大学的相关学者研究了双层球保护轴承并引入了弹性环、公差环等结构，通过仿真模拟和一系列实验，证明了设计的可行性和一定的优越性[34-35，51-52]；吴浩[53]设计研制了间隙自消除保护轴承，并进行了一系列理论和实验，从热力学角度分析了该设计的可行性。

3 转子跌落瞬态响应结论

3.1 跌落响应形态

磁轴承通常应用于高速旋转机械，而高速转子携带有较大的转动动能，一系列研究表明，转子与保护轴承接触后会产生复杂的非线性动力学行为，并导致出现多种响应结果[54-57]。MASLEN等[15]将其总结为三种典型运动状态和一种混合运动形式(图5)，其中后向涡动是各类运动形式中最为剧烈的一种[58]，也是系统被破坏的主要因素。本文重点描述后向涡动。

图5 典型跌落运动形式Fig.5 Typical pattern of drop motion

MUSZYNSKA等[59]认为，摩擦力是产生涡动的重要因素。关于摩擦力导致转子后向涡动早在1934年就已经有所研究[60]。1968年，BLACK[61]考虑了干摩擦后旋相互作用，并与理论结构进行了定性比较。在切向摩擦力的作用下，转子的转动动能部分转化为转子的圆周运动能量，并在轴承的反作用力作用下高速绕轴承内圈涡动。后向涡动是一种破坏性较强的转子跌落响应形式，能够从三方面对转子和保护系统造成破坏[62]：首先，后向涡动产生的位置通常是环形密封位置，这里是间隙最窄的地方，转子和定子之间的接触力会严重损坏这些密封元件；其次，由于较大的旋转频率和离心力，转子可以达到较大的位移，这可能会造成转子的永久变形；最后，对保护轴承完整性最严重的威胁是摩擦扭矩，巨大的作用力矩可能会损坏剪切轴。JIANG[63]对发生反向全周涡动的机制和过程进行了较详细的论述，并强调在数值模拟时必须考虑干摩擦效应才能正确地模拟反向全周涡动的响应形式。

从振动特性来看，转子在保护轴承上的涡动来源于转子减速通过临界点时引起的强烈非稳态、非线性弯曲受迫振动，以及接触点的非线性特性[44]。转子的反向全周涡动与系统一阶固有频率有关[6，64]，当转子跌落转速小于系统一阶固有频率时，将产生同步涡动；当转子转速大于一阶固有频率时，将在固有频率处发生恒频全周涡动。进一步认为，当转子转速远高于一阶频率时可能在其他阶固有频率处产生恒频涡动[16]。

3.2 响应结果与系统结构关系

3.2.1转子结构

系统结构的影响主要包括转子和保护轴承两个方面。转子方面，由动力学仿真模型和实验模型可知，对于一个不完全平衡的磁轴承系统转子，转子的不平衡量与跌落后的响应结果有关。不平衡量越大，转子在备用轴承上响应的作用力和产生全周涡动的可能性越大[65]。转子的跌落位置与跌落时的初始状态以及跌落后的轨道和作用力大小有关，且这种影响随转子不平衡量的增大而增大[38]。同样，转子的转速越大，转子具有越高的转动动能，跌落时对备用轴承施加的作用力越大，越容易引起全周涡动。

3.2.2保护轴承参数

保护轴承方面，选用柔性支承的保护轴承有利于减小转子跌落时对转子和轴承的作用力[66]，WANG等[26]的研究也表明，增加保护轴承阻尼有助于降低旋转幅值，消除混沌响应，KUNCORO等[66]等也认为采用刚度支承和阻尼支承能够有效减小径向接触力。理论计算和仿真都表明，存在一种最优支承阻尼，使得转子跌落后出现全周涡动的可能性和转子与备用轴承之间的作用力都尽可能低[67]。祝长生[38]认为，不存在对所有转速都有效的最优阻尼区间；同时，研究结果表明，最优阻尼区间的最大值往往大于实际能达到的阻尼，因此对工程应用应尽可能大地增加备用轴承阻尼，将转子动能进一步耗散，以降低产生全周涡动的时间和概率。类似地，研究表明，采用带有波纹带阻尼的备用轴承能使得转子形成的全周涡动快速停止[28]。

摩擦力模型方面，不同摩擦力模型对转子跌落轨迹结果影响不大，但摩擦因数对跌落响应结果影响较大[37]。诸多研究表明，摩擦力将导致大响应和后旋的出现，特别是在小阻尼情况下，大的摩擦因数会将转子的自转动能更快地转换为涡动动能，且无法有效耗散，响应结果将对转子-备用轴承系统更加不利。

EBRAHIMI等[68]通过多种评价工具分析了保护轴承刚度对系统动力学行为的影响，说明了二者之间的显著关联。WANG等[26]指出，轴承刚度越大，转子下降后的全间隙向后转速和旋转幅值越高。ZENG[69]指出，适当的软支承刚度可以减少非线性共振，但如果轴的刚度过小，保护轴承将无法为转子提供有效支承。他们提出，在保护轴承设计中，轴承支承刚度可选择接近轴的刚度。INAYAT-HUSSAIN[70]研究认为，在抑制转子响应中的次同步和非同步振动成分方面，调整轴承接触刚度比调整库仑摩擦因数更有效。同时，MA等[71]通过分析认为，可以确定刚度的合理范围使转子运转于相对稳定的周期运动模式。也有研究表明，足够低的内环惯性矩可以降低转子出现后向涡动的可能性[28]。

FUMAGALLI[72]认为转子和保护轴承之间的间隙应较大，并指出，如果间隙足够大，转子就会像钟摆一样摆动，而不是旋转运动。但值得注意的是，当转子出现旋转运动之后，间隙越小，出现的径向作用力会越小。另外，转子和保护轴承之间的间隙通常约为AMB间隙的一半；由于AMB的磁力与间隙的平方成反比，间隙变化会导致磁轴承控制灵敏度改变，因此，转子和保护轴承之间的间隙不能仅考虑单一设计因素。

3.2.3保护轴承新型结构

保护轴承的新型结构研制也取得了突破。零间隙保护轴承已经在冲击和AMB故障条件下进行了实验测试，转速达到了10，000 r/min。试验结果表明，零间隙轴承不仅限制了转子的瞬态位移以保护磁悬浮轴承，而且在转子啮合后，还使得转子运动到离原轴承中心很近的位置。间隙的消除和阻尼特性减少了产生剧烈摩擦旋转的可能性[49]。双层滚珠备用轴承及其公差环弹性环等结构的设计，有效降低了转子跌落时对系统的冲击作用以及振动幅度，同时将系统摩擦的热量传递大幅降低，有效延长了系统的使用寿命[51-52]。基于刚性转子理论设计的间隙自消除备用轴承通过保护间隙的消除能有效减低碰撞力和涡动的可能[53]。YU等[73]设计了一种径向和轴向一体化的辅助轴承(RAIAB)，能消除转子跌落时的径向和轴向间隙，实现对转子的稳定支承。LIU等[74]提出了新型滚动-滑动一体化保护轴承，对转子跌落后的径向和轴向提供支承，并通过实验验证了新型轴承在最大冲击力和大冲击次数两个方面都比传统保护轴承小得多。GINZINGER等[75]、CADE等[76]考虑了变式保护轴承的可能性并进行了尝试；KEOGH等[77]研究的保护轴承驱动系统在理论上证明了通过主动调节保护轴承参数使转子重新恢复悬浮的可能性；还有相关学者利用压电驱动系统各自设计了主动保护轴承并实现了控制[67-77]。

4 保护轴承系统优化策略

转子失控跌落对转子和保护轴承都可能产生灾难性的打击，对其跌落过程中进行动力学研究的主要目的就是最大限度地降低相互作用带来的损伤。从转子跌落在保护轴承上的一系列研究结果来看，在进行AMB系统保护轴承设计优化时，尽管无法准确预测碰撞结果的所有信息，但针对部分已经明确的物理现象，可以参考一些具有先行性的指导：

(1)在转子运行前，可进行充分的动平衡以降低转子自身的不平衡量，降低因转子不平衡带来的系统振动[38，65]。

(2)摩擦因数越小，跌落响应中的作用力就越小，因此，应充分润滑以降低转子与保护轴承表面的摩擦因数，同时也能避免机械摩擦带来的损伤[37，8]。

(3)保护轴承的柔性支承结构至关重要，支承阻尼系数存在最优区间，但工程实践中阻尼系数难以达到最优区间的上限，通常可以认为阻尼系数越大越好[38，67]。

(4)跌落时衬套表面应采用高强度、低摩擦和高硬度的材料，以避免转子和保护轴承接触产生早期磨损[15]。

(5)保护轴承的支承刚度对跌落响应结果影响也很大，软支承刚度能降低非线性共振，但支承刚度过小无法为转子提供有效支承，因此通常采用与轴支承刚度接近即可[67，69-70]。

(6)从跌落响应结果看，保护轴承气隙越大越好[72]，但也需要综合考虑电磁力控制范围以及保护轴承对磁轴承的保护作用。

(7)零间隙轴承、间隙自消除轴承、双层保护轴承以及混合动力轴承等新结构设计经检验能够有效降低转子跌落后带来的不良结果[49，51-53]。

(8)波纹带阻尼、弹性环、公差环等外加结构合适添加在保护轴承中，也能有效降低跌落后的作用结果[28，67]。

(9)必须避免气流驱动造成的球轴承的无载荷转动，这会造成保护轴承的失效[15]。

5 未来展望

转子跌落在保护轴承产生的瞬时大冲击力会造成磁轴承转子系统的损伤甚至是破坏，降低了设备运行的安全性与可靠性，大大增加了运行维护成本。对于磁轴承跌落在保护轴承上的动力学行为这一工程问题的未来发展，必然需要结合工程实际需求，解决在跌落碰摩过程中发生的由非线性动力学过程带来的损伤和破坏性问题，增加系统的安全可靠性，延长磁轴承系统的使用寿命。就目前的研究而言，未来的研究可以从模型建立、计算方法和工程中轴承结构与参数优化等三个方面来考虑。

(1)在模型建立方面，目前绝大多数研究中的局部力学模型大多采用了线性接触模型以及库仑摩擦力模型，未充分考虑转子跌落时保护轴承与转子的接触材料特性、相对运动速度、摩擦热效应以及接触磨损等因素。考虑多因素的模型一方面形式较为复杂，另一方面可行性及普适性不够高，后续的研究可以进一步考虑如何在模型多参变量和模型与真实工况贴近程度之间做平衡，基于保护轴承与转子跌落过程的相互作用特性，建立反映实际工程力学作用过程的径向接触力和切向摩擦力模型，给出准确表达形式并能够通过理论或实验给出符合实际的各项参数。在接触力学模型之外还可以进一步考虑一些重要的有实质影响的力学因素如空气动力、交叉耦合力[16]、剩磁、转子内部流体力[66]以及轴向力等，特别是轴向力在近年的研究中已经发现其容易引起转子前旋、表面磨损及能量损耗[66，74，78]。同时，工程中还可能出现磁轴承瞬态失效后恢复作用的情形，此状况下可利用磁轴承实现对跌落转子的再控制，过程中的最佳作用机制值得深入研究。

(2)在计算方法方面，目前对转子模型和轴承模型都有了深入的研究，包括转子的有限元模型和轴承结构的细化模型，但仿真建模的计算参数如何能真实反映实际工程中的结构参数，此部分未有深入研究。特别是有限元转子模型方面，转子的结构参数如各节点连接刚度阻尼等参数主要都直接经由研究者给出的值，此数据为经验值或试验值未有说明。后续研究人员可从此方面入手进一步研究，考虑如何经由理论建模计算或程序化试验得到真实可信、切实可用能直接反映真实工况下转子和轴承参数的结果，推动建模与实际工程紧密结合，真正解决工程应用需求。同时，建模发展需兼顾计算效率与结果准确度，文献[48]中通过迭代计算需要花费大量算力，如文献[78]所言，复杂模型以牺牲数值效率为代价，需通过模型简化、降阶等方式实现结果准确性和数字效率之间的平衡。

(3)在轴承结构与参数优化方面，降低转子跌落过程中的冲击作用和增强保护轴承的抵御冲击能力是问题的关键。降低冲击作用方面可以从保护轴承结构出发，研制更多新式结构的保护轴承(如零间隙轴承[49]、变形自适应轴承[53]、滚动—滑动一体化轴承[75]等)以降低转子跌落过程的相互作用，提高保护轴承-转子系统整体安全性；或者从材料参数出发，选用低摩擦因数、高阻尼系数材料减小跌落响应过程中出现涡动和大冲击的概率。增强保护轴承的抵御冲击作用方面，可以从轴承材料特性等方面出发，针对转子跌落响应作用中可能出现的短时大冲击和持续大载荷情形，研制能承受更高破坏应力、更耐磨损、更长疲劳周期的轴承材料，提高保护轴承自身抗冲击能力。同时，目前研究中新材料的发展使得主动保护轴承研制成为可能，这类新型保护轴承能够反馈跌落过程的相互作用并可以结合新的控制策略对跌落转子实现主动控制[77]，将极大可能降低跌落碰摩对系统带来的损伤。目前，基于主动保护轴承的研究尚未深入，存在较大的研究空间和研究价值。

6 结论

转子跌落在保护轴承上相互接触之后可能发生跳动、摆动、前向涡动、后向涡动等动力学行为，摩擦损耗、能量积聚、冲击作用等会对转子和保护轴承造成局部损伤，降低机械的使用寿命，严重的甚至会使设备受到破坏，因此研究转子跌落在保护轴承上的非线性动力学对磁轴承系统的安全运行至关重要。本文综述了近30多年来磁悬浮转子跌落在保护轴承上的动力学研究，从多方面较为全面地概述了目前转子跌落研究的历史进展，概括来看可得到以下几个结论：

(1)保护轴承与转子的局部接触力学模型目前研究主要采用的是赫兹接触模型和库仑摩擦模型，在选用合适参数后都能一定程度上有效模拟转子跌落后的动力学过程。考虑多因素的接触模型和摩擦模型形式上较为复杂，目前仿真中使用较少，后续研究者可尝试进一步结合复杂接触模型和摩擦模型研究转子跌落响应问题。

(2)跌落系统的转子的结构模型经历单平面转子、多自由度动力学模型以及有限元模型的发展，模型复杂度在研究中不断提升。复杂度的上升使模型更加贴合工程应用实际，但同时将使仿真计算时长增加，数值效率降低，因此，后续研究应兼顾模型复杂度和数值计算效率，可考虑寻求对高阶复杂模型有效降阶的方法，在不牺牲结果准确度的前提下提高数值效率。

(3)保护轴承对转子跌落响应结果至关重要，近年来涌现出了大量保护轴承的结构创新设计，许多保护轴承的新型结构大幅降低了转子跌落后的作用力及全周涡动的可能性。目前来看，重点集中在引入阻尼件(如波纹带、公差环)、消除保护间隙(如间隙自消除、零间隙轴承)、考虑轴向受力(如RAIAB)等，后续研究可参考前述设计思路进一步开展新型保护轴承结构设计。

(4)通过保护轴承的物理参数调整设计，如保护轴承支承刚度、支承阻尼系数、摩擦因数等方面，也能有效降低由于转子跌落对系统的损伤。针对保护轴承设计选用，本文经过总结归纳从材料特性、结构设计等方面给出了部分行之有效的保护轴承选用原则。