多通道多分量分解方法在变转速工况齿轮故障特征提取中的应用
2022-11-01田泽宇陈向民廖力达吴家腾
张 亢 田泽宇 陈向民 廖力达 吴家腾
1.长沙理工大学能源与动力工程学院,长沙,4101142.湖南大学机械与运载工程学院,长沙,410082
0 引言
旋转机械的振动信号包含了机械设备中零部件的健康状态信息。对振动信号进行分析和处理是从振动信号中提取故障特征的重要手段,而故障特征是对旋转机械进行故障状态判断与预测的依据[1]。齿轮是应用广泛的旋转机械部件,当其发生故障时,故障激励会导致振动信号产生调制现象,使得振动信号呈现非平稳的多分量调制特征[2-3]。要提取故障特征就需要减小噪声和其他分量的干扰,从中分离出调制成分。然而实际中,齿轮所在齿轮箱结构的复杂性以及运行工况的波动性会使传感器测得的振动信号包含复杂的耦合成分[4],且振动信号的分量可能跨多个频带或同一频带包含多个分量,以及分量在支撑域重叠,从而造成调制成分分离困难[5]。
目前主要通过对振动信号进行分解来分离调制成分。根据信号分解实现方式的不同,现有分解方法主要可分为时域分解方法、频域滤波分解和时频域重构方法。经验模态分解[6]、局域均值分解[7]、本征时间尺度分解[8]等递归式时域分解方法得到了大量应用,这一类方法以信号的时间尺度特征为基础,而时频域重叠的多分量信号在同一时间尺度上分布着多个分量,此类方法会将其识别为单个分量而无法分解;频域滤波方法以频带划分为基础,如奇异谱分解[9]、小波包变换[10]、变分模态分解[11]等,该类方法对频带的划分是机械的格型划分,缺乏自适应性,另外对于跨多个频带的分量信号,会被分解到不同的频带之中,从而失去物理意义;时频域重构方法通过将目标分量所在的时频支撑域之外的时频分布系数置零,达到分离各分量的目的,如同步压缩变换[12-13]等。这类方法具有锐化的时频脊线,提高了时频的可读性,然而当信号分量在时频域发生交叉时,由于交叉部位拥有相同的时频分布系数,故无法对其进行分解或错误分解。
根据上述分析,对于分解具有复杂时频特征的非平稳信号,不能仅仅以信号的时频域局部特征为基础,而是要找到既能独立代表分量又不受时频特征影响的物理量作为分解的依据。最近,STANKOVIC等[14]提出了一种新的多通道多分量非平稳信号分解方法(MMD),该方法将信号中的分量用一组权重系数加权的向量线性组合表示,并以时频聚集性度量值为优化目标,通过迭代优化得到各个分量的权重系数组,从而获得相应的分量信号。MMD方法与前述以时频局部特征为分解依据的分解方法相比,其本质不同在于将信号中的分量表示成一个由权重系数加权的向量,而不同的分量具有不同的系数组合,因此,理论上,对跨多个频带或单个频带中有多个分量以及分量信号发生了交叉的复杂信号也能进行分解,特别适合具有多分量调制特点且由于多激励源耦合造成时频分布复杂的齿轮箱振动信号的分析。目前,MMD方法仅应用于仿真信号的分析[15-16],而对于高采样率的实际振动信号,进行时频聚集性度量的计算量很大,从而导致MMD算法的分解时间长,实用性差。因此,要利用MMD方法分析实际振动信号,必须解决原算法中时频聚集性度量计算量大的问题。对数窗能量准则[17]通过折中选取最佳窗长,降低时频矩阵的规模,减少算法迭代次数,从而可间接降低时频聚集性度量的计算量与时长。
综上,本文在将对数窗能量准则融入MMD方法、提高MMD方法计算效率的基础上,通过仿真信号将MMD方法与传统的基于时间尺度的分解方法进行了对比,证明了其优势。进一步,利用这种全新的方法,从复杂的变转速工况齿轮箱故障振动信号中分离含有故障调制成分的分量信号,并从中提取故障特征,从而为变转速工况齿轮故障特征提取提供了一条新的途径。
1 MMD方法
对于任意一组多通道多分量信号x(n),MMD方法将x(n)中的每一个分量信号看作若干个特征向量的线性组合,通过优化迭代获得该线性组合的权重系数,便可得到x(n)相应的分量信号,其具体步骤如下:
(1)将x(n)写成
(1)
其中,x(m)(n)(m=1,2,…,S)代表第m个通道信号(即传感器测得的数据),每一个通道信号实际上都是一组多分量信号;xp(n)=Ap(n)ejφp(n)(p=1,2,…,P)表示第p个分量成分(即系统产生的源信号),Ap(n)和φp(n)分别为瞬时幅值和瞬时相位;αmp和φmp分别为源信号经传感器改变的幅值和相位。通过式(1)可以看出任意一个传感器信号可以由源信号分量的线性组合来表示。
将式(1)进一步写成矩阵形式:
Xsen=AXcom
(2)
其中,xp(p=1,2,…,P)表示分量信号xp(n)的向量形式。传感器信号矩阵为
Xsen=[x(1)(n)x(2)(n) …x(S)(n)]T
系统产生的分量信号矩阵为
Xcom=[x1(n)x2(n) …xP(n)]T=
[x1x2…xP]T
常系数转换矩阵为
将系统产生的信号分量转换为传感器测得的信号。
(2)计算Xsen的自相关矩阵R:
(3)
其中,(·)H表示矩阵的Hermitian转置,自相关矩阵R为一个方阵。
(3)对自相关矩阵R进行特征值分解:
(4)
其中,矩阵U为特征向量矩阵;Λ为特征值对角阵;λp为特征值;up为对应的特征向量。由式(3)和式(4)可以看出,特征向量up可以用传感器信号的线性组合表示,由上文已知传感器信号是源信号分量的线性组合,从而可以将特征向量up用源信号分量的线性组合表示,即
(5)
当S≥P时,由式(5)可以知道,每个分量信号xp同样可以由特征向量的线性组合表示,即
xp=η1pu1+η2pu2+…+ηPpuP
(6)
其中,ηip(i=1,2,…,P)为未知的权重系数。
(4)因为不同信号成分在时频面上的时频聚集性不同,所以可以用时频聚集性来判断信号成分。信号在时频域的支撑区间的面积可以定量描述信号的时频聚集性。设每个分量信号xp在时频域的支撑区间为DTp,其面积为Dp,如果分量有重叠,那么其支撑区间必然也会重叠,但实际中支撑区间一般不会完全重叠,因此不失一般性,假设D1≤D2≤…≤DP。信号时频分布的Lq范数可用来表示信号在时频面上支撑区间的面积,即Lq范数可以作为聚集性测度值M{·}来度量信号的时频聚集性,即
(7)
其中TFR(n,k)表示信号的时频分布。因为短时傅里叶变换(short time Fourier transform,STFT)具有计算简单、不会产生交叉项干扰等优点,且得到了成熟应用,因此,本文将STFT作为信号的时频表示。
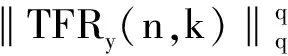
(8)
i=1,2,…,P
那么将此时的权重系数ηi1代入式(6),便可得到第一个分量信号x1。
式(8)实际上是一个优化问题,即以y的时频聚集性测度最小为优化目标,在保证‖y‖2恒定的情况下,利用具体的优化算法计算相应的未知权重系数ηi1。本文采用遗传算法来求解该优化问题。
(6)由式(6)可知,x1=η11u1+η21u2+…+ηP1uP,将第一个分量信号x1替换为第一个特征向量u1,然后将u1(即x1)从剩余的特征向量uk(k=2,3,…,P)中去除,即
(9)
此时得到了一组新的特征向量us(s=1,2,…,P),形成新的线性组合y=β1u1+β2u2+…+βPuP;对y重复步骤(5),可得到第二小的支撑区间面积D2对应的权重系数ηi2(i=1,2,…,P),将ηi2代入式(6)即可得到第二个分量信号x2;将x2替换特征向量u2,并从剩余的特征向量uk(k=3,4,…,P)中去除,依此类推,整个过程是一个迭代优化的过程,直到没有新的特征向量us产生,代表信号中所有的分量xp(p=1,2,…,P)被分解出来,此时迭代终止。
从上述分解过程可以看出,每一个分量信号都是不同权重系数加权的特征向量的线性组合,其中特征向量来自于信号自身构成的矩阵,即整个分解过程是不需要先验知识的,而表示每个分量的特征向量的线性组合是唯一的,这确保了得到的分量信号是不重复的;此外,以时频聚集性测度最小为优化目标,通过迭代优化获得权重系数,这保证了每一个特征向量的线性组合只对应了一个单分量信号,而不是交叉分量或组合分量等虚假分量。
2 时频聚集性度量与仿真信号分析
2.1 基于对数窗能量准则的时频聚集性度量
在MMD方法中,一方面,时频聚集性度量的准确性决定了分解的效果;另一方面,以信号时频矩阵的范数值作为时频聚集性度量值,时频矩阵的规模会影响算法的计算量。而对于实际振动信号,因为其较高的采样频率会导致大维数的时频矩阵,所以会有很大的计算量。因此,如何保证时频聚集性度量准确的前提下又具有小的计算量,是MMD方法应用于实际振动信号分析的关键。
良好的时频分辨率是时频聚集性度量准确的前提[18],STFT的时频分辨率与窗长N和采样频率fs密切相关。对于实测振动信号,采样频率fs是预先设定的,窗长N决定了时频分辨率。本文通过对数窗能量准则Q(N)来自适应确定最优窗长:
(10)
其中,G(n,k)为信号的STFT时频分布;lgE(N)为窗能量E(N)的对数值;Mw为窗函数个数。因此,Q(N)实际上为信号STFT时频能量与窗函数能量的对数的比值。随着窗长N的增大,式(10)中分子分母增长速度的快慢不同,那么理论上Q(N)会在某些窗长发生折中,而当Q(N)在某个折中位置为最小值时,意味着STFT的时频聚集性在窗长范围内最优,那么此时对应的窗长N为最佳窗长[17-18]。
2.2 仿真信号分析
仿真信号s(t)如下:
(11)
它由3个分量组成,其中调幅分量s1(t)与线调频分量s2(t)在时频域发生了交叉,s3(t)为跨时频尺度的调制分量。
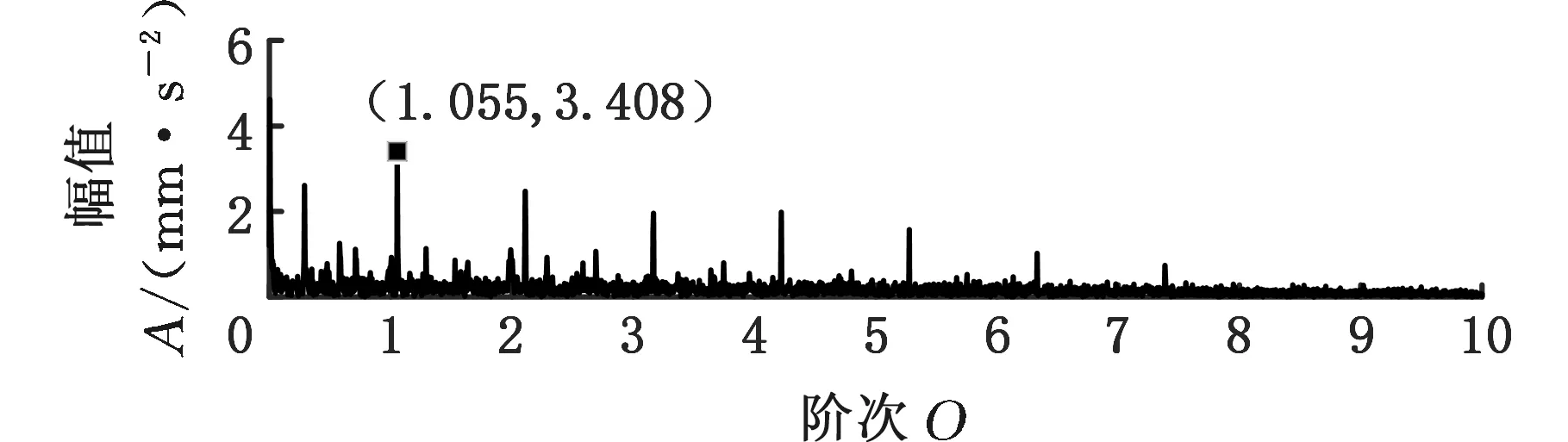
首先通过对数窗能量准则确定最优窗长,为考察准则的鲁棒性,设置采样频率分别为800 Hz、1000 Hz和1200 Hz,窗函数选用Hanning窗,窗长范围设定为8~256。根据式(10)计算不同采样频率下的对数窗能量准则曲线,如图1所示,可以看出,800 Hz、1000 Hz、1200 Hz采样频率下的最优窗长分别为95、119和137。
根据最优窗长对s(t)进行STFT,同时在相同采样频率下,选择一个较小和一个较大的窗长进行对比,结果如图2所示。可以明显看出,在不同采样频率下,都是根据最优窗长进行STFT时获得的时频效果最佳;另外,在采样频率为1000 Hz的情况下,分别选择不同窗长,在同一台计算机上针对仿真信号将MMD算法各运行了30次。统计循环迭代次数和平均计算时间两个指标,如表1所示。可以看出,相比于其他窗长,当采用对数窗能量准则确定的窗长119时,MMD算法的平均运行时间最短,迭代次数最少,说明了引入对数窗能量准则的必要性。
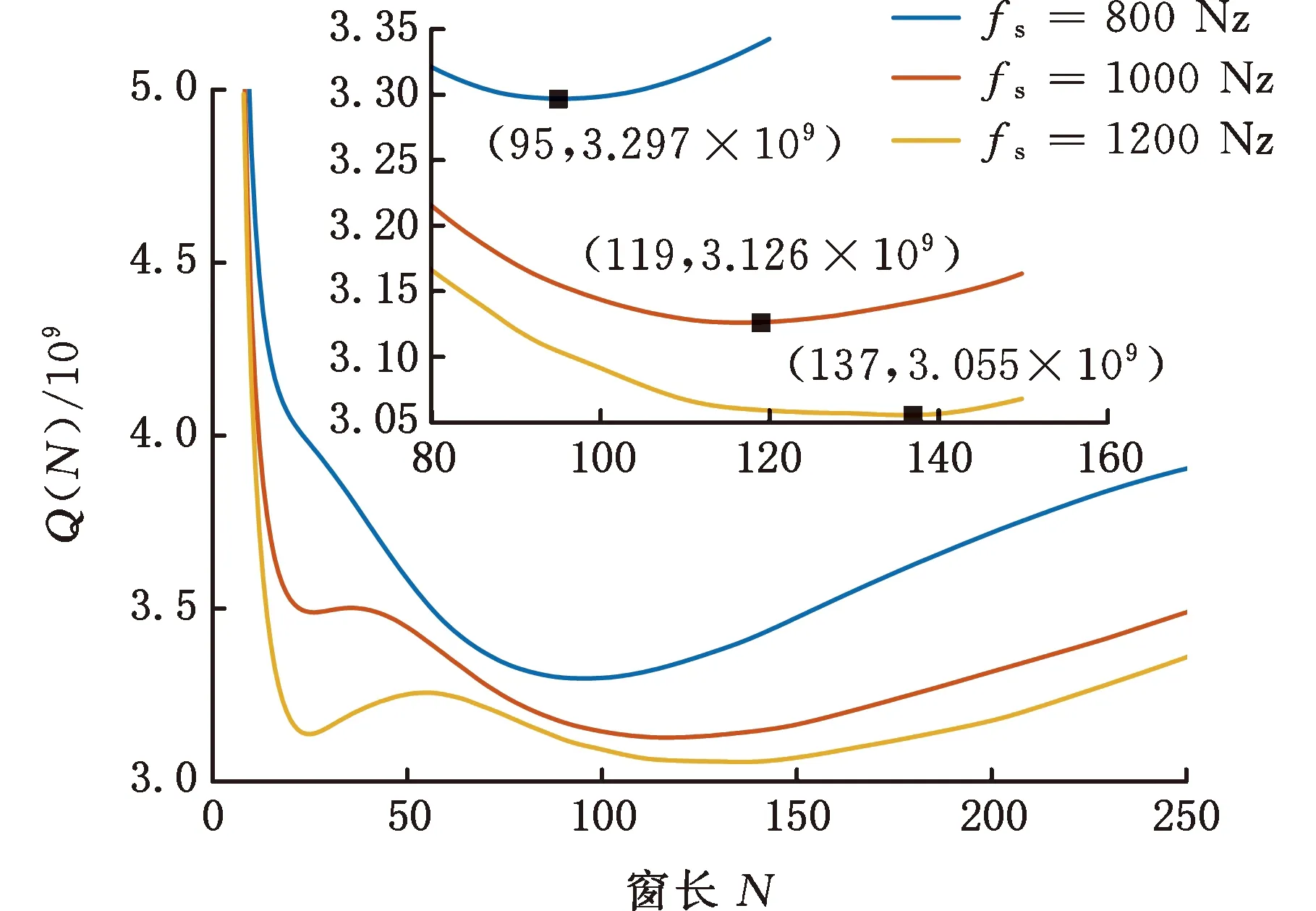
图1 s(t)在不同采样频率下的对数窗能量准则曲线Fig.1 Logarithm window energy rule curve of s(t) atdifferent sampling frequencies
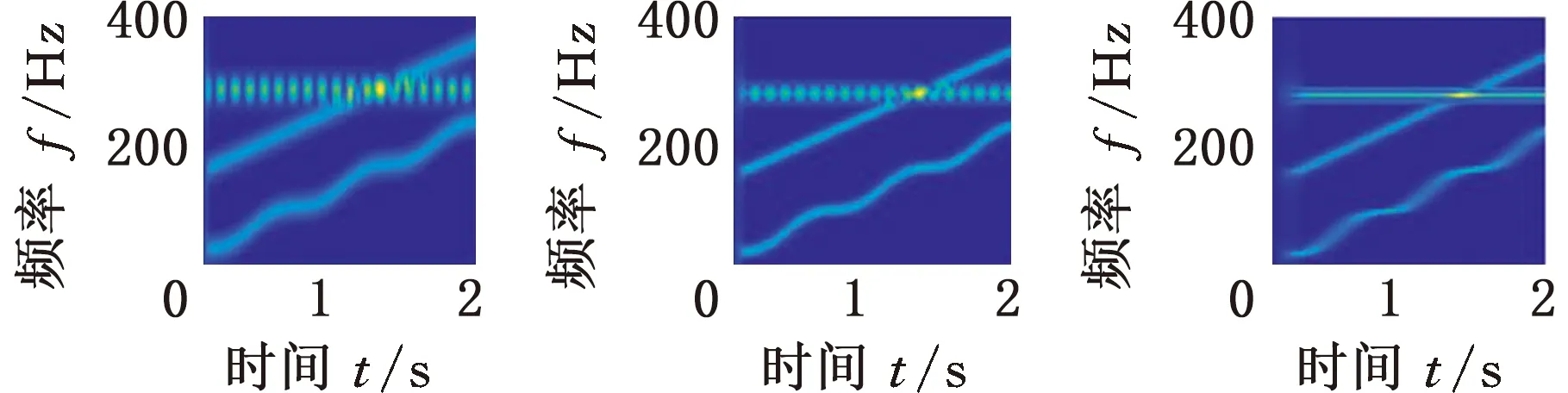
(a)fs=800 Hz,N=50 (b)fs=800 Hz,N=95 (c)fs=800 Hz,N=180
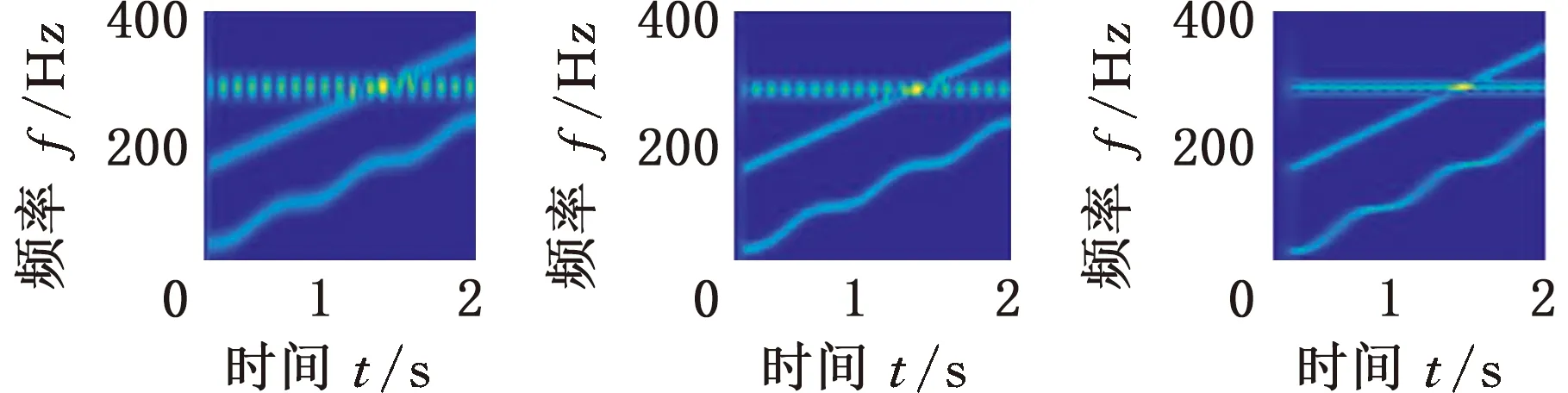
(d)fs=1000 Hz,N=95 (e)fs=1000 Hz,N=119 (f)fs=1000 Hz,N=209
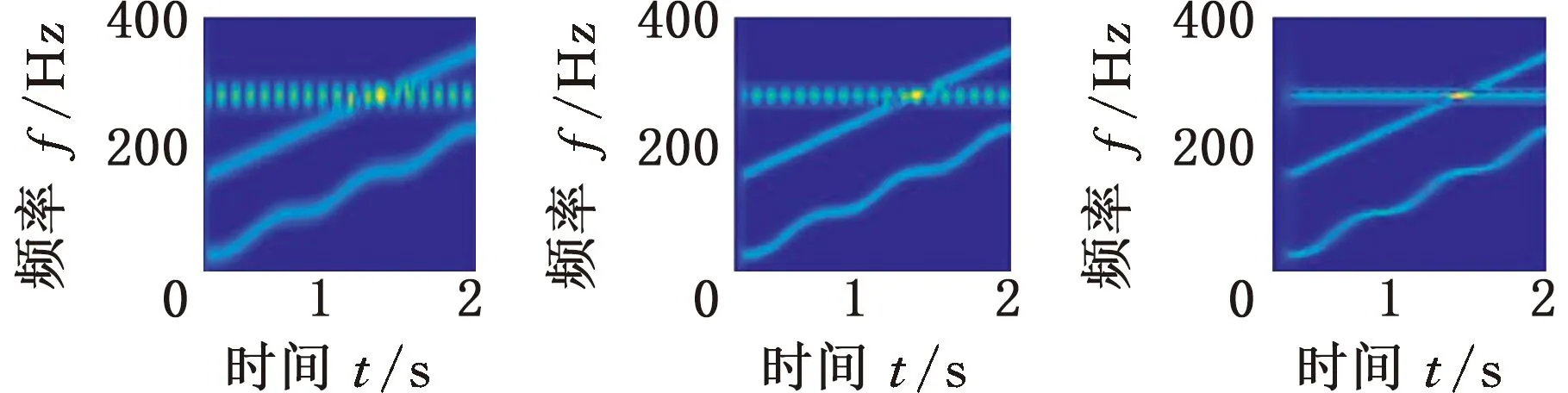
(g)fs=1200 Hz,N=119 (h)fs=1200 Hz,N=137 (i)fs=1200 Hz,N=210
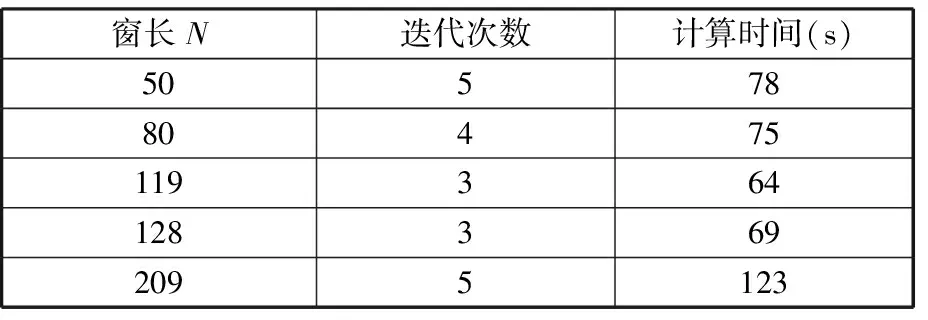
表1 不同窗长下MMD算法的迭代次数与运算时间
基于上述分析,将仿真信号s(t)的采样频率设置为1000 Hz,对应最优窗长为119,进行MMD分解。得到的自相关矩阵的特征值如图3所示,可以看出,非零特征值的个数为3,即P=3,正好等于s(t)的实际分量数。根据S≥P,取S=3,经过迭代分解,结果如图4所示。可以看出,交叉分量得到了很好的分离,得到的第三代特征向量准确地对应了仿真信号的3个分量,说明了MMD方法的有效性。
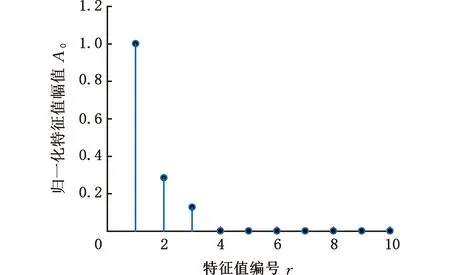
图3 自相关矩阵的特征值Fig.3 Eigenvalues of the autocorrelation matrix
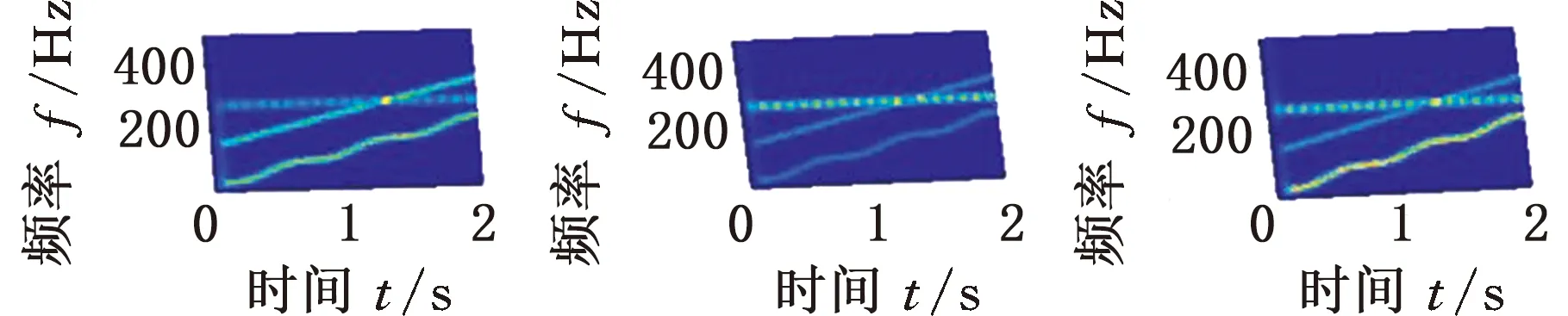
(a)初始特征向量
(b)第一代特征向量
(c)第二代特征向量
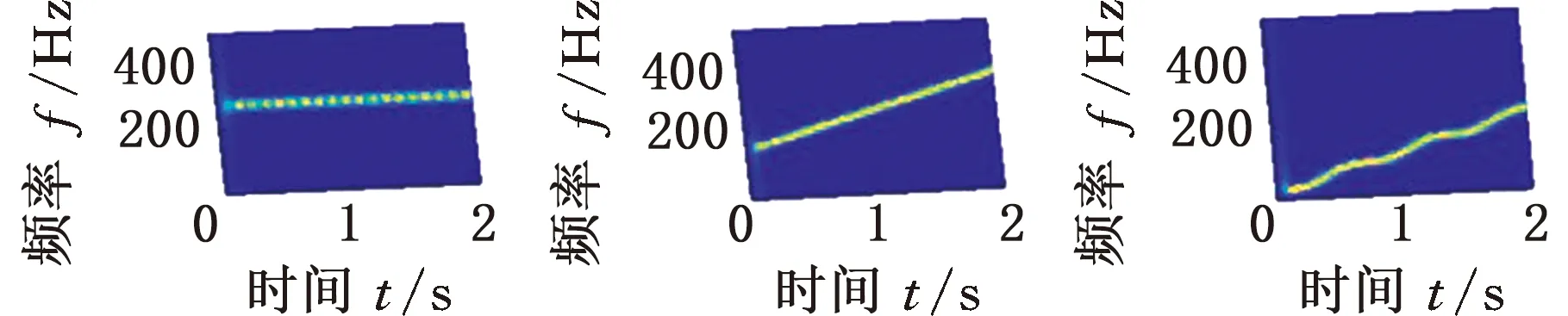
(d)第三代特征向量图4 仿真信号s(t)的MMD分解结果Fig.4 MMD decomposition results of simulationsignal s(t)
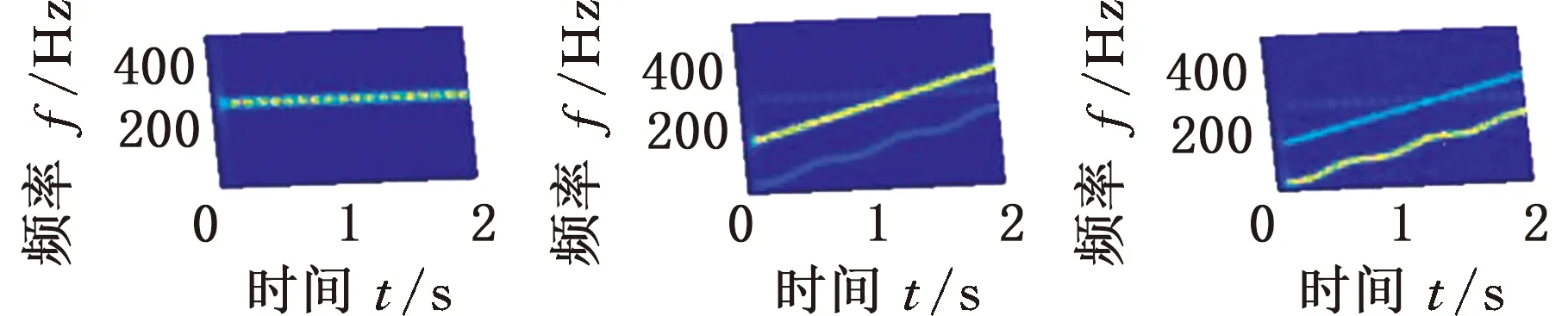
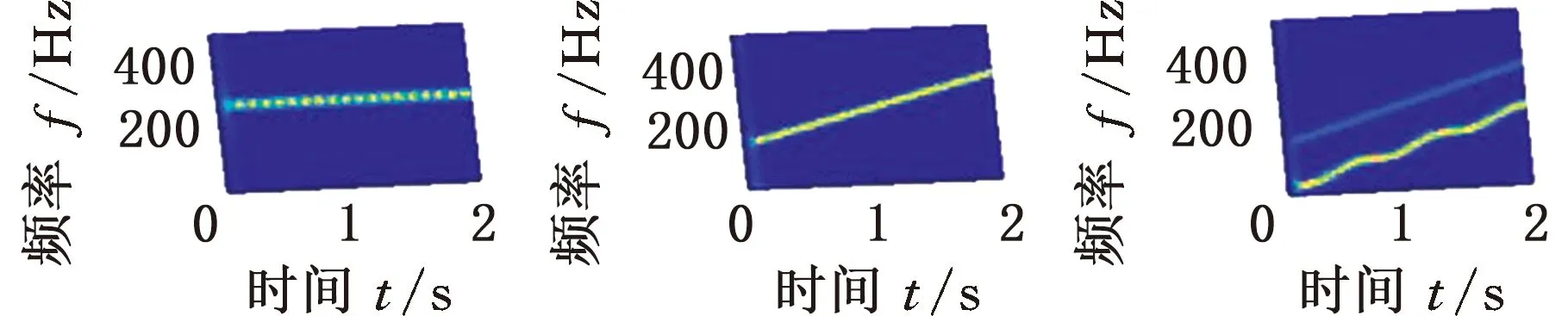
采用目前应用广泛的经验模态分解(empirical mode decomposition,EMD)和变分模态分解(variational mode decomposition,VMD)方法分解仿真信号s(t),为直观对比,分解结果也用STFT时频图表示。EMD与VMD分解得到的前3个分量如图5和图6所示。由图5可以看出,EMD将原信号中的交叉分量当成了一个分量,而非交叉分量也由于时间尺度跨度大,被分解为两个分量;由图6可知,VMD算法的频带划分清晰,原信号按频率被机械地分割到3个频带之中,得到的3个分量均失去了物理意义。对比结果进一步说明了MMD方法的优越性。
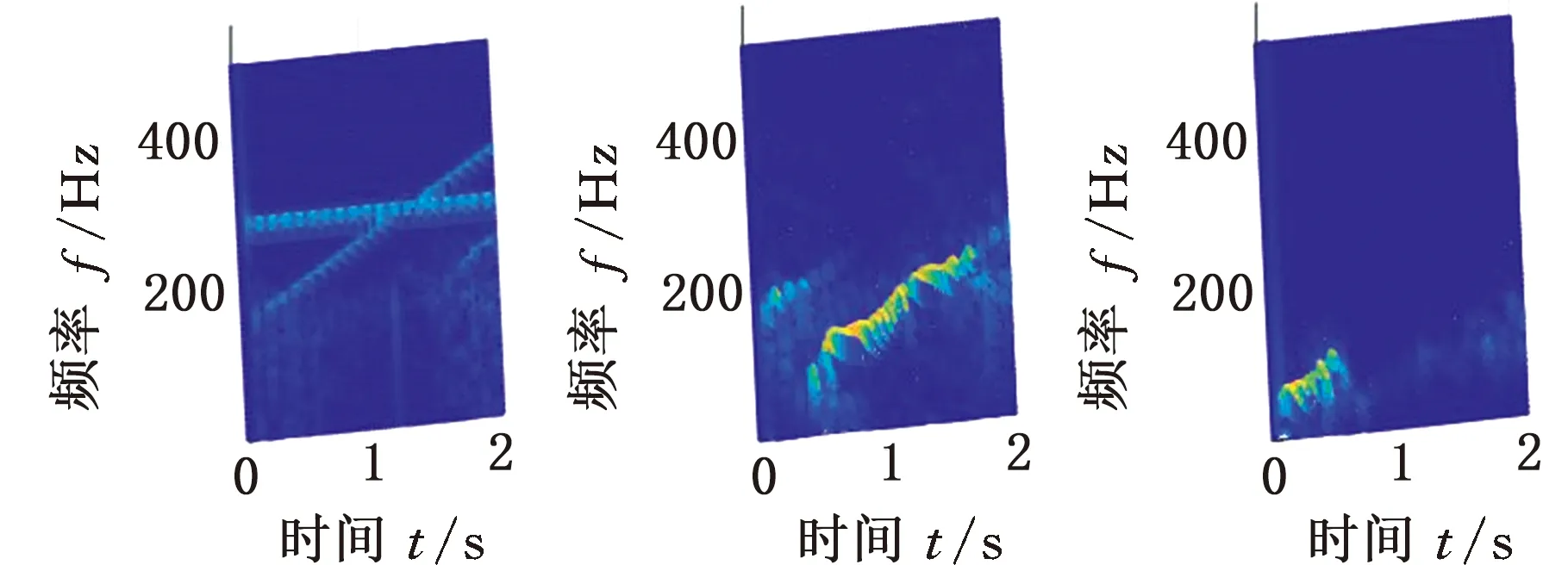
(a)IMF1 (b)IMF2 (c)IMF3图5 仿真信号s(t)的EMD分解结果Fig.5 EMD decomposition results of simulation signal s(t)
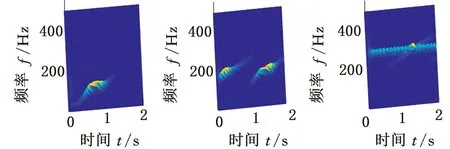
(a)BIMF1 (b)BIMF2 (c)BIMF3图6 仿真信号s(t)的VMD分解结果Fig.6 VMD decomposition results of simulation signal s(t)
3 在变转速工况齿轮故障特征提取中的应用
齿轮箱包含多种运动零部件,运行时存在多种振动形式,尤其是当工作在非稳态工况时,各个部件的固有频率振动成分与齿轮、轴承等旋转部件的啮合振动、故障冲击振动等成分在时频域很可能发生重叠。传统的以时间尺度特征为分解依据的方法无法分离这些成分,而根据仿真信号的分析MMD方法特别适合处理该类信号。本节首先利用MMD方法对变转速工况下的齿轮箱振动信号进行分解,将包含故障成分的分量从其他干扰分量和噪声中分离出来,然后通过谱分析提取故障特征。
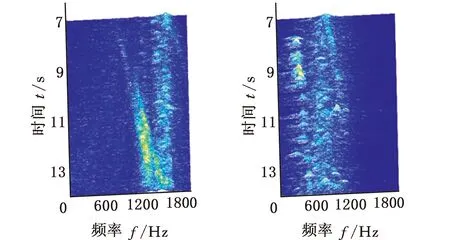
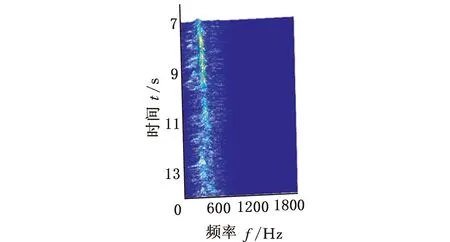
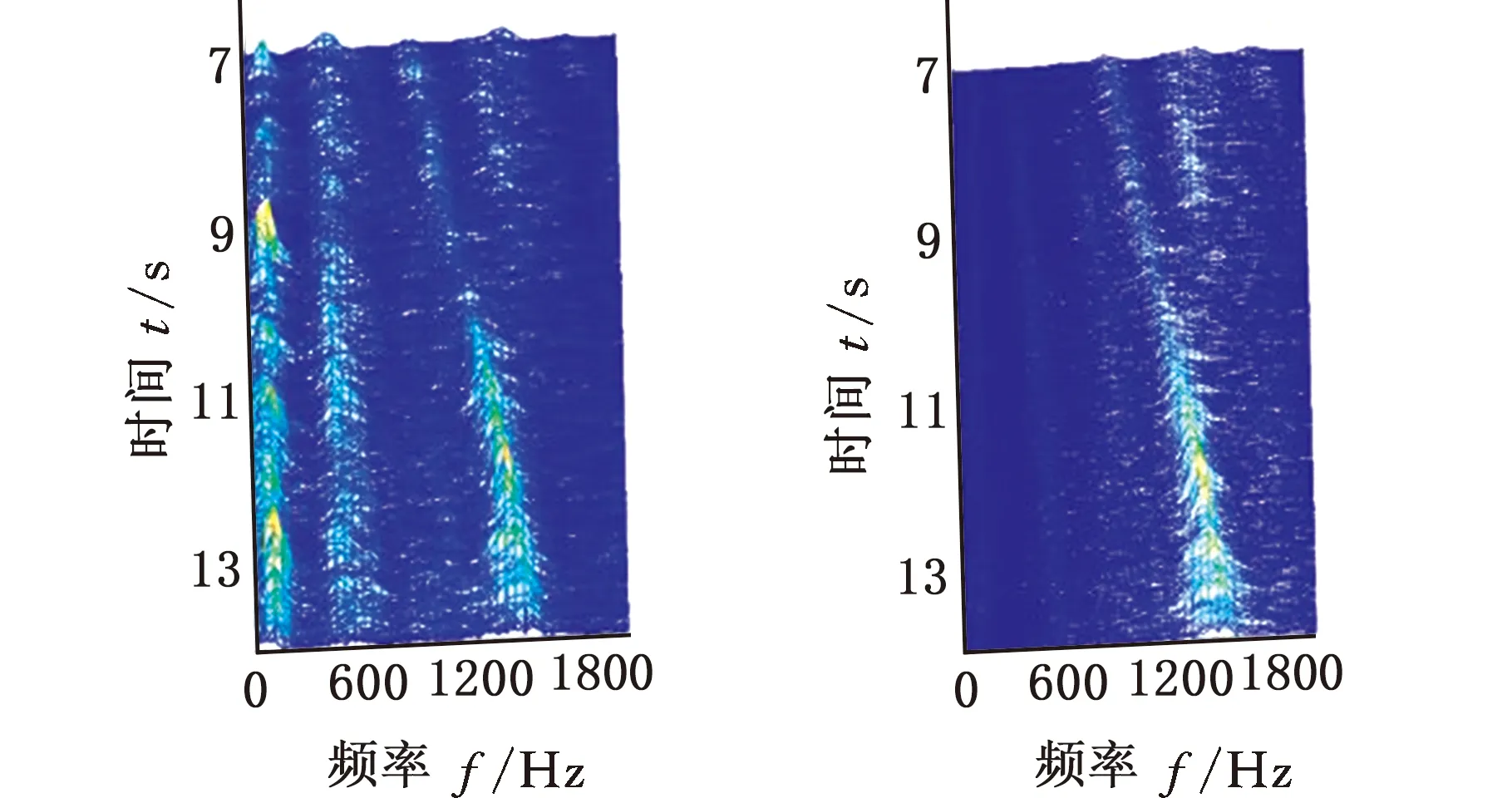
在SpectraQuest公司的旋转机械故障模拟综合实验台上进行变转速工况下齿轮故障实验,振动信号由5个PCB三向加速度传感器测取,共有S=15个通道,实验台以及传感器安装位置如图7a所示,数据采集设备为SIEMENS公司的LMS SCADAS Mobile多通道数据采集系统,如图7b所示。故障齿轮所在齿轮箱的结构如图8所示,转轴Ⅰ和转轴Ⅲ分别为输入轴和输出轴,齿轮1、2、3、4均为标准直齿轮,齿数分别为29、100、36和90。实验前,分别在齿轮1和3上设置了齿面磨损和断齿故障(实验1)。为验证变转速工况下分析效果,实验时输入轴转速从440 r/min增至3200 r/min,采样频率设置为4096 Hz,某通道的时域信号和转轴I的转速曲线如图9所示,其STFT时频图见图10a。可以看出,分布有包括随转速变化的齿轮啮合振动、故障冲击振动以及不随转速变化的部件固有频率振动等多种振动成分,且这些成分跨时间尺度特征大,成分之间存在多处交叉,分布复杂。

(a)旋转机械故障模拟综合实验台

(b)LMS SCADAS Mobile多通道数据采集系统图7 旋转机械故障实验台与数据采集系统Fig.7 Rotating machinery fault test bench and dataacquisition system
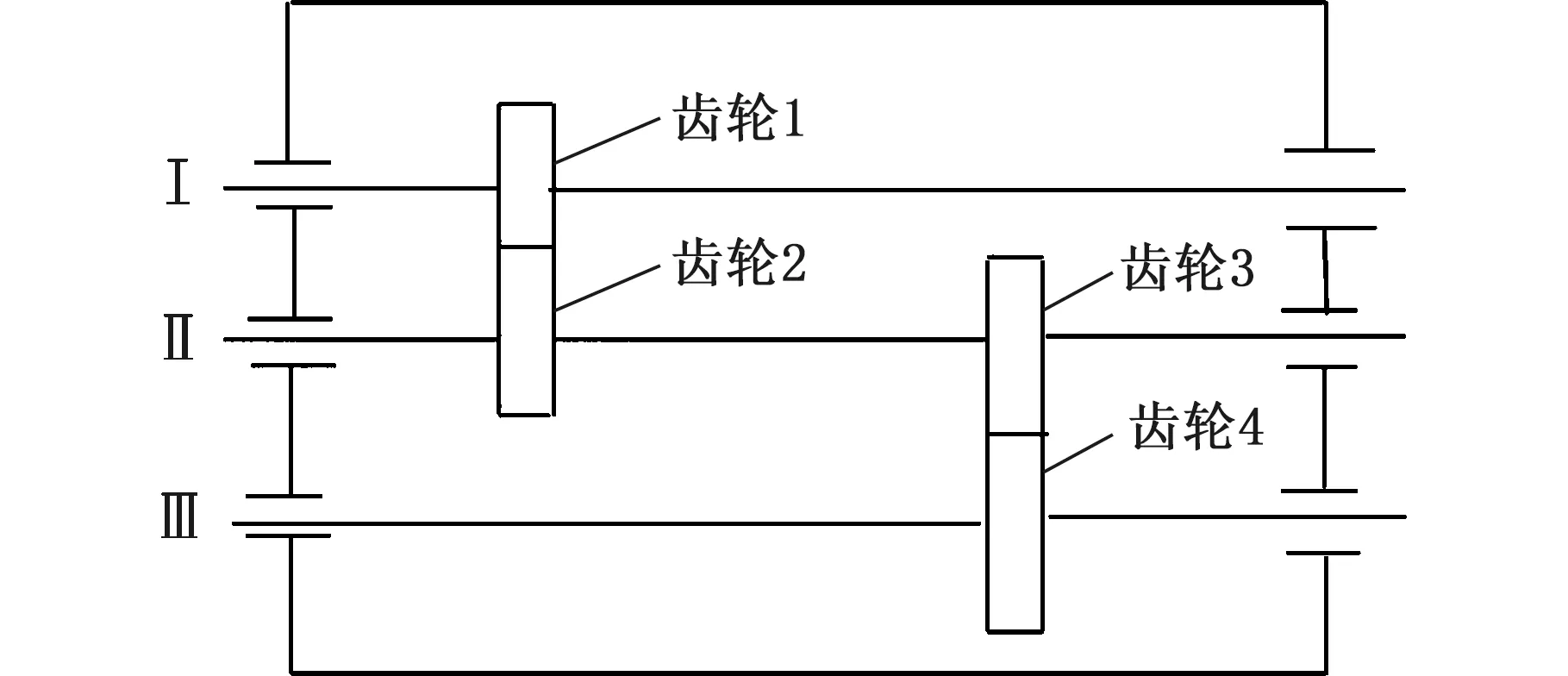
图8 齿轮箱结构简图Fig.8 Structural diagram of gearbox
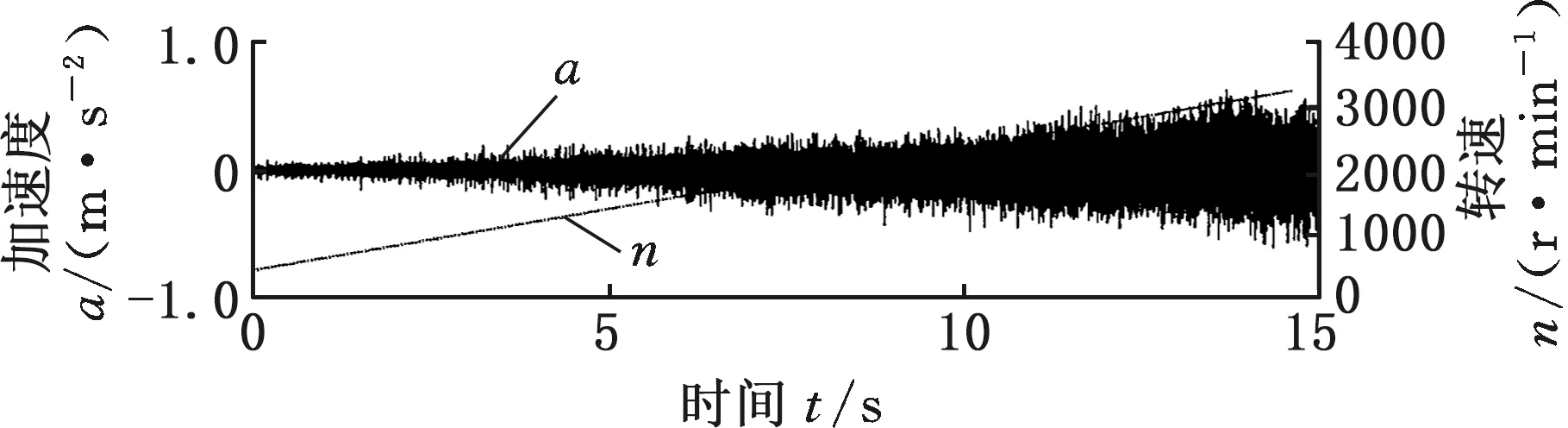
图9 某通道时域信号与转轴Ⅰ转速曲线Fig.9 Time domain signal of a channel and rotatingspeed curve of shaft Ⅰ
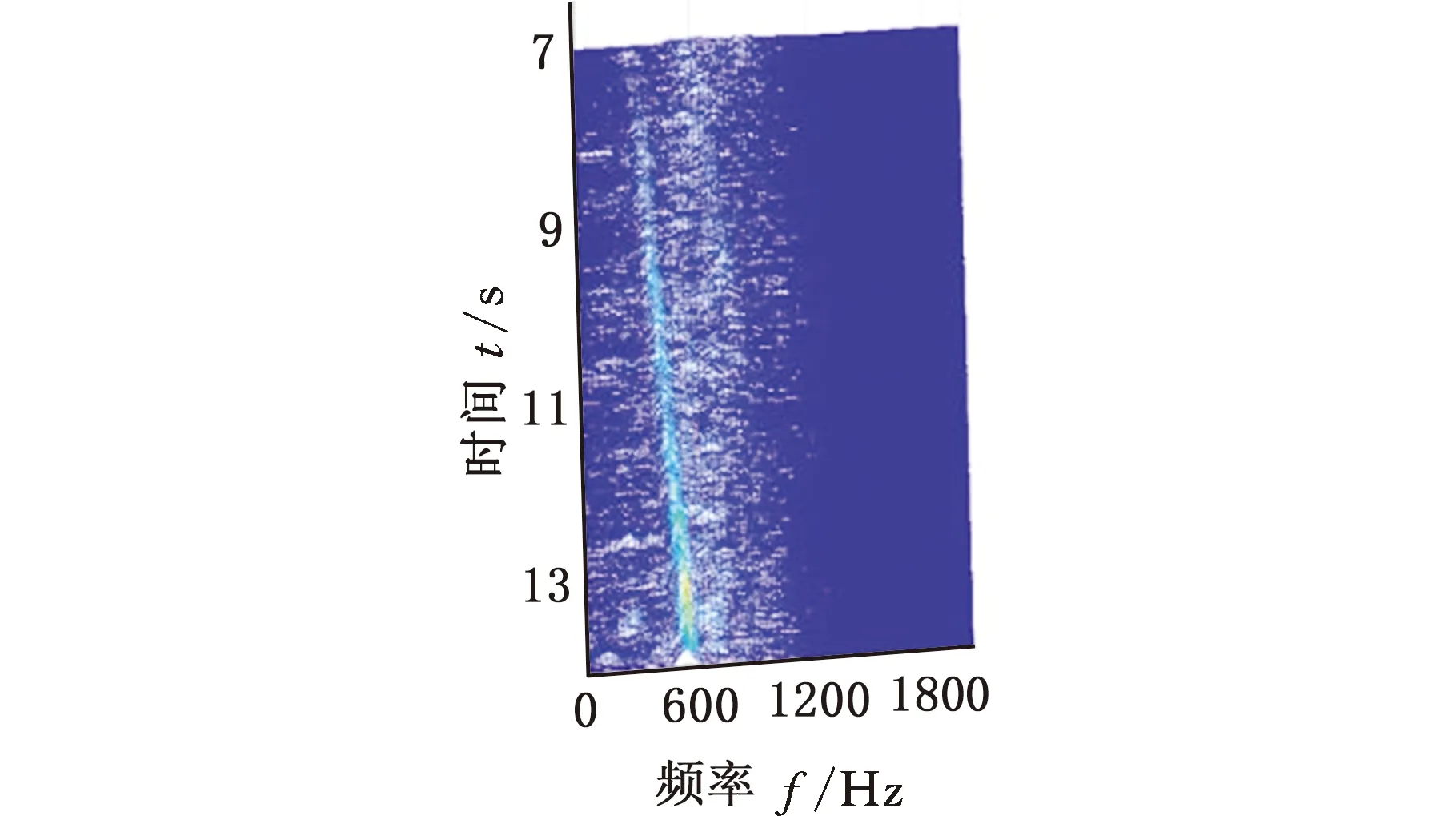
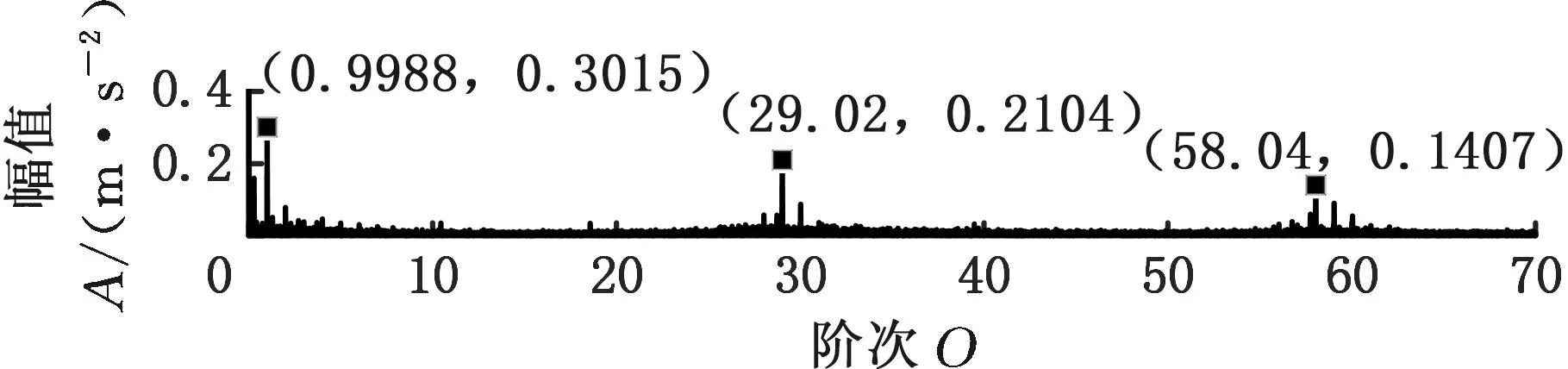
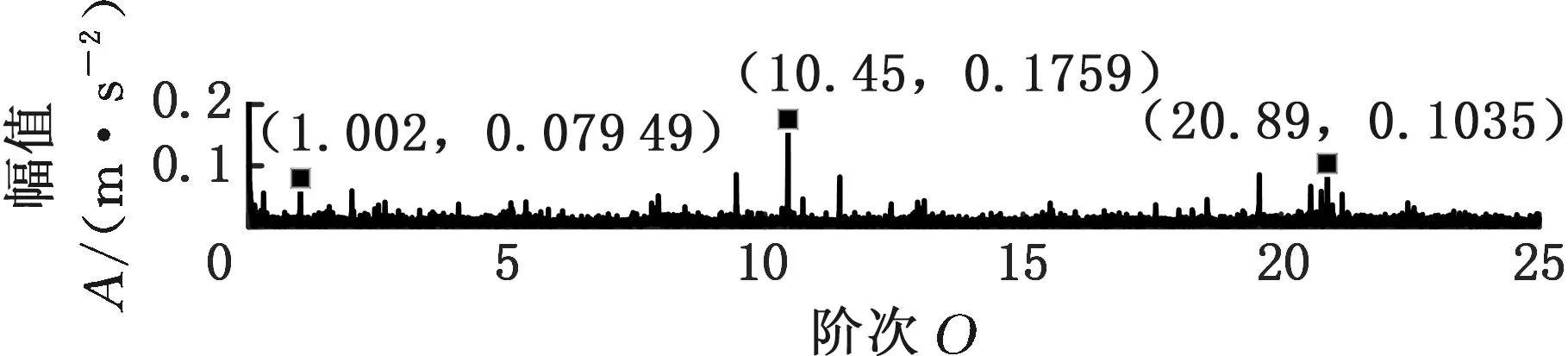
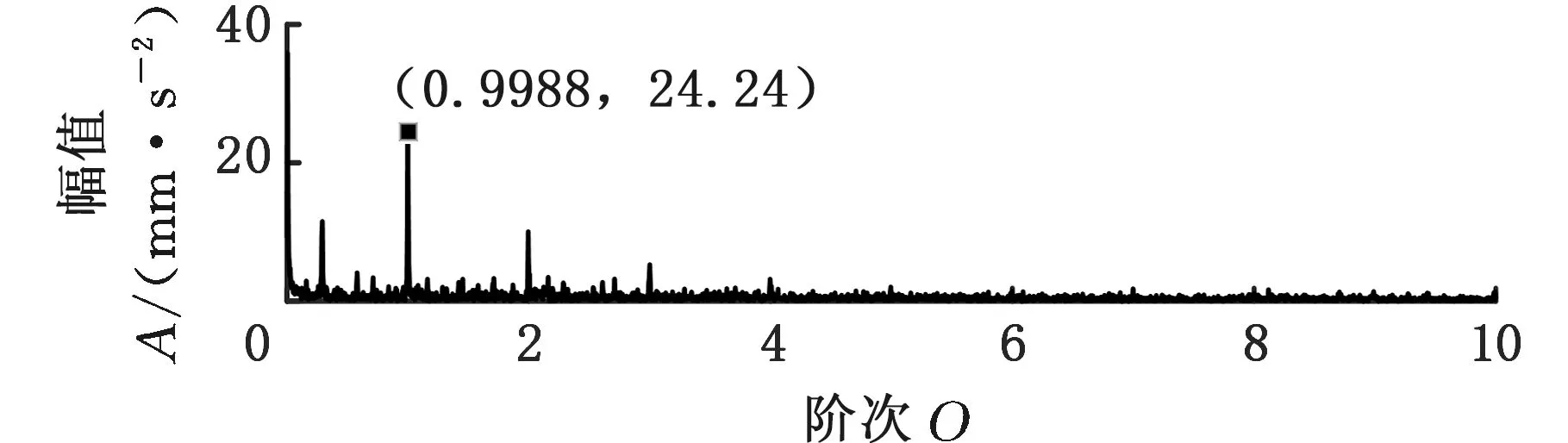
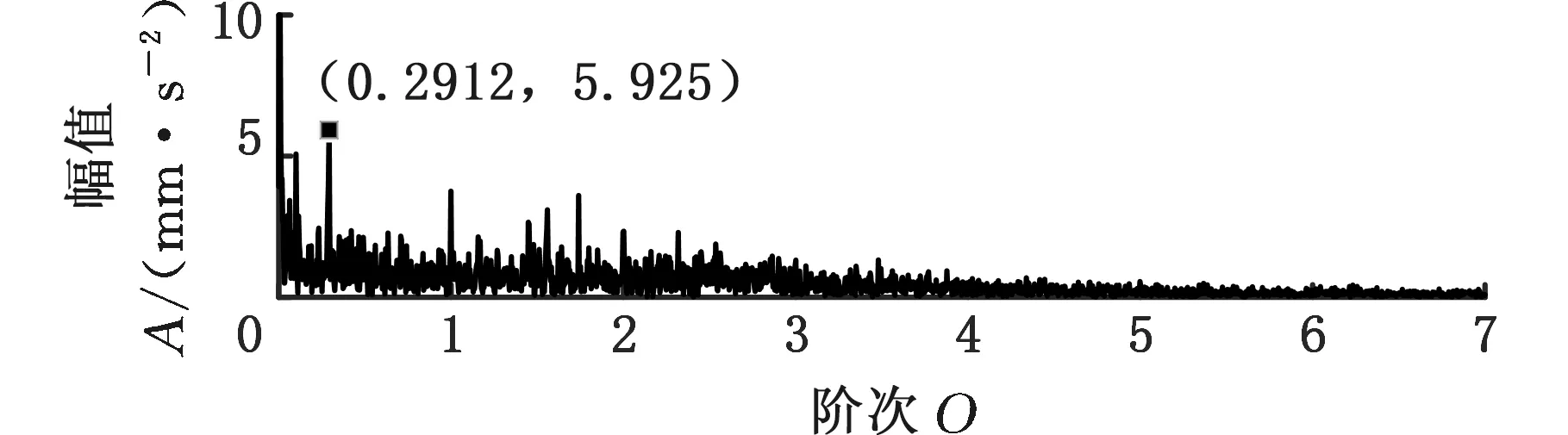
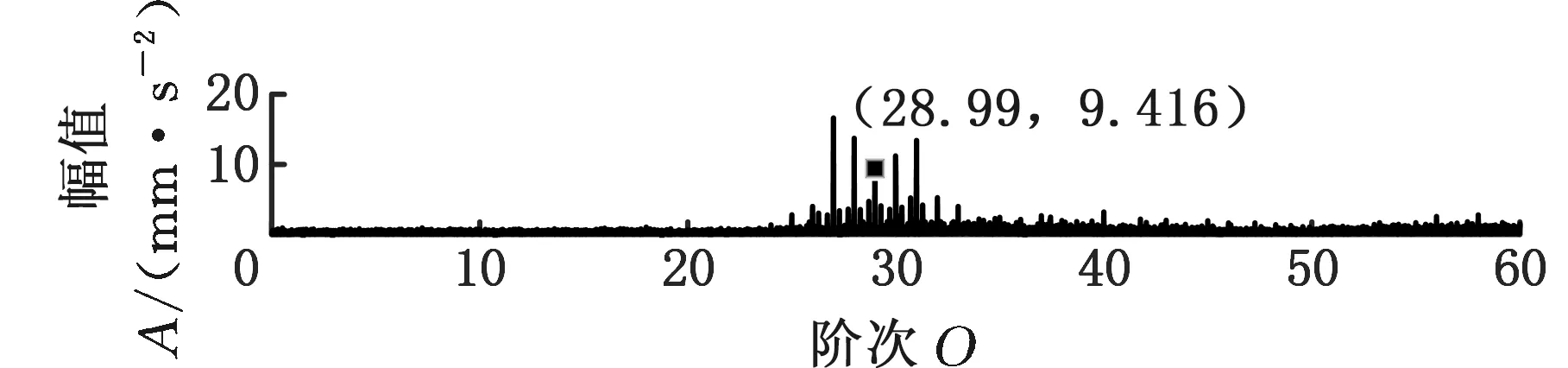
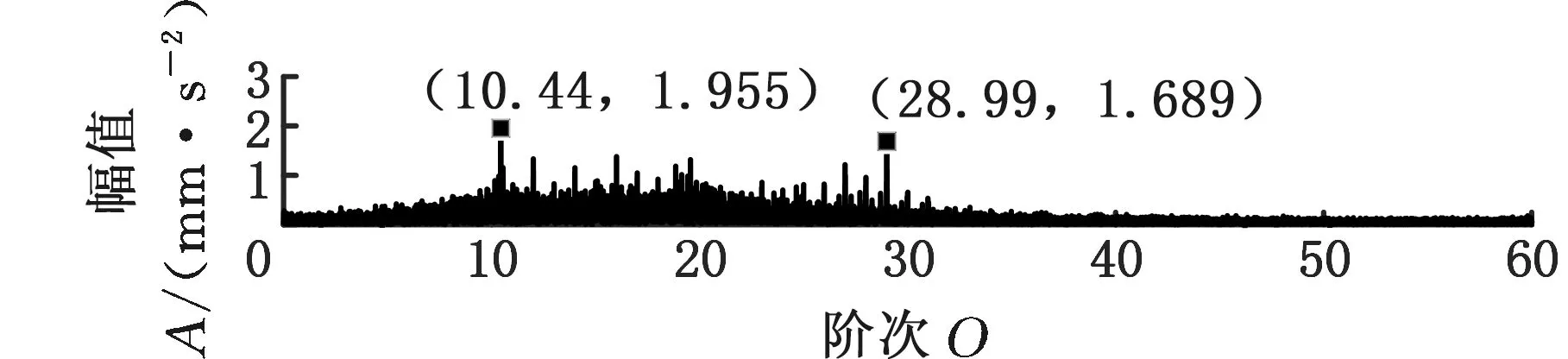
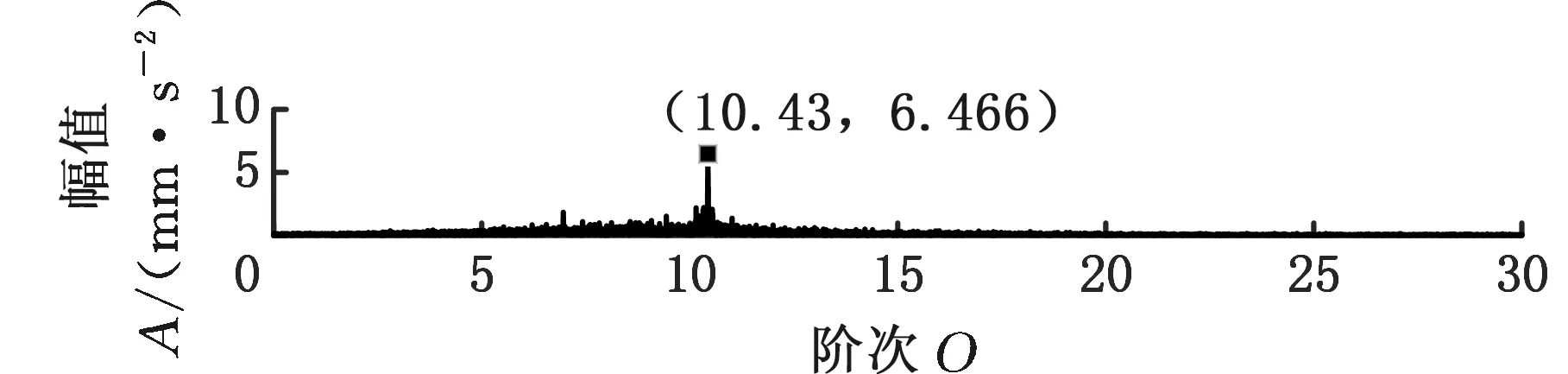
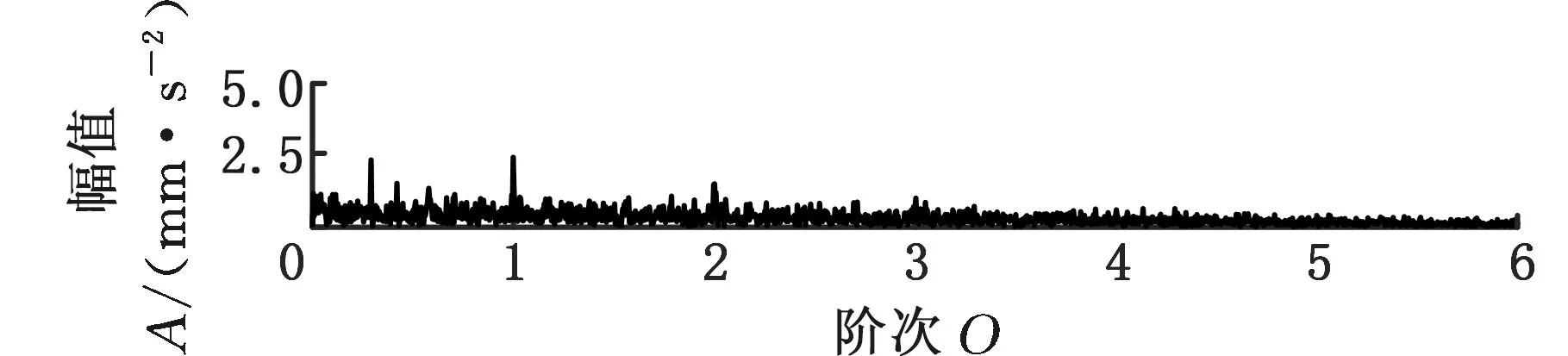
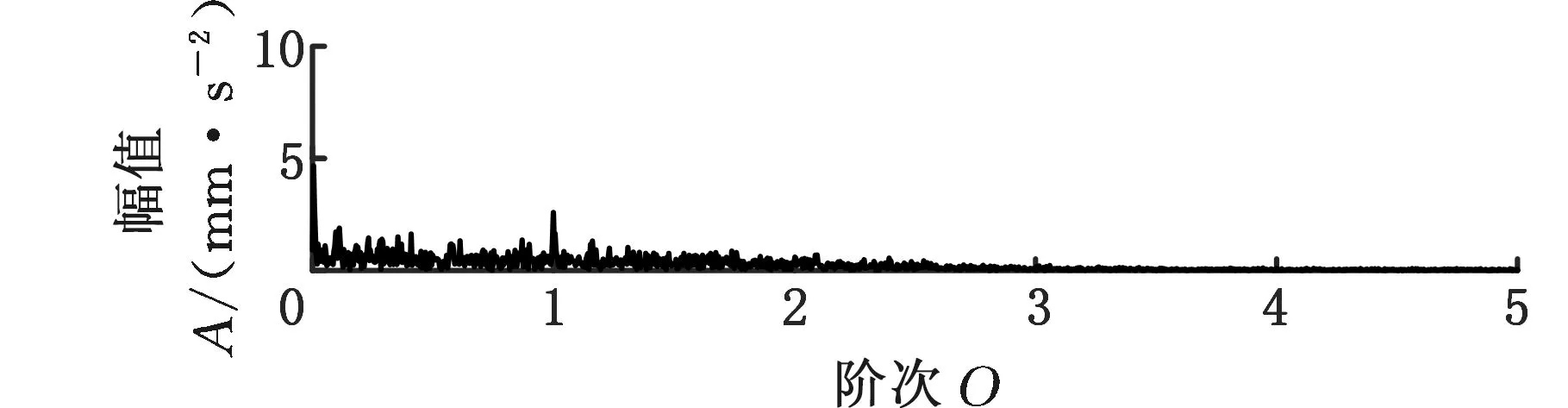
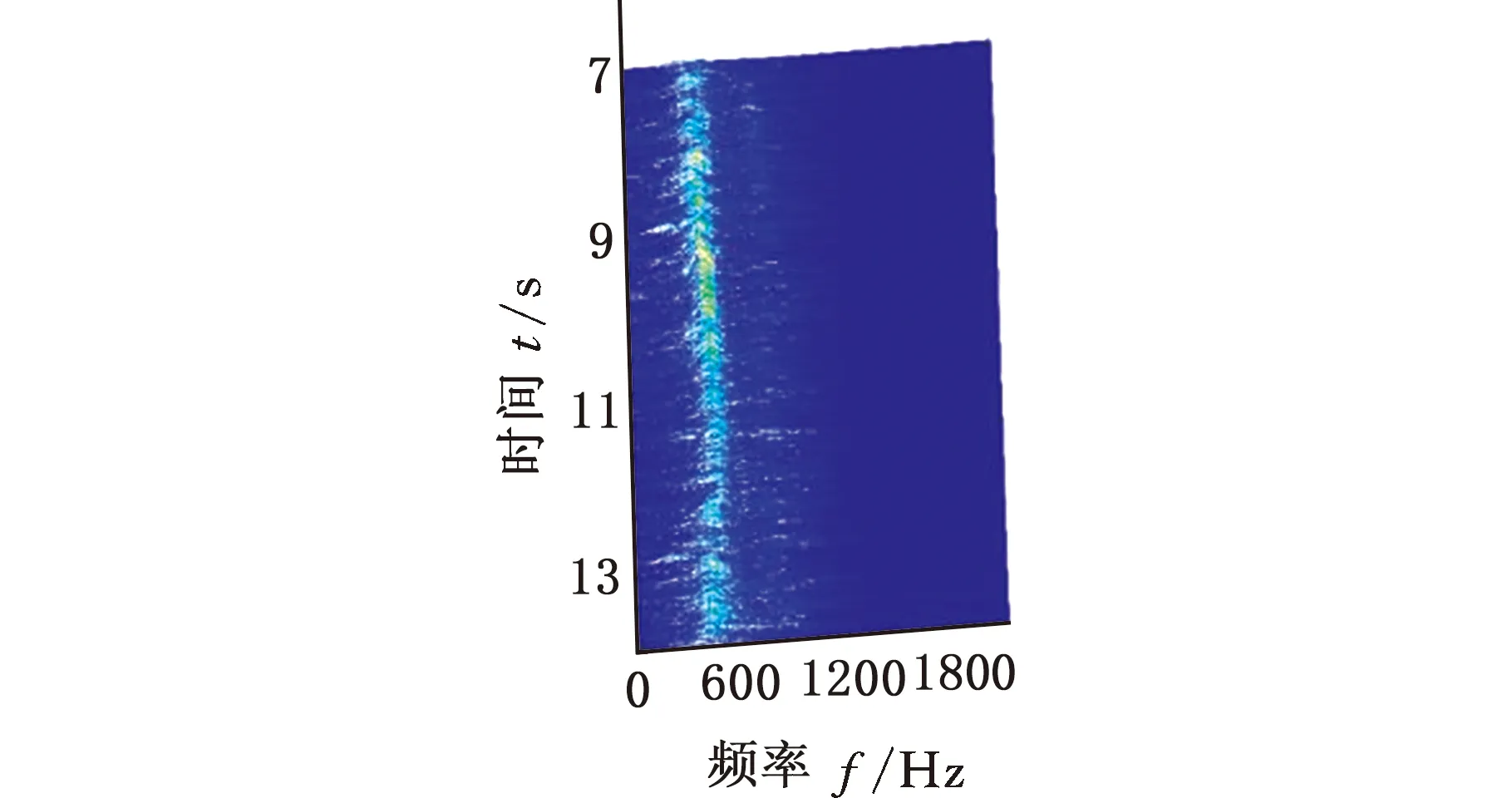
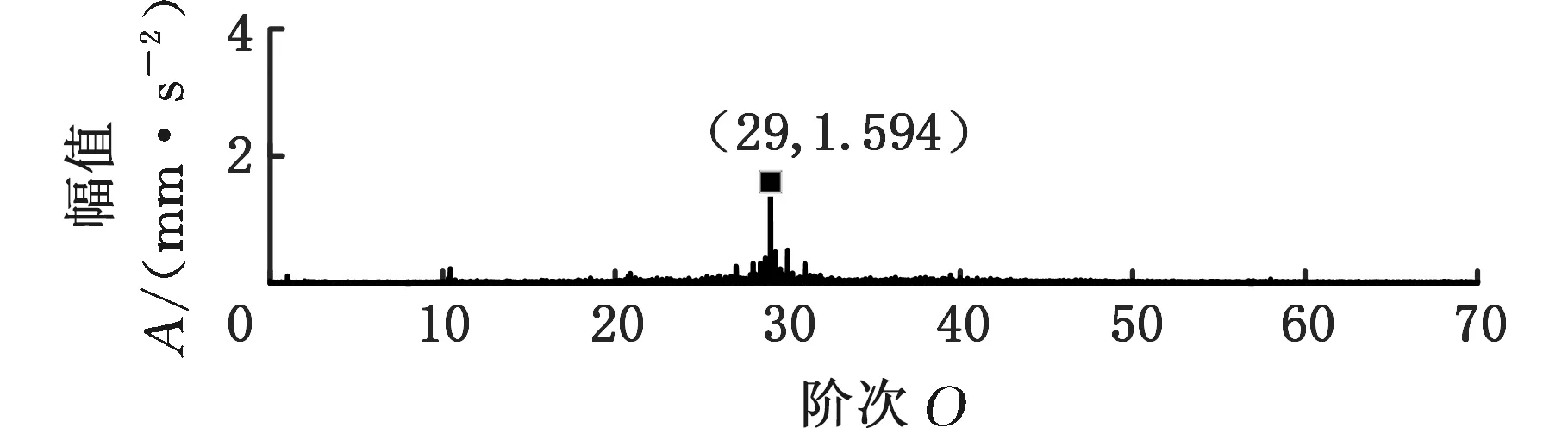
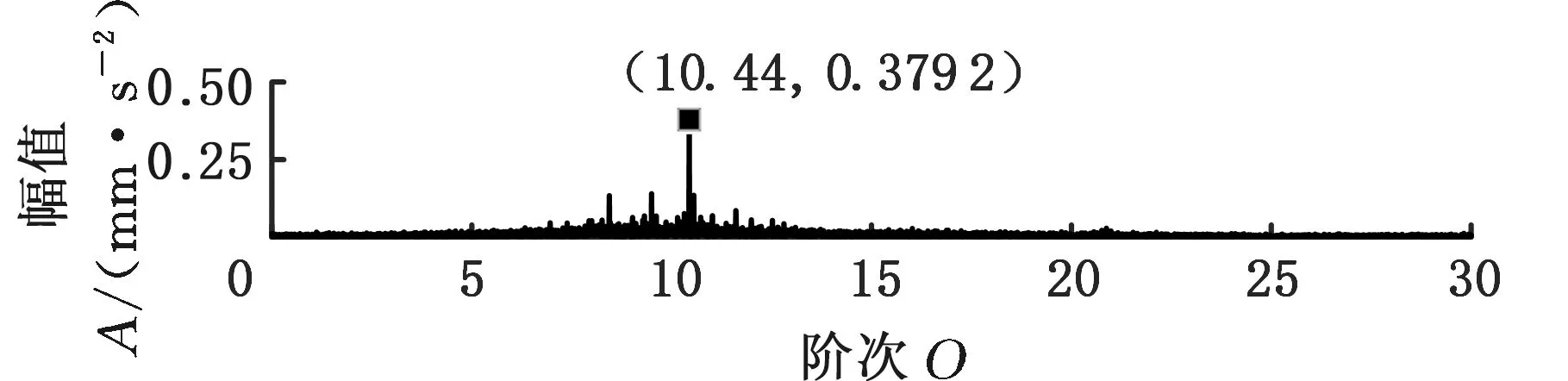
采用MMD方法进行处理,根据时频图的分布情况,预设分量数P=5 (a)某通道信号STFT时频图 (b)分量1 STFT时频图 (c)分量2 STFT时频图图10 变转速工况齿轮箱振动信号(实验1)的MMD分解结果Fig.10 MMD decomposition results of variable rotatingspeed condition gearbox vibration signal(experiment 1) (a)分量1阶次谱 (b)分量2阶次谱图11 分量1和分量2的阶次谱Fig.11 Order spectrum of the first component andthe second component (a)分量1包络阶次谱 (b)分量2包络阶次谱图12 分量1和分量2的Hilbert包络阶次谱Fig.12 The Hilbert envelope order spectrum of the firstcomponent and the second component 对分量1和2进行阶次谱分析,结果如图11所示,两对齿轮副的理论啮合阶次分别为O1=29和O2=10.44。由图11a可以看出,在阶次29.02、58.04处有清晰的谱线,对应齿轮1和2的一倍和二倍啮合阶次,并且在其两边有不对称的调制边频带;由图11b可以看出,在阶次10.45、20.89处有清晰的谱线,对应齿轮3和4的一倍和二倍啮合阶次,同样在其两旁有不对称的调制边频带。为判断边频特征,对分量1和2的Hilbert包络信号进行阶次分析,结果如图12所示。可以看出,图12a中在阶次0.9988处有明显峰值;图12b中在阶次0.2912处有明显峰值,分别对应了转轴Ⅰ和转轴Ⅱ的转频阶次,这说明齿轮啮合振动成分被转频调制,符合齿轮出现局部故障时的故障机理,验证了MMD方法结合阶次分析可有效提取变转速工况下的齿轮故障特征。 (a)IMF1 STFT时频图 (b)IMF2 STFT时频图 (c)IMF3 STFT时频图图13 变转速工况齿轮箱振动信号的EMD分解结果Fig.13 EMD decomposition results of variable rotatingspeed condition gearbox vibration signal 为了对比,采用EMD方法对图9所示信号进行分解,得到的前3个IMF分量如图13所示,为了直观比较,同样采用STFT时频表示。可以看出,由于转速变化,时间尺度跨度大,导致两个啮合振动分量的不同部分被分解到了3个分量之中,失去了原有的物理意义,并且啮合振动分量与重叠的固有振动成分也未完全分离,同时还存在较为严重的背景噪声。对3个IMF分量及其包络信号进行阶次谱分析,结果如图14和图15所示。在图14中虽然存在啮合阶次,但由于受到其他成分和噪声的干扰,表现不明显;而在图15中与转频调制相关的特征阶次也不明显,尤其是转轴Ⅱ的转频阶次。通过对比说明了MMD方法的优势。 (a)IMF1阶次谱 (b)IMF2阶次谱 (c)IMF3阶次谱图14 前3个IMF分量的阶次谱Fig.14 Order spectrum of the first threeIMF components (a)IMF1包络次谱 (b)IMF2包络次谱 (c)IMF3包络次谱图15 前3个IMF分量的Hilbert包络阶次谱Fig.15 The Hilbert envelope order spectrum of thefirst three IMF components 将断齿齿轮3换成同型号正常齿轮进行实验(实验2),实验工况与分析方式同前。原始信号及分解得到的分量1和2如图16所示,可以看出,MMD清晰地分解出了两个啮合振动分量,分解效果良好。分量1和2及其包络信号的阶次谱如图17和图18所示,可以看出,在阶次谱中齿轮1和2的啮合阶次两旁有明显的边频带,而齿轮3和4的啮合阶次旁边频带不明显;在包络阶次谱中主要存在转轴Ⅰ的转频及其倍频阶次,而转轴Ⅱ的转频阶次不明显,这符合齿轮箱实际状况,进一步说明了MMD方法的有效性。 (a)IMF1 STFT时频图 (b)IMF2 STFT时频图 (c)IMF3 STFT时频图图16 变转速工况齿轮箱振动信号(实验2)的MMD分解结果Fig.16 MMD decomposition results of variable rotatingspeed condition gearbox vibration signal(experiment 2) (a)分量1阶次谱 (b)分量2阶次谱图17 分量1和分量2的阶次谱Fig.17 Order spectrum of the first component and thesecond component (a)分量1包络阶次谱 (b)分量2包络阶次谱图18 分量1和分量2的Hilbert包络阶次谱Fig.18 The Hilbert envelope order spectrum of thefirstcomponentand the second component 本文将一种全新的多通道多分量分解(MMD)方法引入变转速工况齿轮故障特征提取,在采用对数窗能量准则提高时频聚集性度量准确性与效率的基础上,将MMD方法应用于具有复杂时频特征的齿轮箱振动信号分析,得到了以下结论: (1)对数窗能量准则能自适应地确定不同采样率下的最佳窗长,融入了对数窗能量准则的MMD方法可减少算法迭代次数和计算时间,为实际振动信号分析提供参考。 (2)通过仿真信号的分析表明,相比于经典的EMD和VMD方法,MMD方法对时间尺度跨度大且时间尺度有重叠的复杂信号具有明显分解优势。 (3)通过对变转速工况齿轮箱振动信号的分析表明,MMD方法可从时频分布复杂的振动信号中有效分解出含有故障特征的分量成分,为齿轮故障特征提取提供了新的有效途径。 另外值得说明的是,MMD方法是基于多通道数据的,但在某些实际工程设备的齿轮箱上安装多个振动传感器可能会受到限制。对于此种情况:一是因为信号之间只要存在相位差,MMD方法就会认为其是不同通道的信号,而实际情况下不同传感器或同一传感器不同方向测得的信号都存在相位差,因此在安装受限的条件下,可以考虑将不同传感器尽可能地紧邻布置在可安装的部位;二是虽然实际振动信号可能包含的分量较多,但包含故障特征的分量一般为前几阶分量,即只要分解出前几个主要分量即可,因此大部分情况下所需的传感器数量不多;三是对于极端情况,如果条件允许,可以尝试在齿轮箱上增加一个放置传感器的装置;反之,可以尝试对采集的单通道振动数据人为设置相位差,从而变为多通道的数据,这是基于虽然相位不同,但其中的分量成分的频率特征不会发生改变,即不会对故障特征提取造成影响,这也是后续的研究方向之一。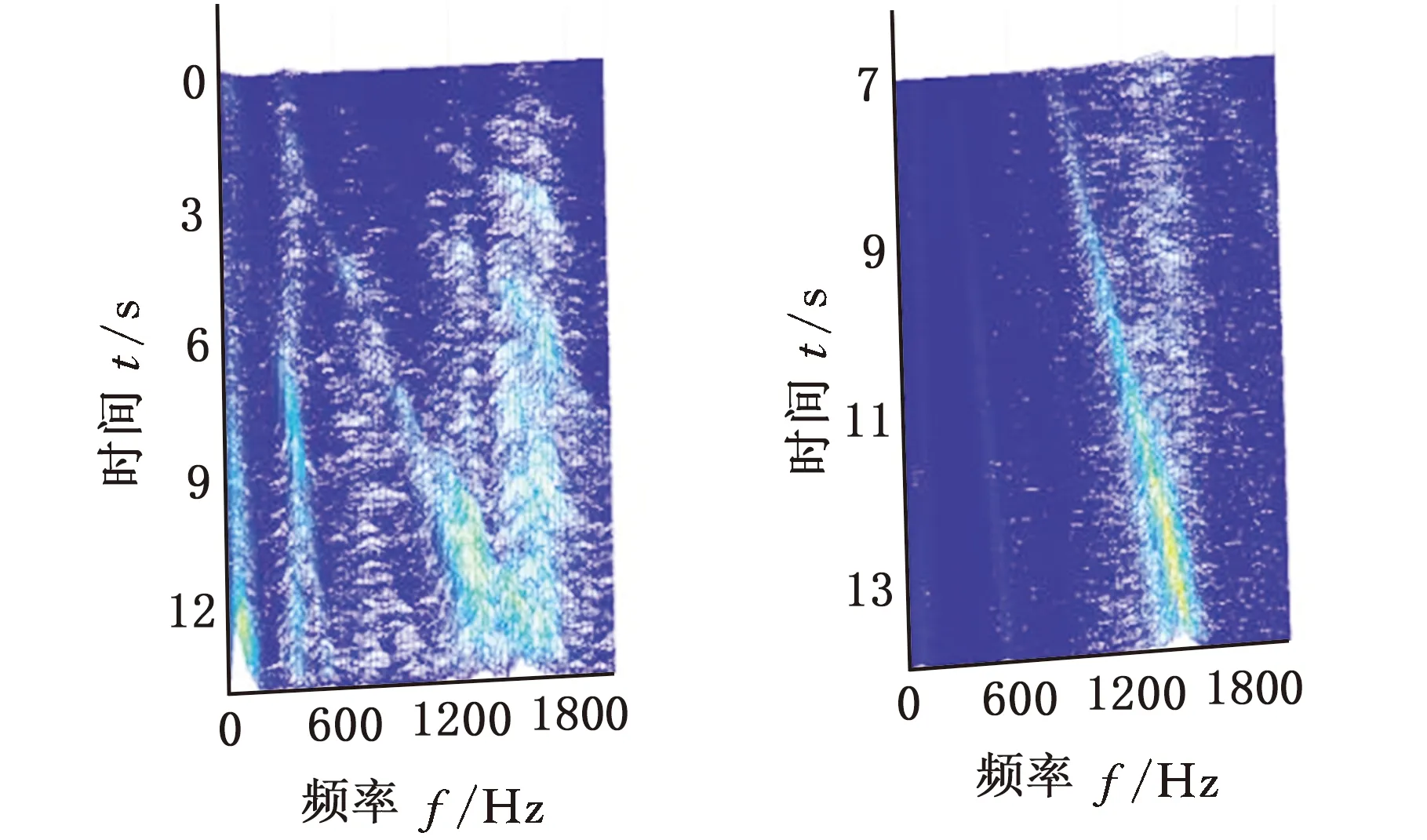

4 结论