软磁复合材料球形感应电机定子磁场分析

李 斌，王思思，郝亚赛，李洪凤

（天津大学电气自动化与信息工程学院，天津 300072）

随着现代航天、军事、化工、工业自动化和智能机器人等领域的发展，对多自由度运动的需求越来越多[1]．常规电机只能产生单自由度运动，需将多个电机以串联、并联或串并混联等方式来产生多自由度运动[2-4]．球形电机可在一个关节实现三自由度旋转运动，有体积小、响应速度快、工作空间非奇异等优点，成为消除传统多自由度装置缺点的一种有效解决方案，在过去几十年中成为国内外学者广泛研究的课 题[5]．相比永磁球形电机，球形感应电机转子结构更加简单，且均匀球体各方向转动惯量相同，有助于减小多自由度运动时的转速波动，减小控制系统设计 难度．

文献[6]设计了一种两自由度球形感应电机，分别由两个方向上的励磁绕组驱动转子在各方向上的转动．文献[7-8]设计了一种单自由度磁悬浮球型电机，在z轴方向通过线圈与转子之间的吸力保持悬浮力控制，在O-xy平面通过两套绕组控制转子运动．文献[9]中的球形感应电机仅有两组定子线圈，转子镀铜，其优点在于线圈数量少，控制简单，缺点在于输出转矩小，应用范围有限．文献[10-11]的电机转子采用表面镀铜空心铁球壳，定子由4个相互独立线圈组成，能够在转子表面产生推力，使得球形转子转动．文献[12-13]设计的壳状球形感应电机将软磁复合材料运用到电机中，转子球外层为导电材料，内层为软磁复合材料，定子层为软磁复合材料，内层为无槽的定子线圈．文献[14]提出的磁悬浮球形感应电机转子表面有互相垂直的槽，槽内安装相互交错的铝条，内表面镀铝膜，外表面的铝条和内表面的铝膜用铝条连接，定子由硅钢片叠压而成，安装三相绕组来产生悬浮电流与旋转电流，但该电机只能产生一个自由度的转动．文献[15]研制了一种基于球轴承多点支撑的球形感应电机，定子采用两个半圆的定子铁芯组合而成，3组定子绕组两两正交分布，以实现三自由度运动．球形转子采用空心球壳，转子表面镀铜，再镀一层铬以减少镀铜层的损伤．文献[16]利用传递矩阵理论设计了一种新型感应球形电机，构造出扩展的简化直线感应电动机模型(ESLIM)．将传递矩阵理论应用于直线感应电机的各层，得到两个边界处磁场的关系，给出了边界条件，推导了磁场的解析模型．

本文提出一种定子轭、定子齿及转子采用SMC材料的球形感应电机结构并对其磁场进行分析，利用定子线圈排布方式和电机结构在空间中的对称性，提出用单组线圈产生的磁场经旋转变换合成电机整体磁场的方法；进一步将球形感应电机单组线圈三维磁场简化为单组线圈二维模型，建立了二维模型的等效磁网络模型并求解气隙磁密分布，用三次样条插值法拟合得到等效磁网络模型的磁密曲线，对比单组线圈三维磁场仿真结果，验证了等效磁网络模型的正确性．本文提出的磁场分析方法将三维磁场简化为二维磁场，在满足计算精度的前提下减少磁场计算数据量，提高了磁场计算速度，克服了电机线圈数量多、结构复杂带来的困难．

1 球形感应电机结构

本文提出的电机结构如图1所示．电机的定子轭和转子均为球壳型，圆柱形定子齿和线圈均匀排布在定子轭球壳内．线圈通入交变电流后产生一个旋转磁场，磁场与转子发生相对运动，转子中产生感应电动势．在感应电动势的作用下，转子导体内部产生感应电流并与定子磁场相互作用，产生了电磁转矩，驱动转子随旋转磁场做同向运动．

图1 SMC球形感应电机结构示意Fig.1 Schematic diagram of SMC spherical induction motor

电机共有24个线圈，两个关于球心对称的线圈为一组，共分为12组，从z轴正负半轴俯视各组标号如图2所示．

图2 SMC球形感应电机的定子线圈Fig.2 Stator coils of SMC spherical induction motor

通过控制球形感应电机各组线圈通电电流可以激励出Y32阶次的旋转磁场．

2 球形感应电机二维等效模型建立

2.1 单组线圈球形感应电机模型

在分析球形感应电机定子磁场时，如果直接对整体磁场进行分析，需要考虑通电后齿与齿之间的磁场交链，增加了分析的复杂度．考虑到球形感应电机的结构具有对称性，可通过关于球心对称的单组线圈的磁场合成整个电机的磁场． 单组线圈通电时，其他11组定子齿都为磁场提供了闭合路径，磁场的等效磁路如图3所示．、Rgap和Rroad分别表示通电线圈所在齿的磁阻，不通电线圈所在齿的磁阻，每个齿对应的气隙磁阻及磁通所经磁路的磁阻(包括定子轭和转子)．理想状态下SMC材料磁导率远大于空气磁导率，定子齿的结构相同且气隙均匀，所以每个齿下的气隙磁阻大小近似相同，根据基本的电路分析，图3圆圈部分支路 没有电流流过，两个电压源的效果叠加作用于电路上端的两个黄色电阻，可以认为单组线圈通电时，所产生的磁动势仅作用到对应齿磁路上，其磁场分布不受其余定子齿的影响．

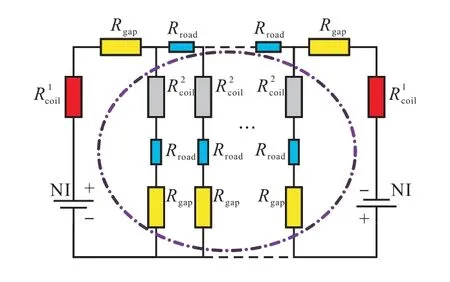
图3 单组线圈通电磁场的等效磁路Fig.3 Equivalent magnetic circuit of the magnetic field of the single-coil group

基于此，可以通过如图4所示的仅含位于z轴正负半轴的单组线圈电机模型代替12组线圈电机模型，从而简化分析，方便磁路解耦．

图4 单组线圈球形感应电机模型Fig.4 Model of the spherical induction motor with the single-coil group

2.2 单组线圈球形感应电机模型二维等效

单组线圈通电后磁场在定子齿、气隙、转子及定子轭之间形成θ＝[0，180°]的闭合磁路，气隙磁密的主要分量为径向分量Br．图5为单组线圈通电产生的Br在球坐标系中的分布．

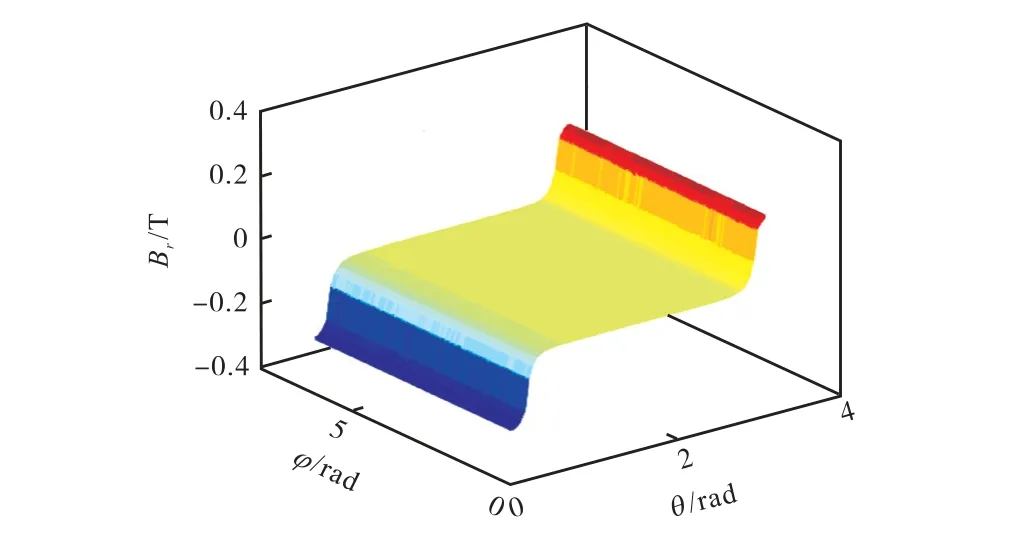
图5 单组线圈通电的Br分布Fig.5 Distribution of Br of the single-coil group

可以看出球形感应电机气隙球面上不同φ值Br在θ＝[0，180°]内的波形相同，可以将单组线圈三维磁场分析简化为任意φ值二维截面的磁场分析，定义二维截面为单组线圈二维模型，如图6所示．其中Dcop为线圈底面直径，Dsmc为SMC定子齿底面直径，Hcop为线圈高度，Rsi为定子轭内半径，ds为定子轭厚度，Rri转子内半径，dr为转子厚度．

图6 单组线圈二维模型示意Fig.6 Schematic diagram of a two-dimensional model of the single-coil group

3 二维模型磁场的等效磁网络法求解

3.1 单组线圈二维模型中线圈的等效

单组线圈二维模型中线圈形状如图7(a)所示， 建模时将线圈的形状等效为扇形，将定子轭内径处的线圈弧长近似等于Dcop，齿的弧长近似等于Dsmc，线圈高度不变，如图7(b)所示．

图7 线圈等效示意Fig.7 Equivalent diagram of the coil

这种等效方法保证了同一个剖分单元中磁阻计算采用同一个相对磁导率，并能根据Rsi计算出每一个剖分单元的圆心角为

3.2 剖分单元磁阻及磁动势推导

对单组线圈二维模型沿径向和周向进行剖分，建立其等效磁网络模型．基于单个节点磁路模型中各个节点之间的连接关系和磁通连续条件，可以将单元方程表示为

式中：φ为支路的磁通量；u为节点磁势；F为支路上的磁动势；R为磁阻；上标φ和r分别表示周向和径向两个方向；下标i和j分别表示对应的节点在二维空间中的位置．

单组线圈二维模型仅采用磁阻元件的周向分量Rφ和径向分量Rr，分别表示为

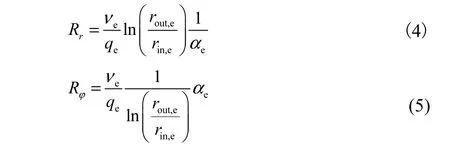
式中：νe为剖分单元的磁阻率；qe为轴向长度，本文取qe＝1 mm；rout,e为剖分单元扇面外径；rin,e为内径；αe为扇面角．

电机的激励源为定子线圈，定义线圈产生的磁动势Fcoil为每个电磁线圈的安匝数NI．假设整个线圈区域电流密度分布均匀，磁动势源增量ΔFe为

式中：Ae为磁阻元件载流区面积；Acoil为线圈在槽中的总面积；Ncoil为线圈数；Na,coil为线圈中并联导体数；比值Neff,coil为线圈中有效导体数，本文中 Neff,coil＝1；Icoil为电流值．磁动势源在SMC定子齿顶部处为0，在线圈区域内随线圈高度线性增长最终达到最大值Fcoil，并且在定子轭中恒等于Fcoil．

3.3 磁通密度求解

利用节点电压分析法求解单组线圈二维等效磁网络模型，将式(2)中的单元方程式应用于所有节点组成式(7)中的系统矩阵，其中P为磁导纳矩阵，u为节点标量磁势矩阵，F为驱动矩阵．

若整个分析区域在径向和周向两个方向上分别剖分成s和t个节点，总节点数n为s和t的乘积，任意节点(i，j)的顺序即n(i，j)可以表示为

任意节点(i，j)的单元方程式属于系统矩阵的第n(i，j)行．属于第n(i，j)行的u、P和F元素表示 如下.

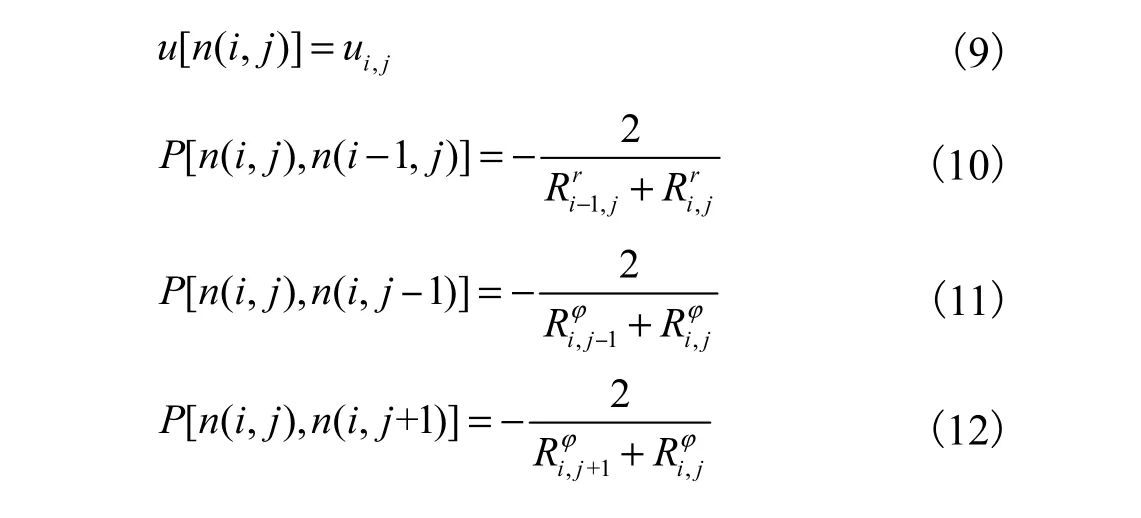
磁能和支路磁通、磁阻的关系可表示为

用三次样条插值的方法对磁密数据进行拟合，得到等效磁网络法求解的r＝31.1 mm气隙处Br随弧长变化曲线如图8所示．

图8 三次样条插值的Br曲线

拟合曲线误差平方和SSE＝0.001682，证明三次样条插值对等效磁网络求得的磁密数据拟合准确．

4 球形感应电机整体磁场合成

单组线圈球形感应电机通单位电流后，气隙磁密径向分量Br表示为不同阶数球谐函数相加的形式为

式中：l∈N表示函数阶数；m∈[0，l]表示函数的次．

假设磁场不饱和，球谐函数的空间旋转可以基于球谐波系数变换进行[17]，基于此能够通过单组线圈通单位电流的气隙磁密获取电机12组不同位置线圈产生的气隙磁密．结合球谐函数形式的单组线圈产生的气隙磁密径向分量表达式，通过空间磁场的叠加定理，可得球形电机某气隙面上各点的磁密径向分量表达式[18]为

式中ik为各组线圈通电电流，k＝1，2，…，12．

5 仿真与实验

5.1 单组线圈球形感应电机有限元仿真

表1给出了球形感应电机的一组尺寸参数．

表1 SMC球形感应电机尺寸参数Tab.1 Size parameters of SMC spherical induction motormm

为说明SMC球形感应电机单组线圈通电时齿与齿之间的磁场交链情况，依据表1建立电机12组线圈仅第1组线圈通电的有限元仿真模型，对比两种情况Br在球坐标系的分布及球谐波系数如图9和10所示．

图9 第1组线圈通电后Br分布对比Fig.9 Comparison of the Br distribution with electrified Group1 coils

情况1为保留第1组定子齿材料为SMC，其余齿材料设为空气；情况2为保留所有定子齿材料为SMC．可以看到两种情况下磁密幅值和球谐波系数组成基本相同，且球谐波系数和的幅值相同．对比了情况1和情况2的球谐波系数中幅值最大的10组数据，如表2所示．

表2 两种情况球谐波系数对比Tab.2 Comparison of SHC in two cases

5.2 有限元仿真结果与等效磁网络对比

依据表1建立单组线圈三维磁场模型和单组线圈二维磁场有限元模型，设置NI＝300 AN，电流产生的磁场指向z轴负方向，获得r＝31.1 mm气隙处磁密径向分量Br在θ＝[0，180°]范围内随弧长ξ变化的幅值图．在等效磁网络模型中设置NI＝300安匝，计算得到Br数据并进行三次样条插值拟合．

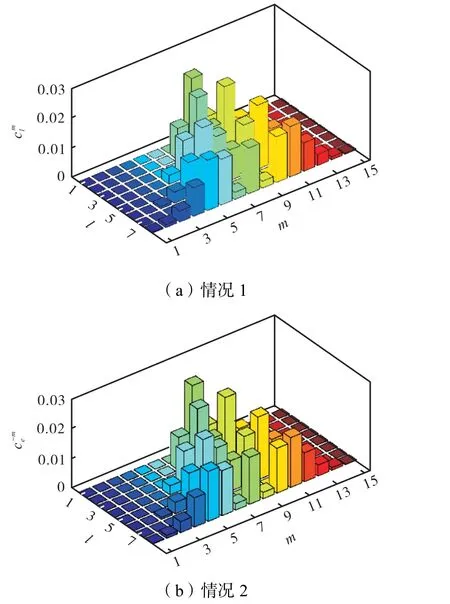
图10 Br的球谐波系数组成对比Fig.10 Comparison of SHC of Br

图11中3条曲线分别代表单组线圈三维磁场模型、单组线圈二维磁场模型和等效磁网络模型在 NI＝300 AN时的Br分布，图11(b)和图11(c)将图11(a)磁密绝对值大于0的A、B两部分进行了放大．

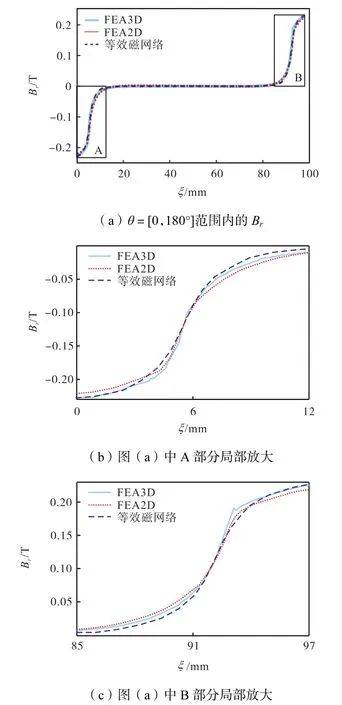
图11 3种模型的Br（NI＝300安匝）Fig.11 Br of the three models（NI＝300 AN）

3条曲线的趋势相同，磁密较大区间内三者相对误差最大不超过4.50%．随着漏磁影响的增强三者相对误差有所增大，在磁密趋近于0时相对误差又逐渐减小．等效磁网络模型同单组线圈三维磁场模型和单组线圈二维磁场模型相对误差的平均值分别为13.34%和18.53%．

5.3 样机磁场测量实验

本次实验选用了Hoganas公司生产的SMC标准件进行样机加工，实验样机尺寸如表3所示．

表3 实验样机尺寸参数Tab.3 Size parameters of experimental prototype mm

实验样机如图12所示．受限于SMC标准件的尺寸和加工工艺，转子由两个半球拼接而成，定子轭由均分的6个单元拼接而成，拼接处做轻微打磨方便绕组穿出，塑料线圈骨架固定绕组于定子齿上，支撑底座起固定并支撑样机的作用．图12(a)未显示顶部定子轭单元以展示样机内部结构．

图12 SMC球形感应电机样机Fig.12 SMC spherical induction motor prototype

5.3.1 静态磁场测量实验

本实验搭建的样机实验平台如图13所示，包括上位机、直流电源、FPGA电路、信号驱动电路、样机、霍尔信号采集电路等模块．上位机完成FPGA程序的编译，FPGA电路采用EP4CE6E22C8N芯片，输出12路电流数字信号分别进入12路信号驱动电路．信号驱动电路包括DA转换、运放电路、功放电路以及电流采样4个模块．电流数字信号经过DAC7571数模转换芯片转化为模拟信号，经运放电路的LM258芯片缩小10倍后再由功放电路芯片LM1875放大，提高电路整体带载能力，设计了滑动变阻器实现时时调节放大倍数的功能，最后经过ASC712-05B电流传感器芯片后加载到样机12组线圈上．霍尔信号采集电路采用AH49H线性霍尔，用来采集霍尔元件输出的电压信号，结合霍尔元件磁场 计算公式获得磁场数据．

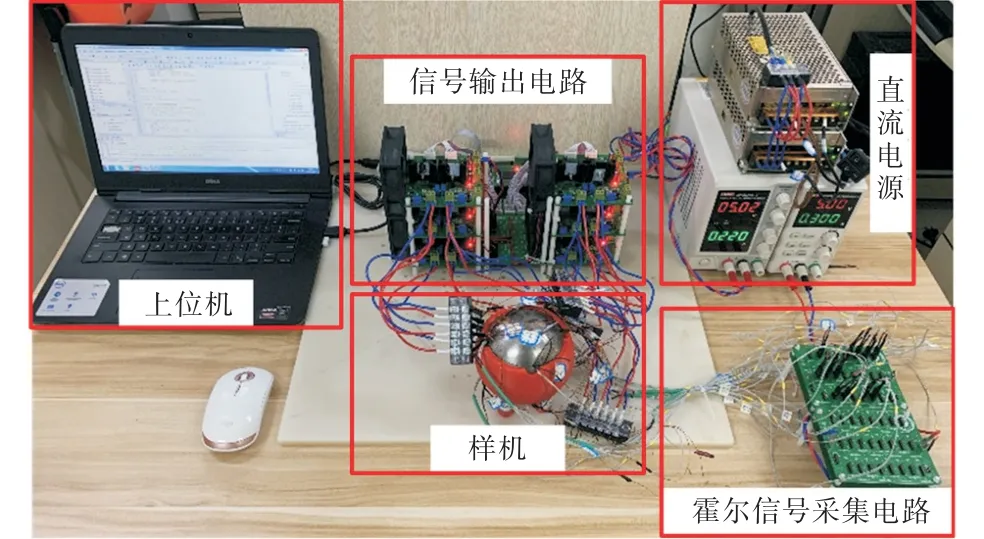
图13 实验平台Fig.13 Experimental platform

首先测量了样机在单组线圈通静态电流时r＝31.1 mm处的气隙磁场．选择了位于z轴正负半轴上的2号和-2号线圈，在两线圈间θ＝[0，180°]的弧线上贴满霍尔元件，每个霍尔元件的测量平面与定子线圈底面相切，使其可以测得定子线圈激励出的径向磁密，同时确保霍尔元件中心处于r＝31.1 mm的球面上，如图14(a)所示．

图14 霍尔元件位置Fig.14 Location of the Hall components

实验中线圈实际匝数为105匝．在2号和-2号线圈中通入产生磁场指向z轴负方向的直流电，得到NI＝210 AN时r＝31.1 mm处气隙静态磁场径向分量Br，并对比NI＝210 AN时等效磁网络模型和有限元仿真的电机单组线圈静态磁场Br．

图15为NI＝210 AN时实验样机单组线圈通电、单组线圈三维磁场有限元仿真和二维等效磁网络模型得到的Br在θ＝[0，180°]内的曲线，3条曲线的趋势相同，且由于实验样机定子轭上不可避免地存在部分气隙，使得实验值较其他两组数值的幅值偏小．

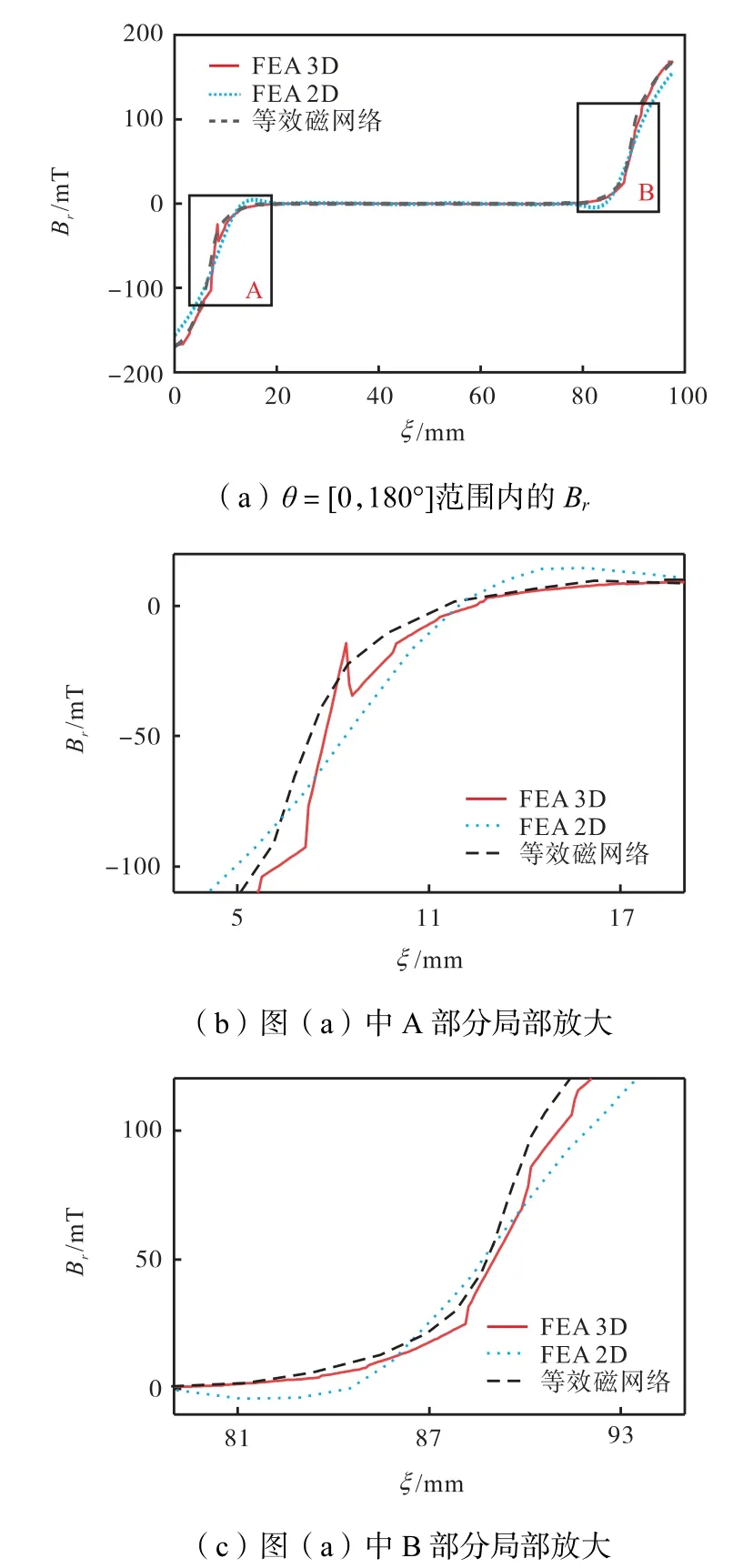
图15 NI＝210 AN静磁场实验的Br对比Fig.15 Comparison of Br in the static experiment when NI＝210 AN

计算了NI＝210 AN时实验同其他两组数值间的相对误差．实验与等效磁网络模型的平均相对误差为18.44%，实验与有限元仿真的平均相对误差为15.14%．误差来源主要为样机存在的气隙、霍尔元件测量灵敏度以及霍尔元件表贴位置的偏差．

5.3.2 整体磁场测量实验

本实验测量了球形感应电机12组线圈依据通电策略通电后r＝31.1 mm处的整体磁场，每个线圈底面圆心处表贴一个霍尔元件，共24个霍尔元件，如图14(b)所示(未显示顶部定子轭单元)．

选择Y32型磁场沿z轴旋转的运动轨迹，电流频率f＝500 Hz，通过分相通电策略[19]计算出12组线圈电流的表达式为

实验选取了6 ms和7 ms时12组电流的瞬时值通入电机线圈，得到样机依据通电策略通电后两个时刻下的磁场数据．同时利用有限元仿真得到电机通入12组电流后的气隙磁场径向分量Br．

对实验得到的Br数据进行可视化处理，如图16和图17所示．将t＝6 ms和t＝7 ms时上半球各线圈的霍尔元件检测磁场在对应时刻的Y32磁场分布图中标出，可以看出测量磁场的幅值和分布与Y32旋转磁场一致．

图16 上半球12个线圈检测磁场的幅值与分布（t＝6 ms）Fig.16 Amplitude and distribution of the magnetic field of 12 coils in the upper hemisphere（t＝6 ms）

图17 上半球12个线圈检测磁场的幅值与分布（t＝7 ms）Fig.17 Amplitude and distribution of the magnetic field of 12 coils in the upper hemisphere（t＝7 ms）

6 结 语

本文以SMC材料球形感应电机为研究对象，对其磁场分析方法进行了研究，通过分析电机单组线圈通电的磁场特性引出单组线圈球形电机模型，基于球谐函数的旋转变换简化了球形感应电机整体磁场计算；提出将单组线圈球形电机三维磁场模型简化为二维模型的磁场分析方法，建立其等效磁网络模型，推导了剖分单元的磁阻及磁动势表达式并计算得到磁网络模型气隙磁密分布；通过对比单组线圈球形感应电机三维磁场和单组线圈二维模型的有限元仿真，结合样机静态磁场测量实验结果证明了等效磁网络模型的正确性，说明本文提出的SMC材料球形感应电机磁场分析方法具有实用价值．该方法对其他铁磁材料球形电机的分析工作具有参考意义，同时为转矩分析和控制策略的研究奠定基础．