基于学习和模型相结合的光场超分辨率方法

杨敬钰，曾昕阳，卢 志，金满昌，岳焕景

（1. 天津大学电气自动化与信息工程学院，天津 300072；2. 清华大学自动化系，北京100084）

光场成像的雏形可以追溯到1903年Ives发明的双目视差显示系统中运用的针孔成像技术．1936年，Gershun提出光场的概念，将其定义为光辐射在空间各个位置向各个方向的传播[1]．随着全息理论的提出和微透镜阵列成像技术、计算机技术的不断发展，2006年，Levoy等[2]将光场渲染理论运用于显微成像，并研制出光场显微镜(light field microscopy，LFM) ．光场显微镜是通过在传统光学显微镜的中继像面上插入一块能够捕获光场信息的微透镜阵列来实现的，它可以记录来自不同空间位置和不同视角的光信息．光场图像通过4D光场数据的反演可重建多视角图像和多层焦平面图像，利用反卷积算法和断层重建可实现三维显微成像．由于这些后续处理可以通过一次曝光实现，因此光场显微镜对观察运动的活体微生物和光敏感样品有其独特优势，广泛应用于光学成像、立体光照(volumetric illumination)、3D分割等领域．

光场成像过程存在角度域和空间域之间分辨率权衡的基本问题[3-4]．由于受到光场成像设备物理属性的限制，光场显微镜通过牺牲空间分辨率来提高角度分辨率．因此，有限的空间分辨率给相关应用的发展带来了困难，成为光场成像的主要瓶颈[5]．如何提高光场图像的空间分辨率，成为光场领域的重要研究内容．文献[6-8]基于各种优化框架得到分辨率较高的光场图像．但是，在一定的扫描速率下，这种方式将大大增加成像的时间，不利于快速实时成像．因此，光场图像超分辨率(light field super-resolution，LFSR)需要一种高精度、高速度的实现方案[9]．

目前光场图像超分辨率方法主要是基于卷积神经网络(convolutional neural network，CNN)实现的[10]. 但它们中的大多数依赖通用的卷积神经网络架构，这些架构没有明确地考虑物理模型．本文受到图像正则化方法[11]、迭代优化理论[12]和深度学习[13]技术的启发，提出了一种基于深度学习和LADMM算法结合的光场图像超分辨率方法．它是一个可训练的超分辨率网络，与其他数据驱动方法相比，具有物理意义上的可解释性．本文首先介绍几种常见的LFSR方法，然后给出本文采用的LFSR模型和传统的LADMM算法，最后详细介绍本文提出的基于学习和模型方法相结合的光场超分辨率网络模型．基于斑马鱼数据集的实验结果表明，本文提出的光场图像超分辨率方法在给定条件下具有较好的图像超分辨率处理能力，并且带有一定的去噪功能．果蝇光场数据集的实验结果证明了本文的方法相比传统LADMM算法在性能和效率上更具优势．

1 相关工作

根据光场记录空间信息和角度信息的特性，LFSR可以看作一种特殊的图像超分辨率，特殊之处在于其不同角度的图像之间具有相关性．近年来，一些研究者提出了利用光场图像角度相关性的SR方法[4,10,14-15]，然而Cheng等[5]研究发现不使用任何角度信息的单一图像超分辨率(single image superresolution，SISR)方法仍然优于其他许多LFSR方法．考虑到基于深度学习的单一图像超分辨率在技术上足够成熟，而且利用角度信息需要额外的处理过程，本文使用SISR作为LFSR的方法，不考虑不同角度之间的相关性．

根据图像降质模型，LFM的高分辨率(high resolution，HR)图像和低分辨率(low resolution，LR)图像之间存在确定的关系，即每一幅LR图像都是对应的HR图像在亚像素水平上的一个子采样．因此，LFSR可以看作是一个不适定(ill-posed)反问题[16]．目前有两种主流的方法解决反问题，一种是基于模型(优化)的方法，另一种是基于学习的方法．

1.1 基于模型(优化)的光场图像超分辨率

解决反问题的一个重要方法是基于模型(优化)的LFSR[5,10]．基于模型的LFSR利用图像先验、Total Variation(TV)等相关正则化方法和优化算法，基于明确的物理解释和数学推导，取得了良好的效果[8,17-21]. 一些优化算法在多个领域都取得不错的表现，如ISTA[17,21]和ADMM[18-20]．然而，这些方法大多利用了一定的结构稀疏性作为图像先验，并采用迭代方式解决稀疏性正则化优化问题，因此在硬件上重建图像的计算复杂度较高[22]．另外，图像先验的选择和模 型参数调整的成本较高，使得该方法难以获得优良 结果.

1.2 基于学习的光场图像超分辨率

随着深度学习的广泛使用，基于学习的LFSR成为解决反问题的一个重要方法．近年来，随着卷积神经网络和生成对抗网络(generative adversarial network，GAN)等[23]基本结构的提出，产生了很多有影响 力 的 网 络(如：ResNet[24]、DenseNet[25]、SRCNN[26])，在基于学习的LFSR方面的研究取得了令人瞩目的成就[10,15,27-28]．在LFSR中引入深度学习，利用多通道SRCNN体系结构可以实现光场的空间和角度超分辨率，在此基础上，Fan等[15]设计一个两级CNN网络，分别利用光场的外部和内部的相关性，首次在patch级别融合不同的角度，以补偿LFSR的视差．而Wang等[28]改进循环卷积实现对相邻角度之间的空间相关性进行建模，将水平子网络和垂直子网络集成为最终输出．与基于模型的LFSR不同，基于学习的LFSR将LR和HR图像之间的关系建模为一个适当的映射，网络中的参数经过训练自动更 新[5]，显著降低了时间复杂度[22]．

1.3 基于模型方法和基于学习方法之间的关系

一些研究探索了基于模型的方法和基于学习的方法之间的关系[22,29-30]．Gregor等[29]探索了共享的分层神经网络和ISTA算法[31]之间的相似性，并将后者展开为深度网络．Li等[30]指出具有相同线性变换的前馈神经网络在不同层间的传播等效于使用梯度下降算法最小化某个函数．ADMM存在一组可学习参数来生成全局收敛的解，可以通过适当的方式进行训练．这些理论分析有效地弥合了两种方法之间的差距．在具体实践中，针对图像去噪、去马赛克、自然图像超分辨率和压缩感知(compressed sensing)等问题，研究人员提出了一些基于模型和基于学习的方法相结合的方案[22]．这些工作表明，将基于模型方法和基于学习的方法结合可以综合两种方法的优点．然而，目前还没有研究应用这种组合方法来解决LFSR问题．笔者认为，本文提出的基于学习和模型相结合的光场超分辨率方法是一种崭新的LFSR问题实现方案，可以提高结果的性能．

基于以上思路，本文将数据驱动结构与经典的优化算法相结合，提出了一种基于模型和基于学习结合的LFSR方法．具体来说，本文提出了一种新的深度网络模型，称为LAC-LFSRnet(LADMM-CNN for light field super resolution)，启发自线性交替方向乘子法(LADMM)[32]，用于求解LFSR模型的L2平方范数正则化问题，将迭代优化求解模型转化为深度展开网络(deep unfolding network)．LAC-LFSRnet的主要部分由固定数量的层(或阶段)组成，每个层(或阶段)反映了类似于LADMM算法迭代的特征．与传统的LADMM算法不同，LAC-LFSRnet中涉及的所有参数(如先验、拉格朗日乘子、惩罚因子等)，在训练端到端网络时使用损失函数最小化，并在反向传播时进行更新．此外，网络中带有残差的CNN块进一步增强了网络的表达能力，改善了超分辨率结果．

总之，LADMM算法参数的可学习化与残差网络结合，使LAC-LFSRnet同时具有基于模型的LFSR和基于学习的LFSR的优点，即具有定义良好解释的高精度LFSR．基于真实斑马鱼数据集的实验表明，所提出的LAC-LFSRnet能够很好地完成超分辨率的任务．由于本文的网络具有比较深的层数，与以往的方法相比，它具有一定的处理联合超分辨率和去噪任务的能力．本文基于果蝇数据集的实验证明了本文提出的网络在超分辨率性能和运行时间上都要明显优于传统LADMM算法．

2 方 法

本节将首先建立LFSR模型并介绍传统的LADMM优化算法，然后详细介绍本文设计的LACLFSRnet网络结构．

2.1 LFSR模型和传统LADMM算法

根据文献[33]定义，本文定义光场为M ×M个微透镜阵列的输出，其中每个微透镜阵列装备N ×N像素传感器，因此光场可以表示成一个N ×N ×M ×M尺寸的张量U (x ,y ,s, t )，其中(x, y)是空间坐标，(s ,t)是角坐标．LFSR问题可以描述为如何从低分辨率光场图像V恢复到高分辨率光场图像U (x ,y ,s, t )．本文定义超分辨率因子α∈N，则V的分辨率为N/α× N/α×M ×M．本文的目标是，对给定的每个角度的低分辨率图像V (·,·, s, t)∈R(N/α)×(N/α)，重建高分辨率图像U (·,·, s ,t )∈RN×N．本文设U (·,·,s, t )和V(·,·,s, t)的向量形式分别为u ∈RN2，v ∈R(N/α)2，则对应的一组高分辨率图像HR和低分辨率图像LR的关系可用式(1)表示．

式中：S ∈R(N/α)2×N2表示下采样矩阵；n ∈RN2表示噪声．这是一个典型的不适定问题，LFSR模型(式(1))可以表示为一个凸优化问题．

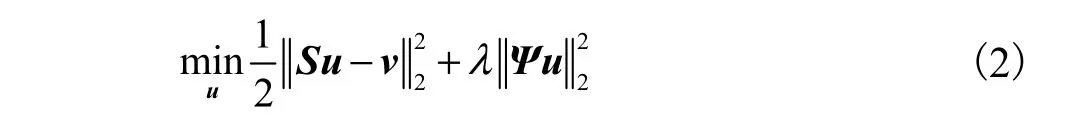
式中Ψ是变换矩阵(如小波变换)．在式(2)中，第1项代表数据项，第2项为具有L2平方范数的向量Ψu的正则项．式(2)中，基于交替方向乘子法思想，将优化变量拆分为两个不同的变量u和z，那么增广拉格朗日函数(augmented Lagrangian function)可以表示为

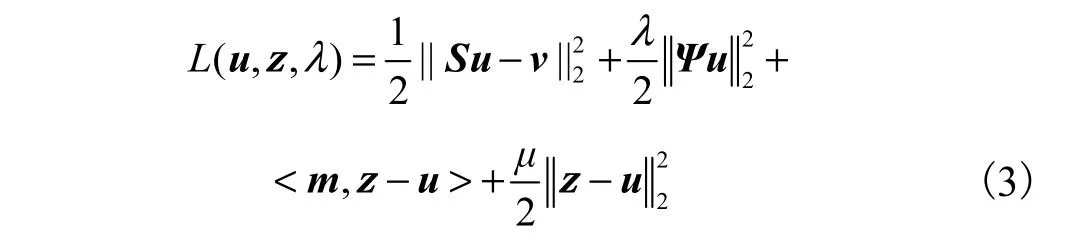
式中：m是拉格朗日乘子；μ是惩罚因子．使用传统LADMM优化算法，式(3)可以使用以下步骤迭代 更新．

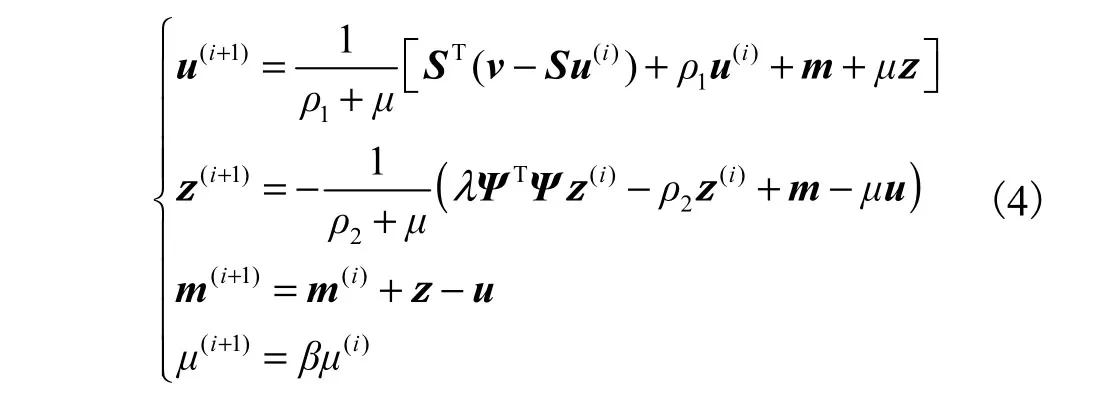
式中：i表示LADMM的迭代次数；β为步长；ρ1、ρ2为线性化系数．

2.2 LAC-LFSRnet

传统的ADMM/LADMM优化算法通常需要数十次甚至上百次迭代才能获得满意的结果．此外，算法中有众多参数(如β、λ、ρ1等)和变换矩阵Ψ需要手工指定．因此，本文在传统LADMM的启发下设计了LAC-LFSRnet网络，以克服上述传统LADMM存在的缺点．该网络结构的基本思想是结合LADMM和深度神经网络的优点，对LADMM的迭代算法转化为一个深度展开网络．

本文的LAC-LFSRnet可以分为两部分，即主体部分和后处理部分．LAC-LFSRnet的主体部分包含多个网络层，每个网络层都对应传统LADMM算法中每次迭代更新步骤的表达式．除式(4)中的更新规则外，在每一层添加一个带有残差的CNN块，称为细化模块，以增强网络表达能力，提高结果的性能．整个结构尾部的LAC-LFSRnet后处理部分合并主体各层的结果，以充分利用之前学习到的信息．本文接下来讨论LAC-LFSRnet的细节．

2.2.1 LAC-LFSRnet主体部分

图1(a)给出了LAC-LFSRnet的整体网络结构，包含主体部分和后处理部分．主体部分的一层可分为两个模块，即LADMM模块(如图1(b)所示)和细化模块(如图1(d)所示)．例如对于变量m，本文指定第i＋1层的输入为 m(i)，输出为 m(i+1)．为了清楚地描述网络机制，本文以LAC-LFSRnet的第i＋1层为例进行介绍．

1)LADMM模块

LADMM模块的第i＋1层对应式(4)，变量u、z、m、μ由上一层迭代更新得到．具体分析如下. ①当u(i)更新为u˜(i)时，LR图像v和下采样矩阵S给定，ρ1设置为可学习的参数，而不再是算法中的固定值．另外，考虑到 STv项可能会产生额外的规则分布伪影，本模块用可学习的η参数与该项相乘来避免这种情况．②当z(i)更新为z(i+1)时，λ和ρ2是可学习的参数．已有文献[22]表明，当卷积过滤器是线性的且具有矩阵形式时，变换Ψ可以表示为Ψ z=AR elu(Bz)形式，其中A和B是卷积核．同理对于 ΨT也可以进行类似的表示．因此，本文使用一个对称的基于CNN的子模块(如图1(c)所示)替换ΨTΨ z项，其中第1个和最后一个卷积核用来变换特征图的数量，剩下的对称部分表示变换 ΨTΨ．③当m(i)更新为 m(i+1)时，根据式(4)，容易由z、u得到．④当更新µ(i)时，步长β是可学习参数．总之，在LADMM模块中的可学习变量集Θ包含{ρ1, ρ2,η,λ, ΨTΨ ,β}(Li)，其中L是LAC-LFSRnet的总层数，i= {1 ,2,…,L}是层号．考虑到 ΨTΨ(i)子模块中需要卷积处理，所以本网络使用矩阵形式而不是向量形式实现网络，以避免在向量形式和矩阵形式之间反复转换．

在LADMM模块中，4个迭代变量进入第1层网络时的初始值为：z(0)=0，u(0)=0，m(0)=0，µ(0)=0.005．

2)细化模块

2.2.2 LAC-LFSRnet后处理部分

如图1(a)所示，LAC-LFSRnet的后处理部分用于处理主体部分每层i = 1,2,…,L的结果．后处理部分由分层混合模块和尾部细化模块组成，最后输出超分辨率的结果u(i)．

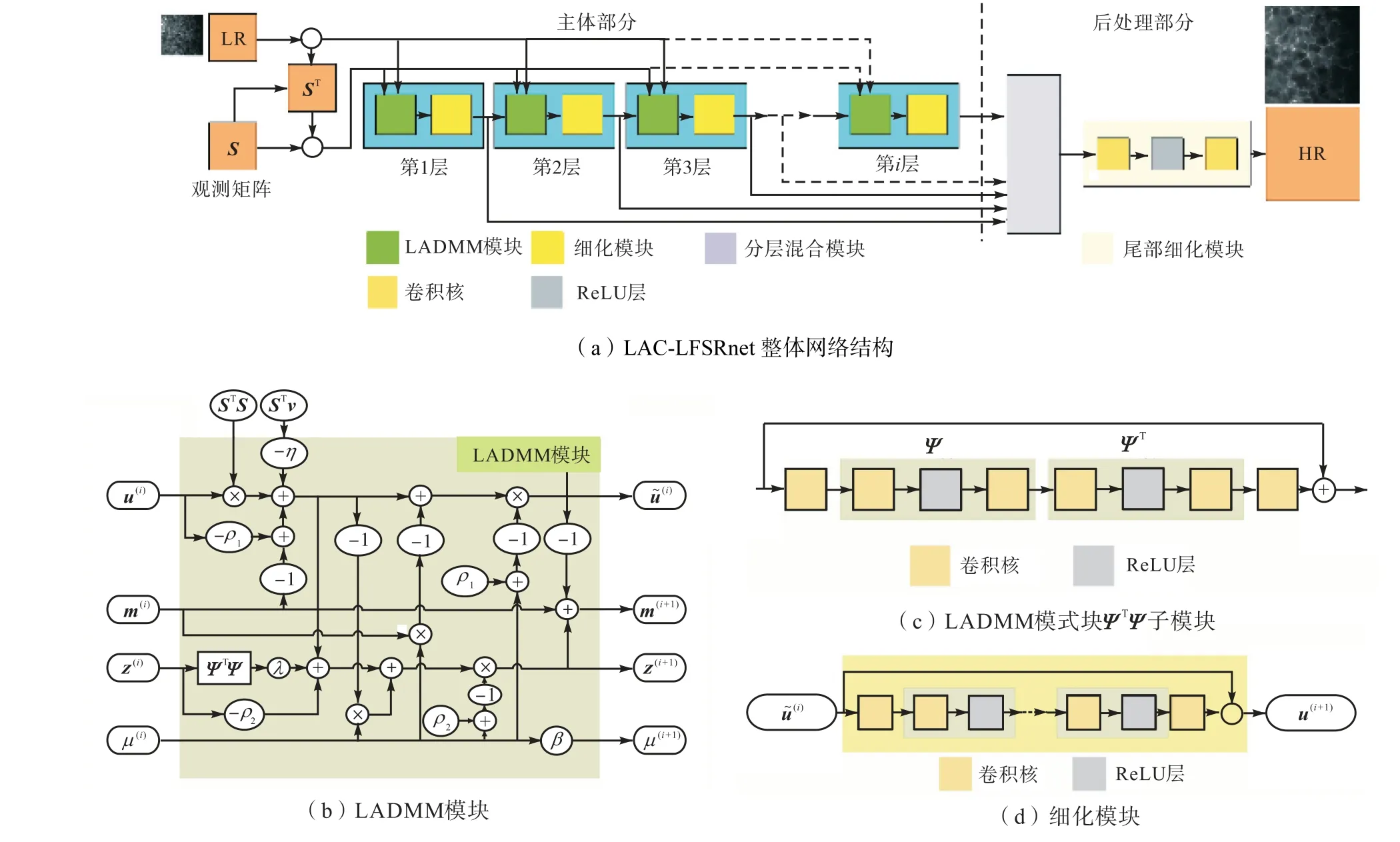
图1 LAC-LFSRnet网络结构Fig.1 Structures of the proposed LAC-LFSRnet network

1)分层混合模块

分层混合结构是一种被证实有效的结构，用来融合不同的特征图[34]．从迭代优化的角度而言，网络每一层的输出u(1)，u(2),…, u(L)对应每次迭代的结果．在Xie等[35]的工作中，每层u(i)(i = 1,2,…,L)分别与HR图像进行比较计算损失函数 loss(i)(i = 1,2,…,L)，总损失是所有 loss(i)的简单求和．然而，每层网络的输出对结果的贡献可能并不相同，即某些层输出的结果可能包含了更多有用的信息，这些层的输出相对其他层应该具有更高的权重．为使不同层的输出具有自适应的权重，本文应用一个1×1卷积核的瓶颈层(bottleneck layer)，可以表示为

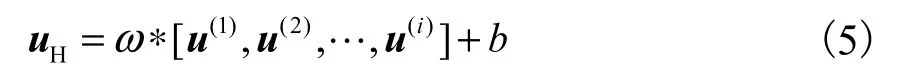
式中：*表示卷积操作；[u(1), u(2),…, u(i)]表示网络每层的输出在通道维度上的拼接操作；b为偏置．

2)尾部细化模块

它位于整个LAC-LFSRnet网络的尾部，由卷积层和ReLU层组成．卷积层的作用是减小分层混合模块的输出uH的通道数，ReLU层增强了最终输出的非线性表达能力，避免反向传播过程中梯度消失．实验结果表明，由主体部分和后处理部分组成的LACLFSRnet的性能优于只有主体部分的LFSRnet．

3 实验结果与分析

3.1 数据准备

本文使用斑马鱼光场数据集产生训练数据对{ y(0),u}，其中y(0)表示网络的输入，u为真值．在真实光场成像过程中，光场图像往往存在高斯-泊松混合噪声，且会有部分缺失．因此，本文首先对HR图像U (·,·,s ,t)进行预处理，使用中值滤波去除坏点，然后基于BM3D高斯去噪滤波器[36]实现Anscombe方差稳定变换去噪，作为本文的真值u，即(·,·,s, t)．为了提高LAC-LFSRnet对LR图像中不同级别噪声的鲁棒性，本文采用了一种混合训练策略来增强数据集，对(·,·,s ,t)进行直接下采样，得到(·,·,s, t)，将(·,·,s, t)和原始的LR图像V (·,·,s, t)共用作为LACLFSRnet网络的输入y(0)．也就是说，位于角度的真值对应着两组输入，构成两个训练数据对

本实验使用10组光场图像Un(x, y ,s ,t )(n =1, 2,…, 10), N = 415, M =13，每组具有169个角度分布，因此训练对的总数 Ntrain为3380．超分辨率的倍数设置为5．进入网络之前对训练数据进行归一化处理.

3.2 网络训练细节

本文使用GPU加速的Pytorch框架训练LACLFSRnet. LAC-LFSRnet的总层数L设置为20．损失函数定义为

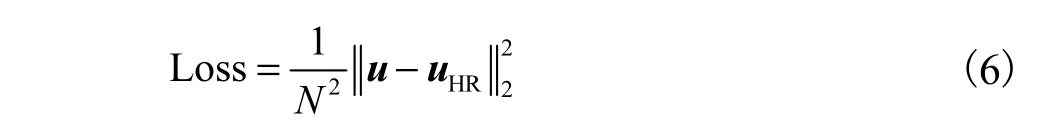
式中：uHR是整个LAC-LFSRnet的输出；N表示uHR的尺寸．实验设置总训练轮数(epoch)为40．训练过程的梯度更新算法为：前20个epoch选择Adam，后20个epoch选择随机梯度下降(stochastic gradient descent，SGD) ．学习率设置为 0.0001(epoch/30)．本实验没有使用特殊的权重初始化方法或其他训练技巧．

3.3 实验结果对比

本文将LAC-LFSRnet的结果与当前主流的超分辨率方法进行对比，包括BM3D＋Bicubic、SRCNN[37]、FSRCNN[38]、RED30[39]、MSRN[40]和EDSR[41]．根据上文的实验设置，所有模型进行重新训练．在测试阶段，将原始LR即不同角度的V (·,·,s, t )输入网络，使用峰值信噪比PSNR衡量超分辨率的效果．在光场图像中，位于边缘角度的图像可能在后续重建等处理中被忽略，最重要的是处于中间位置的图像．由于斑马鱼光场数据集的角度为13，因此本文选择处于整个光场最中心位置(x ,y) =(7,7)的单张图像作为测试图像．

表1展示了本文的模型与其他现有模型在斑马鱼光场数据集中间位置图像上的超分辨率结果．图2给出相应的视觉效果．以上结果表明，在给定实验条件下，LAC-LFSRnet模型表现良好，PSNR远高于其他方法．这可以归因于LAC-LFSRnet比其他网络拥有更多的层数和更深的网络，从而提高了恢复真值细节的能力．图2结果表明LAC-LFSRnet在处理带有轻微噪声的图像时可以更好地恢复纹理细节．

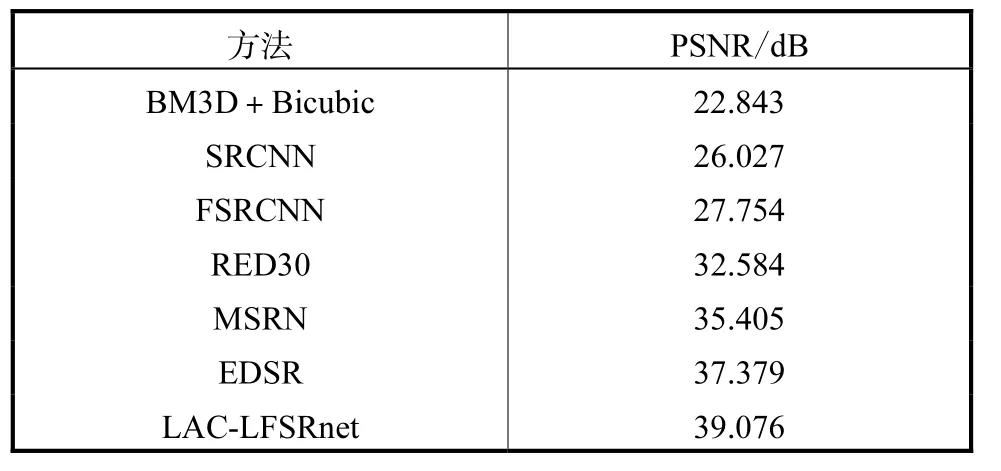
表1 不同方法在斑马鱼数据集上的定量比较结果Tab.1 Quantitative comparisons of different methods on the zebrafish dataset

图2 不同方法在斑马鱼数据集上的视觉效果比较 Fig.2 Comparison of visual effects of different methodson the zebrafish dataset

由于斑马鱼数据集本身存在一定噪声，本文使用无明显噪声的果蝇光场数据集进一步探究LACLFSRnet和LADMM传统优化方法在处理图像超分辨率问题上的表现．除了训练数据对变为{V (·,·,s, t )、U (·,·,s, t )}外，此处和斑马鱼光场数据集实验具有相同的训练策略及参数设置．表2列出基于L2平方范数正则化的LADMM方法、基于频域快速解法的LADMM＋FFT算法的运行时间、收敛所需迭代次数和峰值信噪比PSNR，以及LAC-LFSRnet(20层＋有后处理部分)的测试所需平均时间和PSNR．其中，迭代次数最大设置为100．图3展示了LADMM方法和LAC-LFSRnet模型对果蝇数据集超分辨率的结果，并对细节部分进行放大处理．表2和图3的结果表明，基于神经网络的LAC-LFSRnet相比传统的LADMM迭代优化方法具有更快的运行速度和更好的恢复效果．

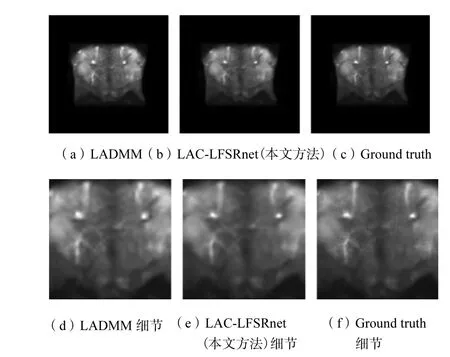
图3 不同方法在果蝇数据集上的视觉效果及细节比较Fig.3 Comparison of visual effects and details of different methods on the drosophila dataset

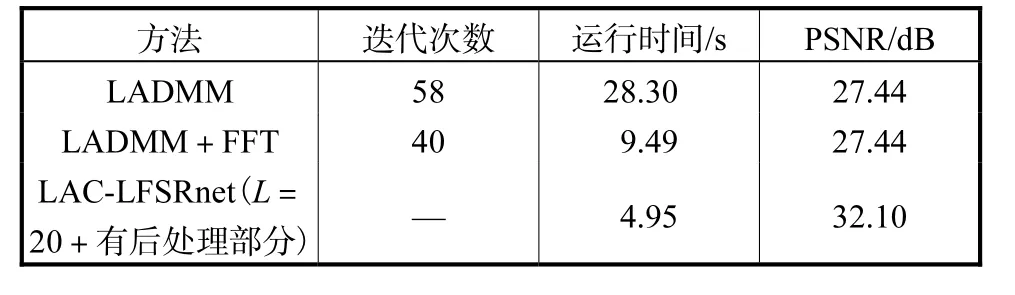
表2 不同方法在果蝇数据集上的定量比较结果Tab.2 Quantitative comparisons of different methods on the drosophila dataset

3.4 消融实验

3.4.1 后处理部分

本文提出LAC-LFSRnet由主体部分和后处理部分组成．后处理部分融合不同层的输出，实现自适应地从主体部分的不同层输出中提取有用的信息．图4表明当主体部分的层数固定时(16、20、22)，有后处 理部分的表现均好于没有后处理部分的表现．

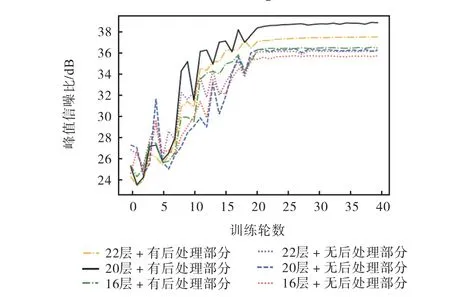
图4 不同网络层数和是否有后处理部分的对比Fig.4 Comparisons of different layers L of the main part as well as with/without postprocessing part

3.4.2 主体部分的层数

本文介绍了LAC-LFSRnet的主体部分是由多层级联组成的．考虑到增加网络深度可能会影响网络性能，本文探索了主体部分的层数L和结果性能的关系．图4表明在有后处理部分的情况下，L＝20时的PSNR比L＝16要高出约2.0 dB，而L＝22时的PSNR比L＝20低1.5 dB．结果表明，主体部分层数从16增加到20会提高结果性能，但网络深度的进一步增加，性能反而会下降．由于L＝20时模型的结果要显著优于其他两种情况．因此本文选择主体部分的层数为20．

3.4.3 主体部分每层后面的细化模块

在本文LAC-LFSRnet中，主体部分的每一层都由LADMM模块和细化模块组成．本文探索了使用细化模块和不使用细化模块的结果差异．如图5所示，经过细化模块的方案比没有细化模块的方案有更好的性能(约0.5 dB)．所以在复杂度允许的条件下可以考虑添加细化模块．

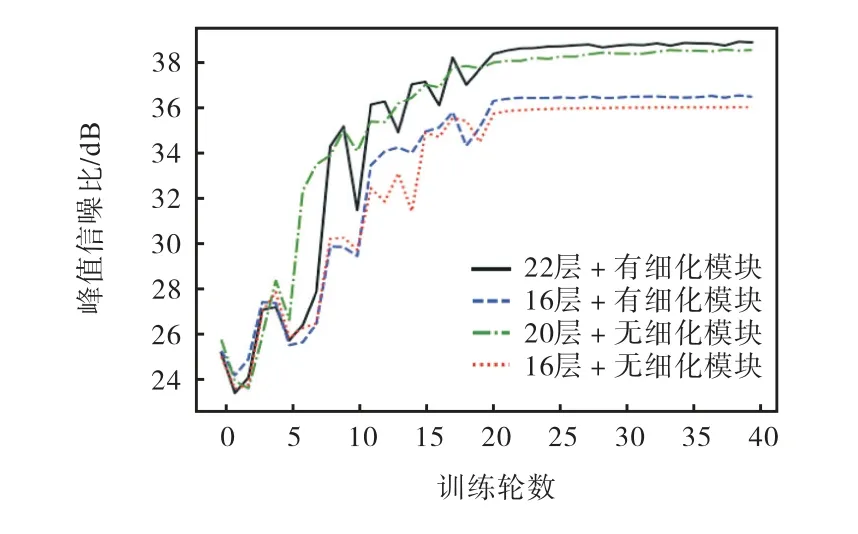
图5 不同网络层数和是否有细化模块对比Fig.5 Comparisons of different layers L of the main part as well as with/without the refinement module

4 结 语

本文提出了一种基于模型方法和基于学习方法相结合的光场超分辨率网络．首先介绍了光场超分辨率模型和传统的LADMM算法．受LADMM算法和卷积神经网络的启发，本文提出了LAC-LFSRnet的网络，详细介绍LAC-LFSRnet模型的具体结构．斑马鱼光场数据集的实验结果表明，LAC-LFSRnet模型同当前主流的图像超分辨率方法相比，具有较好的图像超分辨率处理能力，并且有一定的去噪功能．果蝇光场数据集的实验结果表明，LAC-LFSRnet模型同传统LADMM算法相比，在性能和效率上更具优势．最后，本文还进行了消融实验分析，验证了LACLFSRnet内部结构(后处理部分、细化模块)的有效性.