标准型和改进型DH建模的对比研究与仿真

郭 萍

（武汉交通职业学院智能制造学院，湖北 武汉 430065）

在中国制造2025 的背景下，工业机器人技术进一步发展。机器人运动学建模仿真技术可以动态描述机器人关节的运动特性，直观地显示机器人的运动情况，对机器人的轨迹规划和运动控制研究有重大意义。

1 DH 建模意义

工业机器人的运动学描述就是如何在机器人运动的情况下确定末端执行器的位姿。机械臂是由一系列关节和连杆组成，关节和连杆之间存在相对运动，末端执行器将随着关节和连杆运动，其位姿描述的是一种动态关系。为清晰地表达这种关系，需要确定关节、各连杆和末端执行器之间的运动关系。

建立坐标系可以方便描述运动关系，以机器人末端执行器尖端一点的运动描述为例，尖端点相对末端的位置与末端执行器的尺寸有关，与连杆无关，如果在机器人末端上面建立一个空间坐标系，那么很容易在该坐标系下描述尖端点的位置。然而，连杆和关节是运动的，尖端点相对于连杆和基座的坐标却是不固定的，因此还需要在连杆上建立坐标系，明确连杆坐标系和末端坐标系之间的转换关系。简单、清晰地描述坐标系间转换关系的关键在于建立坐标系。

机器人关节一般有6 个，连杆也有多个，需要建立多个坐标系。为避免坐标系之间的关系复杂多样，须统一坐标系的规则，并且坐标系的参数要尽可能少，根据该原则，DH参数法是比较合适机器人运动学建模的模型。DH 参数法分标准型和改进型，其模型中的每个连杆坐标系只需要4 个参数，因此被广泛应用于工业机器人建模。

2 标准型DH 建模方法

标准型DH 参数法是目前机器人建模的一般方法，是一种描述连杆坐标系的简单且有效的方法，适用于任何机器人结构。

首先，标准型DH 参数法建模确定各个关节坐标系间的变化关系。其次，将所有坐标间的变化结合起来。最后，推导末端坐标系与基座的关系。如图1 所示是机器人中的2 个相邻连杆，在关节处按照DH 参数法建立坐标系。

图1 标准型DH 模型连杆坐标系描述

根据坐标系建立原则（关节轴+1 轴线方向为Z，关节轴和+1 的公垂线所在直线为X，右手法则确定Y轴）可知，X垂直于关节轴，X也垂直于关节轴，由数学知识可知，关节轴垂直于异面直线X和X所在的平面。如果异面直线X和X的夹角为θ，那么坐标系O绕着Z转动θ后，X与X平行。接着，沿着Z移动距离d，X和X重合。下一步，沿着X移动距离a，不仅X与X重合，坐标系O与O的原点也重合，最后绕着X转动α，Z和Z重合, 坐标系O和O完全重合。用数学语言表达该坐标系地转换过程，如公式（1）所示。

将公式（1）展开得到任意相邻坐标系的变换矩阵，如公式（2）所示。

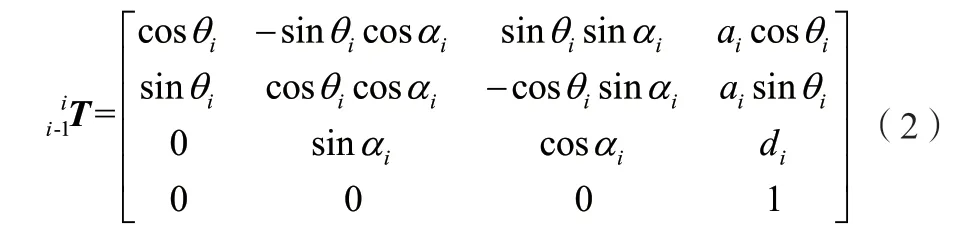
该变换矩阵可以将坐标系O映射到O。在每个连杆上都建立一个坐标系，然后用上述变换关系找到相邻连杆之间的变换关系，就可以描述机器人末端点在基坐标系下的坐标，即DH 参数法仅用、、和这4 个参数就能描述坐标变换。

3 改进型DH 建模方法

与标准型DH 建模法不同，改进型DH 坐标系不是建立在传动轴上的，而是建立在连杆的驱动轴上，即靠近基座一侧的关节轴上。2 种建模法坐标系描述的区别如图2、图3所示。

图2 标准型DH 坐标系

图3 改进型DH 坐标系

改进型DH 建模法的关节、连杆和坐标系按照从基座到末端执行器的方向排列，其顺序为关节1、与关节1 并列的连杆1 坐标系、连杆1 以及关节2，以此类推。

对传统的串联机器人来说，标准型DH 建模方法受到大多数研究者的青睐。但是对非串联结构的机器人来说，标准型DH 建模法并不适用。例如1 个连杆同时存在2 个传动轴，分别连接2 个连杆，如图4 所示。设关节1 和基座之间的连杆编号为0，参考坐标系编号为0。按照标准型DH 建模法，连杆的坐标系在传动轴上面，那么连杆坐标系3 将与参考坐标系0 重合，即在关节1 处将同时建立2 个坐标系，会引起歧义。而采用改进型DH 建模方法，连杆的坐标系在驱动轴上面，各个连杆坐标不会出现重合的问题，如图5 所示。

图4 非串联结构机器人的标准型DH 建模坐标描述

图5 非串联结构机器人的改进型DH 建模坐标描述

不管机器人结构多复杂，每个连杆只有1 个驱动轴，改进型DH 参数法都可以准确的建立坐标系，可解决多个传动轴坐标系无法准确建立的问题。与标准型DH 建模法相比，改进型DH 建立坐标系的位置发生了变化，连杆之间的变换关系自然也有相应的变化，由数学坐标变换知识可得，改进型DH 坐标系相邻连杆之间的变换关系如公式（3）所示。

将公式（3）展开得任意相邻坐标系的变换矩阵，如公式（4）所示。

4 DH 建模的分析与验证

SCARA 是关节型机器人，其具有作业速度快、效率高的特点，被广泛应用于生产和生活中。SCARA 采用1 个移动关节和3 个旋转关节，3 个关节旋转则控制末端执行器前后、左右运动，平面上具有很好的灵活性。为准确地描述标准型DH 建模法和改进型DH 建模法的差异，该文针对SCARA 机器人进行运动学建模并对比仿真。SCARA 各个连杆上的坐标系描述如图6、图7 所示。

图6 标准型DH 模型连杆坐标描述

图7 改进型DH 模型连杆坐标描述

由坐标系间的关系可推出DH 参数表，分别见表1、表2。其中，、、和为变量，其余参数均为固定值。

表1 标准型DH 参数

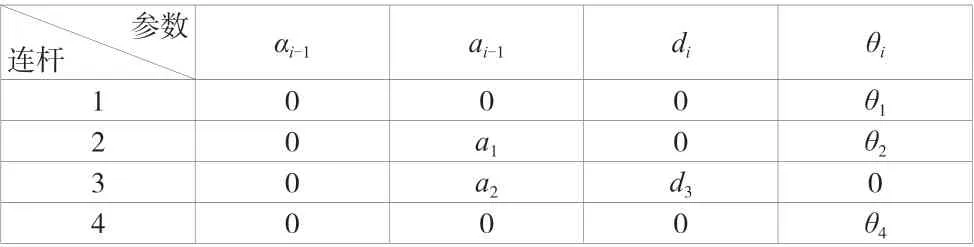
表2 改进型DH 参数

根据DH 建模法，SCARA 机器人末端执行器相对基座的坐标如公式（5）所示。

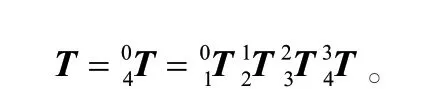
分别将标准型和改进型DH 参数带入公式（2）和公式（4）并进一步求得总变换矩阵，经推算，标准型DH 建模法和改进型DH 建模法得到的总变换矩阵一致，如公式（6）所示。

理论上，通过总变换矩阵可推算出末端执行器的坐标，便可进一步描述末端执行器相对于参考坐标系的运动。总变换矩阵一致说明标准型和改进型DH 建模在描述末端执行器模型，如图8 所示，通过对比再次证明2 种DH 参数仿真模型的一致性。根据所建立模型，采用多项式进行轨迹规划并进行运动仿真，结果表明2 种模型所得到的末端执行器的运动轨迹是一样的，如图9 所示。因此，不论是标准型DH 建模还是改进型DH 建模，尽管连杆的坐标系描述不一样，但是最终的运动学描述效果是一样的。

图8 SCARA 机器人的SDH 和MDH 运动学模型

图9 SCARA 末端执行器的运动轨迹

5 结语

该文通过研究标准型和改进型DH 参数建模法，以SCARA 机器人运动学建模与仿真为例，得出2 种参数建模法在理论和仿真效果上具有一致性的结论，因此，对一般的串联机器人来说，标准型DH 和改进型DH 模型没有优劣之分。然而随着机器人技术的发展，机器人的结构越来越复杂，对的运动方面的效果是一样的。

为进一步验证效果的一致性，采用MATLAB 分别搭建基于标准型DH 参数（SDH）和改进型DH 参数（MDH）的树结构、闭环结构这种非串联型机器人来说，改进型DH 模型可以避免坐标系歧义问题，更准确地描述机器人的运动，更适合在运动学建模中应用。