抗蛇行减振器节点刚度对列车转向架横向振动特性的影响研究

陈国泰，卢 婧，程 刚

(1.中国铁路西安局集团有限公司 西安客车车辆段，陕西 西安 710024；2.中国石油天然气股份有限公司 长庆油田分公司，陕西 西安 710000)

采用抗蛇行减振器是抑制转向架蛇行失稳的重要手段，抗蛇行减振器纵向安装于车体与转向架之间，通过提供二系回转力矩来提高铁道客车系统的稳定性，因此成为铁道客车重要的悬挂元件[1-2]。过去对于车辆系统的建模，较少考虑减振器两端橡胶节点的弹性，在模型中多作为刚性来处理。但在实际的车辆系统中减振器两端都加有橡胶弹性节点，其目的是一方面提高系统的隔振和降噪能力；另一方面是避免减振器两端相连部件如轮对、转向架和车体其他方向的振动影响减振器正常工作，从而延长减振器的使用寿命[3-6]。抗蛇行减振器两端与转向架、车体的连接接头有5种，分别为橡胶垫式、球形桥式、球形销式、无外套桥式和无外套销式，具体用哪种形式需要根据其安装位置和与之连接体的结构决定。减振器节点刚度在连接体的x、y和z方向上均有分布，通常对其进行简化，只考虑其安装方向的安装刚度，忽略其他方向的刚度。

抗蛇行减振器是车辆悬挂系统中非常重要的悬挂元件，建立合理的模型并与车辆模型结合起来研究转向架横向振动特性是非常有必要的。本文将建立17自由度列车横向振动系统模型，并且将抗蛇行减振器Maxwell模型引入其中，得到改进后的列车横向振动系统模型，应用随机振动理论来分析研究抗蛇行减振器节点刚度随着频率的变化对列车转向架横向振动特性的影响，以期为抗蛇行减振器节点的结构设计和相关振动参数的优化提供参考和依据。

1 抗蛇行减振器橡胶节点弹性悬挂的数学模型

考虑车体和转向架的结构，用数学模型展示减振器两端橡胶节点弹性悬挂。图1为质量-弹簧-阻尼系统，其中k和k0为悬挂系统弹簧刚度，c和kr分别为减振器阻尼和橡胶节点刚度，m1为车体，m2为构架，z1和z2分别为m1和m2的位移，z3和z4是抗蛇行减振器2个橡胶节点连接处的位移，u为外界输入不平顺激励。

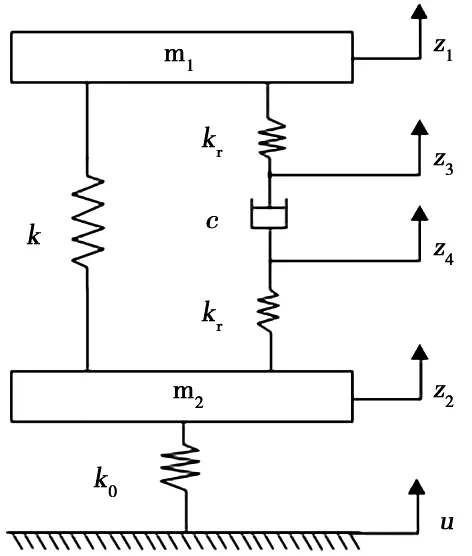
图1 质量-弹簧-阻尼系统

由动力学定律，可得出图1所示系统的运动微分方程组：

(1)

令Δz=z3-z4，变换关系为：

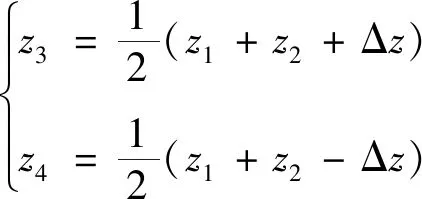
(2)

代入式(1)后，得：

对于列车横向振动系统，一系和二系悬挂均安装有减振器，可运用该数学模型的方法进行分析。

2 列车横向振动系统的模型建立

基于对力学模型简化的基本原则，简化后的列车横向振动系统计算分析简图如图2所示。仿真条件假设车体与转向架当作刚体，轮轨为刚性接触，忽略零部件的柔性属性；车辆行驶过程中轮轨一直是相接触的；抗蛇行减振器视为非线性元件，其他悬挂元件是线性的；车体与转向架的位置在笛卡尔坐标系中纵向和垂直平面内与其质心对称；仿真过程中车辆是匀速直线行驶的，主要考虑车辆各部分在横向平面中的振动，忽略垂向的弱耦合作用。

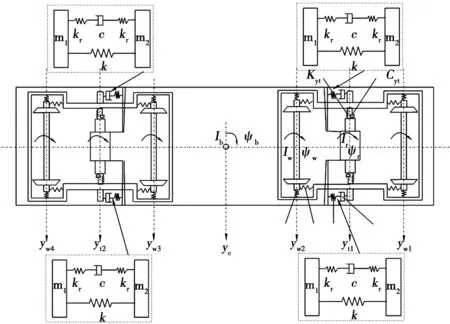
Kyt.二系悬挂横向刚度；Cyt.二系悬挂横向阻尼；yw1、yw2.、yw3、yw4.1位、2位、3位、4位轮对横向运动位移；yt1、yt2.1位、2位构架横向运动位移；yc.车体横向运动位移；Ib、Iw、Ir.车体、轮对、构架的侧滚角位移；Ψb、Ψw、Ψr.车体摇头角位移。

整车总共17个自由度，转向架二系悬挂2个抗蛇行减振器，计算转向架摇头作用力时，其等同于1个抗蛇行减振器作用力的2倍，在推导方程时只需增加1个抗蛇行减振器的相对位移量。横向减振器做同样处理，横向振动中考虑4个相对位移量，这样即可得到向量形式的微分方程组：

(4)

式中：y——系统的自由度向量；

y1——减振器相对位移向量；

Fc，Fg,f(t)——整车门自由度向量矩阵；

M，C，K——分别为质量矩阵、阻尼矩阵、刚度矩阵。

3 多点完全相干平稳激励的虚拟激励法

与传统的车辆随机振动随机响应的分析方法相比较，虚拟激励法具有计算简单、计算量小的特点。而虚拟激励法同样在轨道车辆振动中也得到了相关应用，车辆运行中轮对接触钢轨产生的作用力被认为只是时间前后的差异，轮对所受力的大小方向是相同的，这样可以高效准确地解决车辆横向振动问题。

针对多轮对轨道车辆，应用多点完全相干平稳激励的虚拟激励法。设4条轮对异相位平稳随机激励为f(t)，得到：

(5)

式中：ai——轮轨接触点处激励强弱的系数，且4条轮对受到的激励强度相同，令ai=1；

F(t)——时间历程函数；

ti——系统受力前后时间差常数，i=1，2，3，4。

(6)

式中：i——1～4位轮对；

ω——圆频率；

SFF(ω)——自功率谱密度函数。

轨道车辆的动力学方程具有的一般形式：

(7)

将式(6)代入式(7)可得：

(8)

得到响应的功率谱Syy为：

(9)

通过ω和f的转化可得到加速度功率谱密度响应，以矩阵形式表示为：

(10)

系统振动位移的功率谱密度矩阵可表示为：

(11)

式中：*——复共轭，取ω=2πf。

通过转化得到系统加速度功率谱密度矩阵：

(12)

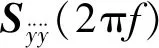
4 数值分析

4.1 车辆与轨道条件

以某型轨道客车为例，其横向模型主要参数见表1，以美国Ⅵ级轨道方向不平顺作为横向振动模型频域研究的仿真激励，其功率谱密度曲线如图3所示。

表1 某型轨道车辆横向模型主要参数

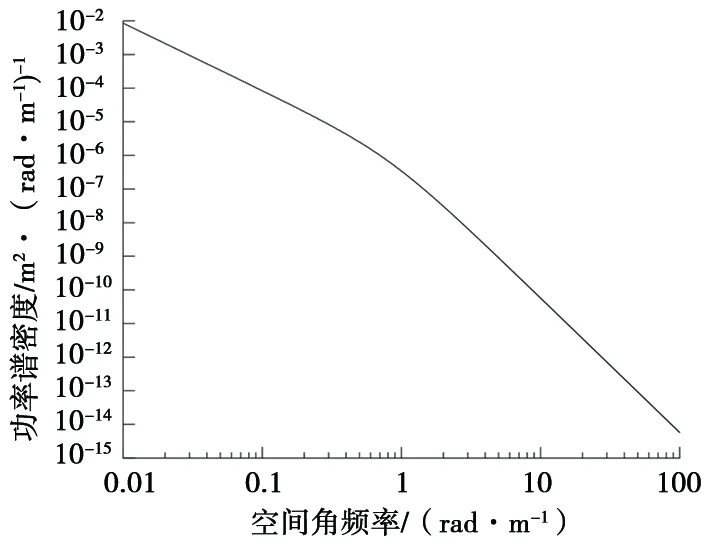
图3 美国Ⅵ级轨道方向不平顺的功率谱密度曲线

4.2 仿真计算与结果分析

设定车辆直线行驶速度分别为60 km/h、120km/h、160 km/h，含Maxwell抗蛇行减振器模型的17自由度横向振动系统改进模型的参数值保持不变，对其转向架在频域内的振动特性进行仿真研究。

图4为客车以不同速度运行时，前后转向架的横移、侧滚、摇头位移功率谱密度曲线。从图4中可以看出，在不同运行速度下，前后转向架横移、侧滚、摇头位移功率谱密度随速度的变化趋势大致相似，但其对应的功率谱密度有所不同。随着客车运行速度的变化，车速与前后转向架的位移功率谱密度呈正相关。由此可见：客车运行速度是影响转向架横向振动的一个重要因素。从图4中还可以看出，前后转向架位移功率谱密度峰值均在2～10 Hz内出现，因此影响前后转向架横移、侧滚、摇头振动的频率范围较低。

图4 不同车速下前后转向架位移功率谱密度曲线

保持车辆振动系统模型不变，车辆运行速度为120 km/h时，抗蛇行减振器节点刚度原参数为35 MN/m，其他参数均为固定值，分别取原值附近2个刚度值17.5 MN/m、70 MN/m，通过对抗蛇行减振器节点刚度值下的车辆振动系统进行仿真，得到前后转向架横向振动的频域响应。

图5为车辆在不同抗蛇行减振器节点刚度下的前后转向架横移、侧滚、摇头加速度功率谱密度曲线。由图5可以看出，在不同抗蛇行减振器节点刚度下，前后转向架横移、侧滚加速度功率谱密度随节点刚度的变化差异较大，其对应的功率谱也有所不同。在0～40 Hz内，抗蛇行减振器节点刚度值越大，前后转向架横移和侧滚加速度功率谱密度越小，与节点刚度呈负相关。前后转向架摇头加速度功率谱密度在0～5.5 Hz内随着抗蛇行减振器节点刚度增大而增大。由此可见，在不同频率范围内，抗蛇行减振器节点刚度的取值对转向架横移、侧滚、摇头加速度功率谱密度影响显著。

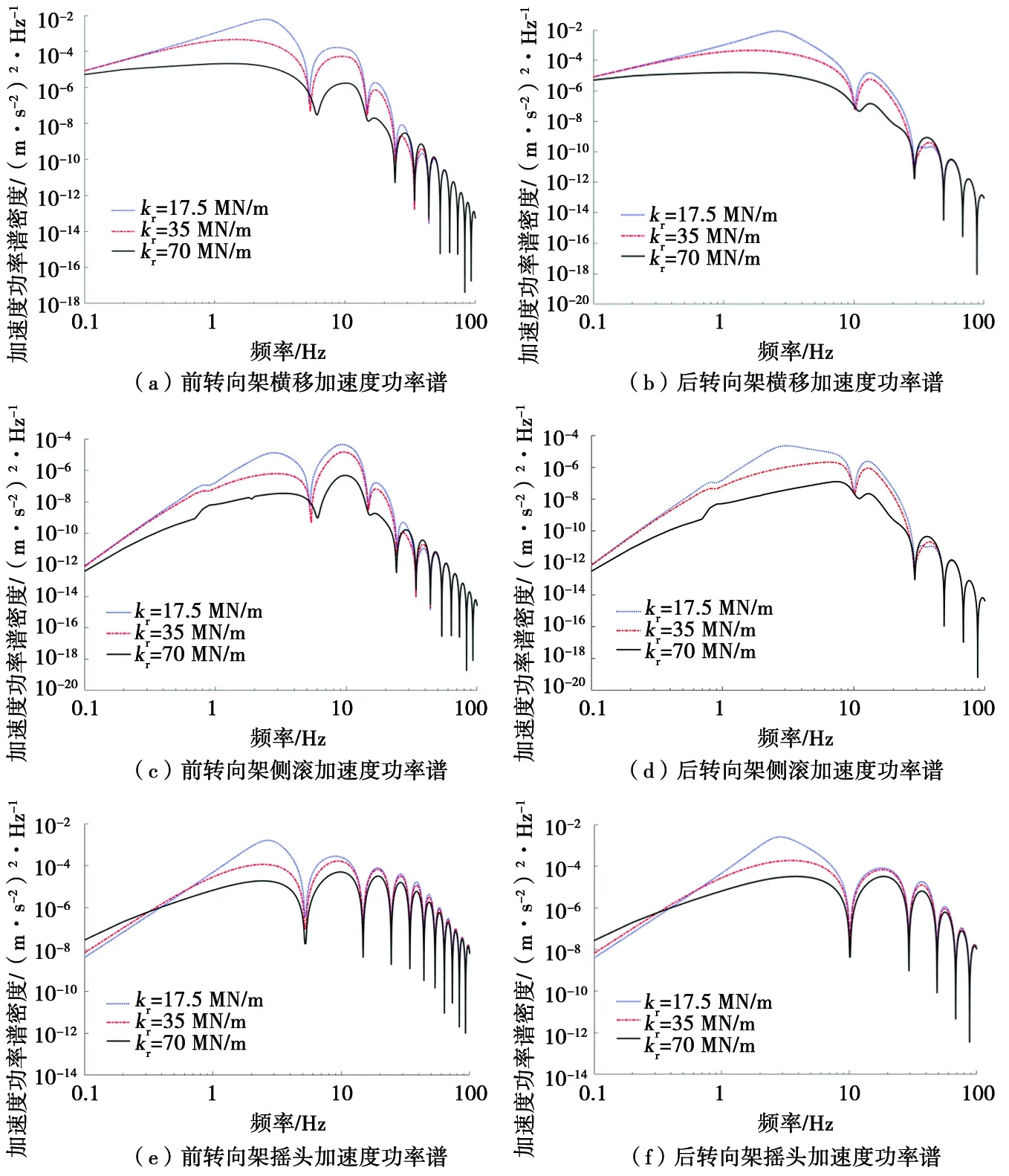
图5 不同节点刚度下前后转向架加速度功率谱密度曲线

5 结论

列车运行速度是影响轨道车辆横向振动系统转向架横向加速度功率谱的一个重要因素。随着运行速度的提高，前后转向架横移、侧滚、摇头位移功率谱密度和振动主频均增大，而且影响前后转向架横移、侧滚、摇头振动的频率范围较低。当选取不同抗蛇行减振器节点刚度时，前后转向架横移、侧滚、摇头加速度功率谱密度变化相对于节点刚度取值非常敏感。因此，在不同频率范围内，合理选择抗蛇行减振器橡胶节点刚度有利于减小转向架功率谱密度，能够有效提高转向架横向运动的平稳性。