盾构法重叠隧道施工过程中施工顺序及施工间隔对土体变形的影响研究

范 奇，张天奇

盾构法重叠隧道施工过程中施工顺序及施工间隔对土体变形的影响研究

范 奇，张天奇

(天津大学建筑工程学院，天津 300350)

随着我国地下工程的持续开发建设，城市地下空间变得愈发拥挤．城市地铁上下行双线隧道在面对狭窄的地下空间环境限制时，有时需要采取重叠隧道的形式进行施工．由于双线隧道重叠布置，施工引发的土体变形产生叠加效应，因此重叠隧道施工引发的地表沉降更难控制和预测．同时，由于双线隧道重叠一般是为了应对狭窄的空间，因此重叠隧道通常会临近其他结构物施工，如建筑基础、管线和其他隧道．本文以天津地铁5号线程津段重叠隧道工程为背景，建立了精细化模拟的有限元数值模型，考虑了盾构掘进过程中掌子面支撑、盾构摩擦、盾构推力、盾尾注浆和台车重量等施工因素．计算结果与实测数据行了对比验证，证明了数值模型的可靠性．借助该数值模型对重叠隧道施工顺序与盾构施工参数的关系展开研究，优化了已有研究得出的简单定性结论．对重叠隧道双线隧道同步施工时不同施工间隔进行评估，从地表沉降、沉降发展速率、隧道位移和收敛等方面进行了分析，结合统计学方法和施工实际情况给出了推荐的重叠隧道施工间隔方案，应用该结论可以帮助重叠隧道施工节省近一半工期成本．

重叠隧道；施工顺序；施工间隔；现场实测

随着现代城市地下空间的不断开发，城市地下空间正在变得越发拥挤．当地铁线路穿越拥挤地段时，上下行的双线地铁隧道有时不得不采取双线重叠的形式进行施工．目前国内已有多个盾构重叠隧道设计与施工的先例，如表1所示．

表1 重叠隧道施工案例

Tab.1 Cases of overlapping tunnel constructions

重叠隧道施工研究中，一个讨论较为广泛的问题就是重叠隧道施工顺序问题，然而已有重叠隧道施工顺序研究中，得到的结论并不一致．

国外学者Addenbrooke等[1]、Chehade等[2]建立了重叠隧道二维数值模型，研究了不同隧道间距条件下的地表沉降及隧道自身的变形．计算结果认为重叠隧道“先上后下”比“先下后上”施工引起的地表沉降要大．

Do等[3]使用三维数值模拟方法研究了软土中重叠隧道施工对先建隧道和周围土体的影响，计算结果发现上线隧道先施工会比下线隧道先施工产生更大的地表沉降．马少坤等[4-5]结合数值模拟方法与离心机模型试验，得到了与Do等[3]一致的结论，重叠隧道“先上后下”施工比“先下后上”施工地表最大沉降值大约18%．郭晨[6]、金乃麒等[7]国内学者通过三维数值模拟方法得到了相似的结论，即“先上后下”施工地表沉降较大．

陈平[8]、范晓真等[9]计算重叠隧道两种不同施工顺序，认为沉降值基本相近．

江宇等[10]结合深圳地铁3号线工程，利用数值模拟方法对比了“先下洞，后上洞”和“先上洞，后下洞”两种施工顺序，通过计算结果得知，“先上后下”地表横向沉降量比“先下后上”小．随着计算隧道掘进距离的变化，该差值比例也在变化(27%～50%)．

以上研究的具体方法与关键结论如表2所示．通过分析和比较，本文更倾向于三维模型的计算结论，因为它考虑了隧道掘进方向的力学行为，同时也考虑了隧道结构的纵向刚度的影响．但已有三维数值模拟研究仍对重叠隧道施工顺序问题有不同结论，然而不同研究中的模拟方法区别较大，因此仍需进一步对该问题展开研究．

表2 重叠隧道施工顺序研究结论

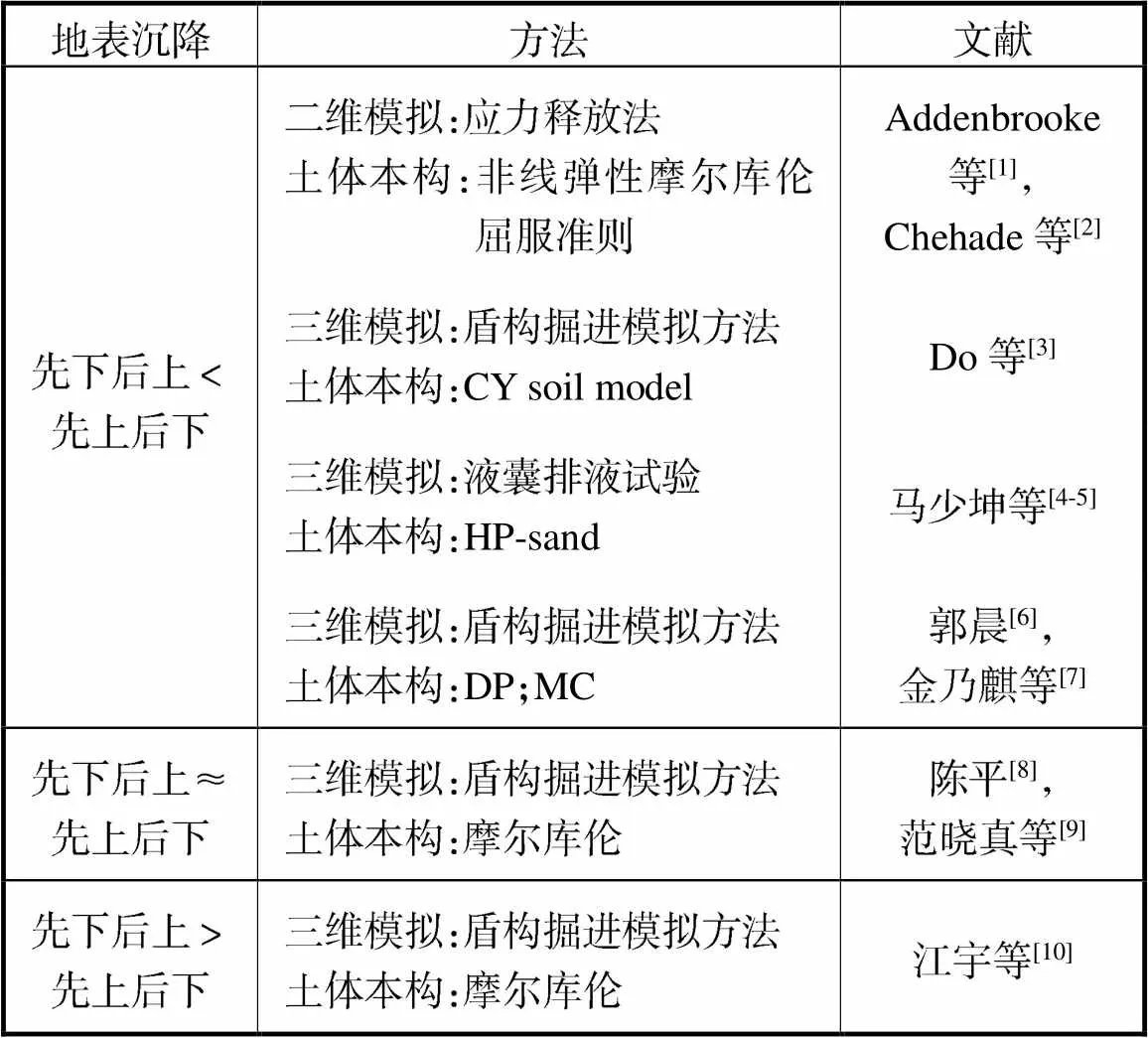
Tab.2 Research conclusions on the construction sequence of overlapping tunnels

针对已有研究结论对重叠隧道不同施工顺序引发的地表沉降大小关系存在的分歧，本文以天津5号线程津段重叠隧道工程为背景，建立了精细化模拟的有限元数值模型．对重叠隧道施工顺序对地表沉降影响问题展开研究，重点分析了盾构施工参数与隧道属性对于该结论的影响．

实际工程中该重叠隧道工程采用先下线后上线的施工顺序，自下线隧道盾构机始发至上线隧道贯通完成，工期总耗时1年8个月零5天．目前盾构双线平行隧道已有并行施工先例及相关研究[11]，但由于缺乏重叠隧道同步掘进的理论研究和工程经验，程津段采用较为保守的施工方案，先建隧道贯通后再进行后建隧道的施工．因此尽管单线隧道掘进完成仅需7个月，但重叠双线隧道施工完成却需要近2年．因此本文借助数值模型，对重叠隧道上下线隧道同步施工时不同施工间隔影响展开，分析了不同施工方案土体变形及隧道变形，结合相对差距和方法对不同施工间距方案进行综合评价并给出推荐的施工间隔方案．

1 工程概况

天津地铁5号程林路站到津塘路站区间重叠双线隧道全长1348m．由于隧道线路紧邻东风立交桥和周围建筑，地铁上下行双线隧道按照竖向重叠的方式进行设计和施工．参考以往的类似重叠工程经验与相关研究，采用了先下线后上线的施工顺序，上线隧道在下线隧道施工完成后开始掘进．本工程使用了两台长度为8.7m、直径为6.4m的土压平衡盾构机．隧道由预制混凝土管片拼装，单环管片1.2m长，内径和外径分别为5.5m和6.2m．

本文选择了一块空旷场地(greenfield)作为研究场地，如图1所示．场地布置地表沉降测点，地表沉降监测共布置4个监测面，监测面与隧道线路垂直．

表3给出了该场地横向截面的土层分层情况及参数，数据由岩土钻孔勘探得到．土层1为人工填土，土层2、3、5、7为粉质黏土，其他土层为砂质粉土．场地的地下水为静水力梯度，地下水水位线位于地表以下1m以内．土体主要分为8个土层，最上层为1.6m厚的人工填土，下方土层以黏土与粉土为主．下线隧道和上线隧道的轴线深度分别为26.1m和13.4m，两条隧道掘进主要穿过粉土层．

盾构机穿越研究场地时施工参数如表4所示，为区间施工参数的平均值．

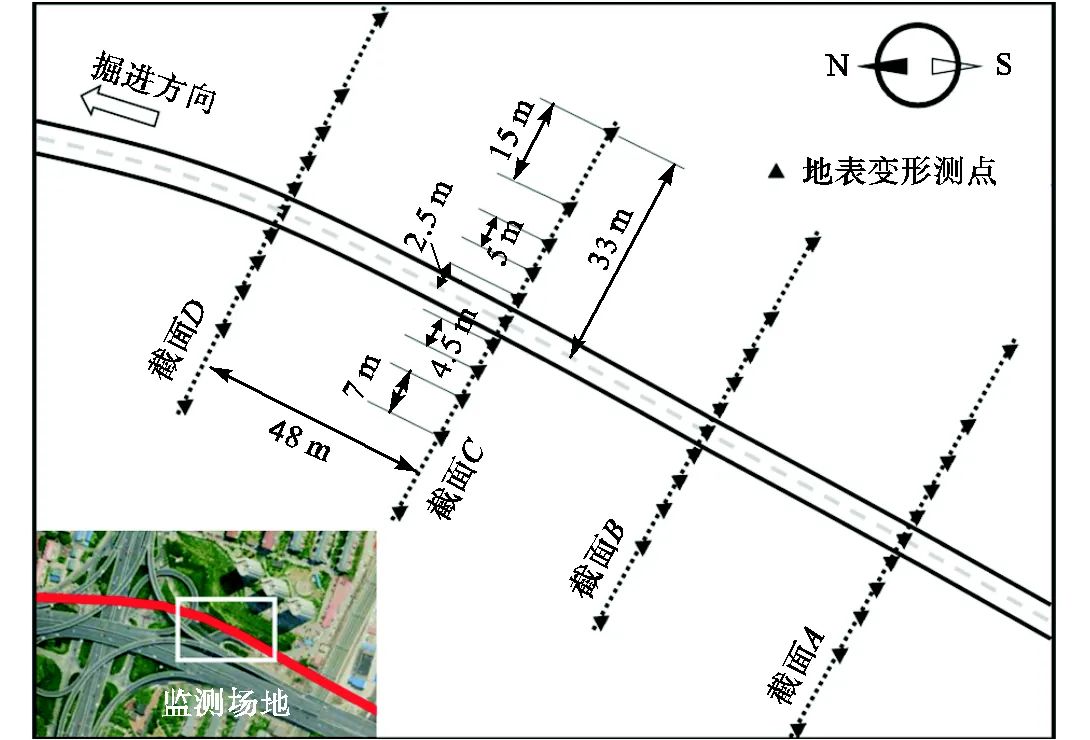
图1 研究场地与监测点布置

表3 土层参数

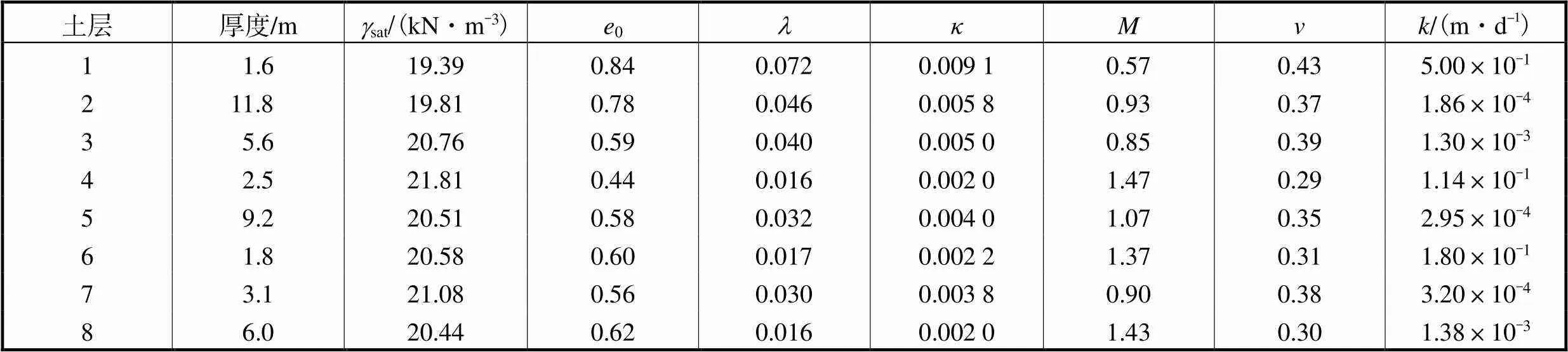
Tab.3 Soil profile

表4 盾构机施工参数

Tab.4 Shield construction parameters

2 数值模型

2.1 模型网格及边界条件

本节的数值分析使用商业数值软件ABAQUS进行水土耦合的有限元分析计算．ABAQUS提供了方便的二次开发程序接口，可以定义新的材料属性．图2给出了用于模拟重叠双线隧道施工三维有限元模型的网格及尺寸．模型包括79180个八节点六面体实体单元(C3D8P)，用于模拟土体和注浆体；6848个四节点四边形壳单元(S4)，用于模拟管片和盾构机.模型土体长为120m(100环)，宽为86.4m(13.5，为盾构机直径)，高为64m(10)．该尺寸取值参考Franzius等[12]对模型尺寸及边界影响的分析，可以满足隧道开挖模拟对模型尺寸的要求．由于该场地及隧道以隧道纵轴面对称，所以模型建为半模型．模型底面采用纵向位移约束，对称面的边界为对称边界，其余侧边界对法向位移进行约束．参考岩土勘察结果，对水位线高度进行简化，设置在土体表面，孔压固定为0．由于本节工作不考虑土体的长期响应，隧道管片均考虑为不透水边界[13]．

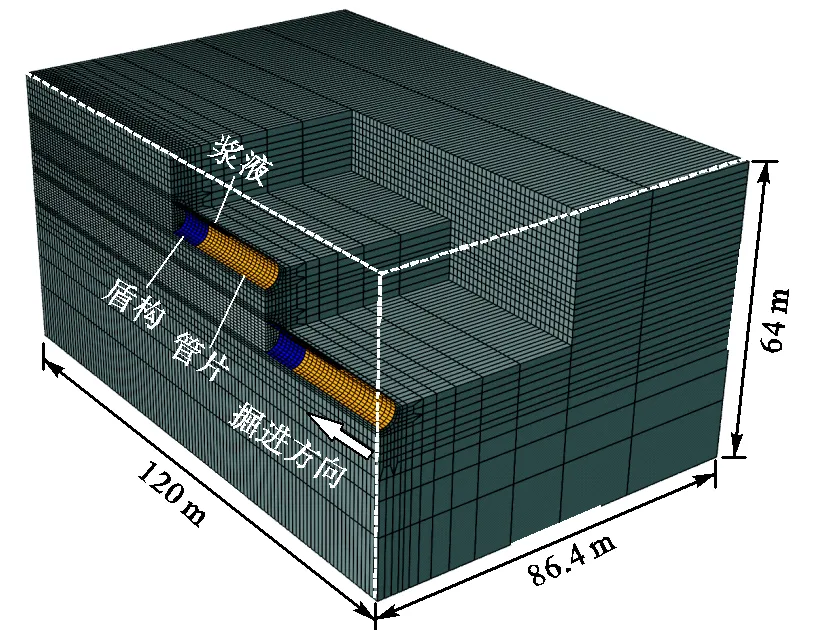
图2 有限元数值模型网格及尺寸

2.2 土体本构

修正剑桥模型是软土模拟中应用较为广泛的本构模型，由于其使用孔隙比描述土体变形，所以更加适用于水土耦合分析．修正剑桥模型也已多次应用在天津软土隧道开挖问题的模拟中[14-15]，有效性和准确性得到了验证．所以本节工作采用修正剑桥模型对土体进行模拟，各土层的修正剑桥参数见表3．其中压缩系数和回弹系数通过压缩回弹试验得到．临界应力比由不排水三轴压缩试验测得．土体考虑为正常固结土，土体水平向压力系数0由杰西公式(Jaky’s equation)计算得到．土体的渗透系数通过定水头渗透试验测得．

2.3 盾构机及管片模拟

本工程使用的土压平衡盾构机长8.7m，重量为4500kN．为了方便盾构机与管片单元共用节点，提高计算效率，将盾构机模型优化为8.4m，等于7个环管片的长度．因此，盾构机单元设置为重度270.6kN/m3、厚度为0.1m的壳单元，弹性模量为21000GPa，忽略盾构机变形．

隧道管片为宽度1.2m、厚度0.35m的C50混凝土预制管片．本节模拟未考虑管片接头及拼装结构，隧道用厚度0.35m的壳单元圆管进行模拟，重度25kN/m3，本构选用正交各向异性模型，特点是在某个横截面内为各项同性而面法线方向为不同性．Lee等[16]使用刚度折减法将拼装管片结构的隧道等效为均质圆管．参考他们的研究工作，取0.75的折减系数用以考虑管片拼装过程时隧道的刚度损失．参考Shiba等[17]的研究，隧道纵向刚度取0.1的折减系数用于考虑拼装结构的纵向刚度折减．纵向刚度n＝0.1con，其他向刚度p＝0.75con，其中混凝土刚度con＝34.5GPa，本文暂不考虑对管片剪切模量的折减，管片泊松比取0.2．

2.4 注浆模拟

盾尾注浆模拟过程主要包括两个重要因素，即注浆压力和浆液硬化过程．注浆体采用时间相关的多孔弹性实体单元进行模拟，注浆压力用盾尾处的孔压边界进行模拟[18-19]．浆液自盾尾注入盾尾间隙后，注浆体的硬化过程用时间相关的弹性模量和渗透系数进行描述．注浆体的刚度可以由下式表达：

()＝(28)E()(1)

式中：(28)为浆液硬化28天后的弹性模量；E()为时间相关的系数，具体数值见文献[20]．

时间相关的渗透系数可以由下式表达：

()＝((0)－(28))e-0.535t＋(28)(2)

式中：(0)为浆液刚经过注浆孔注入时的渗透系数；(28)为浆液硬化28天后的渗透系数．

2.5 隧道开挖模拟步骤

本文中双线隧道开挖均采用step-by-step模拟方法[18]．根据实际施工速度，下线隧道和上线隧道掘进速度分别为0.2天/环和0.15天/环．如图3所示，每一个隧道开挖步过程如下．

(1) 移除新开挖面前的土体单元，同时取消旧开挖面的掌子面支撑力．

(2) 盾构模型前进至新开挖面．对新开挖面施加掌子面压力．掌子面压力竖向梯度为10kPa/m，上线隧道轴心处掌子面压力为122kPa，下线隧道轴心处掌子面压力为254kPa．盾壳与土体间的摩擦力由总推力减去掌子面力计算得到，并作用在盾壳与土体之间的节点上．上线隧道与下线隧道的节点力分别为218kN和272kN．

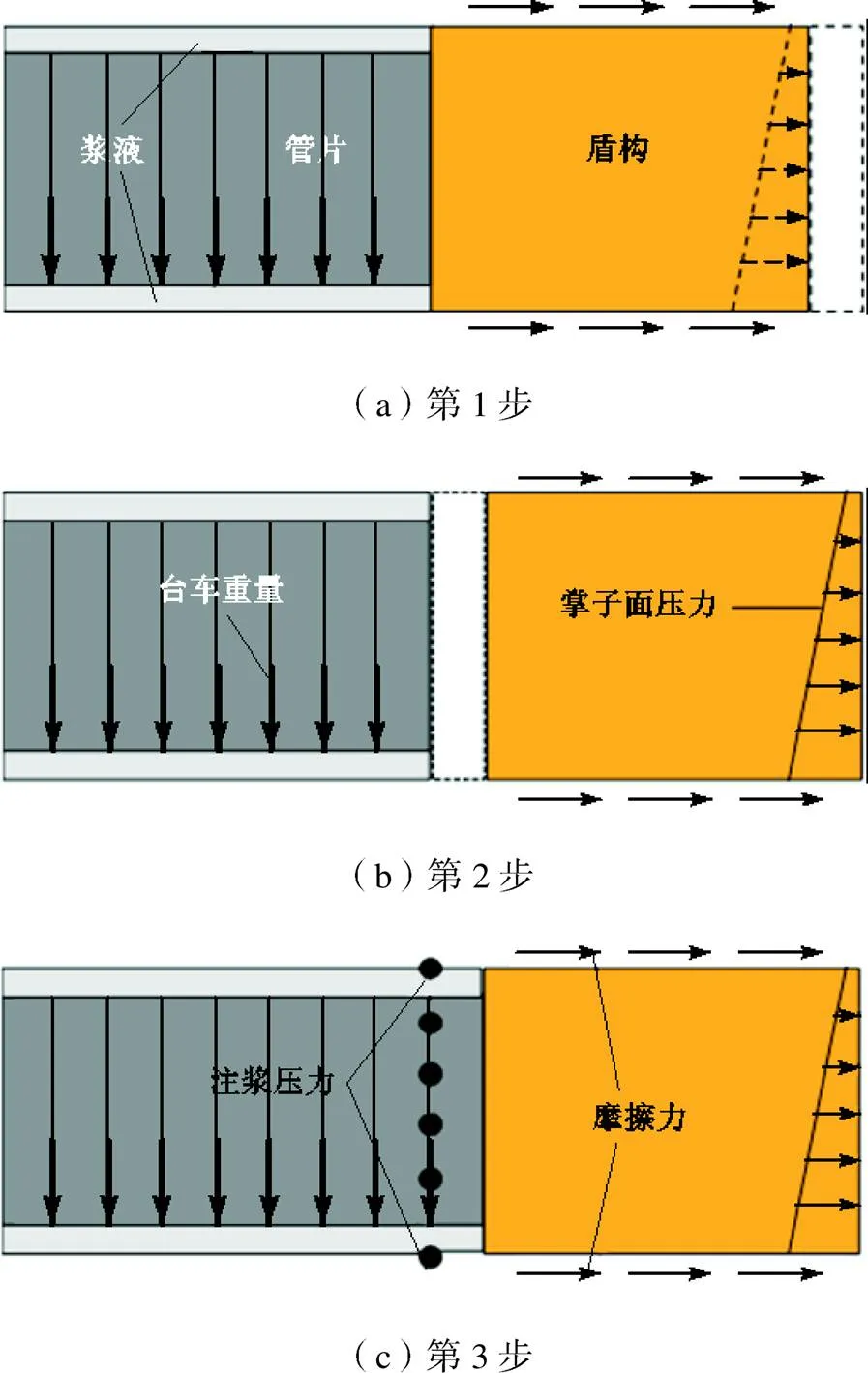
图3 模拟开挖步骤

(3) 盾尾后方生成壳单元管片并同时激活浆液单元．同时，注浆压力作为孔压边界施加在盾构尾部的注浆体单元上．考虑到浆液注入时受到管路等设备的阻力，实际注入土体的压力比设备记录压力小.因此，数值模拟中的注浆压力较施工记录注浆压力进行了80kPa的折减[15]．注浆压力竖向梯度取10kPa/m，上线隧道和下线隧道轴线深度注浆压力分别为183kPa和294kPa．

上述模拟步骤在每一个开挖步进行重复，模拟盾构隧道开挖过程．台车重量3300kN，长度为60m，连接在盾构尾部通过临时轨道运行．台车重量用轨道分布位置的竖向力进行模拟．

3 地表沉降

图4为盾构施工不同阶段监测结果与数值计算结果得到的土体横向沉降槽．图中数值计算为模拟实际工程施工过程的计算结果．图4(a)和(b)分别给出了下线隧道和上线隧道施工引发的净沉降．图中实测数据与计算结果分别为不同颜色的点与线，实测数据为截面～的平均值．数值结果为模型第40环正上方监测截面的土体沉降．可以看出，数值计算结果与实测结果拟合良好．总地来说，相较于下线隧道，上线隧道施工形成的沉降槽更窄更深．值得注意的是，上线隧道盾构到达监测面前，距离隧道中心20m处有轻微隆起．该现象可能是上线隧道相对较大的掌子面压力和浮力作用造成的隧道上浮引起的.

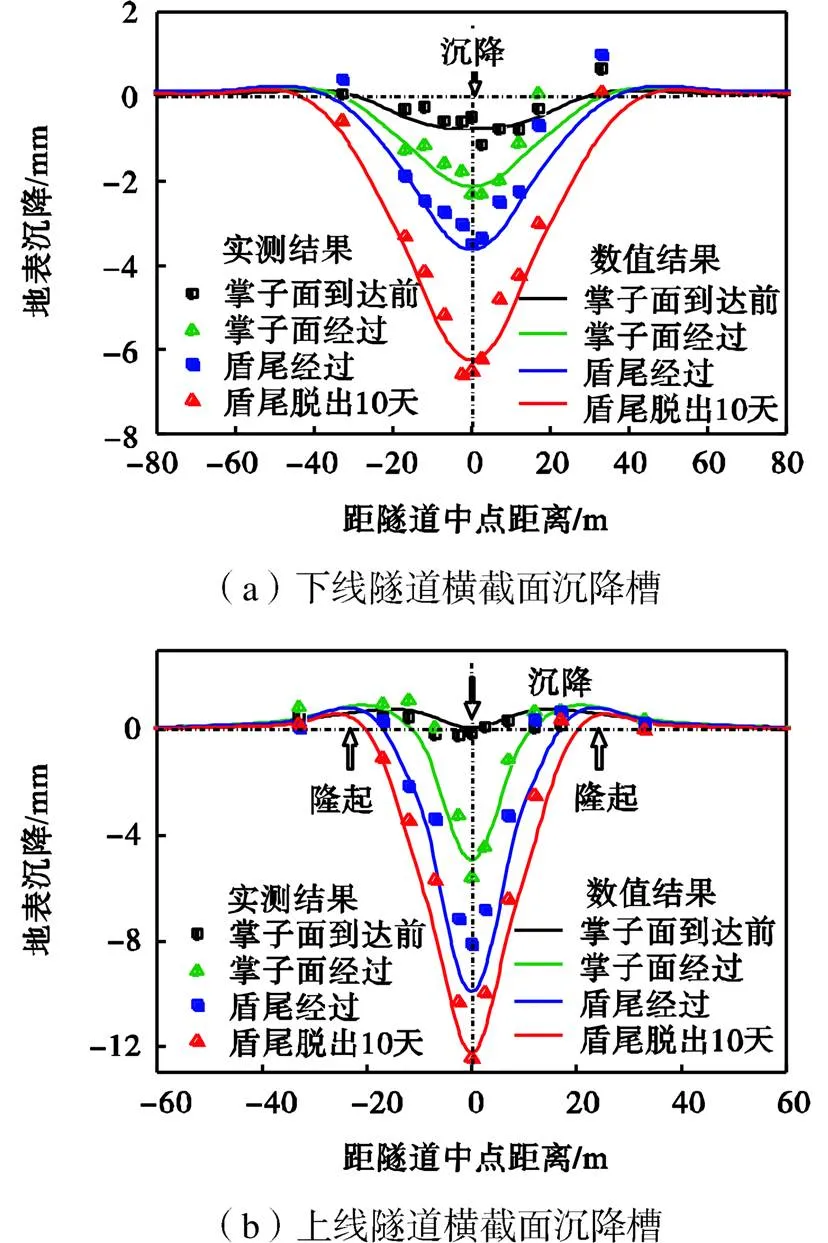
图4 实测与计算地表沉降

由于实际工程施工过程无法重复，因此借助数值模型分析了天津5号线程津段重叠隧道不同施工顺序下土体沉降结果，结果如图5所示．计算结果显示，“先下后上”施工，下线引发沉降占比34.1%，上线占比65.9%；“先上后下”施工，下线引发沉降占比仅16.6%，上线占比83.4%．“先下后上”施工总沉降量大于“先上后下”施工．

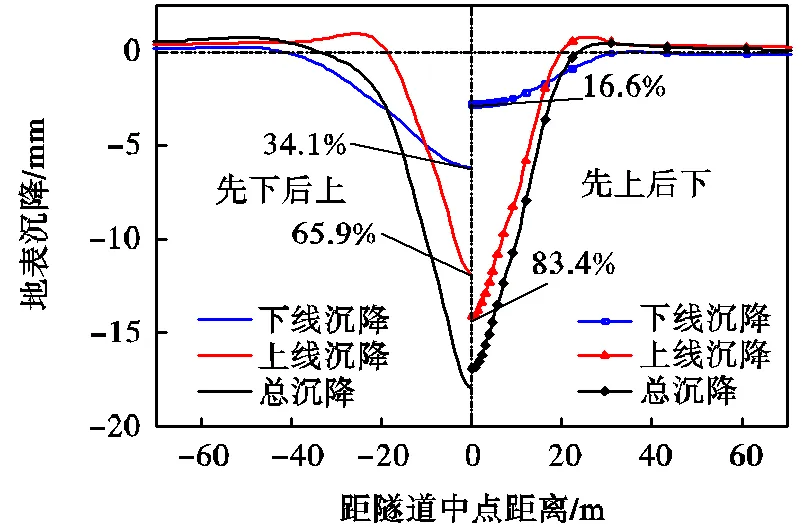
图5 两种施工顺序地表沉降对比

4 施工顺序分析

4.1 参数定义

以往研究中对比不同施工顺序引起的地表沉降时，直接对比“先下后上”和“先上后下”两种施工顺序引起的总沉降大小，这种方法较为直观，但是不利于对该问题展开规律分析．因此，为了深入研究重叠隧道不同施工顺序对土体沉降的影响，本节对相关参数做出如下定义，见图6．图6中，D为下线隧道作为单线隧道施工时引发的土体沉降，D, UD为重叠隧道“先上后下”施工时下线隧道引发的土体沉降．重叠隧道先建隧道会减少后建隧道引发的土体沉降[3]，因此定义DD为上述两种不同工况时下线隧道引发最大沉降改变量，即

图6 重叠隧道施工顺序参数定义

DD＝D－D, UD(3)

同理，可以定义DU为上线隧道作为单线隧道和后建隧道时引发的最大沉降改变量．U为下线隧道作为单线隧道施工时引发的土体沉降，U, DU为重叠隧道“先下后上”施工时上线隧道引发的土体沉降．

DU＝U－U, DU(4)

“先下后上”和“先上后下”两种施工顺序引发的沉降值差值可以由下式计算，其中D＋U, DU为先下后上地表累计沉降，U＋D, UD为先上后下地表累计沉降．

(D＋U,DU)－(U＋D, UD)=(D－D, UD)－

(U－U, DU)=ΔD－ΔU(5)

由以上可知，重叠隧道不同施工顺序地表沉降差值等于ΔD和ΔU的差值，即不同施工顺序时地表沉降大小对比，取决于先建隧道对后建隧道的影响程度.

4.2 施工参数的影响

在已有研究中，已经明确了先建隧道结构存在会明显影响后建隧道施工造成的土体应力变化．在马少坤等[4-5]关于重叠隧道的研究中，也提到了既有隧道的“遮拦”效应．因此本节研究了隧道刚度对重叠隧道不同顺序施工土体沉降结果的影响．定义隧道管片刚度系数如下：

p＝(6)

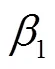
隧道刚度变化对后建隧道最大沉降改变量的影响如图7(a)所示，随着隧道管片刚度增加，先建隧道造成的后建隧道最大沉降改变量Δ逐渐减小，“先下后上”和“先上后下”两种施工顺序中，管片刚度对Δ的影响规律基本一致．“先下后上”施工中的ΔU与“先上后下”施工中的ΔD相比始终较大，差值约为1mm．由于隧道管片刚度变化时，上下线隧道作为单线隧道开挖时引起的土体沉降也将发生变化，因此为了直观地表述由于隧道管片刚度变化造成后建隧道引发土体沉降改变的程度，图7(b)给出了管片刚度系数与后建隧道最大沉降量改变比的关系．在管片刚度在0.1～2.0的范围内时，下线隧道作为后建隧道最大沉降量改变比55%＜DD/D＜57.1%，而上线隧道作为后建隧道，最大沉降量改变比10.1%＜DU/U＜18.3%．由此可见，重叠隧道施工，先修建上线隧道对后建隧道引发沉降的影响比先修建下线隧道的影响要大得多．同时也可以发现，下线隧道作为后建隧道最大沉降改变比随隧道刚度增大而增大，而上线隧道作为后建隧道最大沉降量改变比随隧道刚度增大而减小．

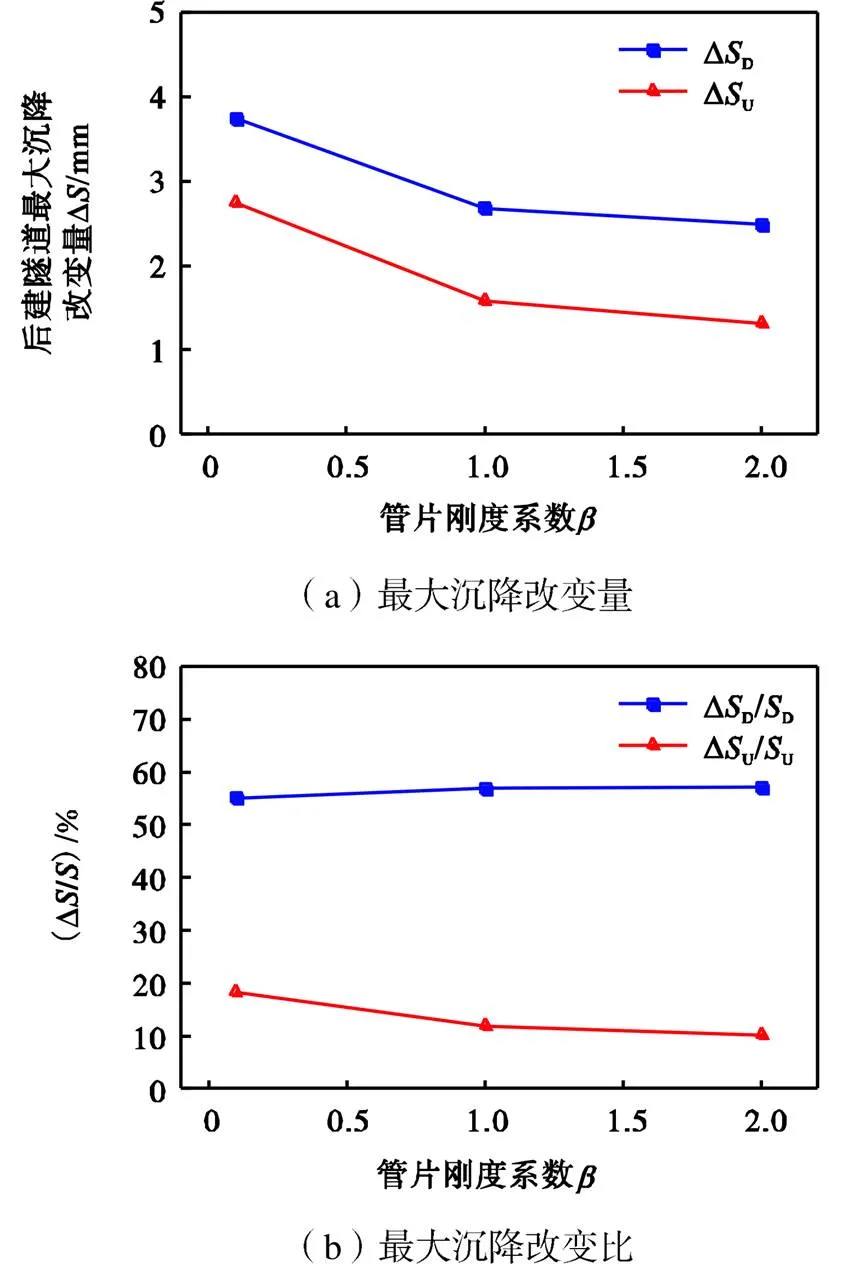
图7 隧道刚度对后建隧道沉降改变的影响

Avgerinos等[21]进行交叠隧道中新建隧道对既有隧道影响的研究中，发现新建隧道的掌子面压力增大对既有隧道有益．因此本节计算掌子面压力变化对不同施工顺序土体沉降的影响．本节定义掌子面压力系数如下：

f, p＝f(7)

式中：f,p为参数分析时的掌子面压力；为掌子面压力系数；f为实际工程中的掌子面压力．本次分析共计算6组不同掌子面压力，掌子面压力系数分别为：1＝0.7，2＝0.8，3＝0.9，4＝1.0，5＝1.1和6＝1.2．掌子面压力变化对后建隧道最大沉降改变量的影响如图8(a)所示，随着掌子面压力增加，先建隧道造成的后建隧道最大沉降改变量Δ逐渐减小，ΔD和ΔU在＝0.8附近相交．图8(b)给出了掌子面系数与后建隧道最大沉降量改变比的关系．在掌子面系数在0.7～1.2的范围内时，下线隧道作为后建隧道最大沉降量改变比41.5%＜ΔD/D＜69.4%，而上线隧道作为后建隧道，最大沉降量改变比8.3%＜ΔU/U＜17.7%．后建隧道最大沉降改变比随着掌子面压力增大而增大，同时下线隧道作为后建隧道时，其最大沉降改变比受掌子面压力变化影响更加明显．

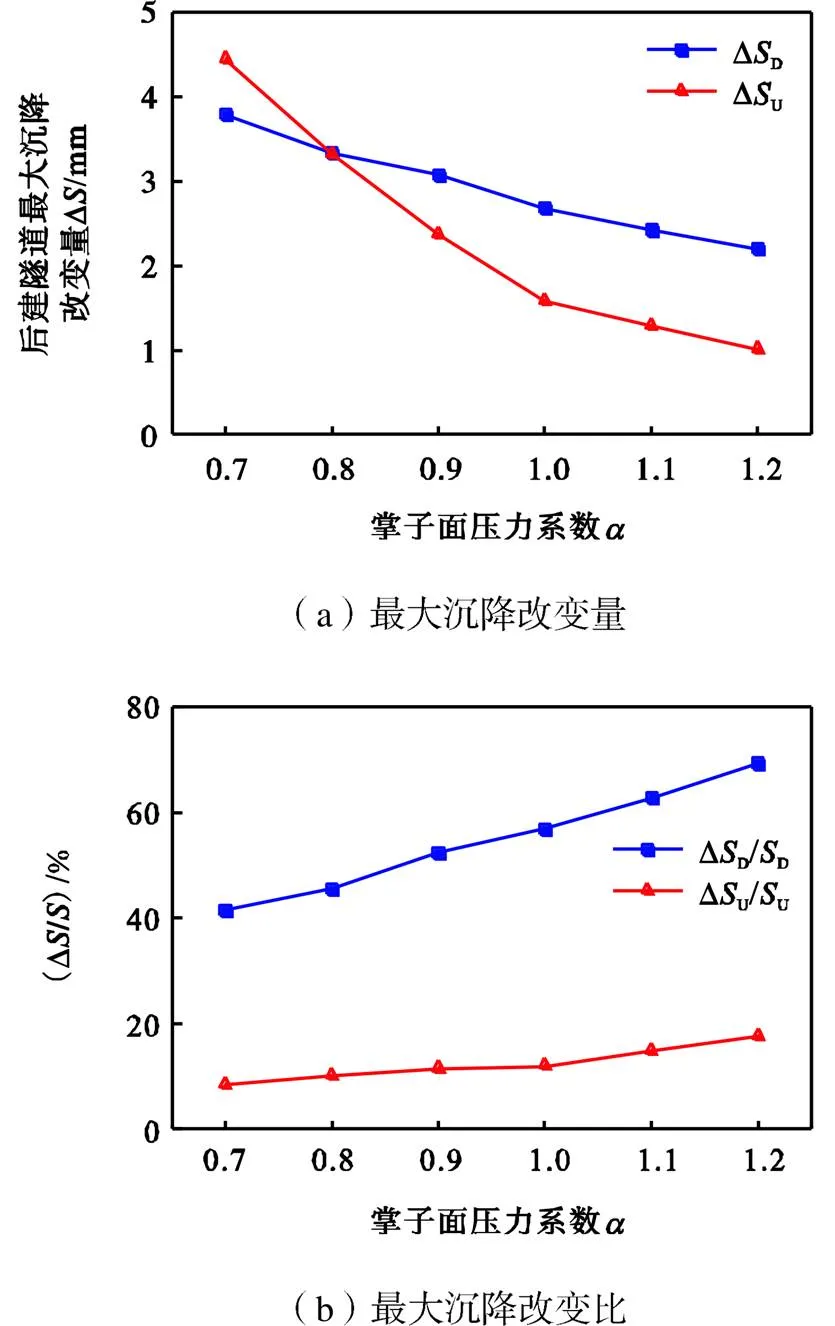
图8 掌子面压力对后建隧道沉降改变的影响

进行参数分析时，发现隧道管片的重量变化也会改变“先下后上”和“先上后下”土体沉降的大小关系．其中管片重量系数定义如下：

p＝(8)

式中：p为参数分析时的管片重量；为管片重量系数；为实际工程中的管片重量．本次分析共计算3组不同管片重量，管片重量系数分别为：＝1，＝0.8和＝2．

图9(a)为管片重量系数与后建隧道最大沉降改变量的关系．随着管片重量增加，下线隧道作为后建隧道最大沉降改变量ΔD逐渐减小，而上线隧道作为后建隧道时，其最大沉降改变量ΔU逐渐增大．ΔD和ΔU在略大于2的位置相交．图9(b)给出了管片重量系数与后建隧道最大沉降量改变比的关系．在管片重量系数在1～3的范围内时，下线隧道作为后建隧道最大沉降量改变比16.1%＜ΔD/D＜60%，受管片重量系数影响明显；而上线隧道作为后建隧道，最大沉降量改变比11.2%＜ΔU/U＜11.9%，几乎不受到管片重量系数变化的影响．同时，后建隧道最大沉降改变比随着管片重量系数增大而增大．

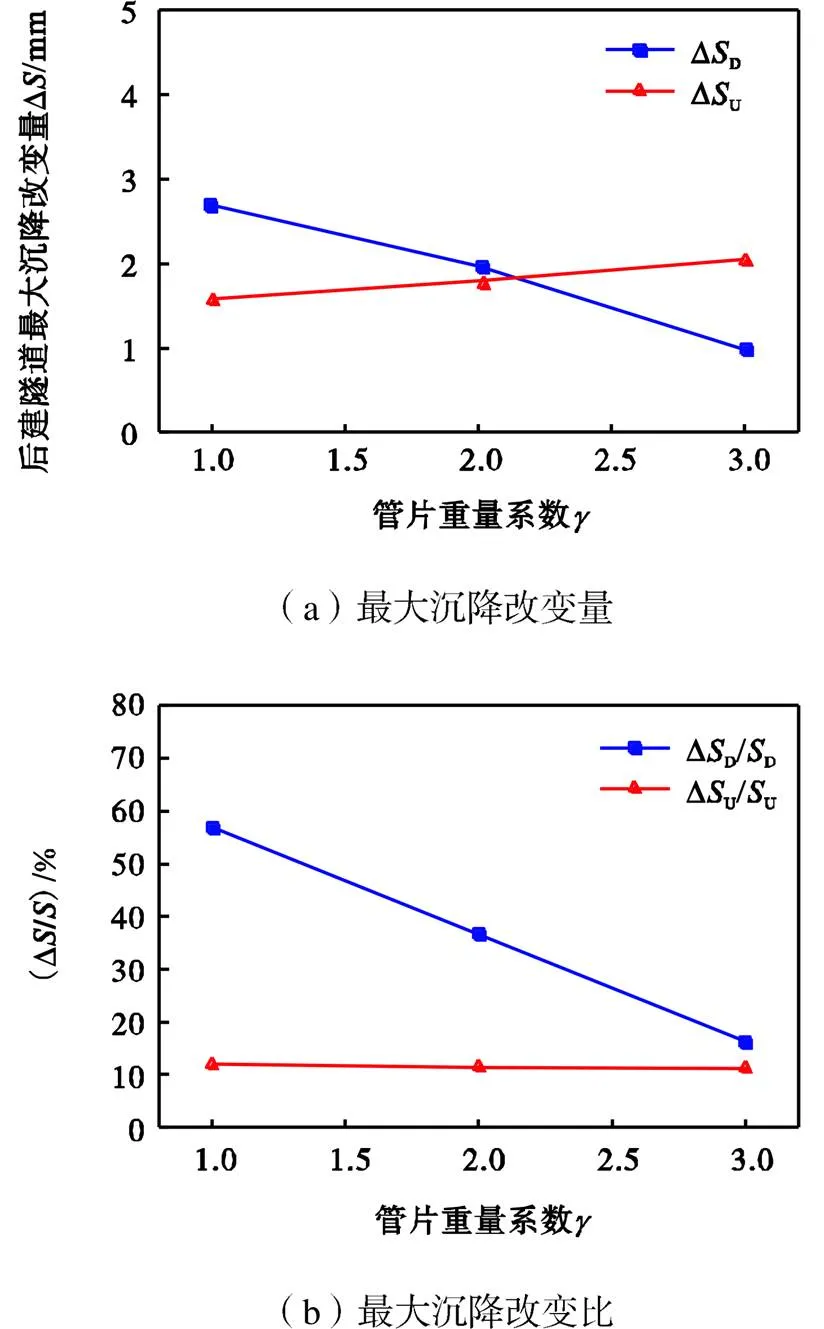
图9 管片重量对后建隧道沉降改变的影响

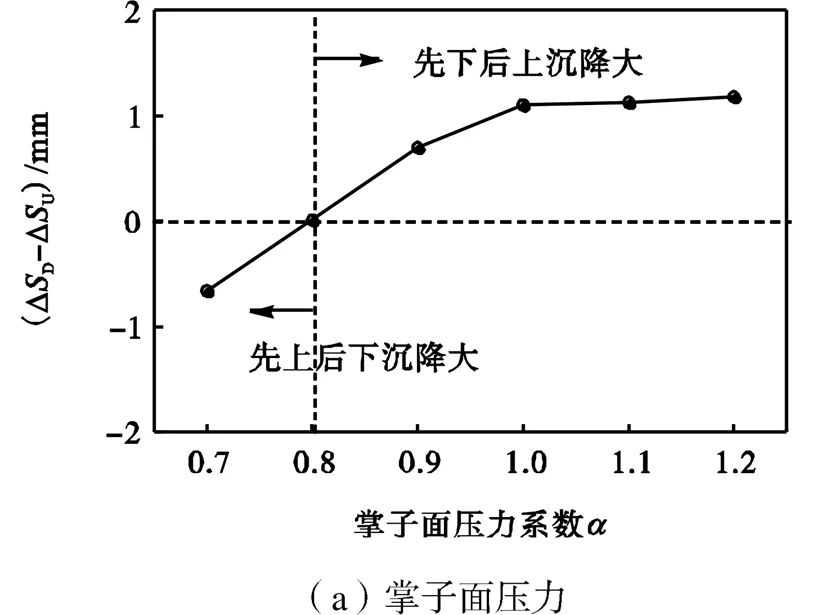
图10为不同施工参数变化对重叠隧道不同施工顺序引发沉降大小关系的影响．隧道管片刚度变化时，“先下后上”施工引发的总沉降始终比“先上后下”大约1mm．因此尽管上文中已指出先建隧道的结构的“遮拦”效应会明显影响后建隧道施工引发的土体应力变化，但隧道结构的刚度并不会定性地改变两种施工顺序土体沉降大小的关系．掌子面压力较小时(＜0.8)，“先下后上”施工引发的总沉降比“先上后下”小；当掌子面压力增加时(＞0.8)，两种施工顺序总沉降值大小关系发生反转，“先下后上”施工引发的总沉降比“先上后下”大．管片重量增加时，也会出现“先下后上”施工总沉降从比“先上后下”大到比“先上后下”小的转变．

5 施工间隔分析

5.1 施工间隔定义

重叠隧道施工间隔及其参数的定义如图11所示，其中为盾构长度(数值分析中＝8.4m)，g为上下线隧道盾构机同步施工时二者掌子面之间的距离．本节共计算13个不同的施工间隔方案(-15～＋15)，其中g＞0为下线隧道先掘进，g＜0时为上线隧道先掘进，g＝0时为上下线隧道盾构机并行掘进．

5.2 施工间隔对地表变形的影响

不同施工间隔土体沉降计算结果如图12所示．其中图12(a)为不同盾构施工间隔时地表最大沉降值，地表最大沉降值为重叠隧道施工完成时隧道中心正上方的地表沉降．图12(b)为不同盾构掘进间隔对应的地表最大沉降发展速率，地表最大沉降发展速率计算方法为

式中：为最大沉降发展速率；S为地表最大沉降值；t为施工时间．

图12中，下线隧道先行掘进时地表最大沉降值总大于上线隧道先行掘进，而下线隧道先行掘进时沉降发展速率则较上线隧道先行掘进更慢．施工间隔在0～3的范围内时，不同施工间隔土体沉降数据变化较大，这是由于该距离范围内先行掘进的盾构机尾部注浆与后掘进盾构机掌子面开挖相近，施工扰动相互作用较为复杂．当掘进间隔大于5时，土体沉降数据变化较小．

5.3 施工间隔对隧道变形的影响

不同施工间隔上下线隧道竖向位移计算结果如图13所示，图中(a)与(b)分别为上线隧道和下线隧道的竖向位移情况．其中隧道竖向位移为管片安装完成后至重叠隧道施工完成时隧道截面中心点产生的竖向位移．可以看出，不同施工间隔情况下，上下线隧道施工完成后都会出现一定的上浮，这是由于土体开挖卸荷和孔隙水浮力作用．但当上线隧道先行掘进时，其下方掘进的下线盾构开挖卸荷会抵消该效应，因此当上线隧道先开挖且盾构掘进间隔大于时，上线隧道的竖向位移很小，接近于0．上下线盾构掘进间隔大于时，对两条隧道竖向位移值影响均较小．

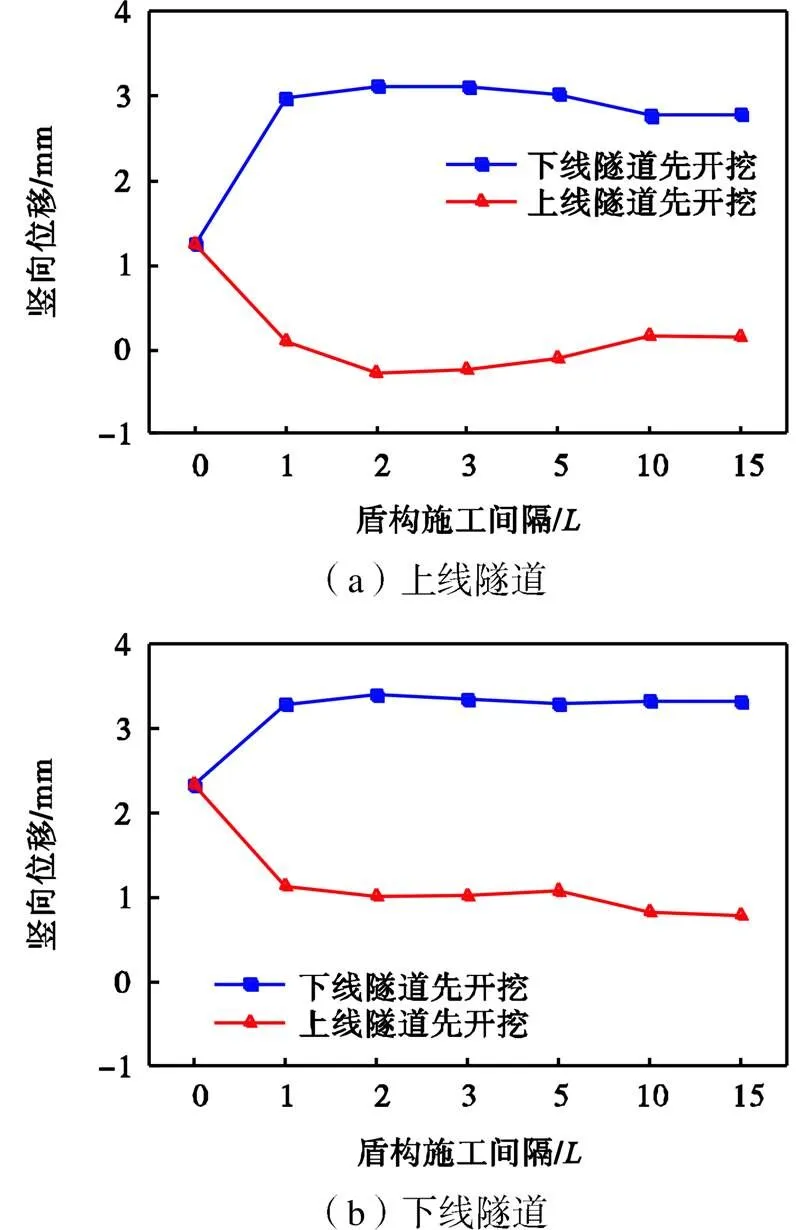
图13 施工间隔对隧道竖向位移的影响

不同施工间隔上下线隧道收敛变形计算结果如图14所示，图中(a)与(b)分别为上线隧道和下线隧道的隧道收敛情况．其中，隧道收敛变形是指隧道拱顶位移与拱底位移的差值，表示隧道截面竖向直径变化的情况，其值为负表示隧道自安装完成至重叠隧道施工完成过程中竖向直径变小，即隧道截面被“压扁”．下线隧道由于埋深较深，土压力较大，隧道变形较大，其中上线隧道先开挖的情况隧道收敛大于下线隧道先开挖的情况．

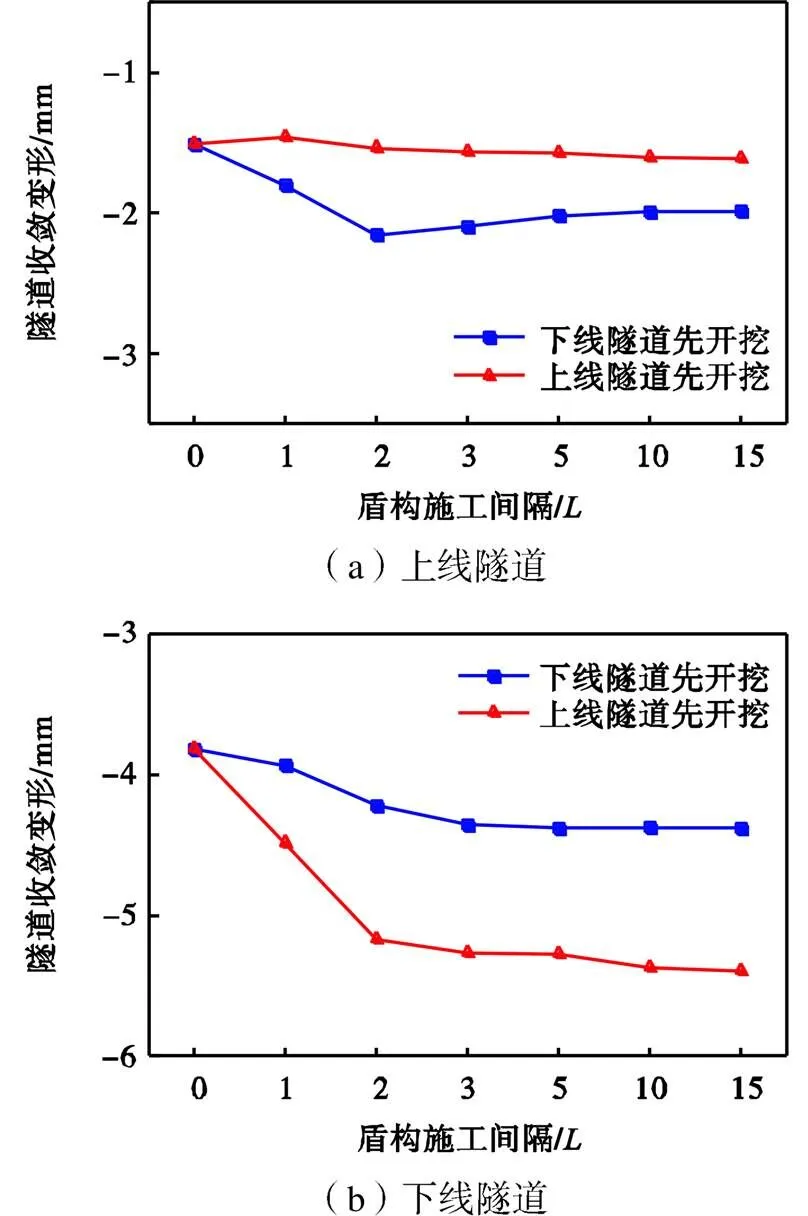
图14 施工间隔对隧道收敛的影响

5.4 基于相对差距和法的施工间隔方案评价

本节共分析13个施工间隔方案，不同施工间隔方案评价指标较多时，很难直观评价不同施工间隔方案的优劣．因此，本小节使用相对差距和法，对不同施工间隔方案进行比较．

相对差距和法较为适用于多评价指标的不同方案评价，其具体原理如下．

设有个参评方案，各有项评价指标，则每一方案的指标数据为

＝(1j，2j，…，)＝1，2，3，…，

设最优样本为0＝(1，2，…，，…，)，最优样本0中的各元素按如下方法确定：对于高优指标，＝max{1，2，…，，…，}，即所有个样本中第项指标的最大者；对于低优指标，＝min{1，2，…，，…，}，即所有个样本中第项指标的最小者．各样本与最优样本的加权相对差距和为

式中：为第项指标的权重系数；为所有样本的第项指标值的中位数．按值的大小对个样本依次排序，值越小样本越接近最优水平．

对于本节分析的不同施工间隔方案的评价，其中关键问题为各评价指标的权重系数的确定．如果以评价指标重要性为依据确定权重系数，较难找到可靠参考且过于主观．因此，参考现行规范对不同指标控制值范围，确定指标权重系数，即

式中：为所有样本的第项指标值的中位数；r为规范中对应指标的控制极限值．

评价指标为地表沉降最大值、沉降发展速率、隧道竖向位移和隧道收敛变形．表5为现行规范《GB 50911—2013城市轨道交通工程监测技术规范》对上述监测指标控制值的规定．

表5 规范控制值

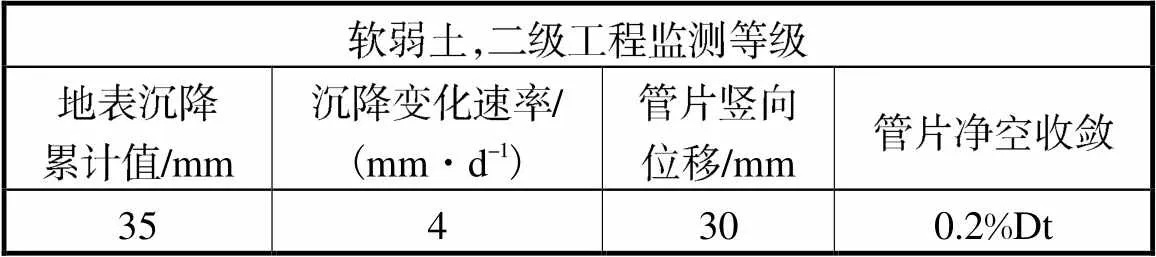
Tab.5 Control limits in the regulation

根据以上方法，计算可得不同施工间隔方案值如表6所示．其中值最优解为-2，即上线盾构机先出发，下线盾构机在距其2距离同步掘进．但考虑实际施工情况，两盾构机相距0～3时，后盾构机掌子面与前盾构机盾尾注浆和二次注浆作业位置过于接近，未凝固的浆液易窜入后盾构机土仓，极大地提高盾构隧道施工的风险性，因此不建议盾构机间距小于5同步掘进．计算结果中-5与＋10得到的值基本相同，综合考虑已有重叠隧道工程施工顺序惯例(“先下后上”为主)与“先下后上”隧道受力较优的研究结论，下线盾构先掘进，上线盾构在其后距10位置同步掘进，为重叠隧道同步施工最佳施工间隔.

表6 施工间隔方案评价结果

Tab.6 Evaluation results of construction lagging distance

6 结论

本文采用数值模拟方法对重叠隧道施工中上下线隧道施工顺序和同步施工时施工间隔的影响展开研究，得到的主要结论如下．

(1) 重叠隧道施工顺序中，对于“先下后上”和“先上后下”引发土体沉降大小比较的问题，得到了不同的结论．本文计算结果发现重叠隧道“先下后上”和“先上后下”施工引起土体沉降大小比较取决于先建隧道对后建隧道引发沉降的影响程度，掌子面压力和隧道重量变化会改变不同施工顺序引发地表沉降的大小关系，为解释已有研究分歧提供一个新的角度，优化了已有研究的简单定性结论．

(2) 上线隧道作为后建隧道时，受下线隧道影响较小，其最大沉降改变比最大约20%；而下线隧道作为后建隧道时，受上线隧道影响较大，其最大沉降改变比最大约70%．

(3) 掌子面压力和隧道重量变化会改变“先下后上”和“先上后下”引发土体沉降大小关系．掌子面压力增大时，“先下后上”地表沉降从比“先上后下”小变为比“先上后下”大；管片重量增大时，“先下后上”地表沉降从比“先上后下”大变为比“先上后下”小．

(4) 本文计算分析了重叠隧道同步施工不同施工间隔对地表最大沉降、沉降速率、隧道竖向位移和隧道收敛变形的影响．基于相对差距和法，本章对不同施工间隔的施工效果进行评价，结合盾构隧道施工实际综合考虑，推荐最优施工间隔为10，即下线盾构机先出发，上线盾构机后出发，两者间距10倍盾构长度，应用该方案可减少近一半重叠隧道施工工期.

［1］ Addenbrooke T I，Potts D M. Twin tunnel interaction：Surface and subsurface effects[J]. International Journal of Geomechanics，2001，1(2)：249-271.

［2］ Chehade F H，Shahrour I. Numerical analysis of the interaction between twin-tunnels：Influence of the rela-tive position and construction procedure[J]. Tunnel-ling and Underground Space Technology，2008，23(2)：210-214.

［3］ Do N A，Dias D，Oreste P. Three-dimensional numeri-cal simulation of mechanized twin stacked tunnels in soft ground[J]. Journal of Zhejiang University Science A，2014，15(11)：896-913.

［4］ Ma S K，Liu Y，Lü X L，et al. Settlement and load transfer mechanism of pipeline due to twin stacked tun-neling with different construction sequences[J]. KSCE Journal of Civil Engineering，2018，22(10)：3810-3817.

［5］ 马少坤，刘 莹，邵 羽，等. 盾构双隧道不同开挖顺序及不同布置形式对管线的影响研究[J]. 岩土工程学报，2018，40(4)：689-697.

Ma Shaokun，Liu Ying，Shao Yu，et al. Effects of twin shield tunneling with different construction sequences and different relative locations on adjacent pipelines[J]. Chinese Journal of Geotechnical Engineering，2018，40(4)：689-697(in Chinese).

［6］ 郭 晨. 近距离重叠盾构隧道施工影响的数值模拟[D]. 成都：西南交通大学，2009.

Guo Chen. Numerical Simulation of Influence of Shield Tunneling in Closely Overlapped Tunnel[D]. Chengdu：Southwest Jiaotong University，2009(in Chinese).

［7］ 金乃麒，徐剑旋，高跃峰. 地铁叠线隧道小净距盾构施工工序研究[J]. 山西建筑，2021，47(6)：147-148.

Jin Nailin，Xu Jianxuan，Gao Yuefeng. Study on con-struction sequence in close range overlapped tunnel con-struction[J]. Shanxi Architecture，2021，47(6)：147-148(in Chinese).

［8］ 陈 平. 重叠地铁区间隧道TBM施工的数值模拟[D]. 兰州：兰州交通大学，2011.

Chen Ping. The Numerical Simulation of TBM Adjacent Tunnel Construction about Overlapped Subway[D]. Lanzhou：Lanzhou Jiaotong University，2011(in Chi-nese).

［9］ 范晓真，骆 祎，王伊丽，等. 小净距上下重叠盾构隧道施工扰动数值分析[J]. 科学技术与工程，2017，17(11)：108-114.

Fan Xiaozhen，Luo Yi，Wang Yili，et al. Numerical study on close range overlapped tunneling[J]. Science Technology and Engineering，2017，17(11)：108-114 (in Chinese).

［10］ 江 宇，王士民，王 鹰，等. 近距离重叠盾构隧道施工工序优化[J]. 施工技术，2015，44(13)：92-96.

Jiang Yu，Wang Shimin，Wang Ying，et al. Process optimization of close overlapping shield tunnel during construction[J]. Construction Technology，2015，44(13)：92-96(in Chinese).

［11］ Do N A，Dias D，Oreste P. 3D numerical investigation of mechanized twin tunnels in soft ground-Influence of lagging distance between two tunnel faces[J]. Engineer-ing Structures，2016，109：117-125.

［12］ Franzius J N，Potts D M. Influence of mesh geometry on three-dimensional finite-element analysis of tunnel excavation[J]. International Journal of Geomechanics，2005，5(3)：256-266.

［13］ Wongsaroj J，Soga K，Mair R J. Modelling of long-term ground response to tunnelling under St James’s Park，London[J]. Geotechnique，2007，57(1)：75-90.

［14］ Zheng G，Zhang T，Diao Y. Mechanism and counter-measures of preceding tunnel distortion induced by suc-ceeding EPBS tunnelling in close proximity[J]. Com-puters and Geotechnics，2015，66：53-65.

［15］ Zheng G，Lu P，Diao Y. Advance speed-based paramet-ric study of greenfield deformation induced by EPBM tunneling in soft ground[J]. Computers and Geotech-nics，2015，65：220-232.

［16］ Lee K M，Ge X W. The equivalence of a jointed shield-driven tunnel lining to a continuous ring structure[J]. Canadian Geotechnical Journal，2001，38(3)：461-483.

［17］ Shiba Y，Kawashima K，Obinata N，et al. An evaluation method of longitudinal stiffness of shield tunnel linings for application to seismic response analyses[J]. Doboku Gakkai Ronbunshu，1988，1988(398)：319-327.

［18］ Kasper T，Meschke G. A 3D finite element simulation model for TBM tunnelling in soft ground[J]. Interna-tional Journal for Numerical and Analytical Methods in Geomechanics，2004，28(14)：1441-1460.

［19］ Kasper T，Meschke G. On the influence of face pressure，grouting pressure and TBM design in soft ground tunnelling[J]. Tunnelling and Underground Space Technology，2006，21(2)：160-171.

［20］ Meschke G，Kropik C，Mang H A. Numerical analyses of tunnel linings by means of a viscoplastic material model for shotcrete[J]. International Journal for Numerical Methods in Engineering，1996，39(18)：3145-3162.

［21］ Avgerinos V，Potts D M，Standing J R. Numerical investigation of the effects of tunnelling on existing tunnels[J]. Géotechnique，2017，67(9)：808-822.

Influence of Construction Sequence and Lagging Distance on Ground Movements Induced by Two Overlapping Shield Tunnels

Fan Qi，Zhang Tianqi

(School of Civil Engineering，Tianjin University，Tianjin 300350，China)

The urban underground space in China has become increasingly crowded due to underground construction projects. Because of the space constraints in a narrow underground environment，urban subway twin tunnels must occasionally be constructed as overlapping tunnels. Since the soil deformation caused by the construction has a superimposing effect because of the overlapping arrangement of tunnels，the surface settlement caused by the construction of overlapping tunnels is difficult to control and predict. Moreover，since overlapping tunnels are designed to fit into narrow spaces，they are usually constructed near other structures，such as building foundations，pipes and other tunnels. In this study，a detailed finite element method simulation model is proposed based on the construction of overlapping tunnels for Tianjin Metro Line 5. Construction parameters such as face support，shield friction，shield thrust，tail grouting，and trailer weight were considered in the simulation. The calculation results of the proposed model were compared and verified with the measured data，demonstrating the reliability of the numerical model. In this study，ground settlements due to tunneling were investigated using different construction sequences of overlapping tunnels and the construction parameters of shield tunnels. Simple qualitative conclusions derived from existing studies were perfected. Various lagging distances during the simultaneous construction of overlapping tunnels were evaluated，and the surface settlement，settling rate，tunnel displacement，and tunnel convergence were analyzed. Moreover，a construction plan was proposed using a statistical method and construction conditions. The results can aid in reducing the construction time limit cost of overlapping tunnels by 50%.

overlapping tunnels；construction sequence；lagging distance；field measurement

10.11784/tdxbz202111001

TU43

A

0493-2137(2022)12-1318-11

2021-11-01；

2021-12-03.

范 奇（1991—  ），男，博士研究生.

范 奇，fanqi@tju.edu.cn.

国家自然科学基金青年科学基金资助项目(51808387).

Supported by the Youth Science Fund Project of National Natural Science Foundation of China(No. 51808387).

(责任编辑：樊素英)