用户侧分布式储能参与一次调频的日内前瞻-值函数近似策略

2022-10-31温可瑞李卫东王海霞

电力系统自动化 2022年20期

温可瑞，李卫东，孙乔，巴宇，王海霞

（1. 大连理工大学电气工程学院，辽宁省大连市 116024；2. 国网辽宁省电力有限公司大连供电公司，辽宁省大连市 116001）

0 引言

随着电力市场机制的建立健全以及储能技术性能的快速提升，用户侧分布式储能（distributed energy storage，DES）的并网装机规模显著增长［1-3］。若考虑在电价响应的基础上，以聚合商模式整合汇聚容量较小、分散布局的用户侧DES 参与一次调频（primary frequency regulation，PFR）辅助服务［4-6］，有利于挖掘其潜在的技术经济价值［7］。但随着DES应用目标拓展，其运行控制过程愈发复杂。

聚合商在日前参与PFR 市场投标并确定出清结果后，日内需要优化决策各时段DES 的功率基线及PFR 备用功率，在保障频率响应能力的同时最大化整体经济效益［8-9］。然而，由于负荷、电价及频率信息具有不确定性，当前决策结果对后续过程的技术经济影响难以精准辨识，从而给日内优化运行带来了挑战［10］。因此，亟须对不确定信息下用户侧DES 的日内运行策略进行合理设计。

近年来，基于在线凸规划［11-12］、Lyapunov 优化［13］和在线直接前瞻（direct lookahead，DLA）［14-15］（亦称模型预测控制）的日内运行策略相继被提出。其中，在线凸规划将目标函数表示为决策变量的凸函数，通过在线求解凸规划问题获取实时决策。Lyapunov 优化通过建立Lyapunov 函数并最小化其偏移量，在兼顾系统稳定性的前提下开展运行优化决策。上述方法均不依赖未来预测信息，且不强调决策过程的全局最优解，而是在长时间视角下确保系统处于满意的运行状态。

相比于以上方法，DLA 基于滚动更新的超短期预测数据获取实时决策，虽然能够满足调频性能及求解时限要求，但其局部优化特征难以覆盖全局运行效益［16］。为了克服DLA 局部时域的不足，可以考虑随机前瞻（stochastic lookahead，SLA）策略［17-18］。SLA 策略充分结合日前及日内预测信息，在线求解两阶段随机规划模型，计及随机阶段可扩展优化时域、提升运行效益，但会导致求解规模急剧增长、运算开销激增。因此，如何有效兼顾全局优化性能与在线运算开销仍是当前策略设计的难点。此外，已有研究中通常依据PFR 备用容量保守设置荷电状态（state of charge，SOC）约束［14，19］，尽管能够保障DES 的频率调节裕度，但亦造成电量空间资源浪费。

鉴于上述不足，本文将日内运行问题构建为恰当考虑PFR 性能约束的马尔可夫决策过程（Markov decision process，MDP），进而提出一种“前瞻 - 值函数近似（lookahead-value function approximation，LVFA）”混合运行策略。结合滚动更新的预测信息以及离线训练的长期时域近似效益函数，通过在线求解两阶段近似动态规划（twostage approximate dynamic programming，TSADP）模型以获取各时段的近似最优决策。通过算例分析对所提策略的离线训练效果及日内运行性能进行了验证。

1 问题描述与建模

1.1 问题描述

目前，多数电力发达的国家和地区建立了相对完善的电力市场体系，不同市场架构及交易模式有所差异。用户侧的典型电价机制包括尖峰电价、分时电价和实时电价，本文即在波动较大的实时电价模式下开展研究。此外，PFR 服务正处于发展阶段，不同市场环境下的PFR 规则有所区别，相关机制的共性特征［20-21］可归纳如下。

1）投标要求:PFR 供应商的投标容量应满足市场规定的最低投标容量限制。

2）技术响应:采用下垂控制，即自动线性响应本地频率偏差提供实时调频功率。

3）补偿收益:供应商依据出清价格、中标容量与服务时长三者的乘积获取补偿收益。

4）失效惩罚:供应商提供PFR 服务的失效率应低于最大允许值，否则依据调频效果进行惩罚。为了规避调频失效带来的惩罚风险，供应商通常会严格限制自身的PFR 失效率。

基于上述市场机制，聚合商通过集中协调用户侧DES，在响应实时电价的基础上参与PFR 服务，按照时间维度可划分为日前投标、日内运行及实时控制3 个环节，基本流程如图1 所示。

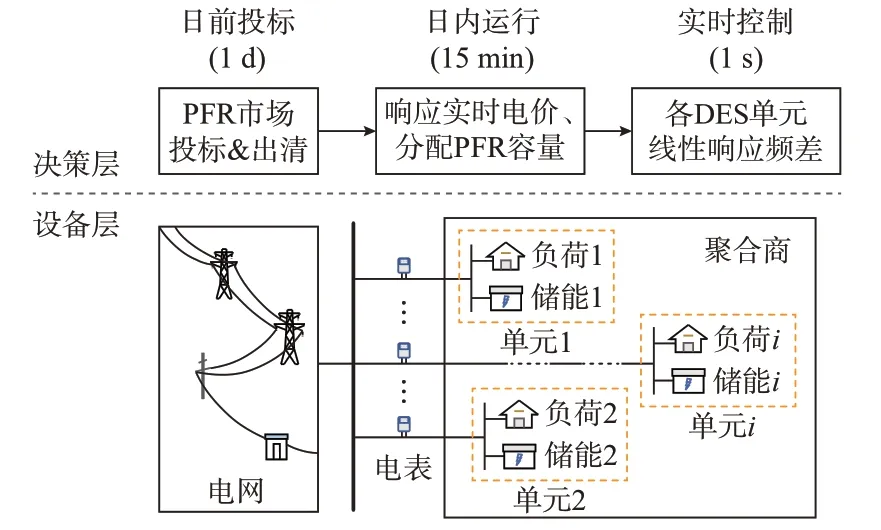
图1 用户侧DES 提供双重服务的基本流程Fig.1 Basic flowchart of dual services provided by user-side DES

在上述流程中，日内优化运行属于承上启下的关键环节，优化决策结果对于DES 的技术经济效益影响显著。因此，本文在市场出清完成，即已知聚合商PFR 中标容量及出清价格后，针对日内运行过程中各时段动态优化决策问题开展研究。

1.2 不确定环境下的日内运行MDP 模型

日内运行问题的核心是通过优化各时段各单元DES 的功率基线及PFR 备用功率，在保障PFR 响应能力的同时，最大化所辖全部DES 的经济效益。由于负荷、电价及频率信息具有不确定性，需要结合获取的信息开展动态优化决策。换而言之，日内运行属于不确定环境下的序贯决策过程。

为了对上述问题特征进行建模，本文将其描述为MDP 模型。MDP 作为随机序贯决策问题的通用模型［22］，通过对运行时域的离散化处理和对状态、决策变量、外部信息、转移函数以及目标函数等要素的刻画，能够反映不确定环境下动态决策过程的时序演进、状态转移及效益累积等特征。

将聚合商协调的DES 划分为I个单元，并定义单元集合Iset={1，2，…，i，…，I}。以Δt为时间粒度，对日内运行的时域范围T进行离散化处理，并定义时刻集合Tset={0，Δt，2Δt，…，t，…，T}。

1.2.1 状态变量

为了表征日内运行过程中各单元DES 当前的状态以及全部必要的环境信息，在MDP 框架下采用状态变量对其进行建模。本文状态变量St为:

1.2.2 决策变量

在决策过程中应严格满足如下约束条件。

1）有功功率平衡约束

由图1 可知，聚合商所辖全部负荷、DES 与电网的实时交互功率满足有功功率平衡。选取自电网注入功率的方向作为正方向，则有:

式中:Λ{z}为条件指示函数，当z为真时，函数值取1，反之取0；Δfmax为线性响应的最大频率偏差。

2）PFR 中标容量约束

为了规避调频失效带来的惩罚风险，本文要求聚合商严格保障PFR 可靠性。整体而言，各单元PFR 备用功率之和应满足中标容量值，即

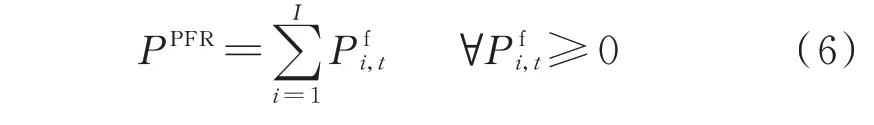
式中:PPFR为聚合商在PFR 市场的中标容量。

13.对于经产母猪的诱导发情，断奶后7 d内，肌注“氯前列烯醇（PG）”0.2 ml，再肌注“孕马血清（PMSG）”1 000单位。

3）考虑PFR 的单元功率约束

各单元DES 的功率基线与PFR 备用功率之和应限制在额定功率上下限范围内，表示为:

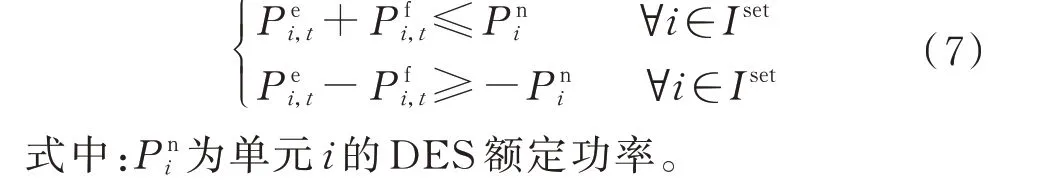
4）考虑PFR 的单元SOC 约束

1.2.3 外部信息

外部信息用于对日内运行过程中不确定信息预测值与真实值的误差建模，其可表示为:

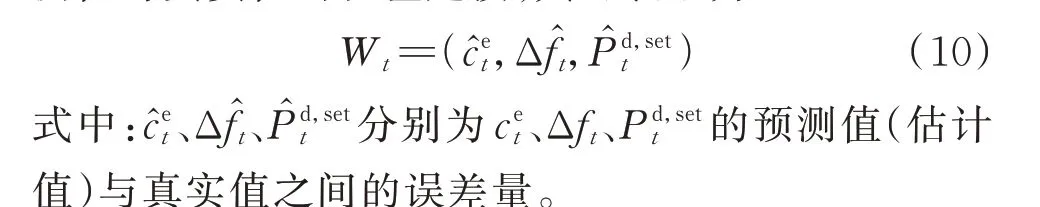
基于以上定义，日内运行过程可以用时序演进的状态、决策及外部信息描述，其轨迹可表示为:

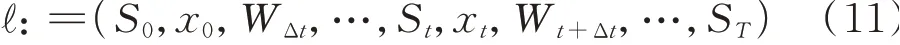
1.2.4 转移函数

转移函数是指系统根据决策xt及外部信息Wt+Δt，由当前状态St转移到下一时刻状态St+Δt的过程。本文可定义转移函数为:

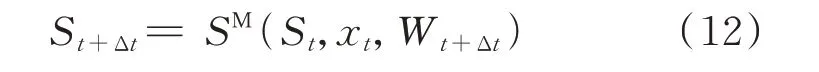
式中:SM(·)为转移函数，包括各状态变量的动态转移，具体可分为储能SOC 和环境信息的转移过程。

1）储能SOC 的转移过程

伴随日内充放电过程，各单元DES 从t时刻至t+Δt时刻的SOC 动态转移可描述为:

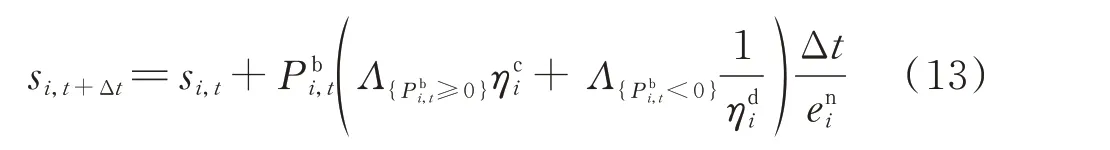
2）环境信息的转移过程

电价、负荷及频率偏差的动态转移均属于状态独立的信息过程。考虑到信息的预测值与真实值之间的误差量，转移过程可表示为:

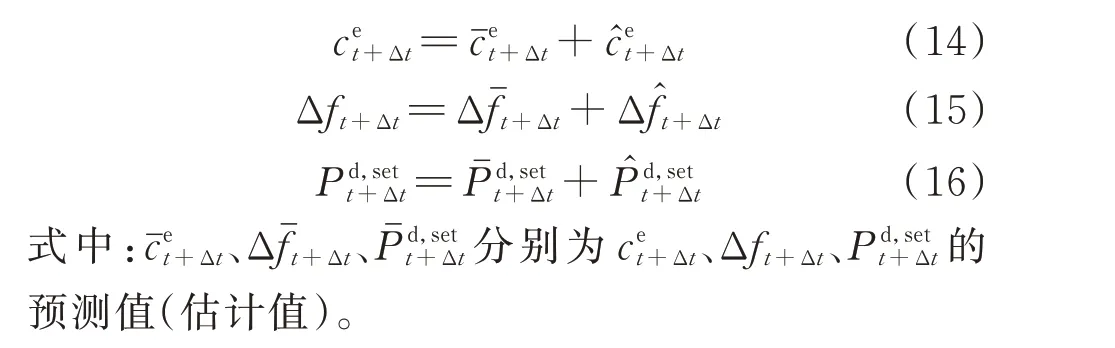
1.2.5 目标函数

对于用户侧DES 提供双重服务的日内运行问题，其目标是在满足相关约束条件下使各时段累计期望净效益最大化。目标函数F*可表示为:

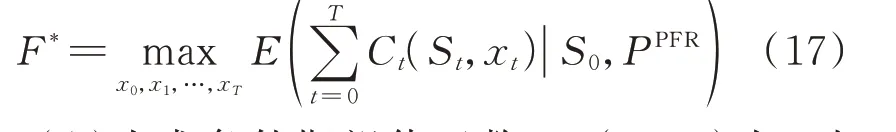
式中:E(·|·)为求条件期望值函数；Ct(St，xt)为t时段的净效益函数，既包括响应电价所降低的购电成本、提供PFR 服务的补偿收益，也要计及运行维护成本。

单个运行时段的净效益Ct可表示为:

2 不确定环境下的日内运行策略

2.1 考虑长期效益函数近似的TSADP 模型

日内MDP 模型从整体上明确了相关变量及动态转移过程，具体到实时优化问题:假设当前时刻为tc，按照滚动更新预测的时域范围将后续时域划分为两阶段，即短期时域和长期时域。

定义1:短期时域表示当前时刻tc至未来时刻tf=tc+HΔt之间的滚动更新预测时域。在短期时域范围HΔt内，电价及负荷的滚动更新预测精度明显高于日前预测结果。

定义2:长期时域表示未来时刻tf至日运行终止时刻T之间的时域范围。对于该时域范围，已知电价及负荷日前预测及其误差分布信息。

尽管相应模型的复杂度较低，适于在线优化求解，但其局部优化时域难以保证全局运行效益。考虑到上述不足，SLA 策略通过综合利用日前及日内预测信息，构建当前时刻tc至终止时刻T的两阶段随机规划模型，表示为:

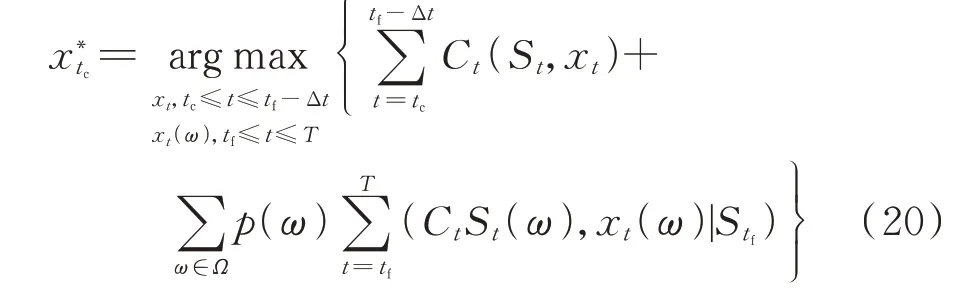
式中:Ω为样本路径集合；ω为随机抽取的样本路径；p(ω)为样本路径ω出现的概率；xt(ω)为样本路径ω的决策变量；St(ω)为样本路径ω下t时刻的状态变量。SLA 能够实现全局优化效果，但过多的样本路径会增大问题规模，致使在线运算开销大幅增加。

综上，现有策略面临的核心问题是难以兼顾全局优化性能与在线运算开销。为此，本文考虑采用“离线计算-在线应用”模式:离线阶段计算各时段状态下的长期时域期望效益；在线阶段直接调用相应的长期效益函数，从而构建实时两阶段优化模型进行决策，其基本原理如图2 所示。一般而言，基于Bellman 原理可将日内运行问题解耦为多个单时段子问题，运用动态规划逆序递归，即可离线计算各时段状态下运行至最终时刻的期望效益。定义最优值函数V*t(St)表示t时刻状态St至最终时刻T的累积期望效益。运用Bellman 方程可将目标函数式（17）递归表示为:

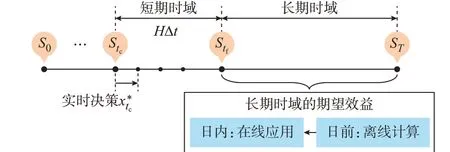
图2 长期期望效益的“离线计算-在线应用”模式Fig.2 “Offline calculation-online application”mode for long-term expected benefit

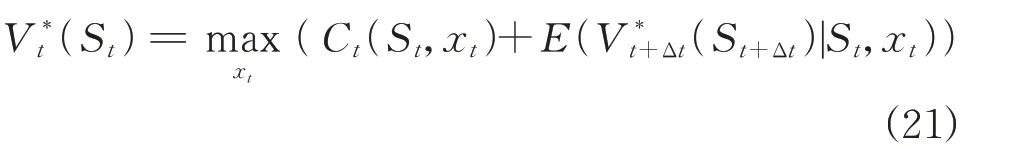
然而，动态规划求解式（21）需要遍历全部可行状态的条件期望E(V*t+Δt(St+Δt)|St，xt)。受制于DES 状态及决策空间离散规模激增所引发的“维数灾”，直接求取全部期望效益存在计算障碍。

为了在离线阶段计算长期期望效益，引入近似动态规划框架下的值函数近似思想。首先，选取恰当类型的值函数近似表征各时段状态下的长期期望效益；然后，采用合适的算法对值函数进行迭代训练，使之逐渐逼近真实期望效益，有效规避遍历计算的“维数灾”。值函数近似的关键在于:1）选取何种类型函数实现长期效益近似；2）如何对近似效益函数开展离线训练。

长期效益函数的近似形式及离线训练将在第3章进行详细叙述。通过离线计算过程可以得到各时段对应的长期效益函数Vˉtf(Stf)为:

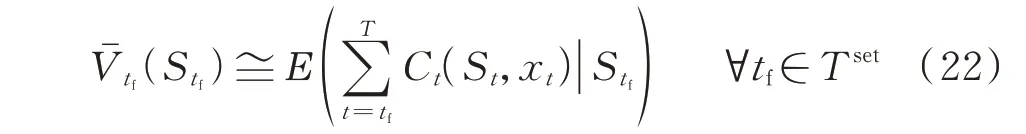
结合滚动更新预测信息及离线近似的长期效益函数，构建当前时刻tc的TSADP 模型，即

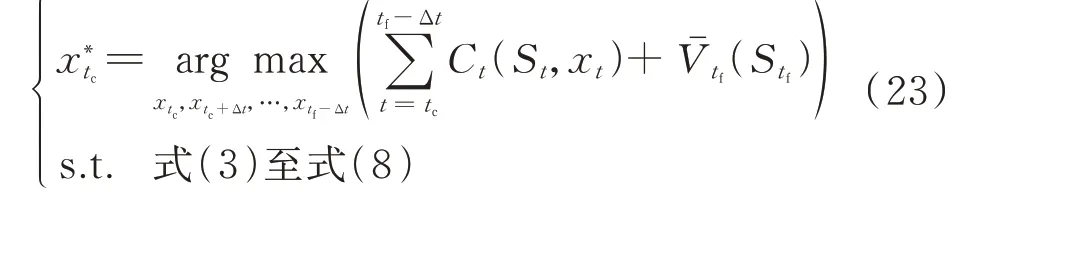
相较于DLA 策略所构建的短期时域优化模型，TSADP 模型能够计及决策对长期时域范围的影响，即考虑全局优化效果。而相较于SLA 策略采用随机抽样方法对长期时域进行建模，TSADP 模型直接调用离线近似的长期效益函数，有效缓解在线优化模型的复杂度，继而降低在线运算开销。

2.2 基于TSADP 的日内运行策略

基于实时TSADP 优化模型，日内运行策略可以归纳为混合前瞻以及值函数近似的策略类型，即LVFA 策略，其原理图如图3 所示。该策略主要由离线阶段和在线阶段两部分组成。

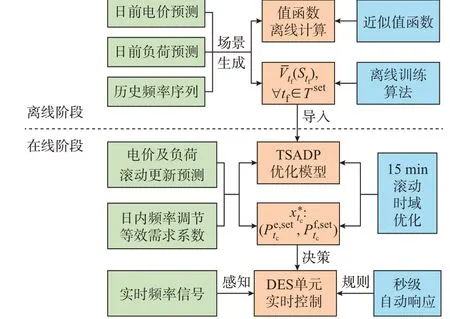
图3 基于TSADP 的LVFA 运行策略Fig.3 TSADP based LVFA operation strategy

离线阶段:基于日前电价、负荷预测信息及历史频率数据生成训练场景，并选取恰当类型的近似值函数及训练算法，离线计算各时段的近似效益函数，以供在线阶段的滚动优化模型调用。

在线阶段:按照时间尺度划分为15 min 滚动时域优化和秒级自动响应2 个功能环节。首先，结合日内电价和负荷的滚动更新预测信息、PFR 等效需求系数以及离线计算的长期效益函数，在线滚动时域求解TSADP 优化模型，即可动态地获取当前15 min 时段各单元DES 的功率基线值及PFR 备用功率。进一步，各单元DES 依据当前时段的备用功率自动线性响应频率偏差，并通过叠加功率基线值以确定15 min 内秒级实时控制功率。

所提策略的在线算法流程详见附录B 图B1，各单元DES 实时控制的逻辑结构见附录B 图B2。

3 长期效益函数的离线计算

对于所提日内运行策略，其性能优劣的关键在于长期效益函数的离线计算效果。在3.1 节选取了决策后状态的可分分段线性函数（piecewise linear function，PLF）作为长期效益函数的近似形式，将Bellman 方程近似转化，进而在3.2 节采用TD（1）差分学习算法对近似效益函数离线训练。

3.1 长期效益函数的近似形式

通过向前递归Bellman 方程的ADP 公式，使得标准动态规划逆序计算全部条件期望的原始问题转化为正向训练PLF 分段斜率问题，从根本上降低了遍历求取期望效益面临的计算障碍。

3.2 近似值函数的离线训练

鉴于标准近似值迭代算法收敛缓慢，本文采用TD（1）算法对近似值函数开展离线训练。TD（1）算法是结合正向模拟及逆向更新的双向算法，其采用折扣因子λ=1 的时间差分学习过程加速PLF 斜率更新。首先，基于随机抽取的样本路径正向模拟序贯决策过程，沿样本路径向前递归求解式（28）得到各时段最优决策，从而计算各时段的边际贡献及边际流。然后，运用正向模拟所得边际贡献及边际流，在逆向更新时计算各时段的斜率抽样观察值，据此采用随机梯度下降法对PLF 斜率进行更新。TD（1）算法的具体步骤及流程详见附录C。

需要指出的是，随机对偶动态规划（stochastic dual dynamic programming,SDDP）算法与TD（1）算法类似，都属于缓解动态规划“维数灾”的可行方法，通过构造近似值函数并采用前后向迭代收敛至最优解。文献［26］对2 种方法从原理结构及运算性能方面进行了详细对比，结果发现随着资源维数的增长，SDDP 算法迭代收敛过程逐渐放缓，而TD（1）算法仍具有良好的迭代收敛效果。考虑到上述方法的运算性能差异，本文采用TD（1）算法对近似值函数迭代训练。

4 策略性能评估

为了对所提策略的性能量化评估，分别从离线训练效果和日内运行性能两方面进行分析。策略性能评估的具体流程及指标如附录D 图D1 所示。

1）离线训练效果评估

根据日前电价、负荷的预测数据及其误差分布、历史频率信息，生成R组训练场景以及Q组测试场景。基于上述R组训练场景开展离线迭代训练，运用第n次迭代训练更新的PLF 计算Q组测试场景的平均运行效益Fˉn，以此可视化迭代训练过程。进一步，定义了评估离线训练效果的收敛率指标ε，经过n次迭代训练后的收敛率可表示为:

式中:Fq，n为运用第n次迭代所得PLF 计算的测试场景q的运行效益；Fq，*为场景q的理论最优运行效益，其通过混合整数线性规划求得。

2）日内运行性能评估

对于日内运行性能的评估，分别需要从优化运算效果以及PFR 响应性能两方面进行分析。

通过模拟日内运行过程，依据其经济指标（日运行经济效益F、经济效益偏差率ζ）及运算指标（决策变量数Ns、求解时间Ts）量化评估优化运算效果。其中，经济效益偏差率是指日运行效益实际值F与理论最优值F*之间的偏差，即

关于PFR 响应性能的评估，首先需要验证各时段各调频单元备用功率Pf，sett之和是否满足中标容量PPFR，进一步辨识各调频单元的PFR 动态响应能力。此外，对计及等效需求系数的经济效益F及容量利用率Ue进行量化分析，其中容量利用率是指SOC 实际运行范围占可用空间的百分比。

5 算例分析

5.1 仿真参数设置

为验证所提策略的实际性能，以整合协调6 个单元DES 的聚合商为例开展仿真分析。考虑到不同储能的技术性能及商业化程度，各单元DES 均采用锂电池。所辖各单元DES 的额定功率、可用容量、充放电效率以及运行维护成本等参数见附录D表D1。日前PFR 市场出清后，实际中标容量为2.0 MW，出清价格cf=16.53 美元/(MW·h)［19］。

5.2 离线训练效果分析

基于日前电价、负荷的预测数据及其高斯分布误差，运用Monte-Carlo 模拟生成2 000 个训练场景及10 个测试场景，并从历史频率数据中以日为周期筛选相应规模的频率训练与测试场景。离线训练的最大迭代次数为2 500，各分段初始斜率均设置为零。由于harmonic 步长规则中的参数a以及随机信息的聚合水平h均会对训练过程的收敛性产生影响，本文采用控制变量法进行迭代训练，不同参数取值下的迭代过程及收敛结果如附录E 图E1 所示。由图E1 可知，在2 500 次迭代范围内，步长参数a与聚合水平h对迭代训练的收敛性影响显著。当取a= 1 500 且h=1 时，离线训练能够实现较好的收敛效果，相较于平均最优效益的收敛率高达98.37%。经过2 500 次离线迭代的运算耗时为3 305.6 s，单次迭代的平均计算开销为1.322 s。事实上，上述迭代过程仍存在1.63%的收敛偏差，其原因主要在于:随机信息的分层聚合策略难以做到精准的“状态-决策”映射，且差分学习算法的逆序更新采用随机梯度下降思想，对梯度估计的固有方差会阻碍进一步收敛。

5.3 不同策略的日内运算效果对比

为了验证所提LVFA 策略的日内运算效果，将之与DLA、SLA 策略的运算结果进行比较。不同策略的经济指标及运算指标结果如图4 所示。其中，变量数及求解时间是指日运行时域内每个滚动优化周期的平均数据。

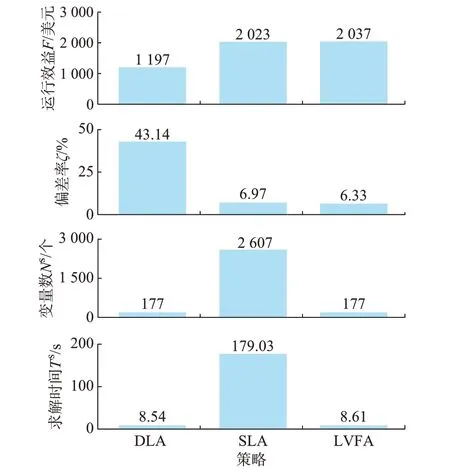
图4 不同策略的运算结果Fig.4 Calculation results of different strategies

由图4 中经济指标可知，LVFA 及SLA 策略均具有良好的运行效益，与理论最优效益2 282.07 美元的偏差率分别为6.33%和6.97%。DLA 策略的经济效益仅为1 197.65 美元，其偏差率高达43.14%。从优化模型角度分析，DLA 策略仅求解滚动时域4 h 内的优化模型以获取实时决策，其局部优化时域难以统筹全局运行，故对经济效益的影响最大；SLA 策略在线求解两阶段随机优化模型，而LVFA 策略采用值函数近似评估当前决策对长期时域的影响，2 种策略均从全局时域范围优化决策，相较于DLA 策略能够明显提升运行效益。

由运算指标可知，LVFA 策略在线滚动优化的单时段运算开销为8.61 s，与DLA 策略处于相同的计算维度，而SLA 策略求解时间高达179.03 s。从求解规模及决策变量数进行分析，DLA 求解短期时域内的确定性优化模型，平均变量数仅为177 个；LVFA 策略利用离线训练的PLF 表征当前决策对长期阶段的影响，显著降低了全局模型规模，故与DLA 策略具有相同的变量数。SLA 策略采用大量的样本路径构建长期时域的优化模型，通过场景缩减得到6 个典型场景，对应模型的变量数高达2 607 个，模型求解规模大幅增加，致使在线运算开销激增。

综合上述指标可知，LVFA 策略通过离线训练、在线应用模式克服了DLA 和SLA 策略各自运算性能的不足，可以在较短的时间内获得近似最优决策，有效兼顾了在线优化效果与求解时间。

5.4 所提策略的PFR 响应性能分析

1）备用容量及响应能力分析

各时段PFR 备用功率分布情况见附录E 图E2。由图可知，各时段全部调频单元的备用功率之和始终维持在2.0 MW，严格满足中标容量需求。为了直观反映具体单元提供PFR 的响应过程，图5 给出了单元5 的DES 日内运行功率及SOC 动态响应曲线。可以看出，各时段的功率基线与PFR 备用功率之和Pei，t±Pfi，t在额定功率上下限范围内，且当频率越过死区后，DES 能够在功率基线上叠加线性响应频率偏差的PFR 出力。根据SOC 动态曲线可知，即使在预测的最劣调频需求功率下，DES 响应过程中仍能够严格满足SOC 上下限约束，为PFR 服务提供可靠的电量裕度。综上可知，所提策略能够从功率及电量两方面保障日内运行过程中的PFR 响应能力。

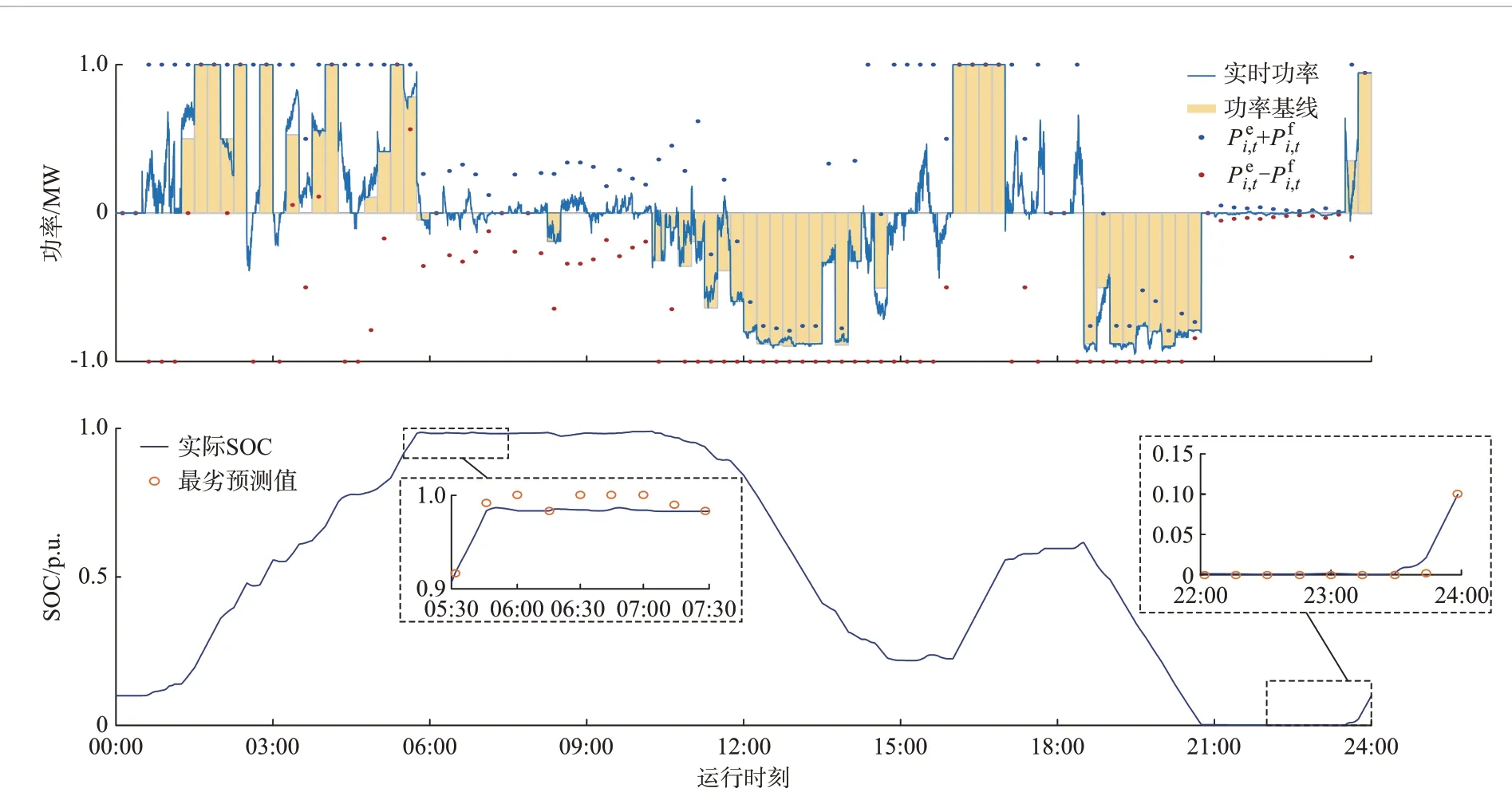
图5 单元5 的DES 功率及SOC 动态响应过程Fig.5 Dynamic response process of DES power and SOC for unit 5

2）等效需求系数影响分析

为了对等效需求系数的影响开展分析，将采用最大调频功率设置SOC 约束的情况作为基准对照组，而引入等效需求系数的情况作为改进组，分别量化其经济效益F和容量利用率Ue，结果如表1 所示。相对于基准对照组，改进组的经济效益提升1.63%。此外，DES 容量利用率由96.15%提升至97.92%，其原因在于:引入等效需求系数设置SOC 约束，能够在保障电量调节能力的同时降低SOC 空间浪费，拓展了DES 参与动态响应过程的可控空间范围，从而提升了DES 的经济效益与技术效用。