基于阶梯型需求响应机制的供需主从博弈电源规划模型

2022-10-31刘文霞王月汉

电力系统自动化 2022年20期

刘文霞，姚齐，王月汉，陈璐，鲁宇，2

（1. 华北电力大学电气与电子工程学院，北京市 102206；2. 国网吉林省电力有限公司经济技术研究院，吉林省长春市 130022）

0 引言

目前，中国电力系统正朝着低碳化、清洁化和可持续化转型。系统的电源结构、用电模式与市场机制都将发生深刻的变化，使系统的规划决策和运行控制面临着严峻挑战。电源规划是系统变革的源头，涉及源荷特性、市场机制和运行策略等众多因素，如何考虑和协调利用这些要素，深入研究电源规划的新方法，对提高系统经济性、安全性和低碳水平具有重要意义。

在低比例新能源并网阶段，电源规划通常根据电源跟踪负荷的运行规则，配置充裕的备用容量来保证电力平衡［1］；在运行模拟中，把新能源当作负的负荷处理或者将新能源机组等效成多状态发电机组［2］，根据规划期内的用电需求决策出各机组合理的利用小时数。在“双碳”的大背景下，碳交易等政策的出台［3］使得电源结构发生了深刻的变化。火电机组逐步让出发电主力位置，新能源机组所占比例大大提高，净负荷曲线将在新能源出力波动时段发生急剧变化［4］，系统短期动态特性将对电源规划的结果产生重要影响［5］。在运行模拟中，开始以小时为时间分辨率优化机组出力［6-7］。结果表明，在高比例新能源系统中，源荷双波动源使系统的灵活性需求剧增［8］，需要抽水蓄能、储能机组等灵活性资源对新能源出力的随机波动性进行补偿［9］。但是，现阶段抽水蓄能、储能等灵活性资源受技术成熟度或成本等限制难以大规模投建［10］，单纯依靠源侧资源难以满足系统经济性和安全性的双重要求，如何充分利用需求侧资源参与系统平衡得到关注。

需求侧管理（demand side management，DSM）工作的开展，为在电源规划中利用需求侧资源提供了有效途径。文献［11］将需求侧各类灵活性资源汇总为能效电厂参与系统的统一规划。文献［12］在电源规划模型中引入DSM 项目改善系统的负荷特性。随着电力市场化改革的深入，电力系统的利益主体逐渐多元化，需求响应（demand response，DR）开始引入电源规划中。文献［13-14］建立了基于电价弹性矩阵的用户多时段电价响应模型，通过制定分时电价引导用户进行“削峰填谷”，从而减少系统的装机容量和污染物的排放。文献［15］在考虑用户对电价DR 的基础上，实现了风-光-柴-储各类机组的优化配置。但在实际运行中，用户对电价信号的敏感度具有高度的不确定性，使得电力企业难以充分利用需求侧资源。相比而言，激励型DR 对电力企业来说更具备可操作性，对用户来说也更具有吸引力［16］。文献［17］将直接负荷控制引入电源规划中，通过削减峰荷实现系统规划总成本最小的目标。文献［18］按照中国江苏省现有的DR 补贴标准，调用需求侧资源配合电网电源侧满足系统的供需平衡要求。但上述研究中，DR 的补贴金额均按照固定标准，缺乏相应依据，且不利于调动用户的积极性。

为此，本文针对电力系统转型过程中的电源规划问题，通过分析碳交易、绿色证书机制、源荷特性和DR 等要素，建立了基于阶梯型DR 激励机制的供需主从博弈电源规划模型，并提出了求解方法。最后，以大规模风电并网为研究场景验证了模型的有效性和合理性，并分析了碳交易价格对规划结果的影响。

1 博弈关系分析及阶梯型DR 机制

1.1 碳交易与绿色证书交易机制

为鼓励新能源发电技术的发展，电力行业提出了多种激励措施。其中，碳交易与绿色证书交易机制的引入将系统运行过程中的碳排放量与新能源消纳量量化为经济价值，通过价格信号引导清洁能源的优化配置［19］。关于碳交易机制与绿色证书交易机制的具体过程分别见文献［3］和文献［19］。

1.2 基于DR 的供需两侧博弈关系论证

通过实施DR 引导需求侧资源参与系统的规划运行，已成为电力企业促进新能源消纳、优化电源结构的重要手段。但是，具有响应能力的用户数量众多且较为分散，且单个用户因多方限制响应约束较多，电力企业难以进行统一协调控制。因此，本文将各类用户整合聚集为负荷聚合商这一主体参与DR。负荷聚合商内的柔性负荷按照参与DR 的方式分为可削减、可转移两类。其中，可削减负荷包括空调用电负荷、热水器用电负荷等；可转移负荷包括电动汽车充电负荷、储电装置、储热罐等［20］。

目前，DR 的补贴资金均为由政府提供或者来源于专项资金，执行主体是电网公司［21］。而通过实施DR 改善负荷特性后，对电源和电网的设备规模、新能源消纳都产生了有益的作用。为此，考虑到DR、电源和电网的相关性，本文在电源规划阶段，将发电侧与电网侧统一作为供电侧主体，按照DR 后最大负荷计算电网投入，将各类电源和储能投入的规模和种类，以及引导需求侧的激励机制作为供电侧策略，与负荷聚合商进行交互，以实现源荷互动下的协同规划。图1 所示为系统运行示意图。

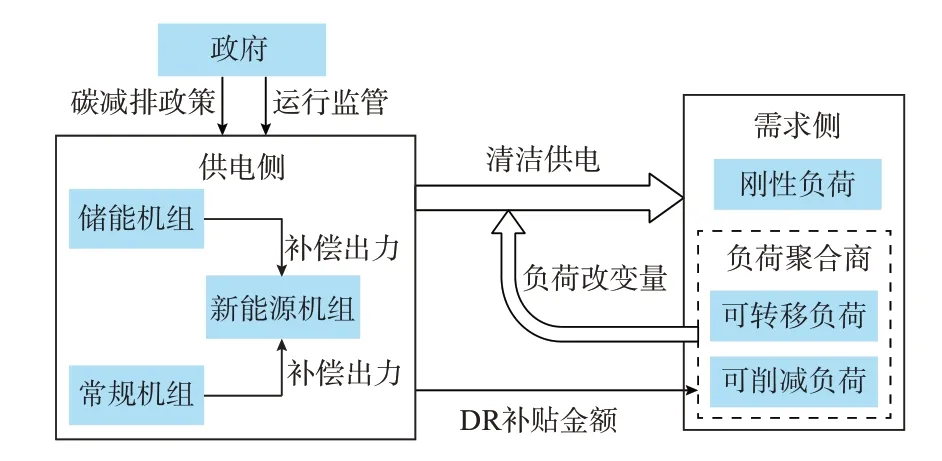
图1 源荷互动模式下的系统运行关系示意图Fig.1 Schematic diagram of system operation relationship in source-load interaction mode

在实施DR 的过程中，供电侧的目标是以尽可能低的成本引导负荷聚合商进行“削峰填谷”。而负荷聚合商的目标是根据供电侧给出的价格信号，决策得出使自身用电收益最大化的DR 响应量。两者之间的策略行为相互影响，存在博弈关系。而负荷聚合商的响应量是基于供电侧DR 的补贴金额决定的，响应量又会影响供电侧制定DR 的补贴金额以及电源的规划方案，此过程符合主从递阶结构的动态博弈情况。因此，本文将供电侧作为领导者，负荷聚合商作为跟随者，建立供需两侧主从博弈模型。

博弈模型中的参与者、策略、收益和均衡均为必备要素。上述博弈关系中，博弈要素如下:

1）参与者。供电侧和负荷聚合商作为参与者构成主从博弈，下文用S、L 表示两个参与者。

2）策略。领导者供电侧的策略为发电机组j的规划容量Sj和DR 项目在t时段的补贴金额Ct，dr；跟随者负荷聚合商的策略为参与DR 的响应量xt。

3）效用函数:供电侧以综合成本CS最小为目标，效用函数为CS(·)；负荷聚合商以用电效益FL最大为目标，效用函数为FL(·)。具体模型见下文。

1.3 阶梯型DR 激励机制

常规激励型DR 在某一时段的单位补贴金额固定，用户缺少选择。本文提出阶梯型DR 激励机制，根据参与DR 的时段和响应程度的差异给予不同的单位补贴金额，鼓励用户更大限度地参与DR。

为了引导负荷聚合商进行“削峰填谷”，分别在峰、谷时段设置多个激励区间，并独立优化峰、谷补贴金额，使负荷聚合商内的不同用户能根据自身用电特性灵活地选择响应方案。如附录A 图A1、图A2 所示，在负荷高峰时段，当用户的用电减少量达到削峰DR 的补贴条件后开始享受补贴，且补贴金额随着用电减少量的增多逐步提高。可表示如下:

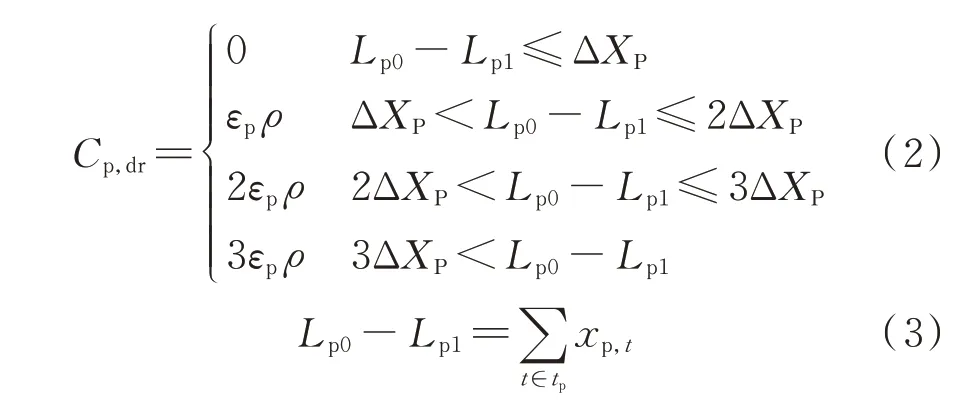
式中:Cp，dr为削峰电量单位补贴金额；Lp0-Lp1为负荷高峰时段用户的削峰响应电量；ρ为基准电价；εp为削峰激励系数；ΔXP为用户削峰响应量的参考值，因不同类型用户用电规模差别较大，为鼓励各类用户参与DR 并体现公平的原则，以各用户自身历史用电数据的百分比作为参考值；xp，t为t时段的削峰响应量；tp为负荷高峰时段集合。

在负荷低谷时段，当用户的用电增长量达到低谷DR 的补贴条件后开始享受补贴，且补贴金额随着用电增长量的增加逐步提高。可表示如下:

式中:Cv，dr为填谷电量单位补贴金额；Lv0-Lv1为负荷低谷时段用户的填谷响应电量；εv为填谷激励系数；ΔXV为用户填谷电量的参考值；xv，t为t时段的填谷响应量；tv为负荷低谷时段集合。

2 供电侧规划模型

为清晰阐述本文方法，以大规模风电并网为研究场景，考虑火电机组、风电机组、储能机组以及阶梯型DR 激励机制，建立以总成本最小为目标的双层电源规划模型。

2.1 上层规划

2.1.1 上层规划目标函数

上层规划的目标是在满足负荷需求及相关约束的前提下，使供电侧总成本最小。可表示为:

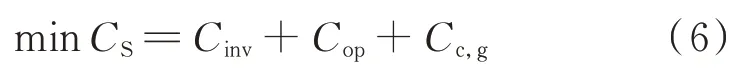
式中:Cinv为设备投资年等值成本；Cop为运行成本；Cc，g为碳交易与绿色证书机制成本。

1）投资成本

系统的投资成本主要包括电源机组的投建成本Cinv，g及输配电建设成本Cinv，n［21］，即

式中:ΩEP为待建机组集合；Cfj为机组j的静态投资成本；dj表示机组j的投建状态，为0-1 变量，1 表示投建、0 表示未投建；cn为输配电单位容量成本；ΔPL，max为最大负荷增长量；γj为机组j的年等值系数，可表示为

式中:τ为贴现率；Tj为机组j的运行年限。

2）运行成本

现有模型大多采用对几个典型场景运行模拟的方法［6］，难免会忽视某些小概率恶劣场景对规划结果的影响。为此，本文在计算运行成本Cop时包括了典型场景和小概率恶劣场景的运行成本:

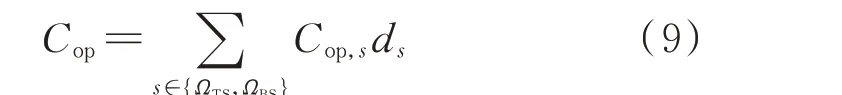
式中:ΩTS和ΩBS分别为典型场景和小概率恶劣场景集合；Cop，s为第s个场景的运行成本，由下层优化运行得到；ds为第s个场景的天数。

3）碳交易与绿色证书机制成本

式中:D为系统分到的碳排放配额，本文基于《2019年中国区域电网基准线排放因子》［22］，对系统的碳排放额度D进行分配（见式（12））；λco2为碳交易价格；V为实际碳排放量（见式（13））；Es为第s个场景系统内各机组总的发电量；φ为单位电量排放分配系数；Ωhot为火电机组集合；πco2为火电机组CO2排放系数；Eh，j，s为第s个场景火电机组j的发电量。

式中:本文取1 kW·h 为单位证书面值；N为系统要求的绿色证书指标；λtgc为绿色证书单位电量的交易价格；Mh为实际证书持有量（见式（15））；Ωwi为风电机组集合；Eg，j，s为第s个场景风电机组j的发电量。

2.1.2 上层规划约束条件

1）电力约束

系统的可利用功率应不小于其最大负荷需求:

式中:ΩCP为已有机组集合；PL，max为实施DR 后规划目标年最大负荷；RD为容量备用系数；Pj为机组j的单机容量或预想出力。对于火电厂而言，Pj取值为额定容量；对于风电机组而言，Pj取值为置信容量；对于储能机组而言，考虑其运行策略和存储电量的影响，Pj取值为其额定功率的50%［23］。

2）电量约束

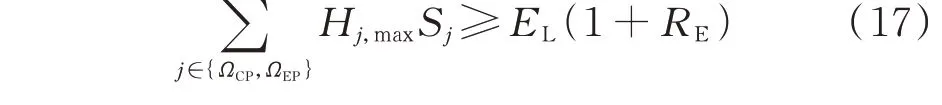
式中:Hj，max为机组j的年最大利用小时数；EL为规划目标年的用电量；RE为备用率。

3）最大最小利用小时约束

式中:Hj，min为机组j的年最小利用小时数；Ej为机组j的年发电量。

2.2 下层规划

2.2.1 下层规划目标函数

以运行成本最低为目标优化各设备出力以及DR 补贴金额。具体数学模型为:

式中:Cgen为机组发电成本；CS，dr为供电侧DR 项目实施成本；Closs为供电能力不足成本。具体如下式所示。

1）机组发电成本

式中:cj为机组j的单位发电成本；Pj，t为机组j在t时段的发电功率。

2）DR 实施成本

供电侧实施DR 的成本包括对负荷聚合商支付的补贴金额和因负荷需求改变后产生的收入差。可表示为:

2.2.2 下层规划约束条件

1）功率平衡约束

系统所有机组的发电功率等于此时的负荷需求，即

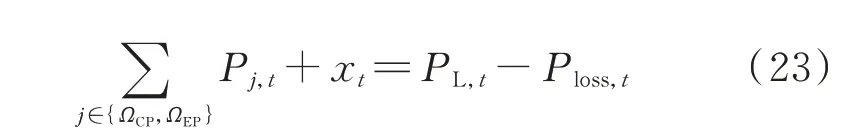
式中:PL，t为t时段的系统负荷需求。

式中:Uh，j，t表示火电机组j在t时段的运行状态；Ph，j，t为火电机组j在t时段的发电功率；Ph，j，up和Ph，j，down分别为火电机组j的向上爬坡速度限制和向下爬坡速度限制。

4）最小启停时间约束

5）储能运行状态约束

储能系统除充放电功率限制以外，还具有储能容量限制。为了满足调度需求，并保证储能能够连续稳定运行，设置储能系统在调度开始时的储能容量和调度窗口结束时的储能容量相同［24］，即

3 负荷聚合商规划模型

3.1 规划模型目标函数

负荷聚合商根据供电侧给出的DR 激励方案，调整负荷响应量，实现用电效益的最大化，即

式中:Fdr为负荷聚合商参与DR 项目获得的收益；CL，dr为负荷聚合商的响应成本。收益为负荷聚合商从供电侧获得的经济补偿，可表示为:

式中:Ωdr为负荷聚合商内柔性负荷的集合，包括可平移负荷和可削减负荷；xi，t为第i类柔性负荷在t时段的响应电量。

响应成本包括负荷聚合商参与DR 带来的用电量成本和改变用电行为带来的不舒适成本，通常是非递减且凸的，有二次型［25］、对数型［26］等几种形式。本文采用二次型来表示:

式中:ui和vi为第i类柔性负荷的舒适度系数，其大小根据用户的用电习惯决定。

3.2 规划模型约束条件

1）负荷改变量约束。负荷聚合商在某一时段的响应量不能超过其响应能力，即

式中:xi，max，t和xi，min，t分别为负荷聚合商内第i类柔性负荷在t时段响应量的上、下限。

2）用电需求约束。负荷聚合商参与DR 应以满足其内部用户的基本用电需求为前提，即

式中:ΔEL，i，max为第i类柔性负荷在调度周期内用电改变量的最大值。

4 主从博弈模型求解

4.1 分段问题的转化

阶梯型DR 激励方案中，不同的激励区间对应不同的单位补贴金额，因此，负荷聚合商参与DR 的收益函数为一个分段函数。通过大M 法和分段线性化将其转化为混合整数二次规划（mixed-integer quadratic programming，MIQP）问题进行求解。以削峰激励方案中第k个激励区间为例，步骤如下。

加入等式约束:

式中:K为阶梯型激励方案的激励区间数；δk为第k个激励区间对应的0-1 变量。

引入无穷大的正整数M，并加入不等式约束:

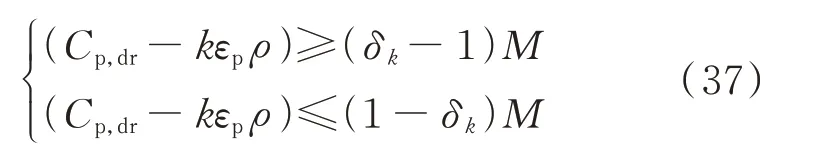
加入不等式约束:

式中:Llow，k和Lhigh，k分别为第k个激励区间对应的响应下限和响应上限。

4.2 双线性项问题的求解

在求解供电侧规划模型时，将其转化为混合整数线性规划（mixed-integer linear programming，MILP）问题进行求解。对于其中的双线性项，使用线性化的方法将其转化为线性约束。步骤如下。

只有当机组处于投运状态且处于开机状态时，才可以进行发电。以式（24）机组出力约束为例，可表示为:

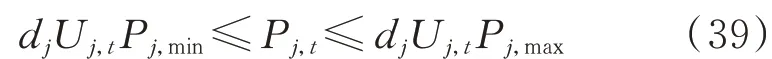
此时，对于待投建机组约束条件中存在双线性项。为此，加入以下线性约束:

式中:αj，t为引入的中间变量，表示待建机组j在t时段的运行状态。

从而将式（39）转化为:

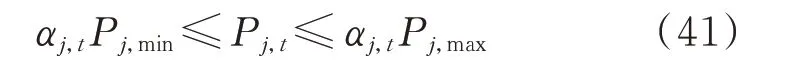
4.3 博弈求解过程

基于DR 的电源规划问题以供需双方的电量交互为参考。供电侧的电源规划方案受负荷聚合商响应量影响，而电源规划方案会影响供电侧对供需平衡的调控能力，进而影响供电侧在价格信号决策上的主动权。因此，应该在DR 完成后再进行电源规划。

博弈可分为3 个阶段进行求解:首先，通过差分进化算法生成供电侧DR 激励方案传递给负荷聚合商，即第1 阶段决策；然后，调用Gurobi 求解器求解负荷聚合商的MIQP 问题，决策出使其用电效益最大的响应策略，即第2 阶段决策；此时，供电侧得到新的负荷曲线，在此基础上进行电源规划，属于MILP 问题，调用Gurobi 求解器进行求解并将结果返回到上层的适应度函数中，即第3 阶段决策，此时供电侧的总成本，即第1 阶段差分进化算法中的适应度函数亦可求得。由于第2、第3 阶段分别采用MIQP 和MILP，当其求得各自的最优时即为子博弈均衡。而当第1 阶段差分进化算法相邻两代寻得的最优DR 方案相同时，即可认为供电侧和负荷聚合商在各阶段均达到最优，多阶段主从博弈达到子博弈完美均衡［25］。主从博弈收敛性及最优均衡解存在性的证明和具体算法流程见附录A 和图A3。

5 算例分析

5.1 基本参数

以中国北方某地区目标年电源规划为例进行分析。该地区当前年用电量为609 GW·h，最高负荷为87.90 MW，预计到目标年负荷用电量将增长到1 541 GW·h，最高负荷达223.53 MW。已有和待选电源装机结构及设备参数如附录B 表B1 至表B3 所示。绿色证书交易价格设为0.3 元/（kW·h），设定仿真系统可再生能源发电量要求占系统总能源需求的30%。碳交易价格为300 元/t，单位电量排放分配系数为0.7 kg/（kW·h）。取用户峰、谷时段历史用电量的5%作为阶梯型DR 分档的参考值。

典型场景选取夏、冬季2 个典型日，其负荷曲线如附录B 图B1 所示，基准电价为0.8 元/（kW·h）。可削减负荷的舒适系数分别取0.05 和0.80；可转移负荷的不舒适系数分别取0.03 和0.85。小概率恶劣场景选择负荷与风电出力差值最大的场景，如附录B图B2 所示，单位缺电惩罚成本为16.0 元/（kW·h）［27］。根据负荷特性，将00:00—04:00 划分为低谷时段，05:00—10:00、13:00—15:00 和19:00—23:00 划分为平时段，11:00—12:00 和16:00—18:00 划分为峰时段。

5.2 结果分析

为分析实施DR 对电源规划结果的影响，以及本文所提阶梯型DR 激励机制的作用，设置3 个场景进行对比分析:

场景1:考虑碳减排政策但不实施DR；

场景2:考虑碳减排政策并实施常规型DR；

场景3:考虑碳减排政策并实施阶梯型DR。

各场景下得到的规划结果如表1 所示。

表1 各场景规划结果及成本对比Table 1 Planning results and cost comparison of each scenario

从表1 可以看出，考虑DR 机制后电源规划结果发生了变化，主要体现在储能机组规划容量的减少以及成本的降低。其中，场景3 实施了阶梯型DR 激励机制，相较于场景2，储能机组的规划容量减少了5.00 MW，投资和运行成本分别降低了460.00 万元和73.82 万元，碳交易与绿色证书收益提高了89.00 万元。为更加直观地体现实施DR 的影响和阶梯型DR 激励机制的特点，以冬季典型日为例进行深入分析。表2 给出了场景2 和场景3 中，负荷聚合商内的两类柔性负荷参与DR 的优化结果。图2给出了场景3 冬季典型日的仿真结果。

图2 冬季典型日仿真结果Fig.2 Simulation results of a typical day in winter

表2 场景2、3 中两类负荷参与DR 的优化结果Table 2 Optimal results of two types of loads participating in DR in scenarios 2 and 3

可以看出，通过给予负荷聚合商一定的经济补偿引导其参与DR，能够有效地实现削峰填谷和平抑负荷曲线。在场景3 中，负荷聚合商内的柔性负荷在峰、谷时段的响应程度越大，享受的单位补贴金额越高。相较于场景2，场景3 的削峰和填谷响应电量分别增加了12.43%和38.79%。

5.3 主从博弈过程分析

5.3.1 供电侧成本变化分析

图3 反映了供电侧的总成本随εp和εv的变化趋势。图中，A、B、C、D 分别对应补贴金额为0、总成本最小、总成本最大、补贴金额最大4 个方案。相应的规划结果如表3 所示。

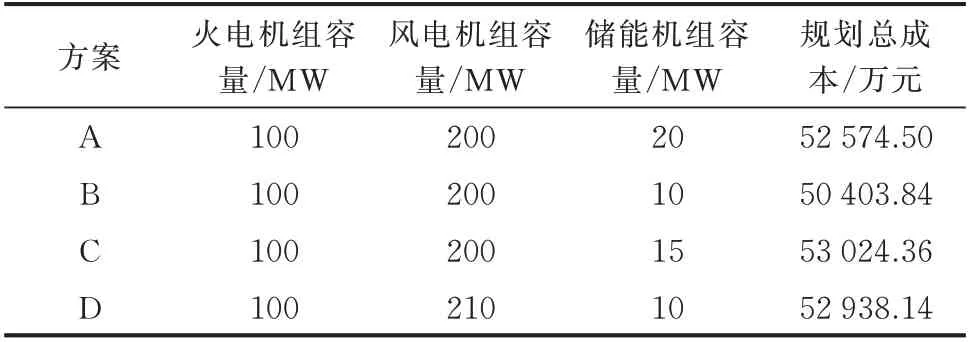
表3 不同方案规划结果Table 3 Planning results with different schemes

图3 供电侧总成本变化Fig.3 Variation of total cost on power supply side

当εp和εv为0 或较小时，负荷聚合商不参与DR，仅靠供电侧资源满足用电需求，此时成本较大为52 574.50 万元。而随着激励系数变大，负荷聚合商分担了供电侧的供电压力，供电侧总成本开始变小，当εp和εv分别为0.10 和0.14 时系统总成本达到最小。但随着激励系数进一步变大，系统的总成本升高，当εp和εv分别为0.50 和0.24 时系统总成本达到最大。当εp和εv均达到0.50 后，相较于方案C，系统多投建了10 MW 的风电机组，并降低了5 MW 储能机组的投建，总成本降低了86.22 万元。这是由于进一步增大εv后，激励负荷聚合商更大限度地参与填谷DR，促进了风电消纳，并在一定程度上提升了系统的经济性。

5.3.2 负荷聚合商响应量变化分析

本节以冬季典型日可转移负荷的削峰量为例，分析εp和εv对DR 结果的影响。图4 所示为负荷聚合商内可转移负荷削峰响应量随εp和εv的变化曲面。

图4 可转移负荷削峰响应变化Fig.4 Variation of peak shaving response of transferable load

可转移负荷的削峰响应量同时受εp和εv的影响。当εp和εv较小时，不参与DR。随着εp和εv的增大，用户的削峰响应量逐渐增多，且大致可分为4 个阶段，分别对应阶梯型激励方案的4 个激励区间。当可转移负荷的响应能力达到上限后，供电侧无法通过增大εp和εv来激励其更大限度地参与削峰DR。

5.4 碳交易价格影响分析

火电机组作为发电侧占比最大的可调度机组受碳交易价格影响。设定碳交易价格为0～600 元/t，对本文所提电源规划模型进行求解，规划结果如图5 所示。

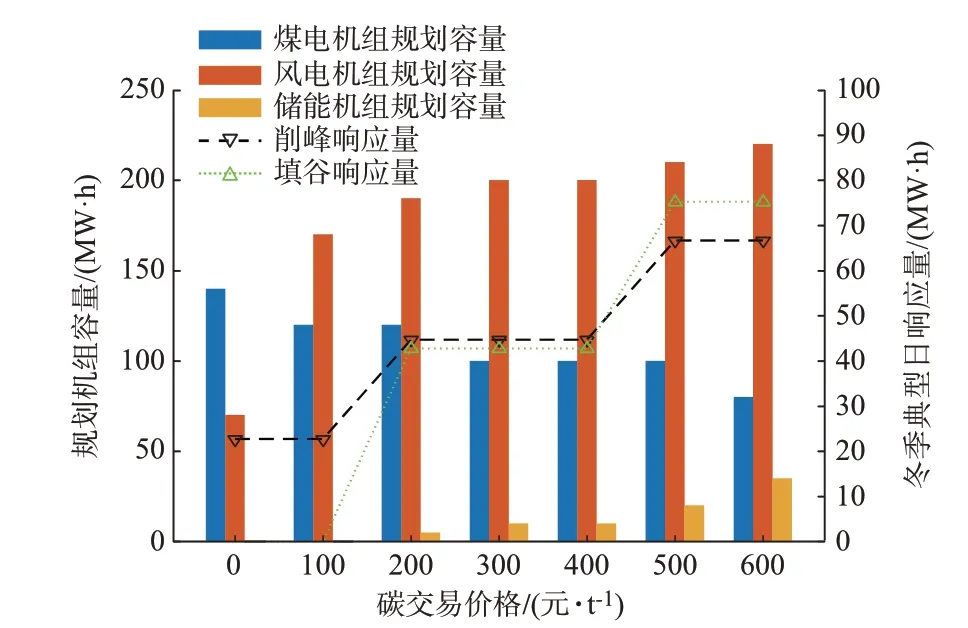
图5 碳交易价格对规划结果的影响Fig.5 Impact of carbon trading price on planning results

可以看出，当碳交易价格为0 元/t 时，火电机组的规划容量占比较高，且未规划储能机组。冬季典型日供电侧调用负荷聚合商的削峰和填谷量分别为22.70 MW·h 和0 MW·h。随着碳交易价格的升高，火电机组的规划容量逐步降低，风电、储能机组的规划容量以及引导负荷聚合商参与DR 的需求逐步升高。当碳交易价格上升到500 元/t 后，供电侧对于负荷聚合商的填谷需求超过了削峰需求。