方程与不等式中的数学思想

201108 上海星河湾双语学校 胡清湉

现实问题中的数量关系分为相等关系和不等关系两种

.

其中，相等关系衍生为“方程”，不等关系衍生为“不等式”，方程和不等式是初等数学中解决数量关系现实问题的有力工具之一，简洁高效

.

又因为两者蕴含着丰富的数学思想，因此它们成为数学学习过程中一个重要组成部分

.

受传统教育模式的影响，部分教师在教学过程中忽视知识与概念背后的数学思想，缺乏对于数学概念整体的思考

.

笔者以“一次方程和不等式”为例，深入剖析在教学中需要重点渗透的数学思想

.

一、 方程与不等式的核心思想

从数学学习的角度出发，概念既需要分类，亦需要结构化的思考，将各种知识点和方法融会贯通后抽象成一个概念体系，并能够使用该抽象的概念体系逐步进行推理和建立模型，以解决更多问题

.

小学到中学阶段，无论是国内还是国外的教材，都将“方程与不等式”列为课程标准中的一个举足轻重的篇章

.

以实际问题为背景，由基本等量关系而建立起来的代数方程有着非常高的实用价值，用方程求解实际问题能够以静制动、化逆为顺

.

另一个非常重要的原因是，从代数角度来看，方程与不等式为“式”；而从图形角度来看，方程与不等式则为“形”，它们更是数形结合的产物

.

方程与平面以及空间几何图形(如点、直线、曲线、平面、曲面等)都有对应关系；而不等式则是以对应方程为边界的一些区域

.

方程与不等式之间“对立与统一”的关系使得两者的联系更为紧密，它们也是抽象思维和形象思维高度结合的产物

.

二、 方程的初步认识

方程的学习在国内外教材中普遍始于小学高年级阶段，在此之前，学生基本使用算术方法解决问题

.

用算术方法解决问题的过程中，学生有时会使用逆向思维，而对于此类问题，使用方程求解能够起到“化逆为顺”的作用

.

如《九章算术》中有以下盈亏问题

.

今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？

(1)算术方法求解：在每个人出的金额不变的前提下，人数从8个变成7个时，原本总金额从还能盈余3元变成亏损4元，则人数为(3+4)÷(8-7)=7(个)，物价为8×7-3=53(元)

.

(2)使用方程求解：假设有

x

个人，根据物价不变性质列出等式8

x

-3=7

x

+4,

x

=7(个)

.

在该盈亏问题的方程求解过程中，通过假设变量，顺利地将一个实际问题转化为求解变量的问题，体现出从具体到抽象的思想

.

通过假设变量，能够将求解“已知”转化为“未知”，体现出化归思想

.

算术方法的根本是找出“变化关系”，与算术方法相比，方程的本质是找出等量关系，“以静制动”，通过分析等量关系，从而能够更为简洁地解决实际问题

.

一年级到四年级的学生基本使用算术方法解决问题，但随着解决问题难度的增加，算术问题往往不容易求解，这时方程就体现出它的优势了

.

例如，对于问题“把一张正方形的纸剪成若干个小正方形，如果剪成边长为2厘米的小正方形，剪出的小正方形个数比剪成边长为3厘米的小正方形多20个，两种剪法都正好用完纸，原来这张正方形纸的面积是多少平方厘米？”根据正方形的面积不变，列出等量关系，根据两种情况下原正方形面积的表示方法，可以得出相应的方程

.

按照顺向思维，找准等量关系就能够迅速求解，简言之，这就是“方程思想”

.

学生在小学阶段重点学习一元一次方程的求解方式，一元一次方程的解在数轴上实质即为一个点

.

作为方程的初步学习，一元一次方程的思想也为后续初高中方程和不等式的学习奠定了基础

.

三、 方程的“式与形”

方程的“式与形”示意图如图1所示

.

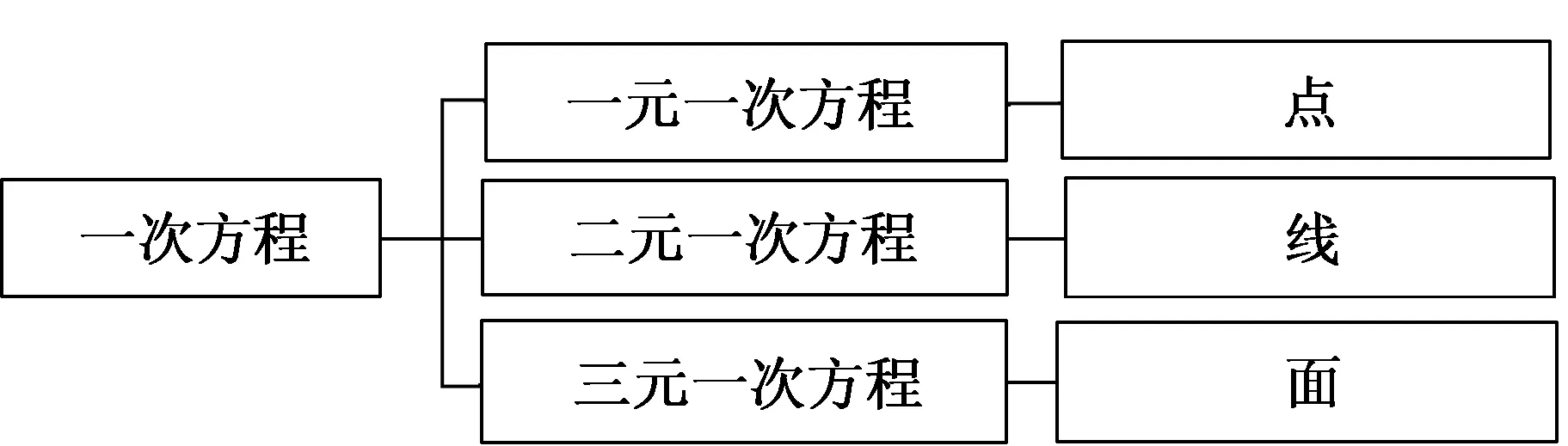
图1

一次方程(或称线性方程)是初中学习的重点，其主要包括一元一次方程、二元一次方程、三元一次方程

.

与之相对应的是一次方程组，主要包括二元一次方程组、三元一次方程组

.

前文已经提及一元一次方程的解在数轴上体现为一个点

.

再看二元一次方程，它的代数形式为

Ax

+

By

=

C

(

A

,

B

,

C

是实数)，其在直角坐标系中所有符合条件的点的集合{(

x

,

y

)|

Ax

+

By

=

C

}为一条直线，即一次函数

.

因而，在美国Common Core课程标准中，二元一次方程被称为“Linear Equation with two variables”(含有两个变量的一次方程)

.

作为函数而言，其性质也值得深入讨论，在此仅从方程组角度进行剖析

.

二元一次方程组在初中数学学习中占据很重要的部分

.

对于二元一次方程组的解集，从“数”的角度出发，可以通过联立方程组求得公共解；从“形”的角度出发，可以通过绘制直线图形求得公共解

.

将解集与公共点有机结合，这其中蕴含的就是数形结合思想，无形的式与有形的图结合在一起，把抽象的代数问题转化为形象化的问题，便于学生理解和分析

.

典型例题如下

.

例题

某手机话费运营商提供两种话费套餐，套餐1为基础月租费40元，此外每分钟收取0

.

2元电话费；套餐2为月租费60元，不限电话使用时间

.

请问每月打多少分钟电话时，两种套餐总价一样？

求解：

假设每月打电话

x

分钟，每月话费总价为

y

元，则可以列出二元一次方程组通过求解，可得方程组的解如果从图像上分析，可以清晰地看出这两个二元一次方程代表的两条直线的位置关系是相交，而交点(100,60)正是该方程组的解(如图2所示)

.

从代数角度看，通过联立方程组得到公共解；从图形角度看，两条直线的交点就是方程组的公共解

.

在该典型例题的讲解过程中，将代数方程组的求解问题与两直线位置关系结合进行教学，学生能够对于方程组的本质有更深入的理解，从而更好地理解数形结合思想

.

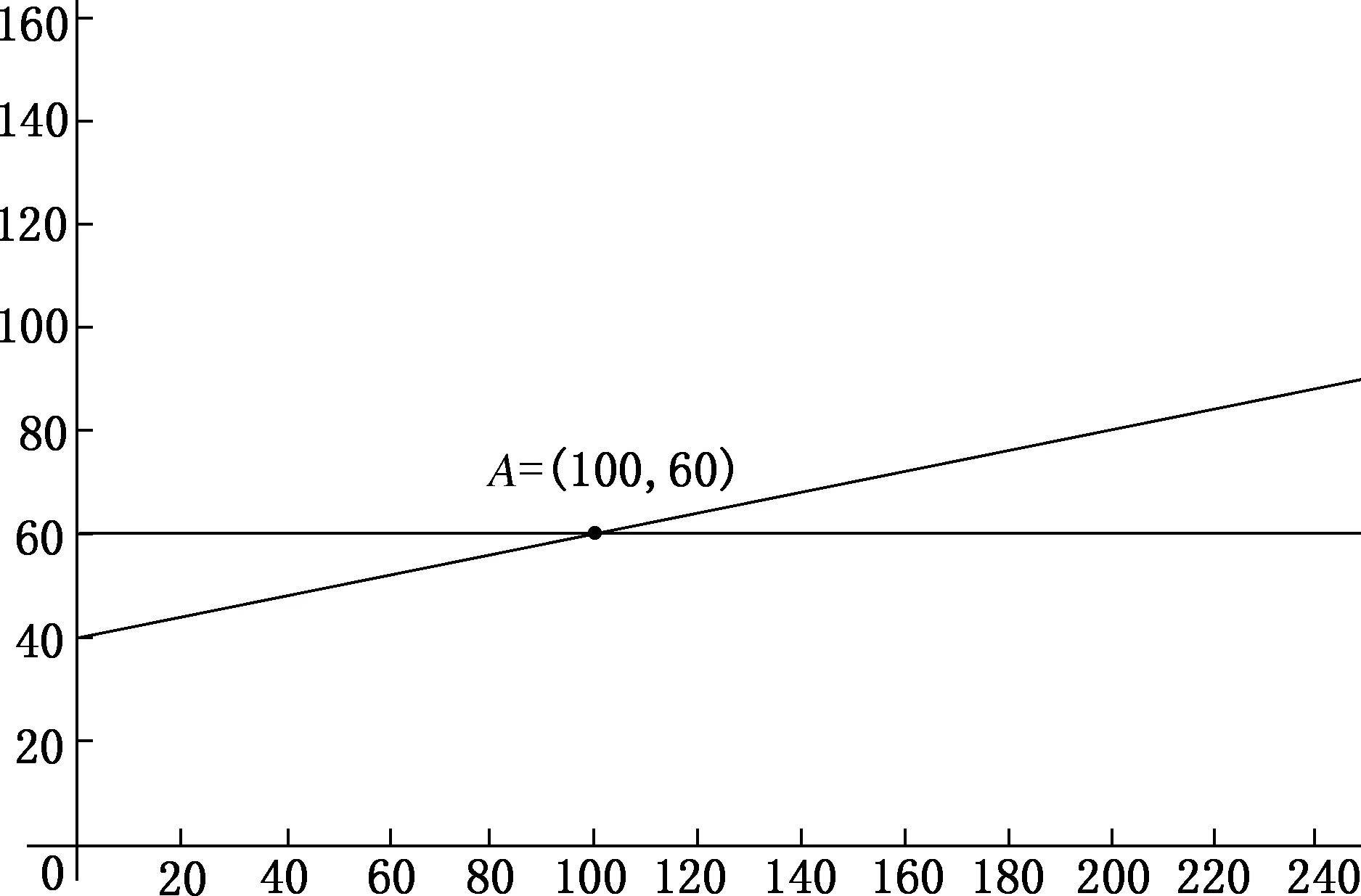
图2

美国Common Core课程标准将二元一次方程组中两个方程之间的兼容性和独立性分为三类，即平行(无交点)、相交(1个交点)、重合(无数个交点)，对应inconsistent system(不兼容系统),consistent and independent system(兼容且独立系统),consistent and dependent system(兼容且依赖系统).

在国内外课程体系中，两条直线的三种位置关系判断也有类似的阐述

.

美国教材在八年级讲解如何通过直线的斜率和

y

轴截距进行判断(如图3所示)；而沪教版教材中，这部分内容在高二年级讲解，采用的方法基本为使用系数行列式进行判断

.

对比这两种方法，其本质都是通过一定的代数式运算，得出有关图形之间的关系，并能够得出方程组解的个数的判断

.

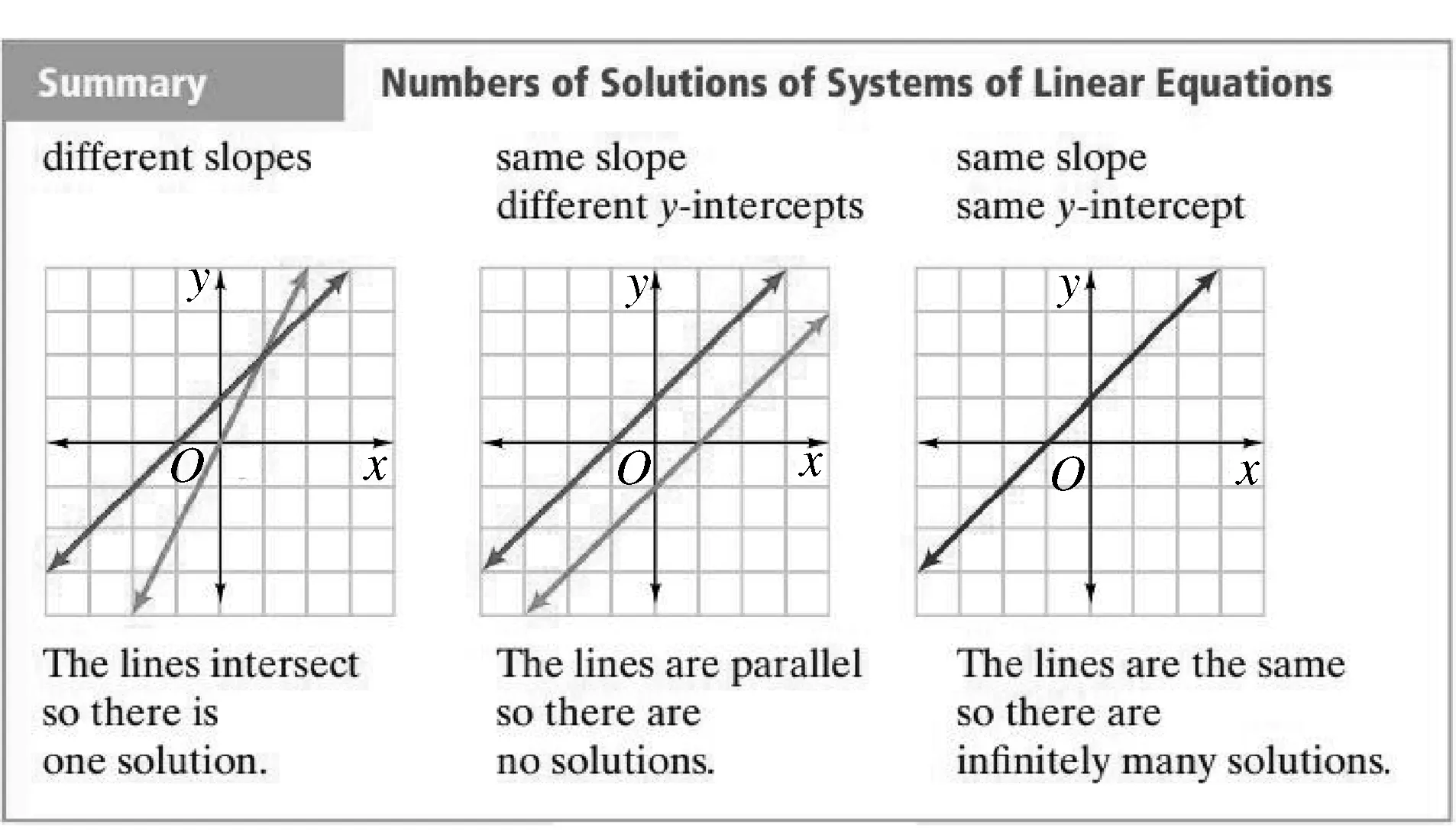
图3

在内容安排上，国内外一致将二元一次方程组的代数求解放在六年级、七年级左右，并强调通过“代入”和“加减”消元法求解方程组，这样求解方程组的思想即是“化归”的算法思想

.

学生在后续学习分式方程、根式方程以及高次方程时，都可以使用化归思想，体会不同类型的代数方程可以相互转化的辩证观点

.

以此类推可以得到的是，三元一次方程的代数形式为

Ax

+

By

+

Cz

=

D

(

A

,

B

,

C

,

D

是实数)在空间坐标系中所有符合条件的点的集合{(

x

,

y

,

z

)|

Ax

+

By

+

Cz

=

D

}是以为法向量的空间平面

.

一次方程从一元、二元到三元，在代数形式上层层递进，在几何图形上步步进阶

.

中学阶段的方程学习基本到三元一次方程为止，当延伸到高等应用数学分析等量关系时，线性方程具备独特的规律性，许多非线性方程都可以通过线性方程进行有效模拟，是数学建模的首选

.

四、 不等式的“式与形”

不等式的“式与形”示意图如图4所示

.

图4

一元一次不等式

Ax

>

B

或

Ax

≥

B

(

A

,

B

是实数)的解集体现为数轴上的某一段

.

例如，2

x

-6≤-8的解集用集合表示为{

x

|

x

≤-1}或者(-∞,-1],在数轴上体现为以-1为端点(包括-1)向左延伸的射线，这即是数轴表示法，数轴表达方式也是数形结合的开端

.

对于一元一次不等式组来说，结合集合关系建立起来的交集与并集的运算更丰富了不等式组的内涵

.

例如，以下一元一次不等式组(包含2个不等式)的解集表示如表1所示，假设其中常量

a

>

b

，并仅讨论>或<的情形(≥或≤的情况可以类比得到)

.

在美国Common Core课程标准中，一元一次不等式组解集的表示被设置在八年级上学期学习，前序知识为一元一次不等式以及集合的初步认识，这让八年级的学生初步体会了数形结合的思想.不过，因为涉及“逻辑判断”思想，基于集合概念的一元一次不等式组的解集的运算，对于八年级学生来说仍然是一个难点，所以，需要经过逐步消化后才能够在高中进一步拓展，这也符合了美国教材螺旋上升的基本框架.在国内的沪教版教材中，不等式组以交集为关联方式的形式被设置在六年级下学期学习，前序知识为二元一次方程组的学习，但这部分的内容仅以基本不等式为表达形式，并没有加入集合的概念，仅加强了以数形结合为主的不等式组在数轴上的解集表示.沪教版教材涉及的集合概念将在高一展开深入讲解，这也能够让学生在初中阶段更好地打下运算求解、推理论证和数学表达能力的基础.此外，沪教版初中教材的另一个特点是没有出现不等式组以并集为关联方式的形式，但是学生在解决实际问题过程中采用的“分类讨论”策略，其实就是并集逻辑思想的具体体现.

表1

一元一次不等式组的解集表示 (a>b)交集的式交集的形-∞,a ∩-∞,b =-∞,b a,+∞ ∩b,+∞ =a,+∞ -∞,a ∩b,+∞ =b,a a,+∞ ∩-∞,b =Ø并集的式并集的形-∞,a ∪-∞,b =-∞,a a,+∞ ∪b,+∞ =b,+∞ -∞,a ∪b,+∞ =-∞,+∞ a,+∞ ∪-∞,b =a,+∞ ∪-∞,b

二元一次不等式的代数形式为

Ax

+

By

>

C

或

Ax

+

By

≥

C

(

A

,

B

,

C

是实数)，其在直角坐标系中所有符合条件的点的集合，是以

Ax

+

By

=

C

为边界的半平面区域

.

如此，二元一次方程与二元一次不等式在平面内高度融合在一起，“相等”代表边界线，“不等”代表半平面区域

.

如以下例题

.

例题

请用不等式组表示出图5中的点线与实线的重合区域

.

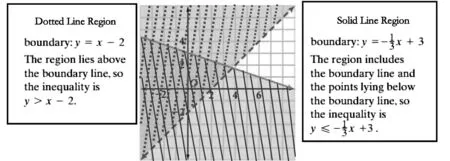
图5

分析：

图中点线区域的边界线方程为

y

=

x

-2，点线区域位于边界线的上方，所以描述点线区域的不等式即为

y

>

x

-2

.

图中实线区域的边界线方程为实线区域位于边界线的下方，所以描述实线区域的不等式即为从而可以确定不等式组为方程和不等式有机地结合在图像中，体现出“对立与统一的”思想

.

首先要看出“边界线”等同于“方程”，再者就是要把“半平面区域”看作“不等式”，“相交部分”即为“不等式组解集”，从而图像问题与代数问题能够进行相互表达

.

本质上，二元一次不等式组类型的问题能够很好地培养和发展学生的空间观念和数感，从而进行形象思维和抽象思维的交叉运用，使得多种思维互相促进，有助于培养学生灵活应用数学知识的能力

.

在线性规划问题中，二元一次不等式组或多元一次不等式组是“约束条件”，再加上“目标函数”，即为完整的线性规划问题

.

线性规划是运筹学中一个重要分支，主要研究线性约束条件下目标函数的极值问题

.

美国Common Core课程标准中，将通过线性规划建模实际问题中的找出约束条件以及求解目标函数极值问题，分为两步，分别设置在八年级、十年级学习

.

如八年级阶段有如下例题

.

例题

某动物园管理员准备为山羊区做一个围栏，围栏的长至少要80米，围栏周长不超过310米，问围栏可能的长、宽分别是多少？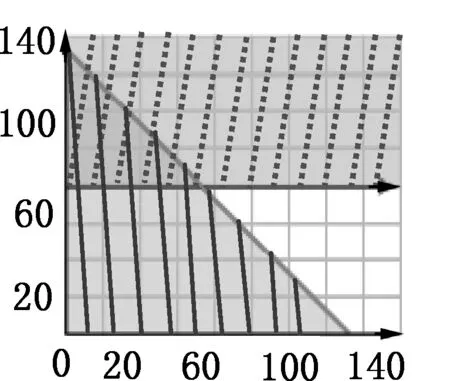

图6

求解：

假设围栏的宽是

x

米, 长是

y

米，因此围栏符合的不等式组为如图6，根据不等式组的图像表示形式，容易得到图解为点线和实线重合区域，而两条直线代表的方程，正是重合区域的边界线

.

在问题中“数”的表达形式，联系到“形”的表现形式，把似乎是纯代数的问题，在“形”的引导下，有了最好的解决方式，由抽象到具象，形中有数，就是“数形结合”的思想方法

.

沪教版教材统一设置在高二学习，这样能够让学生初步感受整体“建模思想”，尤其是对于略复杂的实际背景问题，如何准确描述出目标函数和约束条件，把实际问题转化为线性规划问题，也是用数学解决生活问题的很好的实践体验，而这类问题也是现代管理科学的重要理论基础

.

至此，笔者已对方程与不等式的概念体系进行了初步探究，并根据实际教学过程中需要体现出的教学重点展开分析，旨在培养学生对方程与不等式的结构化思考，重点体会其中蕴含的数形结合思想，认识相互之间的对立与统一，培养学生抽象思维、逻辑推理和建立模型等方面综合运用的素养和能力，感受数学文化之美，关注对于创新思维和创造能力的培养

.