基于ANSYS Workbench 的深孔内圆磨杆静动态特性分析
2022-10-30梅灵青
梅灵青
(200093 上海市 上海理工大学 机械工程学院)
0 引言
具有深孔薄壁结构的套筒和作动筒等是飞机起落架的关键零件,其内径和孔深之比可达1:10,且材料多为超高强度钢或钛合金整体锻造[1]。为提升飞机整体性能,这些零件均需要进行深孔精加工,以此保证零件加工质量要求。目前,对飞机起落架套筒类大长径比深孔零件精加工主要采用数控深孔内圆磨床,深孔内圆磨床的磨杆直接参与深孔磨削加工,它的静动态特性直接影响到磨床的加工精度[2],其刚度与振动性能的好坏直接影响到内圆磨床的工作性能,因此对磨杆系统进行研究分析是十分必要的。本文运用ANSYS Workbench 软件对某型号磨杆进行静、动态性能分析,为后续该类型磨杆的设计和优化奠定基础。
1 磨杆有限元模型的建立
1.1 磨杆系统结构的介绍
深孔磨杆结构如图1 所示,主要由主轴、偏心套筒、前端轴承、后端轴承和皮带轮等零件组成。主轴采用9Mn2V 材料,前端通过螺钉与砂轮相连,后端采用锥孔定位、螺钉固定的方式与皮带轮相连接,为系统提供传递扭矩的作用。偏心套筒材料为45 钢,采用偏心圆截面设计,使得磨杆在磨削力与重力载荷作用下具备高刚度特性。主轴前端支撑为前后两组角接触球轴承,型号为NSK7205C,背对背安装,每组2 个同向布置,采用定压预紧方式,其预紧力大小可通过调节预紧弹簧而改变。后端支撑采用2 个角接触球轴承,背对背安装,型号为NSK7206C,后端轴承采用定位预紧,能通过锁紧螺母调节预紧力大小。
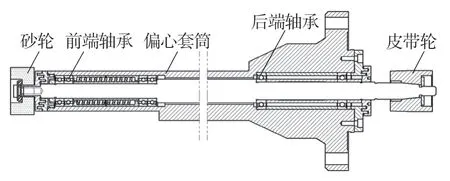
图1 内圆磨杆结构简图Fig.1 Structure diagram of internal grinding tool
1.2 磨杆系统有限元模型的建立
有限元模型直接影响仿真计算结果,也是进行磨杆优化设计的基础,建立准确合理的有限元模型对于深孔磨杆静动态性能的研究尤为重要。磨杆系统的组成零件多且某些零件结构复杂,建模过程中,在不改变零件模型特征的基础上,可将各零件上对分析结果影响较小的凹槽、退刀槽、倒角以及螺纹等细小特征适当简化,可节省计算机运算能力且不会对仿真结果产生较大影响。
将简化后的三维模型导入到ANSYS Workbench18.0,对几何模型进行网格划分,设置单元尺寸 (element size) 为5 mm,网格类型为四面体单元类型,生成节点与网格单元。整个磨杆系统体划分出726 689 单元,447 070 个节点。图2 为磨杆的有限元模型。

图2 网格划分Fig.2 Mesh division
设置各零件材料类型,各材料属性如表1所示。
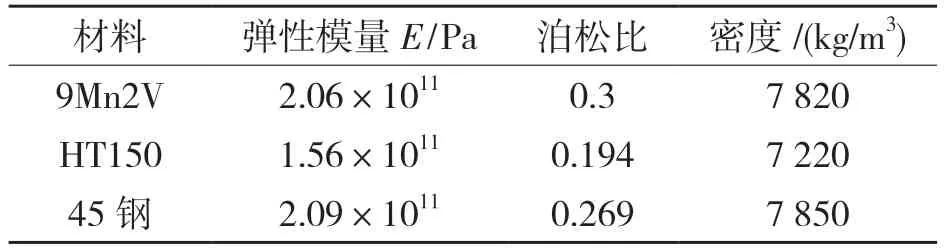
表1 零部件材料属性Tab.1 Material properties of components
1.3 载荷约束的分析
在内圆磨削时,砂轮与工件的磨削力可以分解为互相垂直的3 个分力,分别为砂轮切削面圆周切线方向的切向磨削力 Fc、砂轮切削面圆周法线方向的径向磨削力Fp、砂轮架轴向进给方向的轴向磨削力Fa。在实际磨削过程中,由于轴向磨削力很小,在分析时可忽略不计,只需考虑切向磨削力和径向磨削力[3]。根据实际加工情况,磨杆最大径向磨削力取200 N,切向磨削力取60 N,皮带轮压轴力取300 N。
2 磨杆静态特性分析
2.1 静态仿真特性分析
在Workbench 中的static structural 模块对磨杆进行静力学特性仿真分析,静态性能分析的目的是研究磨杆系统在磨削力与自身重力载荷作用下的应力与变形情况。
在砂轮外表面施加200 N 的径向磨削力与60 N 的切向磨削力;在皮带轮与平带接触的表面上施加300 N 的压轴力,方向竖直向上;对整个模型添加重力载荷约束。磨杆整体通过螺钉将套筒右端面与床身相连接,故将套筒右端面设为固定端,施加Fixed Support 约束。主轴的变形和等效应力分布情况分别如图3、图4 所示,最大变形处为砂轮轴端,变形量为0.245 mm,符合悬臂梁端部变形规律;最大应力位置为主轴与前端轴承接触区域,大小为97.265 MPa,远低于主轴材料9Mn2V 的屈服强度极限。
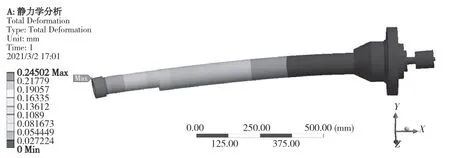
图3 磨杆静力学仿真变形图Fig.3 Deformation diagram of internal grinding tool
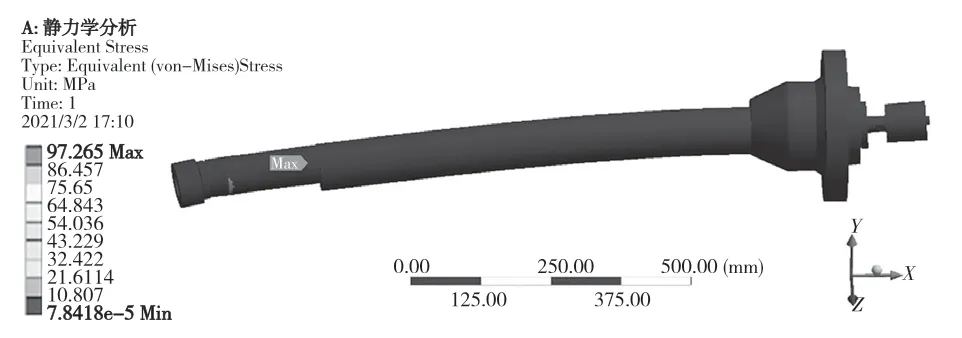
图4 磨杆静力学仿真应力图Fig.4 Stress diagram of internal grinding tool
2.2 静态特性实验
对磨杆进行静刚度实验。将其安装固定到内圆磨床床身上,套筒末端固定。磨床处于关闭状态,分别在法兰盘砂轮安装面上悬挂大小为49 N,98 N,147 N 的载荷,使用千分表测量磨杆前端部的位移变形量,实验原理如图5 所示。
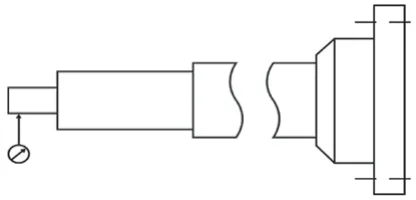
图5 静特性实验原理图Fig.5 Schematic diagram of static characteristic test
在磨杆有限元模型砂轮磨削面分别施加49,98,147 N 载荷,方向与重力方向相同,其余边界条件不变,分别进行静力学仿真求解,磨杆前端变形量结果如表2 所示。
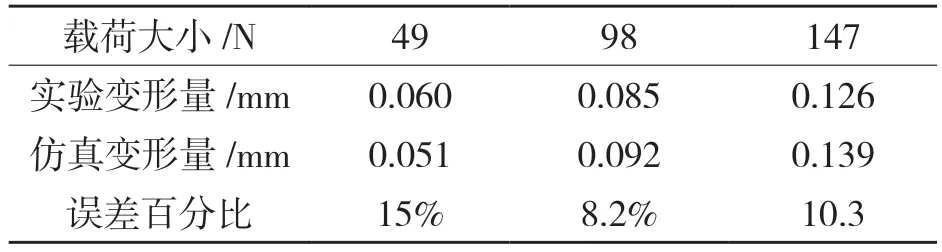
表2 实验与仿真磨杆最大变形量Tab.2 The maximum deformation of experiment and simulation
由表2 知,磨杆静态分析实验结果与仿真结果最大误差为15%,说明有限元模型的合理性。
3 磨杆动态特性分析
3.1 模态分析
3.1.1 模态分析的概念
模态分析就是确定机械结构的振动特性,得到结构的固有频率和振型。对复杂结构进行模态分析不仅为系统的振动特性分析、振动故障诊断及动态特性的优化设计提供依据,还可以确定特定方向上的振动幅度,避免结构发生共振[4]。
结构的低阶固有振型要比高阶固有振型对结构的振动影响大,因此低阶振型对磨杆的动态特性起决定性作用,所以在对磨杆进行模态分析时只需对其前几阶振型进行分析。
3.1.2 模态分析的求解
与静态分析相似,在模态分析时也应将套筒右端面设为固定约束。图6—图11 分别为求解计算后得到的磨杆前6 阶模态固有频率和振型。各阶固有频率和振型如表3 所示。

图6 1 阶振型Fig.6 First order vibration shape

图7 2 阶振型Fig.7 Second order vibration shape

图8 3 阶振型Fig.8 Third order vibration shape

图9 4 阶振型Fig.9 Fourth order vibration shape

图10 5 阶振型Fig.10 Fifth order vibration shape

图11 6 阶振型Fig.11 Sixth order vibration shape

表3 模态分析结果Tab.3 Results of modal analysis
3.1.3 实验模态分析
将磨杆简化为悬臂梁,在Modal View 模态分析软件中建立磨杆的结构模型。如图12 所示,沿X 方向(磨杆的轴向)均匀布置1~5 共5 个测点,其中1 点为悬臂端,5 点为固支端。
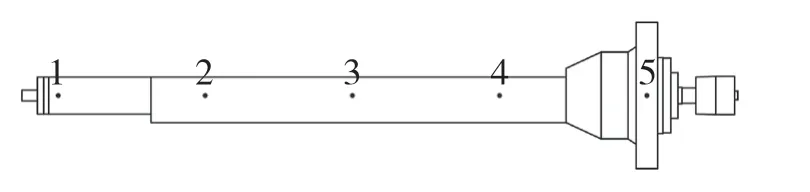
图12 模态实验示意图Fig.12 Sketch map of modal experiment
采用响应点移动-激励点固定的锤击法对磨杆进行模态测试,使用NI 9234 采集模块的cDAQ-9172 采集系统进行数据采集,完成磨杆实验数据的采集之后,利用Modal View 进行模态参数辨识,提取分析带宽内所关心的固有频率和模态振型。通过实验模态测试获得磨杆的固有频率为64.5 Hz,对应的共振转速3 870 r/min。由表3可知,磨杆动态仿真的1 阶固有频率为68.0 Hz,对应的共振转速4 080 r/min,二者结果误差仅为5.4%,说明有限元模型的准确性。
3.2 谐响应分析
磨杆进行磨削精加工时,由于砂轮和被加工工件表面间的相互作用会产生简谐力并作用于整个系统,当磨杆的固有频率和动态磨削力的频率相一致时,系统就会产生共振,会造成较大变形,影响加工精度。在磨杆工作时,要避免这种情况发生[5]。谐响应分析是在模态分析的基础上进行的,对磨杆进行谐响应分析可以直观地分析在动态磨削力干扰下它的抗振性能[6]。
利用 ANSYS Workbench 谐响应分析模块对磨杆进行响应,激振力作用在砂轮面上,分别为沿Z 轴正方向200 N 和沿Y 轴负方向60 N,激励频率区间为60~400 Hz,设置50 个频率采样点。由于主轴变形直接影响砂轮磨削精度,所以谐响应分析取主轴为分析对象,对X,Y,Z 方向分别进行响应位移计算,结果如图 13—图15 所示。
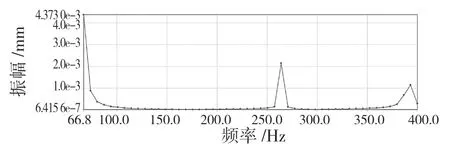
图13 X 方向上的谐响应曲线Fig.13 Harmonic response curve in X direction
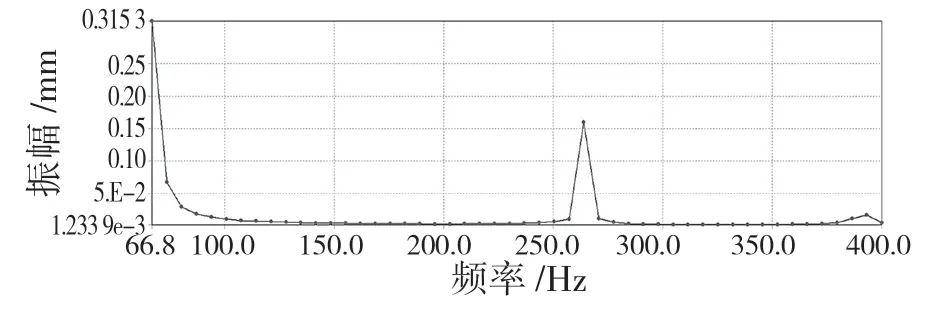
图14 Y 方向上的谐响应曲线Fig.14 Harmonic response curve in Y direction
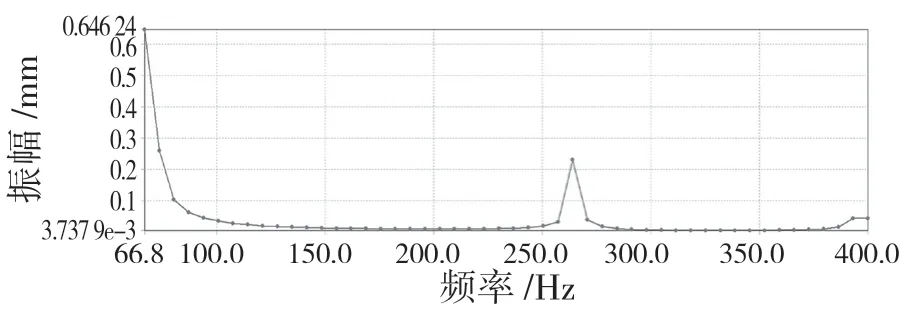
图15 Z 方向上的谐响应曲线Fig.15 Harmonic response curve in the Z direction
结果表明,频率在 65,260,390 Hz 附近时主轴振幅较大,会发生共振,与上文模态分析结果一致。其中Y 轴方向最大振幅为0.646 mm,如果发生共振会对加工精度造成影响。
4 结论
本文运用ANSYS Workbench 对磨杆系统分别进行静力分析与模态分析,为了得到更加精确的分析结果,按照实际工况对模型施加约束载荷,并考虑结构重力影响,还通过静刚度实验与测试模态实验分别验证静、动力学仿真结果的准确性。结论如下:
(1)磨杆在真实工况下砂轮端变形量最大,为0.245 mm;最大等效应力处位于主轴前端与轴承接触区域,为97.265 MPa,远小于主轴材料9Mn2V 的屈服强度极限。
(2)磨杆前6 阶固有频率范围为68.037~396.660 Hz,1 阶共振转速为4 082 r/min,与磨杆设计转速区间2 000~5 000 r/min 相重叠。应对磨杆进行结构优化设计,避免工作中引起共振。
(3)通过对磨杆主轴进行谐响应分析得到发生共振时的曲线,可以直观地看到主轴各方向响应位移随激励频率变化的规律。
(4)静动态分析中磨杆的受力与变形情况为后续该类型磨杆结构改进优化设计提供了参考。
