高碱煤燃烧初期羧酸钠的迁移转化机理

樊俊杰，张 蓓，徐 达，杨 柳

(上海理工大学环境与建筑学院，上海 200093)

我国新疆维吾尔族自治区煤炭资源储量极为丰富，已探明总储量高达2.19 万亿吨，是全国总煤炭储量的40%[1].新疆煤碱金属钠含量高，属于典型的高钠煤，在实际工业应用中会导致水冷壁结渣严重，水平烟道沾污积灰严重等问题，限制了其大规模利用，但另一方面煤中的碱金属钠对煤燃烧过程具有催化作用[2].煤中钠的赋存形态主要为水溶态、醋酸铵溶态、盐酸溶态及不溶态[3].煤中钠的释放过程可分为燃烧初期和后期两个阶段，而不同赋存形态钠的相互转化主要发生在燃烧初期，仅有少量挥发到气相.Li等[4]对维多利亚褐煤中钠进行了研究，发现醋酸铵溶钠对煤热解影响最大.陈川等[5]和Jiao 等[6]在研究准东煤的燃烧过程时，发现以醋酸铵溶钠为主的有机钠对煤燃烧有促进作用.因此，认识羧酸钠对高碱煤燃烧初期的影响规律和机理对新疆高碱煤的高效利用具有重要意义.

大量研究人员研究了羧酸钠在低阶煤燃烧初期的作用.实验表明，在热解过程中，羧酸钠的理化形式会随着温度的升高而变化.Harry 等[7]发现褐煤热解过程中二氧化碳的生成量与煤中羧基的含量成正比，表明煤热解过程中二氧化碳主要由羧基脱羧反应生成.Quyn 等[8]发现，随着燃烧反应的进行，焦炭表面钠出现积聚，形成“C—O—Na”结构.邓加晓等[9]在研究高碱煤在燃烧初期钠的迁移规律时发现，当热解温度低于600 ℃时，产生的轻质羧酸钠会释放到气相中，随着温度升高，羧酸钠分解生成CO2，同时钠原子会与煤焦基体结合.近年来，量子化学模拟计算的发展为研究者们在微观上对实验现象进行解释、预测提供了一个新的方法.通过量子化学方法计算可为分析煤结构中的反应活性位点提供理论指导.Mudedla 等[10]选择了几种小分子带有单一的含氧官能团的类煤结构化合物，对反应路径进行了量子化学计算，解释了水分子在煤热解过程中发挥的促进作用：水分子作为质子供体能够有效地降低脱羧反应与酯化反应的活化能.Li 等[11]设计不同化学环境下的小分子类煤结构模型化合物，计算得到化合物中化学键的键解离能，总结出烷基侧链与醚键是最容易发生化学键均裂的活性位点.贾建波等[12]利用量子化学密度泛函理论方法，对甲基苯热解生成甲烷的机理进行了热力学和动力学的计算，结果表明在生成甲烷的所有反应路径中，其控速步骤是甲基苯的脱氢或者脱甲基过程.

综上所述，尽管近几年的研究对理解含钠化合物在燃烧初期的作用做出了重大贡献，但由于系统的复杂性，在高碱煤的初级热解过程中与羧酸钠相关的机理研究仍不够全面.本研究选择三元环Zigzag 边缘模型，利用密度泛函理论对煤中羧酸钠的迁移转化过程进行量子化学计算，从单分子反应、双分子反应及与自由基反应3 个方面详细分析其可能的反应路径，并从动力学角度进行比较分析，进而从分子水平上揭示高碱煤燃烧初期羧酸钠最易发生反应的途径.

1 模型选择及计算方法

1.1 分子结构模型的选择

煤焦模型是由3 至7 个六元环组成的单层石墨烯模型[13].基于Zigzag 焦炭模型的几何参数与实验参数一致性，Zigzag 型结构通常被用作计算的理想模型[14].有研究表明Zigzag 型结构在焦炭的边缘原子活性位置上存在很高的活性，大部分燃烧反应发生在焦炭的边缘.由于高碱煤多为低阶煤，平均芳环数3环及以下，因此，本文采用改进的三元锯齿形结构作为含碳模型，采用CM—COONa 结构作为醋酸溶钠模型，CM—COOH 和CM—OH 为与CM—COONa进行双分子反应的结构.具体的模型结构如图1所示.

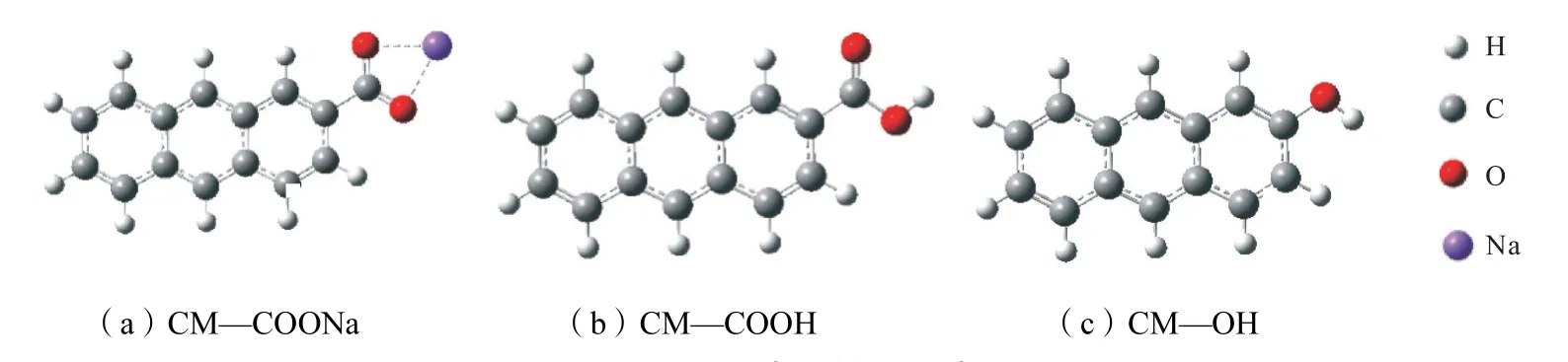
图1 煤焦表面模型示意Fig.1 Schematic diagram of coal char surface model

1.2 计算方法

本研究基于过渡态原理和密度泛函理论(DFT)，采用量子化学软件Gaussian 09 程序[15]进行反应路径计算.计算方法和基组的选取直接决定了量子化学计算的精度和耗时.M06-2X 泛函[16]可以合理描述色散作用，并获得更可靠的过程能垒.相比B3LYP 而言，可以更有效地用于描述金属与有机化合物之间的反应[17].因此，中间体和过渡结构的优化和频率分析都是在无限制的M06-2X 方法和6-311g(d)基组上进行的，所有计算都在稳定结构的基态下进行.活化能Ea由Arrhenius 方程线性化确定，即ln k 与1/T 成线性关系.对数阿伦尼乌斯公式见式(1)：

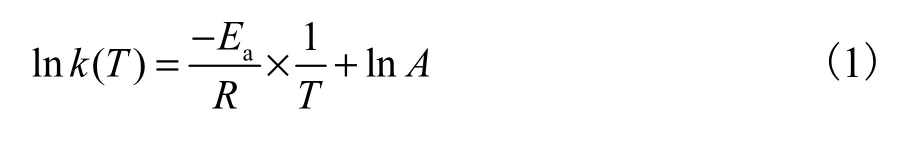
根据经典过渡态理论(conventional transition state theory，cTST)，反应速率常数计算公式如下：

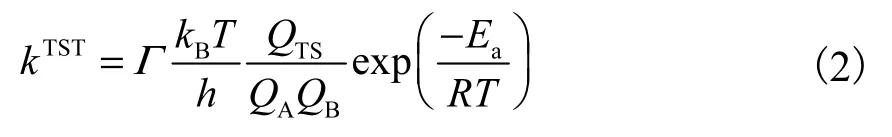
式中：Г 为量子隧道修正系数；Ea为反应势垒，kJ/mol；R 为气体摩尔常数，J/(mol·K)；T 为温度，K；kB为玻尔兹曼常数，J/K；h 为普朗克常数，J·s；QTS、QA和QB依次为过渡态TS 和反应物A 和反应物B 的配分函数.

式中：νm为反应路径振动的虚频值，cm-1；c 为光速，m/s.

2 结果与讨论

本节主要讨论了类煤模型化合物CM—COONa在燃烧初期的单分子反应、双分子反应以及与自由基的反应路径.

2.1 CM—COONa在燃烧初期的单分子反应

图2 给出了CM—COONa 分子在燃烧初期的两条反应路径，图3 为对应的反应能垒图.其中“R”表示反应物，“IM”表示反应中间体，“TS”表示反应过渡态，“P”表示反应产物.

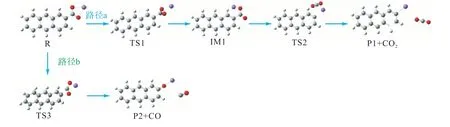
图2 CM—COONa分子在燃烧初期的反应路径Fig.2 Reaction path of CM—COONa molecules in the initial stage of combustion

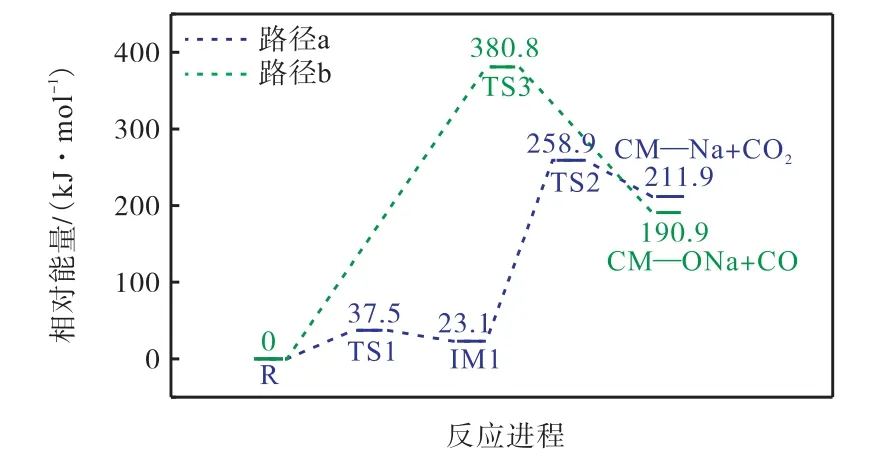
图3 CM—COONa分子在燃烧初期的反应能垒图Fig.3 The reaction energy barrier of CM — COONa molecule in the early stage of combustion

路径a 是CM—COONa 逐步脱羧生成CM—Na和CO2，首先，CM—COONa 中的CO2基团通过TS1扭曲约36°形成反应前驱体IM1，R→TS1 需克服37.5 kJ/mol 的能垒.随后，该前驱体中C—C 键断裂形成过渡态TS2，与钠离子的键分散了一些负电荷，并且阳离子通过与分离组分键合来稳定过渡态几何结构，此时需克服235.8 kJ/mol 的能垒，最终生成CM—Na 和CO2，其中脱羧的第2 步是速率决定步骤.路径b 是直接去羰基化生成CM—ONa 和CO，需克服380.8 kJ/mol 的能垒.显然，相比于路径b，路径a 的反应更容易发生.这与Harry 等[7]的实验现象相吻合.

2.2 CM—COONa 在燃烧初期的双分子反应

CM—COONa 和相关模型化合物(CM—COOH和CM—OH)在燃烧初期会发生双分子催化分解(脱羧和脱碳化)和交联.基于上述反应方案，考虑了9种可能的反应路径.

2.2.1 CM—COONa 与CM—COONa

图4 给出了CM—COONa 与CM—COONa 的反应路径图，3 条路径分别显示了CM—COONa 二聚体的脱羧、脱碳和交联.图5 为对应的反应能垒图.首先，CM—COONa 二聚体放出65.1 kJ/mol 的热量形成稳定的反应复合物IM1，路径c 为催化脱羧过程，第1 个CM—COONa 的钠阳离子对第2 个CM—COONa 的C5 原子亲电攻击导致C5～C8 键的裂解而位移.在第2 个CM—COONa 模型中CO2分离后，发生Na—Na 交换形成CM—COONa，该反应需要克服152.7 kJ/mol 的能量.路径d 为Na—H 交换模型化合物催化脱碳.这一过程需要克服301.9 kJ/mol 的能量.路径e 发生的是羧酸钠与羧酸基团之间的交联，该反应生成了酸酐和氧化钠加成物.有研究表明，脱羧反应是发生热交联过程的主要因素[18-19].然而也有文献报道，羧基的脱水和酯化有助于低温交联[20].通过比较各反应的势垒高度，可以明显看出路径c 最容易发生，而路径e 即羧酸钠之间的交联反应最难发生.

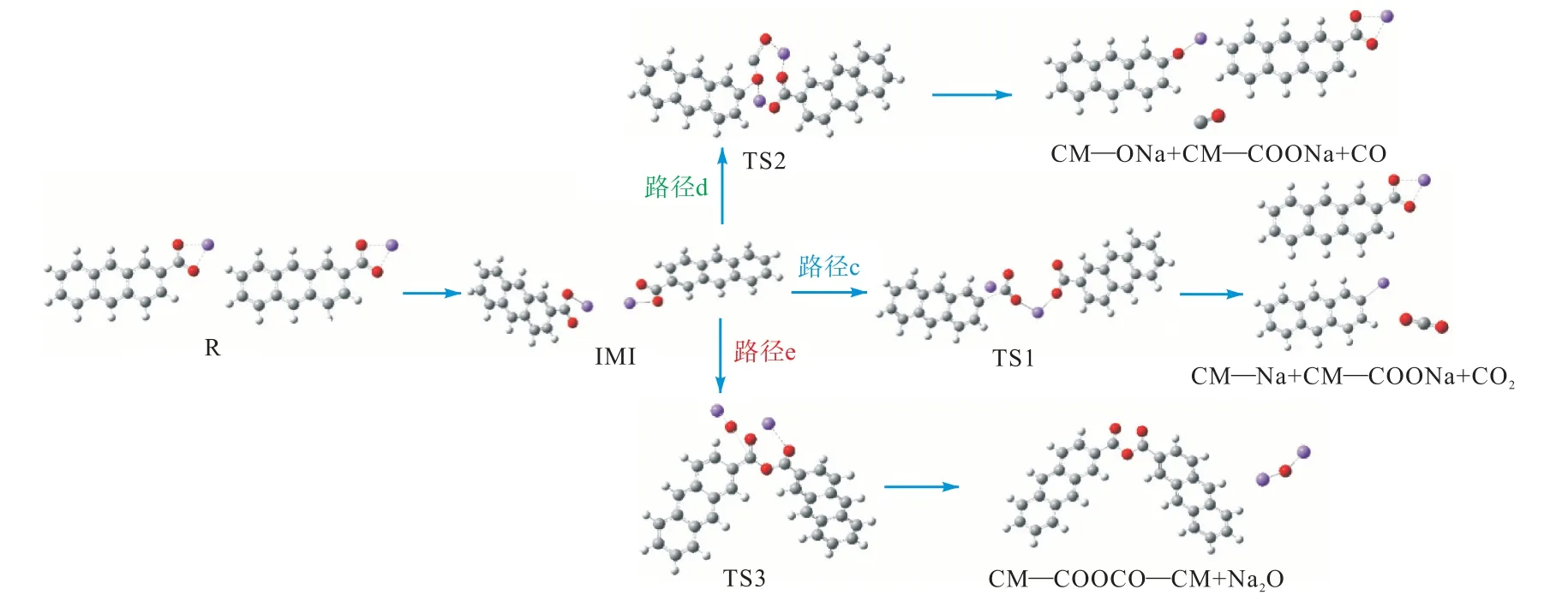
图4 CM—COONa与CM—COONa的反应路径Fig.4 Reaction path of CM—COONa and CM—COONa

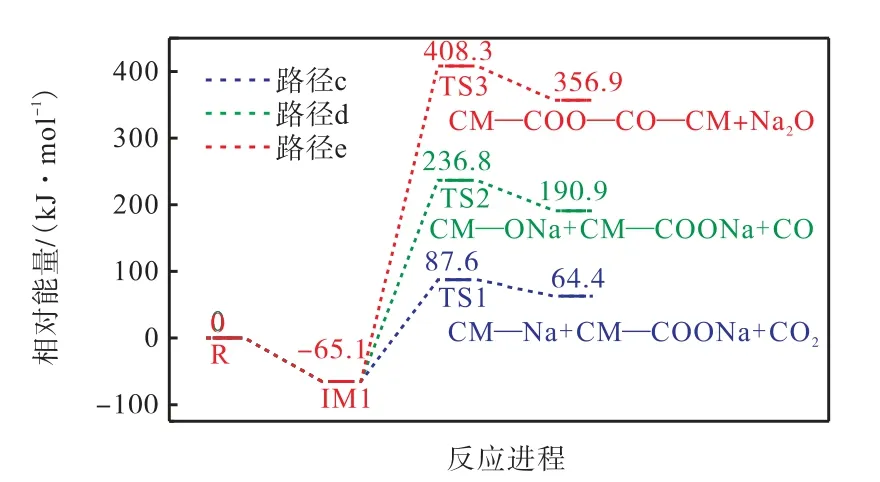
图5 CM—COONa与CM—COONa的反应能垒图Fig.5 Reaction energy barrier diagram of CM—COONa and CM—COONa

2.2.2 CM—COONa 与CM—COOH

图6 给出了CM—COONa 与CM—COOH 的反应路径图，图7 为对应的反应能垒图.从图中可以看出，路径g 是在相邻羧基钠通过Na—H 交换下，模型化合物脱羧，从而释放 C O2.该反应需要克服221.1 kJ/mol 的能量.路径h 为Na—H 交换模型化合物催化脱碳.这一过程需要克服244 kJ/mol 的能量.路径f 发生的是羧酸钠与CM—COOH 之间的交联，CM—COONa 的C—O 键及CM—COOH 的C—O键断裂克服381 kJ/mol 能垒形成NaOH.通过比较各反应的势垒高度，可以明显看出路径g 最容易发生，而路径h 即羧酸钠与CM—COOH 之间的脱碳反应最难发生.

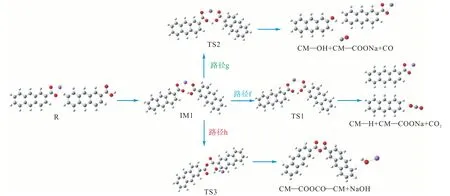
图6 CM—COONa与CM—COOH的反应路径Fig.6 Reaction path of CM—COONa and CM—COOH

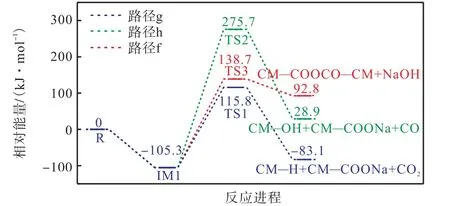
图7 CM—COONa与CM—COOH的反应能垒图Fig.7 Energy barrier diagram of CM—COONa and CM—COOH

2.2.3 CM—COONa 与CM—OH

图8 为燃烧初期CM—COONa 与CM—COOH的反应路径图，图9 为其反应能垒图.从图中可以看出，羧酸钠通过Na—H 交换的催化脱羧和脱碳反应通过过渡态TS1 和TS2 进行.这两条路径的过渡态TS1、TS2 所克服的能垒分别为141.5 kJ/mol 和247.9 kJ/mol.路径k 为CM—COONa 和CM—OH发生的酯化交联反应，该反应的机理是通过CM—COONa 的Na 阳离子与CM—OH 的羟基以及C—O键的形成(即在酯基中)，克服了187.5 kJ/mol 能垒形成NaOH.上述3 种双分子反应的比较表明，最低能量路径是路径i 催化脱羧.

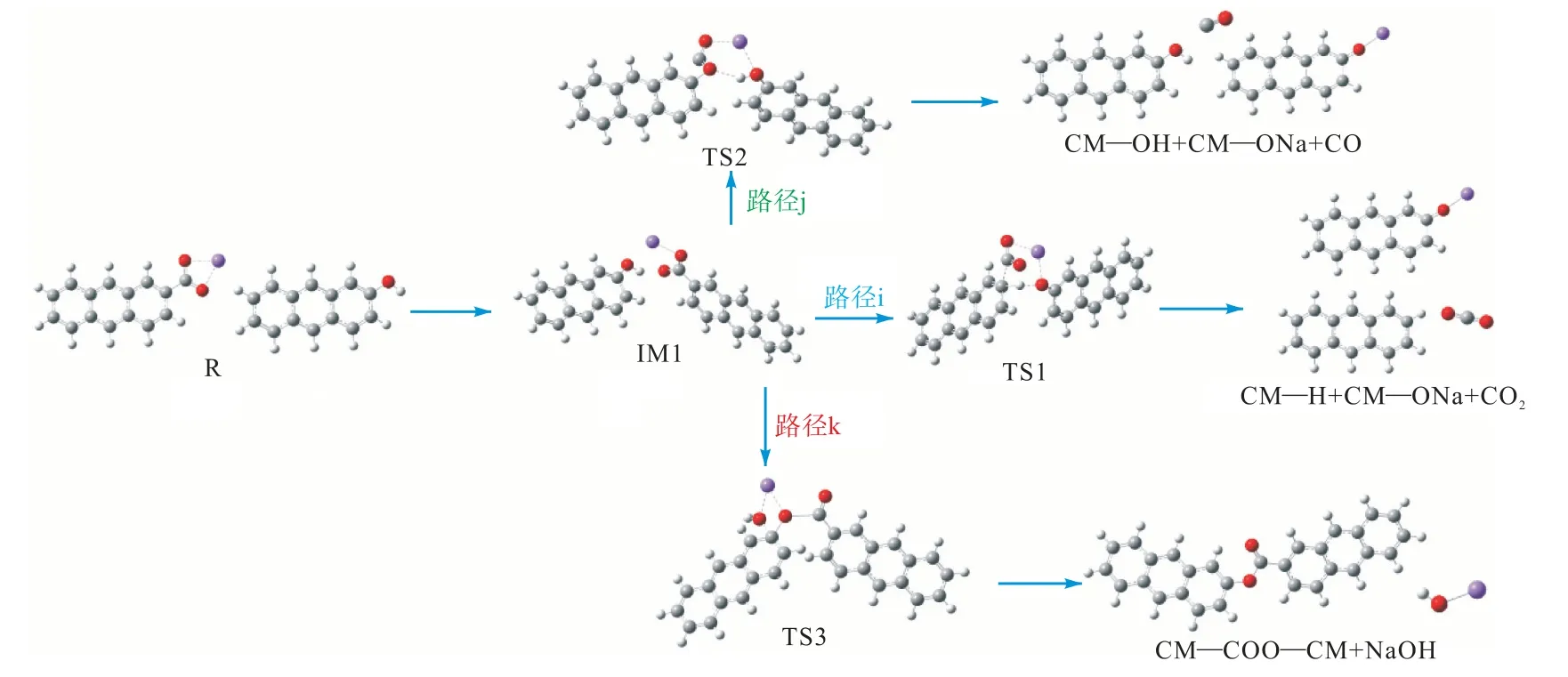
图8 CM—COONa与CM—OH的反应路径Fig.8 Reaction path of CM—COONa and CM—OH

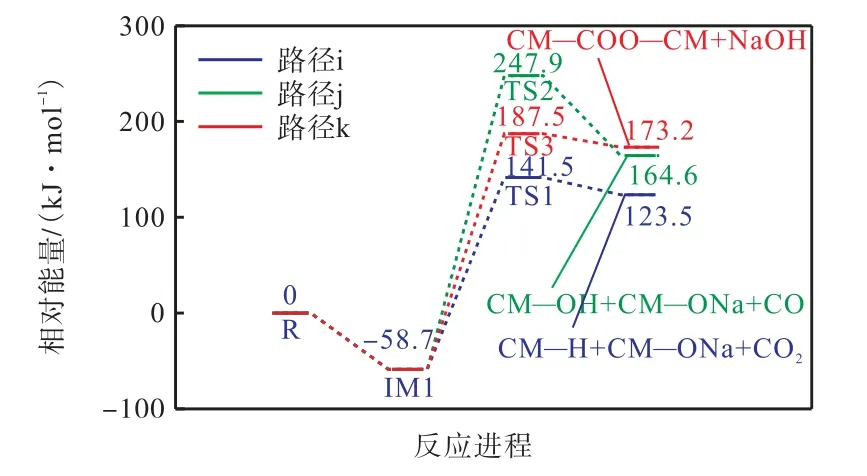
图9 CM—COONa与CM—OH的反应能垒Fig.9 Energy barrier diagram of CM — COONa and CM—OH

2.3 CM—COONa在燃烧初期与自由基的反应

2.3.1 CM—COONa 与H·

在羧酸钠基团分解之前，煤基质中固有的弱键在加热后可能会发生热解，产生自由基.然而，固体煤基质由于空间位阻，芳香环框架上的自由基位点在煤中得到了很好的分离，因此与羧酸钠基团结合并不容易.只有H 和CH3等小自由基才能很容易地渗透到煤基质中并在热解过程中与羧酸钠基团结合[21].因此，在本研究中主要关注H 自由基和CH3自由基与羧酸钠基之间的反应.

图10 给出了CM—COONa 在燃烧初期与H 自由基的反应路径，图11 给出了其反应能垒图.从图中可以看出，从反应物到3 种反应复合物IM1、IM2、IM4 的形成都是放热的，吸附能分别为-7.4 kJ/mol、-4.8 kJ/mol 和-9.7 kJ/mol，这意味着系统可以通过碰撞来稳定，且这3 个值非常接近，表明H 自由基没有强烈的首选吸附位点.路径l 为羧酸钠中的Na 与H自由基发生 N a—H 交换进行，克服的能垒为15.2 kJ/mol.此外，H 自由基还可以攻击羧酸盐的C8形成甲酸钠分子(路径m)或攻击芳香族C5 形成Na和CO2(路径n).计算表明，这两种反应都是通过逐步加入—消除机制进行的.路径m 的速率决定步骤为反应的第1 步，该步骤克服反应能垒56.7 kJ/mol.而路径n 以类似路径m 的方式发生，但第1 步是在芳香族C5 原子中加入H 自由基，第2 步为NaCO2自由基的形成，随后在二次反应中，自由基会分裂成Na 原子和CO2分子，该路径的速率决定步骤为反应的2 步，克服反应能垒60.4 kJ/mol.上述3 种双分子反应的比较表明，最低能量路径是路径l.

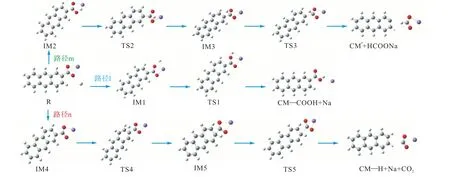
图10 CM—COONa与H·的反应路径Fig.10 Reaction path of CM—COONa with H·

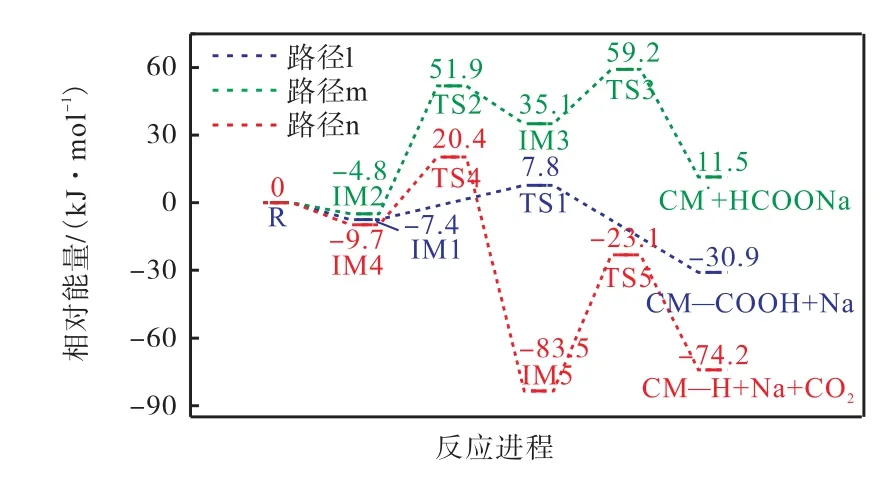
图11 CM—COONa与H·的反应能垒图Fig.11 Reaction energy barrier diagram of CM—COONa with H·

2.3.2 CM—COONa 与·CH3

图12、图13 分别给出了CM—COONa 在燃烧初期与 CH3自由基的反应路径图及其反应能垒图.如图所示，CH3自由基和CM—COONa 之间的反应路径与H 自由基和CM—COONa 有一些相似之处.可以看出，在M06-2X/6-311G(d)水平上计算，反应复合物IM1、IM2 的能量几乎相同，这表明CH3自由基没有强烈的首选吸附位点.路径o 中CH3自由基与O 结合，释放Na 原子，克服125.3 kJ/mol 的能垒.路径p 的速率决定步骤克服117.6 kJ/mol 能垒，生成乙酸钠.路径q 在TS4 处有70.7 kJ/mol 势垒，该步骤为速率决定步骤，远远低于路径o 和路径p，表明路径q 更容易发生反应.

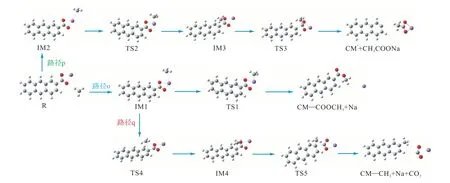
图12 CM—COONa与·CH3 的反应路径图Fig.12 Reaction path of CM—COONa with ·CH3

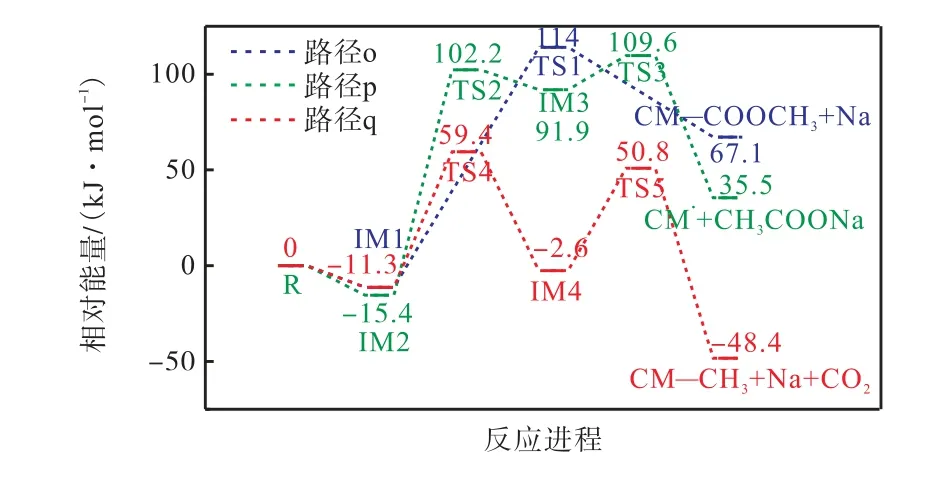
图13 CM—COONa与·CH3 的反应能垒图Fig.13 Reaction energy barrier diagram of CM—COONa with ·CH3

2.4 动力学分析

为了进一步理解反应发生的难易程度，本研究计算了反应速率常数，如图14 所示，随着温度的升高，反应速率常数也在逐渐增大，表明高碱煤燃烧初期羧酸钠的迁移转化有较强的温度依赖性.在298.15～1 400 K 温度范围内比较路径b 和路径n 的反应速率常数，可以看出路径b 比路径n 决速步的反应速率常数至少高40 个数量级，且1 400 K 时基元反应路径b(R→CM—ONa＋CO)的lnk 仍小于0，这表明CO2分子更倾向于通过路径n 脱附出去.拟合得到各路径反应动力学参数见表1，由表1 可知，CO2分子通过路径n 脱附的活化能远低于通过其他路径的活化能，同样表明CM—COONa 在燃烧初期与H 自由基的反应更容易发生.

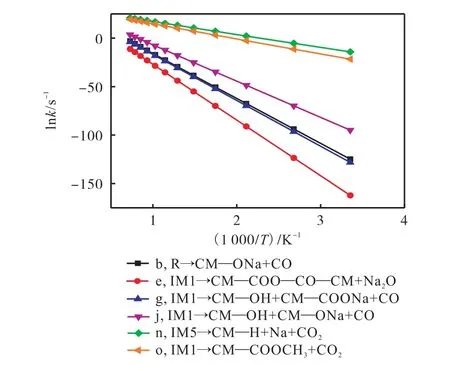
图14 各反应路径决速步反应速率常数Fig.14 Rate constant k calculated from cTST

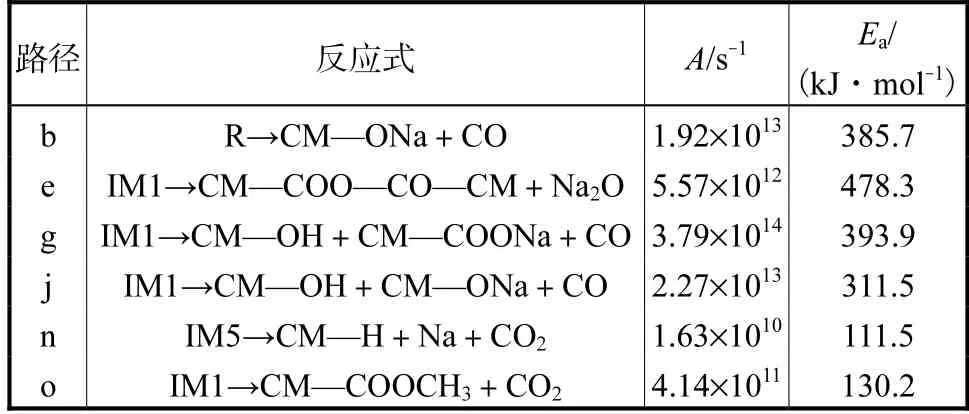
表1 各路径反应动力学参数Tab.1 Fitted kinetic parameters of Arrhenius expressions

3 结论

利用密度泛函理论研究了高碱煤燃烧初期羧酸钠的反应机理，提出了关于羧酸钠的单分子直接脱羧和脱碳化，与邻近官能团可能发生的双分子反应，包括脱羧、脱碳化和二聚体羧酸钠基团的交联反应，以及与H 和CH3自由基的反应路径.

(1) 高碱煤燃烧初期羧酸钠单分子脱羧以释放二氧化碳为首选热解途径，其克服的反应能垒为235.8 kJ/mol，小于生成CO 路径所克服的能垒.

(2) 羧酸钠和相关模型化合物(CM—COOH 和CM—OH)在燃烧初期发生的双分子脱羧反应需翻越的能垒较脱碳反应和交联反应的能垒低，其中路径c中能垒最低，为152.7 kJ/mol，即双分子脱羧最易进行.

(3) 羧酸钠与H 自由基和甲基自由基发生反应，这些自由基可以降低高碱煤基质中羧酸钠基的热解活化能，导致Na 原子和NaCO2自由基的释放.