脉冲X射线衍射法测量冲击加载下的晶格形变量

唐 波，黑东炜，马 戈，夏惊涛，盛 亮，魏福利，罗剑辉，李运良，谭书舜

(强脉冲辐射环境模拟与效应国家重点实验室，西北核技术研究所，陕西 西安 710024)

冲击现象在自然界广泛存在，然而目前对于冲击波在固体内的传播过程以及冲击加载下材料的动态响应尚不能完全地认识和理解，重要原因是缺乏高时空分辨的原位诊断技术。在瞬态冲击载荷下，晶体在微观层面会发生一系列的变化，包括可逆的晶格弹性形变、不可逆转的位错成核、运动或晶体结构变化造成的塑性形变、熔化、相变等，这些微观响应对材料宏观层面的行为会产生直接而又巨大的影响[1]。目前，冲击载荷作用下材料的瞬时晶格状态缺乏直观的实验数据。在实验研究中，主要发展形成了冲击样品回收分析技术[2-3]和宏观在线测量技术[4-5]，前者对冲击回收样品进行微观结构分析，从而推测判断样品动力学行为，但无法实现动力学加载下的实时测量；后者如激光干涉技术、埋入式石英传感器等，对冲击材料的宏观行为进行在线测量，但无法提供动力学加载下材料晶格层面的信息。因此，现有的实验测量技术难以同时满足实时和微观两个需求，研究可在微观层面上实时观测材料冲击响应的诊断方法十分重要。

脉冲X射线衍射测量技术是获取冲击加载下材料瞬时原子层面信息最直接的实验方法[6-10]。材料瞬时微观结构通过X射线衍射效应直接反映在衍射图像中，通过分析衍射图像的特征信息(衍射束方向、衍射谱形状及衍射强度)，可获得丰富的晶体微观结构信息，如晶格形变量、微观缺陷状态等。本文针对脉冲X射线衍射法测量冲击加载下晶格形变量的定量化问题进行研究，建立测量模型，分析晶格形变量测量的不确定度来源，给出冲击加载实验中LiF晶体的衍射测量结果并进行讨论。

1 测量原理及模型

根据布拉格公式可知，已知波长的X射线束入射单晶材料发生衍射时，晶体晶面间距和X射线衍射角之间存在唯一对应关系。当晶体材料受到瞬时冲击载荷作用时，处于冲击压缩状态的晶体晶格结构发生变化，相应地冲击状态下晶体的衍射角与静态相比也会发生变化，如图1所示。衍射角改变量Δθ与晶面间距变化量Δd的关系为：

(1)

式中：d0和θ0分别为初始晶面间距和初始衍射角；Δd/d0为晶格形变率。通过测量材料晶格形变导致的衍射峰偏移量Δxdef，就可获得衍射角改变量Δθ，从而得到晶格形变信息。X射线光源S发出的单色X射线束应具有一定的发散度，可满足未形变晶体静态衍射角θ0和冲击形变晶体动态衍射角θ0+Δθ的变化。由图1可知，当成像探测器平面与静态晶体的衍射光束垂直时，Δθ与Δxdef的关系为：

Δxdef=(L0+L1)tan Δθ

(2)

式中：L0为X射线光源S到晶体表面静态衍射点的距离；L1为晶体静态衍射点到探测器平面的距离。由此可见，精确测量衍射峰的偏移量是准确获取压缩形变状态下晶体晶格参数的保证。

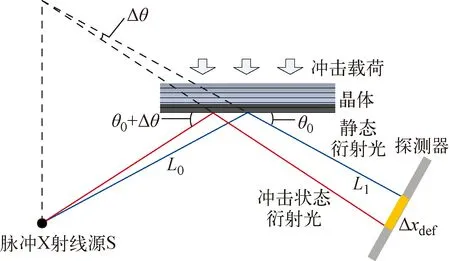
图1 脉冲X射线衍射测量光路图Fig.1 Light path for pulsed X-ray diffraction measurement

轻气炮是开展冲击加载实验的一种有效的技术途径，它能发射平面飞片，使其与待测晶体样品撞击，在晶体样品中产生瞬态高压-高温状态。在轻气炮加载条件下开展晶体晶格形变的X射线衍射测量过程中，除去晶格形变引起的衍射峰偏移外，测得的衍射峰偏移量Δxmeasured中还包括飞片与晶体撞击倾斜造成的衍射峰偏移Δxtilt和晶体测量点宏观位移造成的衍射峰偏移Δxtrans，如图2所示，则有：

Δxmeasured=Δxdef+Δxtilt+Δxtrans

(3)

飞片与晶体撞击倾斜是指在轻气炮驱动的平面冲击加载实验中飞片在加速过程中可能会发生倾斜，而后与晶体样品撞击使得晶体也发生倾斜。该倾斜度会对晶格形变测量造成影响，如图2a所示。当飞片以速度v、倾斜角度φ与晶体碰撞时，造成的晶体倾斜角θtilt为：

(4)

式中，up为晶体后界面处的粒子速度。

如果沿光路传播方向光源到晶体与晶体到探测器的距离相等时，晶体倾斜不会造成探测器上衍射条纹发生位移，此位置为探测面的理想位置。而探测面偏离理想位置时，晶体倾斜会造成探测面上衍射峰的偏移。假设探测面与未倾斜晶体的衍射光束垂直，探测面偏离理想位置的距离为l，则有：

Δxtilt=l·tanθtilt

(5)

晶体测量点宏观位移是指脉冲X射线曝光起始时刻tX-ray在冲击波到达晶体样品背表面的时刻t0后，在时间间隔[t0,tX-ray]中，晶体会沿冲击波传播方向出现宏观位移，如图2b所示。当探测面与晶体的动态衍射光束垂直，晶体宏观位移量为tmov时，因晶体宏观位移造成的衍射峰偏移量Δxtrans为：

Δxtrans=2tmovcosθs

(6)

式中，θs为冲击状态下的衍射角。晶体宏观位移量tmov为：

tmov=(tX-ray-t0)up

(7)

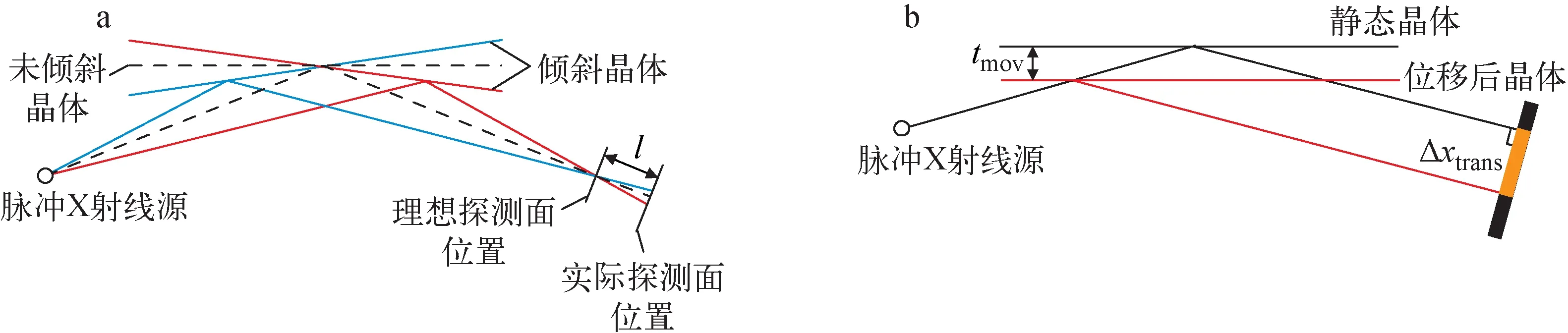
a——飞片与晶体撞击倾斜的影响；b——宏观位移的影响图2 飞片撞击倾斜及晶体宏观位移对脉冲X射线衍射测量的影响Fig.2 Influence of pulsed X-ray diffraction measurement on impact tilt and translation of lattice

综上所述，在实验测得的衍射峰位移的基础上，应扣除Δxtilt和Δxtrans的影响，而后得到的衍射峰位移量方可认为是由晶体晶格形变所造成的。

2 不确定度分析

考虑系统测量晶格形变率Δd/d0的合成不确定度。根据式(1)和不确定度传递规律可知，晶格形变率的不确定度u(Δd/d0)与衍射角变化量的不确定度u(Δθ)的关系为：

(8)

根据式(2)和不确定度传递规律可知，衍射角变化量的不确定度ux(Δθ)与Δxdef的不确定度u(Δxdef)的关系为：

(9)

由于Δxdef与L0+L1相比为小量，因此，式(9)可写为：

(10)

根据式(3)和不确定度传递规律可知：

u(Δxdef)=

(11)

式中：u(Δxmeasure)为衍射峰偏移量测量值的不确定度，主要来自于衍射峰位读出的不确定度，包括静态衍射峰和动态衍射峰；u(Δxtilt)为撞击倾斜导致的衍射峰偏移量不确定度；u(Δxtran)为晶体宏观位移导致的衍射峰偏移量的不确定度。

由于实验中未监测撞击平面度，取撞击倾斜度φ=5×10-4rad[11]作为极限误差。根据式(5)可知：

(12)

根据式(6)可知晶体宏观位移导致的衍射峰偏移量的不确定度u(Δxtran)为：

u(Δxtrans)=2cosθs·u(tmov)

(13)

式中，u(tmov)为晶体宏观位移的不确定度。由于X射线曝光时刻的测量不确定度为亚ns量级，因此，主要考虑冲击波到达晶体样品背表面的时刻t0的测量不确定度，即u(tmov)=u(t0)。t0是利用压电探针测量得到，综合考虑探针安装工艺、响应时间及冲击波阵面形态等因素，取t0的测量不确定度为u(t0)=10 ns。

3 典型实验结果及讨论

3.1 脉冲X射线衍射测量实验结果

在西北核技术研究所口径57 mm的一级轻气炮上开展了平面冲击加载下LiF(100)晶体晶格响应的脉冲X射线诊断实验，图3为轻气炮加载下单晶体的脉冲X射线衍射测量布局图。轻气炮驱动的撞击飞片材料为6061-T6 Al，飞片直径为56 mm，厚度为3 mm。实验采用的脉冲X射线源为Scandiflash AB公司的TD-450S系统，输出的X射线脉冲宽度为25 ns。X射线管采用的阳极材料为Mo，Kα线对应的LiF(100)晶体的静态衍射角θ0为10.17°。X射线成像探测器为富士公司的成像板，空间分辨率为100 μm。LiF(100)晶体为圆片状，直径为20 mm，厚度为1 mm。为延长LiF晶体中X射线探测区域的冲击高压状态持续时间，在LiF晶体的背表面放置冲击阻抗低、原子序数小的非晶材料，实验中采用的Alfa Aesar公司的I型VitreousCarbon(VC)，厚度约1 mm。

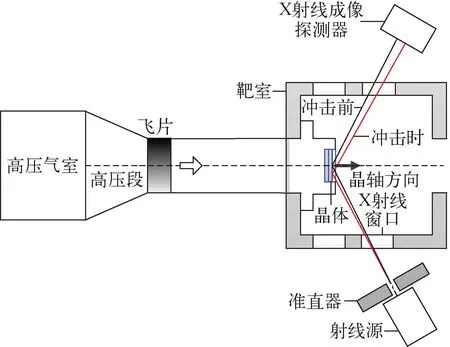
图3 轻气炮加载下单晶体的脉冲X射线衍射测量布局图Fig.3 Schematic diagram of pulsed X-ray diffraction of single crystal under gas gun loading

图4为撞击速度为492 m/s时所获得的LiF晶体的静态及冲击状态的脉冲X射线衍射结果。图4b是对图4a中垂直像素段[1 400,1 459]的衍射数据进行累加得到的。

3.2 实验结果分析

对垂直像素段[1 400,1 459]的衍射条纹进行分段累加处理，得到不同像素段的衍射线如图5所示，由图5可明显观察到两个动态衍射峰。对图5中的每条衍射线进行分析处理，利用峰巅法确定各衍射峰的位置，得到两个动态衍射峰相对于静态衍射峰的位移Δxmeasure_1和Δxmeasure_2(表1)。

a——衍射图像；b——衍射线图4 LiF晶体的静态及冲击状态的脉冲X射线衍射结果Fig.4 Result of pulsed X-ray diffraction from LiF crystal in unshocked and shocked state

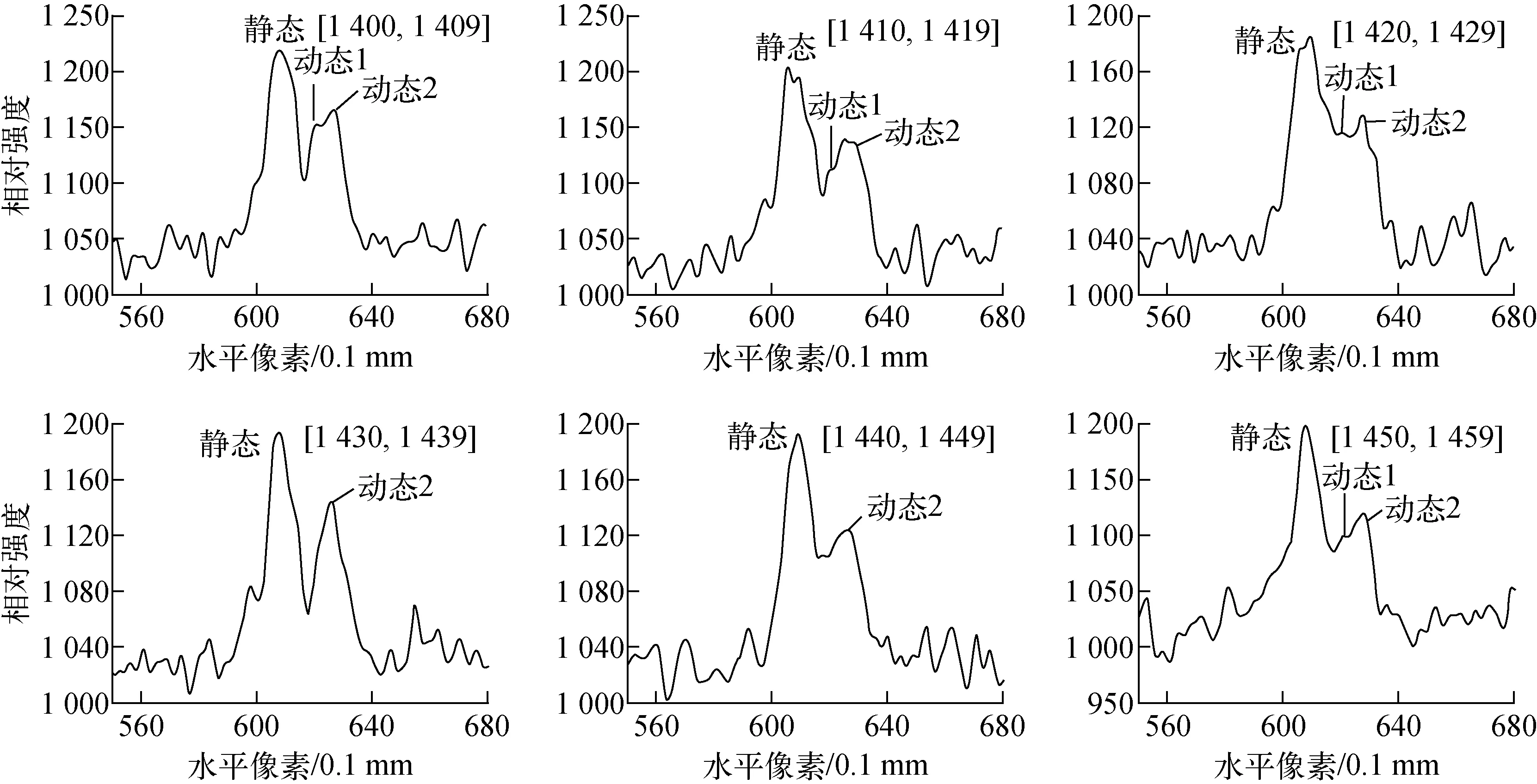
图5 不同垂直像素段LiF晶体的静态及动态衍射线Fig.5 Unshocked and shocked diffraction data of LiF crystal from different vertical pixels

表1 冲击加载下LiF晶体的衍射峰位移结果Table 1 Diffraction peak shift of LiF crystal under shock compression

根据表1可知，两个动态衍射峰的偏移量分别为：

Δxmeasure_1=1.225 mm±0.050 mm

Δxmeasure_2=1.817 mm±0.041 mm

(14)

依据式(5)～(7)，扣除撞击倾斜及晶体宏观位移造成的衍射偏移量后，得到晶格形变造成的峰偏移量为：

Δxdef1=1.128 mm±0.052 mm

Δxdef2=1.720 mm±0.043 mm

(15)

相应的衍射角变化量及晶格形变率为：

Δθ1=0.122°±0.006°

Δθ2=0.187°±0.005°

(Δd/d0)1=1.18%±0.06%

(Δd/d0)2=1.79%±0.06%

(16)

以下对实验获得的两个动态衍射峰进行分析。考虑X射线脉冲曝光时LiF晶体中不同的应力剖面状态与实验测得衍射峰的对应关系如图6所示，其中，A点表示X射线在晶体中的穿透深度。图6a中，LiF晶体中的初始冲击波未到达A点，对应右图晶体静态条件下的衍射峰即θ0处的衍射峰；图6b中，初始冲击波越过A点，对应右图中θ0处的衍射峰来自于未压缩区域晶体，θ1处的衍射峰来自于晶体中的压缩区域(A点)，对应压力为Pin；图6c中，冲击波到达LiF/VC交界面，此时晶体完全处在压力Pin的压缩状态，则θ1处的衍射峰增强，θ0处的衍射峰消失，同时稀疏波被反射并开始向晶体内传播；图6d中，稀疏波阵面与LiF/VC交界面之间的晶体所处的压力状态为Pref，此时右图中对应在衍射谱θ2处出现衍射峰，而稀疏波未到达的剩余部分晶体所处的压力状态仍为Pin，对应衍射谱θ1处的衍射峰。

根据上述分析，图4a中的动态衍射图像是LiF样品处于图6d中所对应的状态时产生的。为了验证该结论，将利用动态和静态衍射线计算得到的晶格形变率与利用LiF(100)的雨贡纽关系计算出的晶格形变率进行对比。立方结构晶体在压缩状态下晶格会出现两种不同的晶格形变状态，即各向同性压缩和单轴压缩，如图7所示。两种晶格形变状态对应的晶格形变率Δd/d0与宏观体积(或密度)压缩率μ的关系分别为：

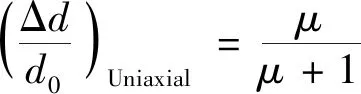
(17)

式中，μ=V0/V-1，V0和V分别为晶体静态和冲击压缩状态下的宏观体积。

表2列出了Pin和Pref压力状态下晶格形变率的计算结果和脉冲X射线衍射实验测量结果，可看出，实验测得的晶格形变率与各向同性情况吻合较好，证实了图5中的两个动态衍射峰来自于晶体的两个冲击形变状态，同时也证明了LiF(100)在冲击塑性形变下晶格为各向同性压缩(LiF(100)的雨贡纽弹性极限为0.1～0.2 GPa)。

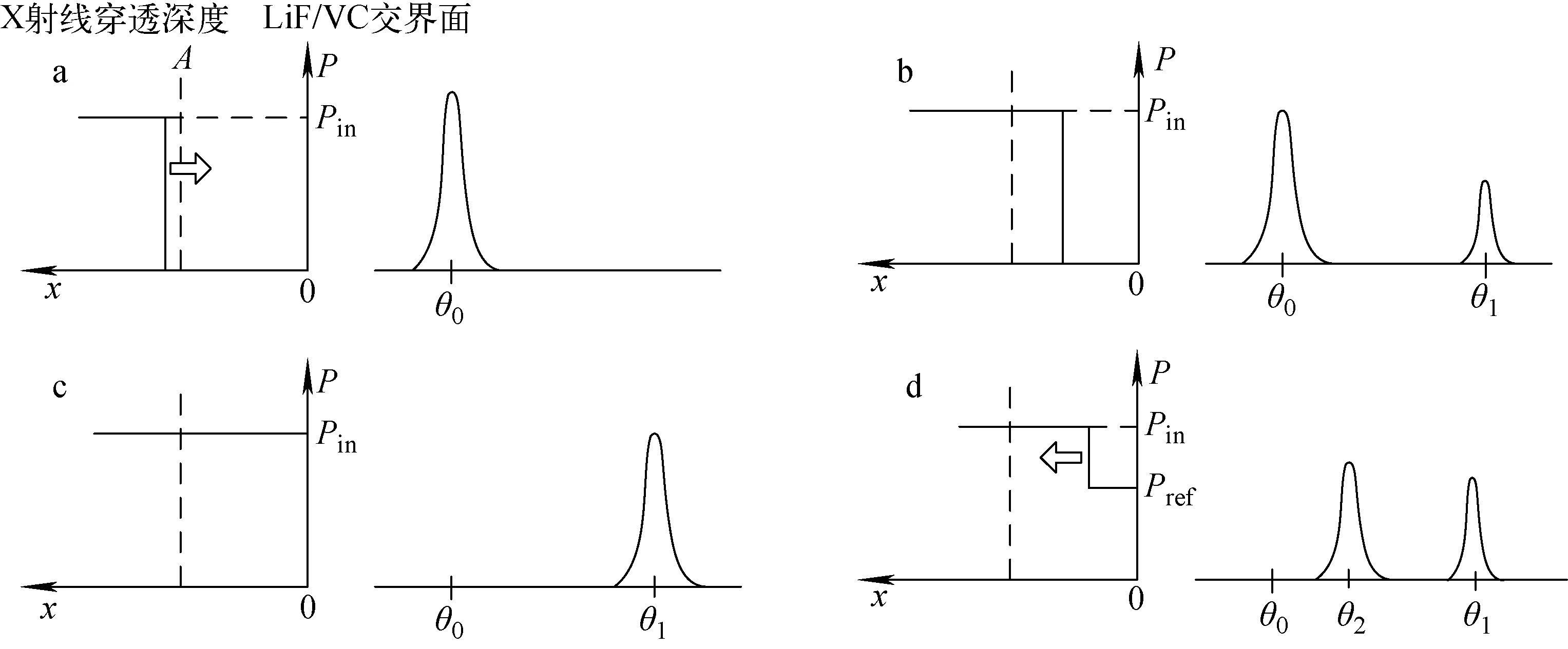
图6 X射线曝光时晶体内压力剖面与相应的衍射峰Fig.6 Sress profile in crystal during X-ray exposure and corresponding diffraction data

a——单轴压缩；b——各向同性压缩图7 立方结构晶体的两种晶格压缩状态Fig.7 Two types of unit cell compression states

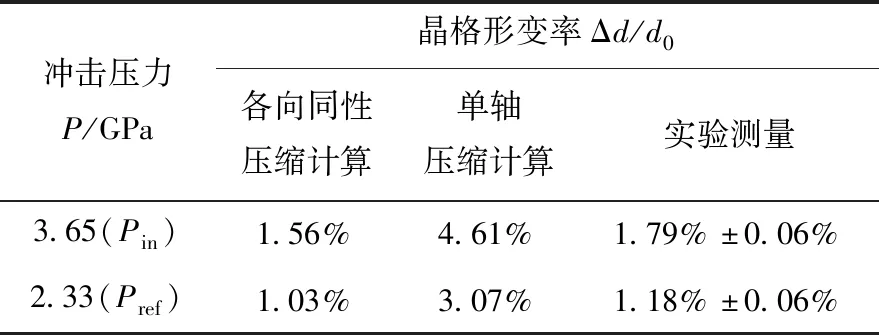
表2 实验测量结果与计算结果对比Table 2 Comparison between experiment and calculation

4 结论

本文利用脉冲X射线衍射实现了冲击加载下LiF晶体晶格形变量的定量化测量，为深入研究材料的瞬时微观动力学行为提供一种有效的诊断方法。通过提取分析沿[100]晶向加载下LiF单晶的静态和动态衍射信号特征信息，得到了不同冲击压缩状态下LiF晶体的晶格形变率，实验测量结果与雨贡纽关系计算得到的结果相吻合。本文证实了沿[100]晶向加载，当冲击加载压力超过LiF(100)的雨贡纽弹性极限，即发生冲击塑性形变时，晶格处于各向同性的压缩状态。