基于腔式探头的束团到达时间测量算法优化
2022-10-29周逸媚冷用斌曹珊珊许兴懿赖龙伟
周逸媚,冷用斌,2,*,陈 健,曹珊珊,许兴懿,2,赖龙伟
(1.中国科学院 上海高等研究院,上海 201204;2.中国科学院 上海应用物理研究所,上海 201800)
SHINE是中国首台硬X射线自由电子激光装置[1-2],总长约3.1 km,于2018年4月开始动工建设。工程任务包含一能提供8 GeV高品质电子束的连续波超导直线加速器,驱动产生的X光脉冲最高重复频率可达1 MHz;此外还将建设3条波荡器线、3条光束线以及首批10个实验站,覆盖光子能量范围0.4~25 keV,为将来物理、化学、生命、材料等多学科领域提供更先进的研究手段。目前,基于腔式探头的束流诊断系统样机平台已搭载在上海软X射线自由电子激光装置(SXFEL)上,便于束流实验的进行。
超高分辨率(fs量级)的束团到达时间测量是自由电子激光装置关键的研究问题之一。精确测定电子束团的到达时间(相位),可提高波荡器中电子束和种子激光脉冲在纵向的重合度。目前国际上常用的测量方法有电光采样法[3-4]和射频谐振腔法[5-6]。本文主要关注的是谐振腔法,由于系统结构简单,便于优化调试,该方法已应用于日本SACLA[7]、美国LCLS[8]、韩国PAL-XFEL[9]等装置。上海软X自由电子激光装置(SXFEL)也已成功运用射频谐振腔法进行束团到达时间的测量,在电荷量为600 pC时分辨率达到了13 fs[10]。在高重频的上海硬X射线自由电子激光装置中,束团到达时间的测量要求更严格,现定的技术指标是希望在电荷量100 pC时分辨率好于25 fs(相位分辨率可转化为求信噪比极大值问题,因为原始信号的信噪比和电荷量呈正比,所以,在理想情况下600 pC的指标可提高到4.2 fs)。射频谐振腔法仍尝试应用于该装置,为实现更高精度的测量要求,不仅需设计新的高分辨率、高灵敏度腔式探头[11],还需优化系统前端和信号处理算法。
束流在通过腔式探头时会激励起尾场,从而耦合出携带不同束流信息的窄带信号。TM010模式下腔体输出信号与束流横向位置无关,而信号相位由束团到达时间完全决定,因此该模式可用于束团到达时间的精确测量。典型的束团到达时间监测系统主要由腔式探头、射频前端、本振时钟模块和数字采集系统组成。在系统参数确定的情况下,要提高束团到达时间测量精度,需进行信号处理算法的优化和分析。理论上,当ADC采样率和有效位足够高时,采样信号全波形来进行相位提取可获得最佳分辨率。但在实际测量中,当腔式探头的衰减时间常数很小时,信号波形持续时间很短,信号采集的数据长度越长,相对引入的ADC噪声就越多,反而会影响系统分辨率。因此,在信号处理算法中,如何确定最佳数据处理窗口是优化系统分辨率的重要因素之一。
影响束团到达时间测量分辨率R的主要因素有腔体信号的衰减时间常数τ、系统采样率Fs、系统信噪比SNR、系统模拟带宽和信号处理时间窗口SW。本文的主要目的之一是分析系统分辨率与上述所有参数之间的依赖关系,并总结出经验公式,可用来指导完成系统最优化设计;另一个目的是判断在何种信号处理时间窗口下可获得最佳分辨率,并分析此最佳信号处理时间窗口与其他几个参数的关联性。本文将根据理论分析通过数学公式推导出相关经验公式,再利用蒙特卡罗数值仿真的方法进行分析,最后在SHINE束团到达时间监测系统样机上进行束流实验验证。
1 基本原理
1.1 CBPM探头信号分析
当带电粒子穿过谐振腔体时,会产生窄带(高信噪比)尾场信号,从而激励起电磁场的各特征模,不同模式的尾场信号携带不同的束流信息,通过不同信号处理方法可提取源束团的幅度和相位信息。此外,由于热损耗的存在,腔内电磁场振荡幅度不会一直增强,在一定时间内两者会达到平衡,从而使腔内能量保持稳定。根据麦克斯韦方程求解,谐振腔内多个谐振角频率对应不同的本征模式,而每种本征模式具有特定的频率和特定场模式,不同权重的叠加构成了腔内电磁场分布。对于标准圆柱形腔体而言,只有横向磁场(transverse magnetic, TM)模式被有效激发,振幅由损失的能量决定。通常情况下,利用TM010和TM110两种模式进行束流诊断和测量,它们的电场表达式[12-13]如下所示:
(1)
式中:E0为电场强度;J1和J0分别为一阶和零阶贝塞尔函数;u11和u01为它们的第1个根(u11=3.832,u01=2.405);r为腔体半径;ρ为径向坐标;φ为TM010模与轴向之间的夹角;ω010和ω110分别为TM010和TM110模式的腔体谐振角频率。TM110模式具有轴向反对称性,轴心两侧的电场相反(相位180°),而TM010模式的电场是中心对称的,两侧相位一致。
在束流诊断应用中,TM110模式常用作位置腔来测量束团横向位置,由于该模式下信号幅度与束团偏离中心位移呈正比,相位信息可判定束团横向偏移的方向。而本文主要关注的是TM010模式,该模式下信号幅度与束团横向位置无关,只与束团电荷量有关,因此常用作参考腔来测量束团电荷量。同时该模式下信号的相位信息可用于束团到达时间的精确测量。
根据能量守恒定律,带电粒子损失的能量部分因阻抗转化为热能,而另一部分通过耦合结构输出。谐振腔输出信号波形为一随时间t呈指数衰减的正弦振荡信号,表达式可写成:
(2)
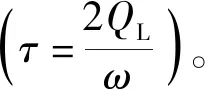
1.2 束团到达时间测量原理和方法
腔式探头信号输出的是射频(radio frequency, RF)信号,直接采样对数字采集系统的ADC要求很高,因此通常采用中频测量方案。将射频信号先下变频到中频(intermediate frequency, IF)信号再由ADC采样,这样可降低系统成本。图1为典型束团到达时间测量系统框图,谐振腔信号经同轴电缆引出,连接至射频前端模块的RF输入端;主振荡器信号经过本振时钟模块进行倍频和分频后,连接至射频前端模块的本振(local oscillator, LO)输入端;两信号在射频前端中完成混频、滤波、放大等处理,最后由IF端口输出至ADC进行锁相同步采样。

图1 典型束团到达时间监测系统框图Fig.1 Block diagram of typical bunch arrival time monitor
经混频输出的中频信号可用下式表示:
(3)
式中:中频信号幅值AIF与束团电荷量q呈正比;中频信号频率为腔体信号频率与本振信号频率之差,即ωIF=ω-ωLO;中频信号相位为两者相位差,即φIF=φ0-φLO,因此,该参数可直接用作束团到达时间测量。
1.3 最优化信号处理算法分析
针对束团到达时间测量,利用数字正交(in-phase/quadrature, I/Q)解调方式处理,信号波形如图2所示。原始谐振腔信号为图中蓝色虚线,表现为指数衰减的正弦振荡信号,单个采样点的信噪比随时间的推移而逐渐变差。当初始相位为零,本振信号频率设定为与腔体信号频率相等(零中频输出,ωIF=0)时,I信号可获得最大值,采样点信噪比最佳,波形表现为图中黄实线,式(4)可直接写成:
(4)
式中,Δφ为测量相位的误差值,是一极小量,也是评估束团到达时间分辨率的重要物理量。此时,Q信号是恒为零的一直线。而在非零中频输出时,I、Q信号表现为图中紫色正方形和绿色倒三角形振荡信号,在实际采样中各点信噪比不同,且靠近零附近的采样点信噪比极差。
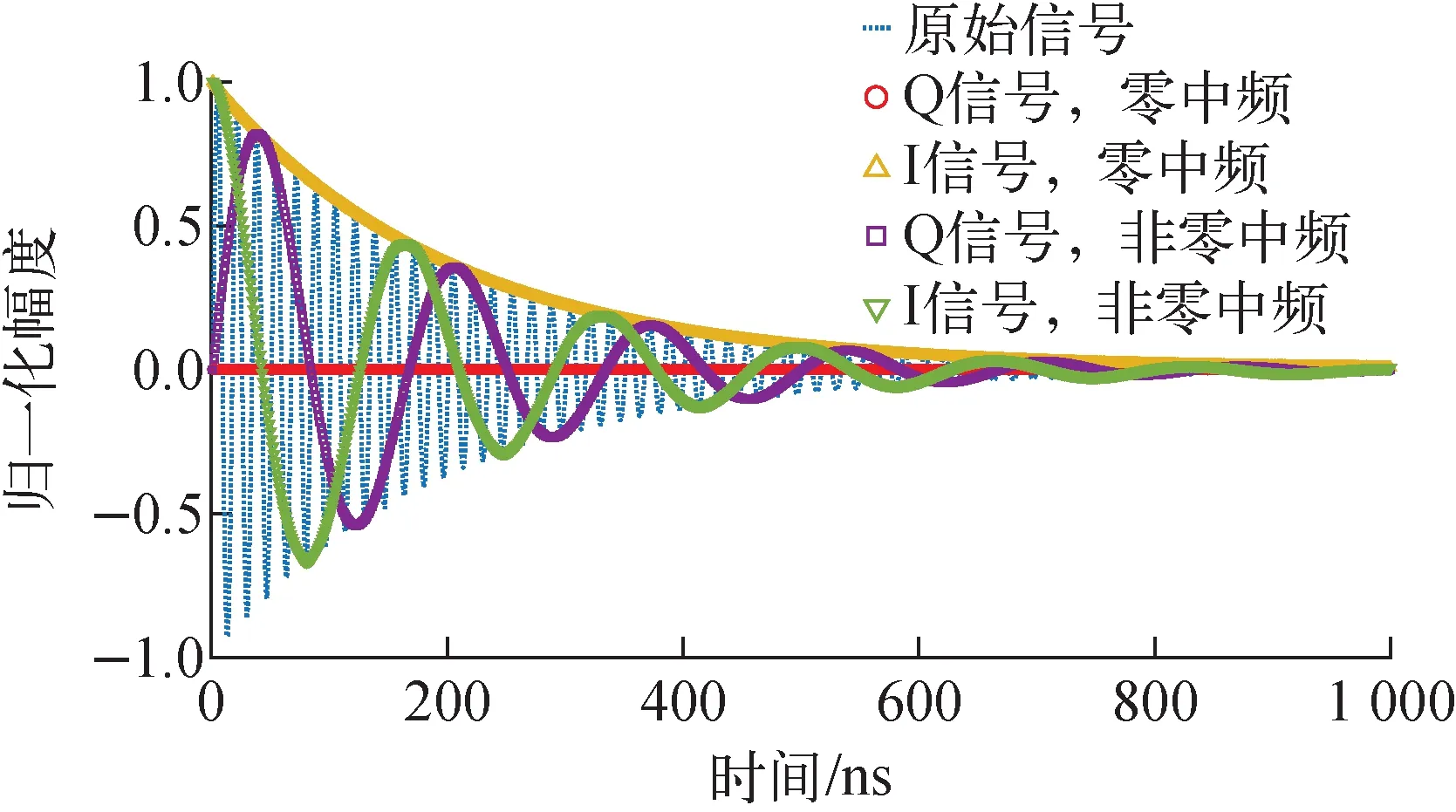
图2 最优化信号处理示意图Fig.2 Schematic diagram of optimized signal processing
在零中频输出时,相位测量问题可转化为幅度测量问题[14],存在一最佳数据处理窗口T,使得信号处理算法最优化。当ADC采样率和有效位足够高时,信号I(t)可用[0,T]区间的积分表示:
(5)
测量系统随机误差n(t)也可用积分表示:
(6)
式中:n(t)为单点采样的随机误差;σ为噪声和信号的比值,即噪信比,σ=1/SNR。
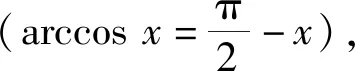
(7)
最优化信号处理算法的问题又可转化为求信噪比极大值问题,将式(5)、(6)代入式(7)后求导:
(8)
式(8)化简可得:
(9)
最终计算结果为T=1.257τ,相位提取的最佳数据窗口满足衰减时间常数的1.257倍,该结果与幅度提取窗口一致[14]。
2 信号仿真
从系统最优化的角度考虑,应选择零中频输出。原因是零中频时,原始输出信号信噪比最高,可获得系统性能最佳,且零中频推导形式简单,因此,在理论分析中选用零中频。但在实际系统搭建中,由于直流偏置、地线等影响,很难做到零中频输出。本文主要侧重的是信号处理方法中最佳数据处理窗口的研究,非零中频虽无法达到系统最佳性能,但就处理增益最大化而言,是否为零中频并不直接影响最佳数据处理窗口的选择,因此本文在仿真和实验中采用非零中频进行分析。影响束团到达时间测量系统分辨率的相关参数有原始信号的衰减时间常数、系统采样率、系统信噪比、系统模拟带宽,以及数据处理窗口等,本文将利用蒙特卡罗方法仿真这些参数的变化对系统分辨率的影响,从而总结出经验公式。同时也将利用仿真分析最佳数据处理窗口与这些参数的关系。
信号处理流程的仿真主要分为几个部分:原始信号构建(源信号+采样信号)、采样信号处理(谐波分析法)、最佳数据处理窗口相关参数仿真、最佳系统分辨率与相关参数仿真和经验公式总结。
2.1 原始信号构建
在信号仿真过程中,原始信号的构建是研究基础,需依据腔式探头工作原理,用公式及正确的信号处理流程来生成信号,并与实际采样束流信号比对,验证其可用性。首先,根据SHINE腔式探头和束团到达时间测量系统前端的设计参数[15],确定源信号的基本参数(表1),以较高采样率(20 GHz)构造源信号(幅度归一化至1),设定数据处理窗口为1 μs,如图3a所示。再根据射频前端混频工作原理,以ADC采样率(1 GHz),插值软件重采样的方式构造理想采样信号(幅度归一化至1),如图3b所示。
完成原始信号的构建后,就需提取腔式信号的相位信息,采用的主要方式是谐波分析法,截取一定窗口数据做傅里叶变换,找到信号频谱的峰值点位置,利用MatLab软件自带的求相位角函数提取峰值点对应的相位,即表征束团到达时间。图4a为叠加0.05%噪声后采样信号的频谱图,通过多样本计算标准差可评估相位测量不确定性,图4b为测量10 000次的结果,根据仿真结果可知,数据窗口为1 μs时,该系统参数下理论可得到的相位不确定性为1.9 fs。

表1 源信号基本参数Table 1 Basic parameter of source signal
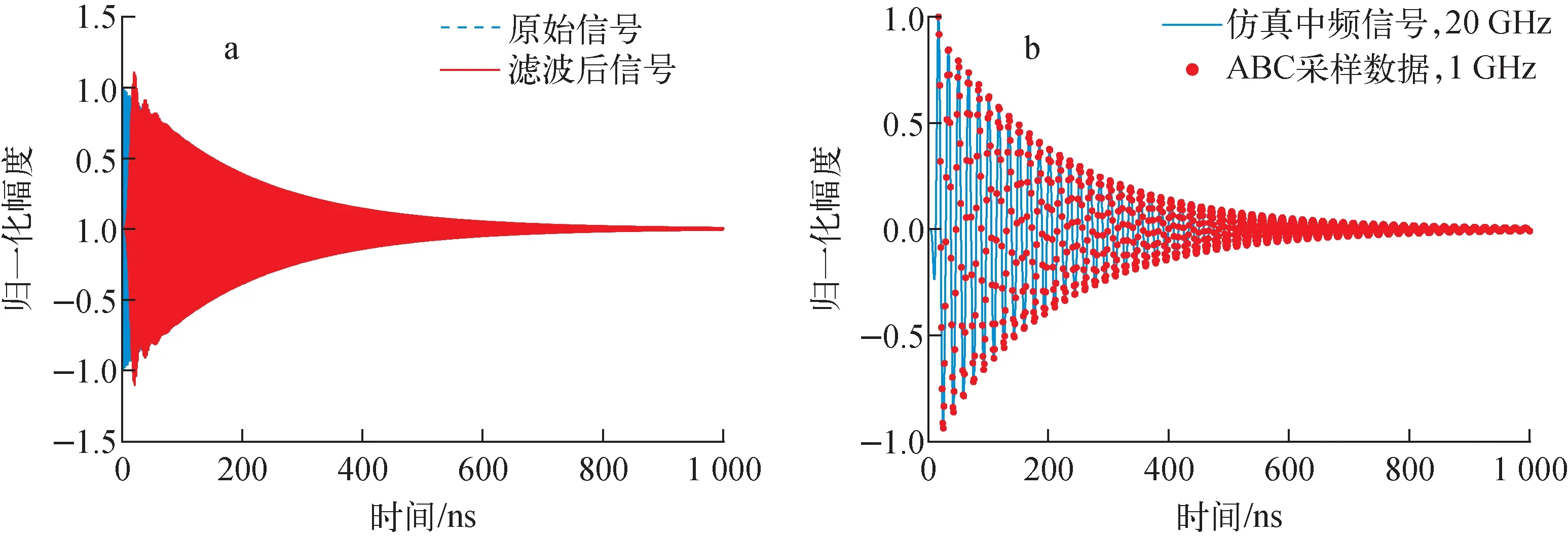
a——源信号构建;b——采样信号构建图3 源信号及采样信号构建Fig.3 Source signal and sampling signal construction
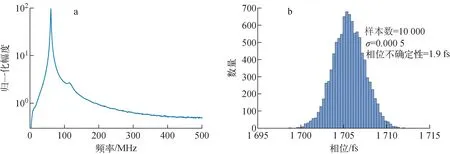
a——采样信号频谱图;b——相位不确定性图4 信号处理方法及相位不确定性评估Fig.4 Signal processing method and phase measurement uncertainty evaluation
2.2 最佳数据处理窗口相关参数仿真
根据1.3节的理论分析,影响最佳数据窗口的参数仅衰减时间常数,而与系统采样率、系统信噪比、系统模拟带宽均无关。利用数值仿真的方式对各参数进行验证。
2.2.1衰减时间常数 图5为仿真的不同数据处理窗口下的束团到达时间不确定性。从图5可看出,在数据处理过程中,在一定范围的衰减时间常数下存在一最佳处理窗口,使得相位测量不确定性最小。随着衰减时间常数的增大,最佳数据处理窗口也变大,两者呈线性关系,如图6所示,通过拟合可知其仿真结果符合理论分析。
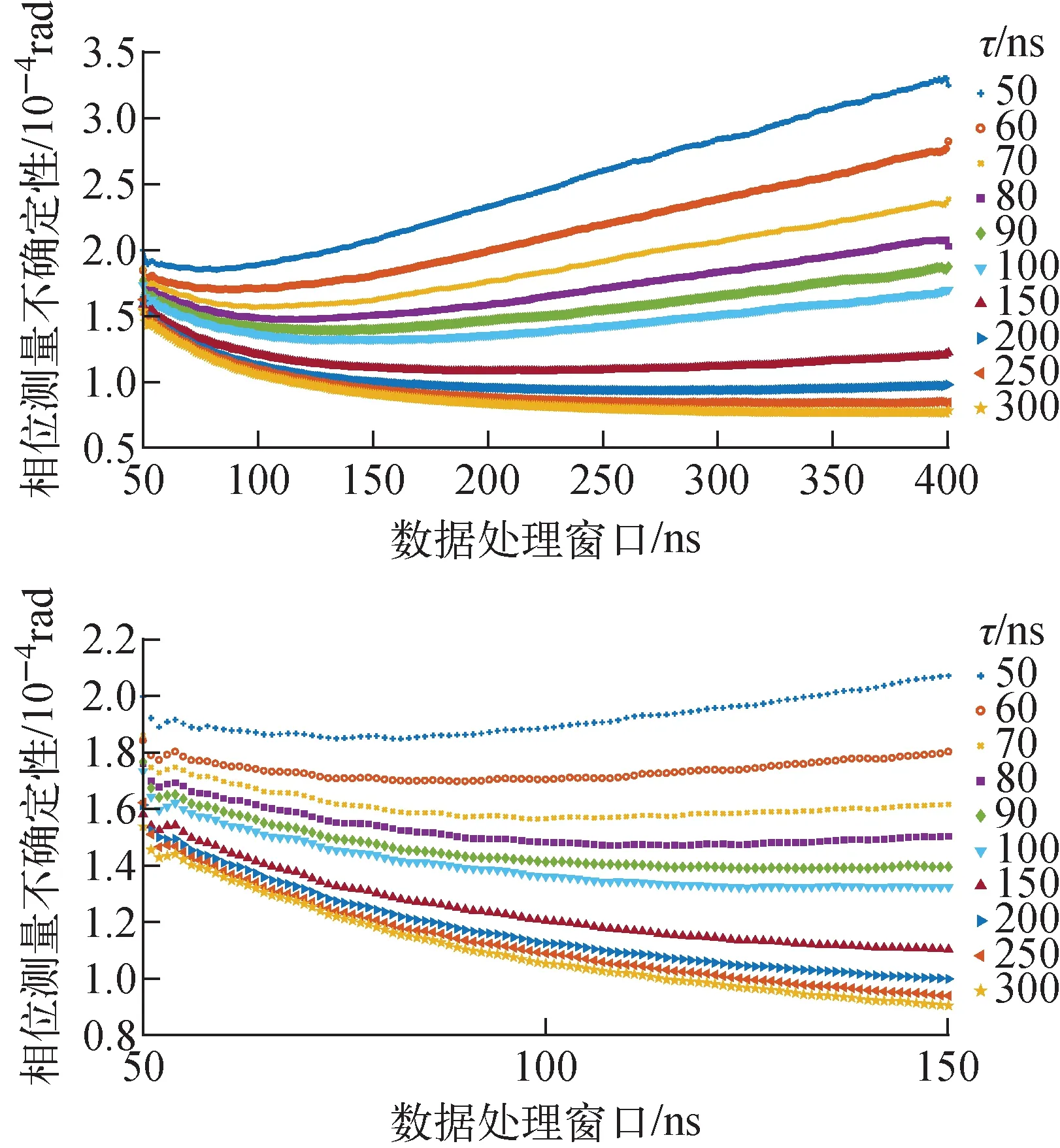
图5 不同数据处理窗口下的束团到达时间不确定性Fig.5 Uncertainty of bunch arrival time under different data processing windows

图6 最佳数据处理窗口与衰减时间常数的关系Fig.6 Relationship between optimal data processing window and decay time
2.2.2其他参数 图7~9分别仿真了不同衰减时间常数下最佳数据处理窗口与系统信噪比、系统采样率和系统带宽的关系,从图可知,最佳数据处理窗口与这些参数无关,验证了1.3节的理论分析。
2.3 相位测量不确定性相关参数仿真


图7 不同信噪比下的最佳数据处理窗口Fig.7 Optimal data processing window under different single-noise ratios

图8 不同采样率下的最佳数据处理窗口Fig.8 Optimal data processing window under different sampling rates

图9 不同带宽下的最佳数据处理窗口Fig.9 Optimal data processing window under different bandwidths
2.3.2最佳系统分辨率经验公式 根据上述各参数的数值仿真,总结归纳最佳相位测量不确定性的经验公式:
(10)
对多参数进行综合仿真,结果如图11所示,从图中可看出式(10)成立,且比例系数K约等于1.21。

图10 相位测量不确定性相关参数仿真Fig.10 Simulation of phase measurement uncertainty and related parameters

图11 最佳相位测量不确定性与相关参数的经验公式仿真结果Fig.11 Simulation of empirical formulas for optimal phase measurement uncertainty and related parameters
3 初步实验验证
根据理论分析,最佳系统分辨率只与系统信噪比SNR、系统采样率Fs和衰减时间常数τ有关,因此相关束流实验可在SHINE束团到达测量系统样机上进行,一些重要参数列于表2。
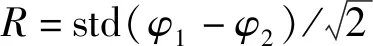

表2 SHINE束团到达测量系统样机的重要参数Table 2 Important parameter of bunch arrival measurement system in SHINE

a——QT7135采样数据;b——不同数据处理窗口;c——时间窗口1 μs时相位;d——最佳时间窗口下相位图12 SHINE样机束流实验结果Fig.12 Result of beam experiments in SHINE prototype
4 结论
基于射频谐振腔的束团到达时间测量已广泛应用于自由电子激光装置,高精度束团到达时间提取算法对于优化系统性能有重要意义。针对确定的束团到达时间监测系统,优化信号处理算法主要考虑系统采样率、系统模拟带宽、系统信噪比和数据处理长度等因素的影响。本文通过理论分析与数值仿真相结合的方式,获得束团到达时间分辨率与各参数的依赖关系。由仿真结果可知:信号处理过程中,存在一最佳数据处理时间窗口,在该窗口下可获得最佳束团到达时间测量系统分辨率。最佳数据处理时间窗口是腔体衰减时间常数的1.257倍,与系统信噪比、采样率和模拟带宽等参数均无关。同时,初步束流实验也在SHINE样机上进行验证,在系统信噪比、采样率和模拟带宽一定的情况下,最佳数据处理窗口与仿真预估值符合较好。
