液态金属高温热管传热极限研究

张嘉睿，田智星，王成龙，田文喜，郭凯伦，秋穗正，苏光辉

(西安交通大学 核科学与技术学院，陕西 西安 710049)

热管作为一种具有极高传热效率的传热元件，可以在没有外部功率输入的情况下，依靠很小的截面积远距离传输大量能量[1-2]，具有导热性高、等温性优良、结构简单、成本低廉、环境适应性强、安装维修方便等优点。将热管应用于反应堆系统可以避免单点失效，提高固有安全性[3-4]。虽然热管有着很强的传热性能，但仍受到许多因素的影响和制约，其中重要的一项为热管的传热极限，即热管在工作过程中会出现一系列传热极限来制约热管的传热[5]。热管的传热极限主要来源于两个因素[6]：蒸气流动性质和冷凝工质回流不足。这些传热极限主要包括：连续流动极限、冷却启动极限、粘性极限、音速极限、夹带极限、毛细极限、冷凝极限和沸腾极限[7]；其极限值与热管本身息息相关，如：热管的形状尺寸、吸液芯的结构与材料、热管内的工作介质、热管的工作温度等。在分析热管的传热极限时，只关心在一定工作温度下这些传热极限的最小值[8]。

连续流动极限模型是应用气体状态方程根据Knudsen数推导得出的，Faghri[9]及Tian等[10]提出了蒸气转变温度的计算方法。夹带极限的发生与Weber数(We)有关，通常采用We=1作为夹带极限的判断标准，庄骏等[11]、Chi[12]、Prenger[13]、Tien和Chung[14]、Kemme[15]、Weber-Carstanjen[16]、Kim等[17-18]均提出了不同的理论模型。由于毛细结构可能会阻碍表面波的生长，因此在毛细驱动的热管中可能不会发生夹带现象，为了验证这一点有必要进行理论与实验相结合的研究[19]。

本文针对高温钠热管展开研究，进行高温热管传热极限的理论验证与规律总结。搭建考虑不同加热功率、倾角和冷却方式等因素的高温热管传热极限测试分析实验平台，总结高温热管连续流动极限与夹带极限的发生规律，根据实验热管对两种极限的数学模型进行完善，旨为将来热管在特种装备上的应用提供实验数据与参考。

1 实验系统设计

1.1 实验装置

本实验针对工质为钠的毛细驱动高温热管开展实验研究，设计搭建了高温热管传热极限测试分析实验平台。高温热管传热极限实验平台主要包括实验热管、电源系统、加热系统、定位系统、冷却系统等。实验平台的结构、高温热管的加热系统及冷却系统布置示意图、实验平台实物图分别如图1～3所示。实验平台的电加热功率范围为1～20 kW，采用感应式加热，实验系统通过冷却管中的冷却水降温。

图1 实验平台结构Fig.1 Structure of experimental bench

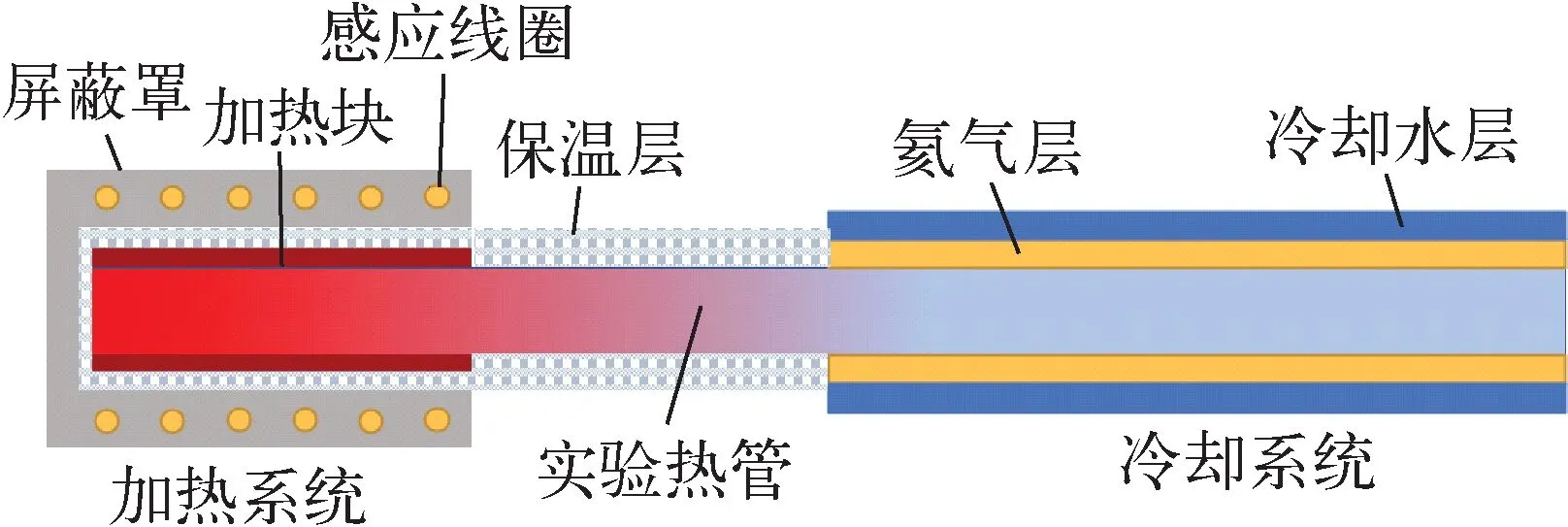
图2 高温热管的加热系统及冷却系统布置示意图Fig.2 Layout diagram of heating system and cooling system of high-temperature heat pipe

图3 实验平台实物图Fig.3 Physical image of experimental bench

实验采用高温钠热管，其长度为2 m，管壳材料为HAYNES233，工质材料选用99.7%的钠，吸液芯材料为不锈钢，目数为800，孔型为席型。在热管管壁内外均布置有K型热电偶进行温度测量，热管测点的布置如图4所示。加热系统的主要作用是提供磁场；定位系统主要功能是固定实验热管，并根据实验需要调节热管的水平倾角。冷却系统为实验装置提供必要冷却，热管的传热功率通过冷凝段水套的冷却功率获得，冷却水套进出口设置有K型热电偶和压力表，冷却水流量可由流量计获得，传热功率可由式(1)获得。

(1)

1.2 实验方法与工况设计

本实验通过测量热管功率和管壁温度分布来分析热管稳态及瞬态特性。通过调节不同的倾斜角度(蒸发段朝上与水平面形成的正角度)和施加不同的加热功率，对热管传热极限进行实验研究。

图4 热管测点位置Fig.4 Position of measurement point for heat pipe

对不同工况下液态金属高温热管传热极限的发生现象及规律进行分析。在通水强制对流冷却的条件下，设计的电源加热功率范围为1～7 kW，水平倾角范围为0°～90°。具体实验工况列于表1。

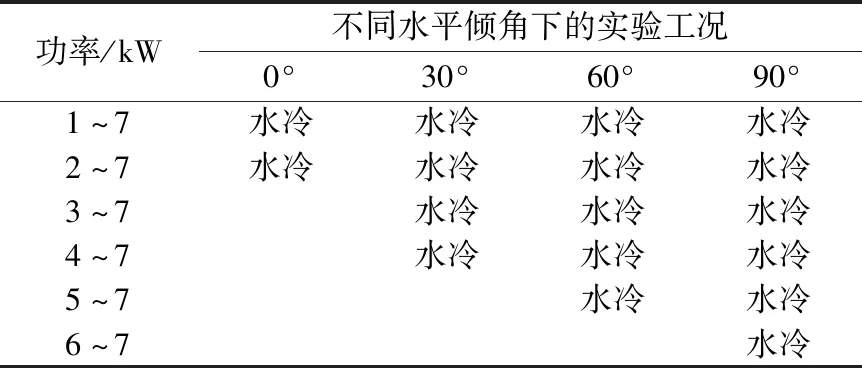
表1 高温热管传热极限实验工况Table 1 Heat transfer limitation experimental condition of high-temperature heat pipe

1.3 不确定度分析

本实验采用K型铠装热电偶来测量高温钠热管管壁、蒸气腔及进出口水温的温度，热电偶的仪器误差为3 ℃。热电偶测点温度的不确定度为：

(2)

式中：uB为温度B类评价的不确定度，℃；Δ仪为热电偶仪器误差，℃；k为误差均匀分布的置信区间，k=31/2。

冷却功率的不确定性分析：水冷功率可由式(1)求得，过程中流量计的精度为0.5%；冷却水的进出口焓的精度采用温度测量的精度，即式(3)。根据以上分析，得出冷却功率的不确定度为0.6%，见式(4)。

(3)

(4)

式中：Q为传热功率，W；T为温度，℃。

2 热管传热极限结果与分析

2.1 连续流动极限实验结果

图5示出了热管在不同水平倾角下的启动过程。连续流动极限的衡量标准是蒸气转变温度，蒸气温度高于转变温度后，热管内蒸气工质由自由分子转变为连续流动状态，热管启动。由图5可见，蒸气曲线中温度上升阶段存在1个拐点，拐点之后蒸发段蒸气温度趋于一致，说明工质由自由分子状态变为连续流动状态，拐点之前传热能力受限，即该拐点代表连续流动极限的转变温度。可得出以下结论：热管连续流动极限的发生影响热管的启动；由于水平夹角较大时转变温度较大，因此大角度下的热管更容易发生连续流动极限。

2.2 夹带极限实验结果

由于热管工作时存在两相逆流，当蒸气流流速较大时，作用于气-液相界面处的力将变大，回流的液体就有可能被蒸气流夹带至冷凝段，导致蒸发段缺液干涸。实验得到夹带极限的图像如图6所示。

图中的数字标注代表了热电偶测点距离热管蒸发段顶端的长度图5 充液量158 g热管在不同水平倾角下的启动过程Fig.5 Starting process of 158 g liquid filled heat pipe under different horizontal inclinations

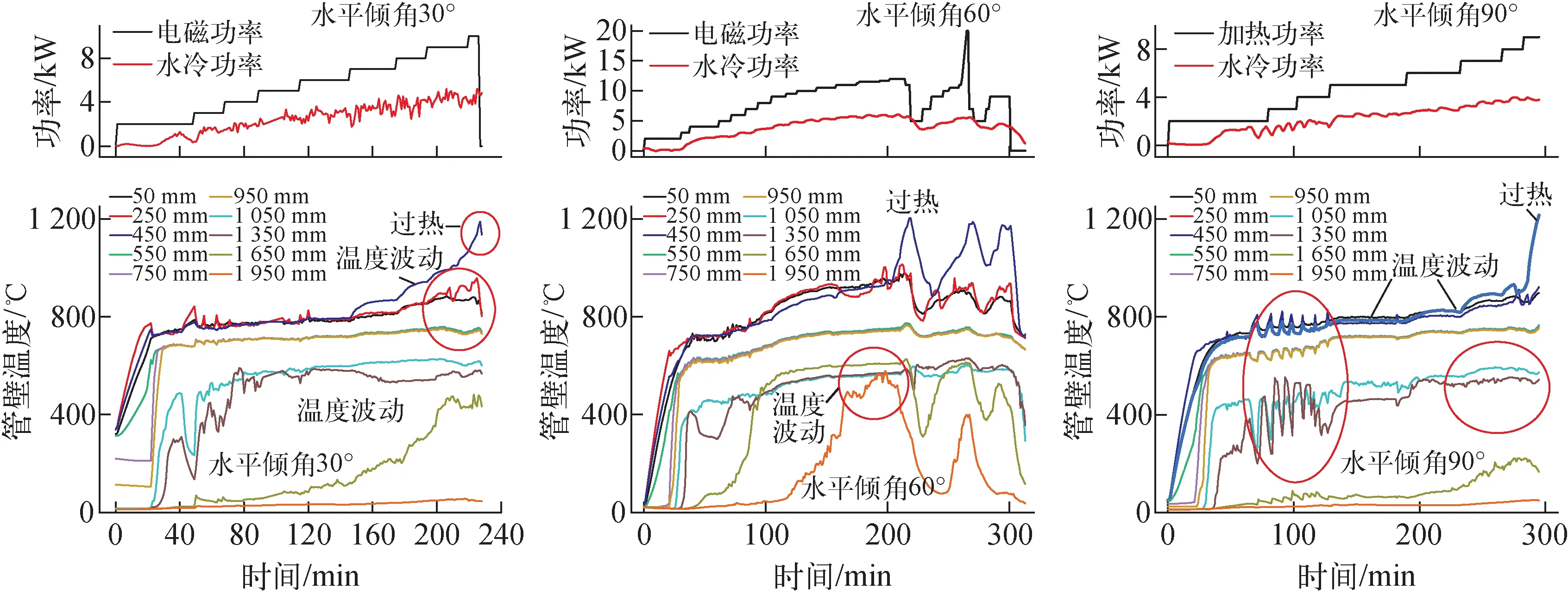
图6 充液量208 g热管实验得到夹带极限的图像Fig.6 Image of entrainment limit was obtained by 208 g liquid filled heat pipe experiment

当水平倾角为0°时，重力作用与吸液芯的毛细力作用使得回流工质大部分在吸液芯内流动，液膜不容易被蒸气流撕裂，液体也就不容易被夹带至冷凝段。当水平倾角为30°、60°和90°时，重力在热管轴向存在一个分力使得回流液体的回流能力增强，同时重力在热管径向的分力减小，由于毛细力是垂直于气液界面的力，恰好与重力在径向的分力方向相反，因此液体流至吸液芯中的力减小，导致一部分冷凝液体将不在吸液芯内回流，而是在吸液芯表面流动。这增大了液体与蒸气流的接触面积，使液膜容易被撕破，造成这部分回流液体被夹带至冷凝段，最终导致了蒸发段工质的干涸，出现过热。同时被夹带到冷凝段的液体由于温度较低，在冷凝段吸热导致冷凝段出现温度波动，热管达到夹带极限。

可以得出以下结论：热管的夹带极限与热管水平倾角的大小有着较大关联，当热管水平倾角较小时，热管不容易出现夹带极限，但却由于回流能力不足而可能导致毛细极限。因此在实际应用时，需要考虑水平倾角的两面性，选择最佳的热管运行水平倾角。

2.3 理论模型分析

1) 连续流动极限

研究中，连续流动极限理论模型的得出是利用Knudsen数进行推导，不同蒸气工质所得出的最终数学模型不同，针对以钠为工质的高温热管进行转变温度的推导：

(5)

(6)

(7)

式中：T为蒸气温度，℃；D为热管蒸气腔直径，m；σ为碰撞直径，m；k为玻尔兹曼常数；Kn为Knudsen数。利用式(6)与式(7)进行迭代计算，得到实验热管的转变温度515.795 ℃。原有理论计算得出的转变温度与实验所测得的转变温度对比如图7所示。与实验所得的转变温度作比较可以发现结果较为接近，且小角度工况下较为适用，误差在6.58%以内；而大角度下则不适用，误差超过28%。

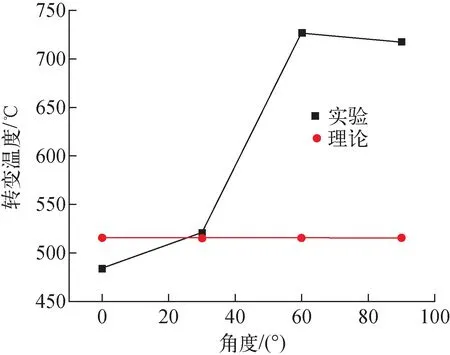
图7 理论计算得出与实验测得的转变温度对比Fig.7 Comparison of transition temperatures calculated by theory and measured by experiment

2) 夹带极限

判断液滴夹带的发生与否可以根据We的大小，其定义为蒸气流动惯性力与吸液芯液体表面张力之比。在计算夹带极限时，视We=1，考虑波诱导夹带[17]，由Wallis相关系数[20]和泰勒不稳定性的临界波长推导得到式(8)，以此进行功率的计算。

(8)

式中：Qent为夹带极限功率，kW；ρv为蒸气密度，kg/m3；ρl为液体密度，kg/m3；Av为蒸气腔横截面积，m2；σ为工质液体表面张力，N/m；hfg为工质汽化潜热，J/kg；CW与Ct为无量纲数，CW取1.0，Ct取2π×3-0.5。

对倾角为30°、60°、90°的工况进行理论计算，得到实验功率与理论功率的对比列于表2。可看出，平均实验功率与平均理论功率在不同角度均存在误差，且在大角度工况下误差较大，90°工况下误差大于100%，并不适用。对此，本文提出一种修正方法，将在2.4节中详细讨论。

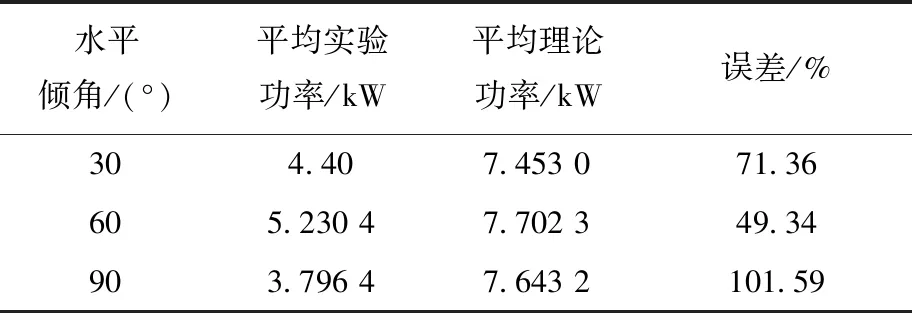
表2 不同水平倾角夹带极限实验功率与理论功率对比Table 2 Comparison of experimental and theoretical powers of entrainment limitation at different horizontal inclinations

2.4 模型修正

1) 连续流动极限

连续流动极限的数学模型仅为理论推导，在假设理想气体的条件下得出了一个转变温度的迭代公式，对于某根给定热管，当确定热管管径与蒸气腔直径时，由理论模型得出的连续流动转变温度为一个确定的值。而在本文数据分析中可发现，当热管处于不同倾斜角度时转变温度是不同的，且当水平倾角较大时，热管的转变温度较大。因此，本节仅针对实验热管，对于高温热管连续流动极限在考虑水平倾角影响下进行理论模型的完善。

拟建立一个实际转变温度T′tr与理论转变温度Ttr关于角度θ的函数T′tr=Ttrf(θ)，采用本实验的结果针对热管连续流动极限的数学模型进行完善，加入重力影响因素，具体拟合结果如图8所示。

由拟合结果可得出，实验热管的连续流动极限数学模型为：

T=

(9)

图8 连续流动极限拟合结果Fig.8 Continuum flow limitation fitting result

2) 夹带极限

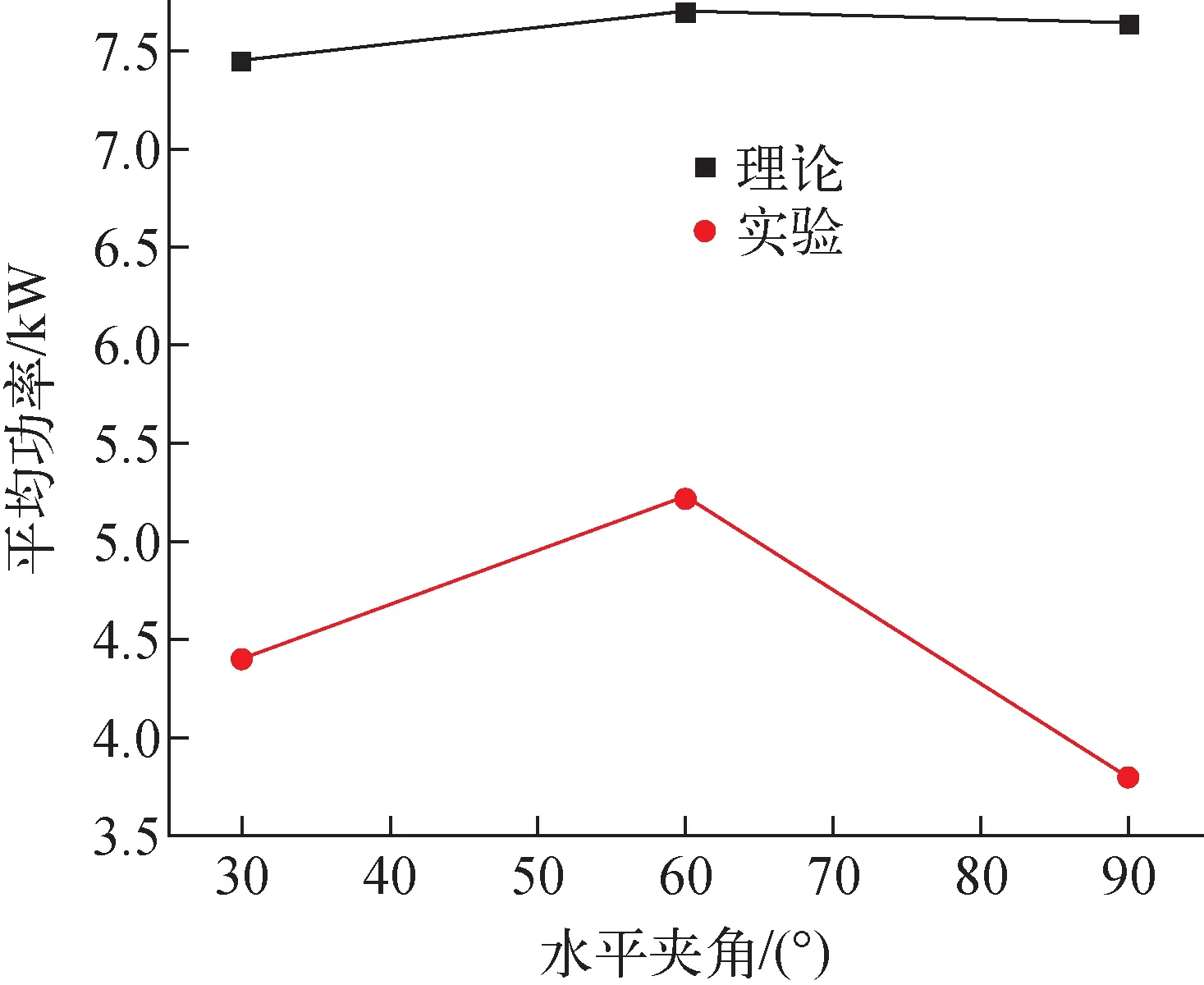
图9 理论计算与实验测得的功率对比Fig.9 Comparison of theoretically calculated power and experimentally measured power

图9为理论计算与实验测得的功率对比，可得出，理论模型计算结果与实验结果相差较大，说明理论模型中并未考虑热管角度的影响。因此拟建立一个实际功率与理论功率关于角度的函数，针对本实验热管，对于夹带极限在重力因素影响下进行数学模型的完善。由于实验中仅进行了0°、30°、60°与90°的工况，在30°、60°与90°的工况下发生了夹带极限，因此在考虑水平夹角的影响时仅能使用3个点进行拟合，结果较为粗略，因此也将进行蒸气温度的拟合，考虑温度修正。

对于角度修正，由于实验仅有3个点，因此在拟合过程中，可得到1条经过3点的精确曲线，在实验热管水平倾角处于30°～90°时，可应用该拟合进行夹带极限的功率计算。取各角度下发生夹带极限的部分功率，红点为各角度下功率的平均值，结果是对平均值进行的拟合；对于温度拟合，取发生夹带极限的部分温度进行拟合。图10所示为夹带极限的拟合结果。

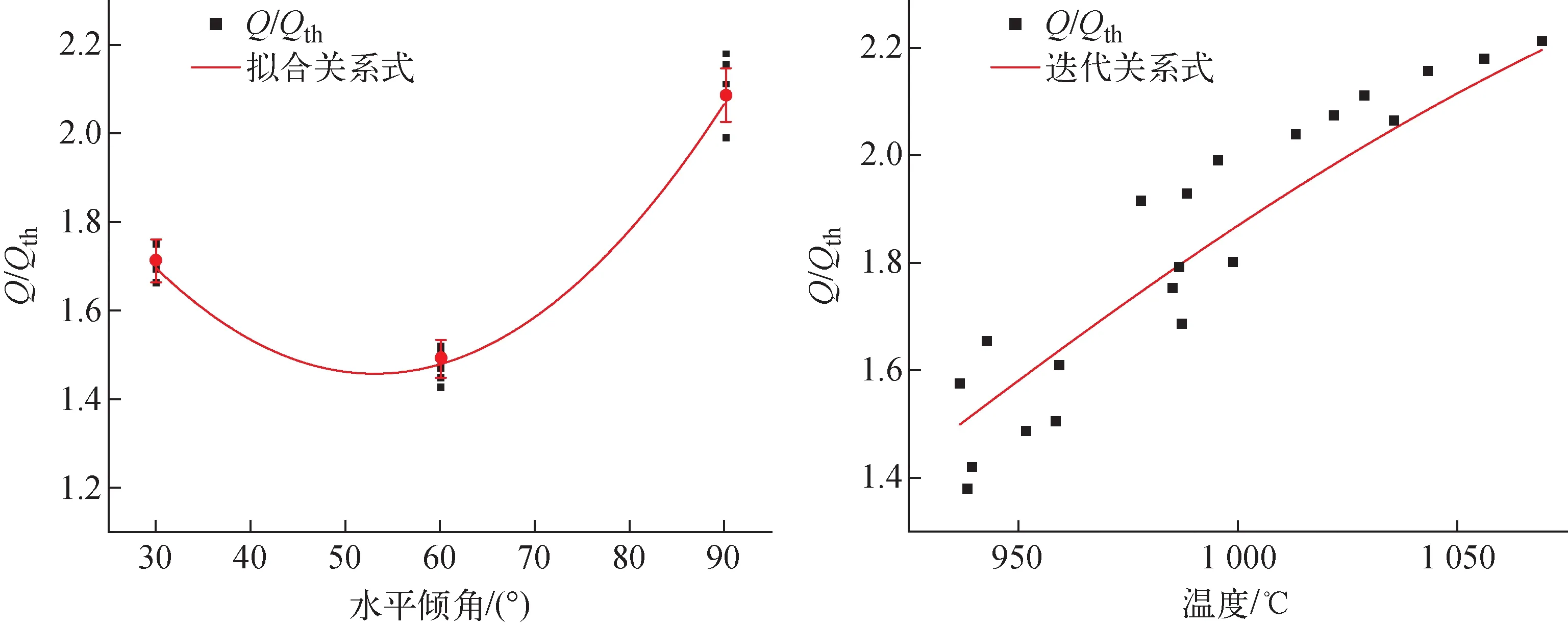
图10 夹带极限拟合结果Fig.10 Entrainment limitation fitting result

结合现有的夹带极限的数学模型，可得出实验热管在不同水平倾角下夹带极限的数学模型：

(10)

式中：Qe,max为修正后的热管夹带极限功率，kW；A=2.750，B=0.004 7，C=4.475×10-4，D=2.750±1.230，E=-0.009 0±0.008 4，F=916.522±84.725。

3 结论

本文设计搭建了工质为钠的高温热管分析测试实验平台，对高温热管的传热极限进行了实验研究，并在理论模型的基础上对实验进行了分析，得出了高温热管传热极限的发生规律，并与数学模型进行了对比，本文获得以下结论。

1) 热管连续流动极限的衡量标准为转变温度，在蒸气温度曲线上表现为1个拐点；大角度下的热管更容易发生连续流动极限；水平倾角对热管连续流动极限影响十分显著，60°工况下的热管转变温度较30°工况下的转变温度高200 ℃左右。连续流动极限转变温度的得出需要考虑工质的物性进行推导与迭代，原有理论计算的转变温度与实验所得的转变温度结果较为接近，且小角度工况下误差在6.58%以内，大角度下误差超过28%。

2) 热管的夹带极限与热管的水平倾角有着较大关联，实验热管在0°工况下未发生夹带极限，而在30°、60°和90°工况下均发生夹带极限。当热管水平倾角较大时容易产生夹带极限，可减小倾角避免夹带极限的发生。数学模型在不同角度工况下均存在误差，角度较大时误差较大，90°工况下误差大于100%。

3) 针对实验热管，对于连续流动极限与夹带极限将理论计算结果进行数据拟合，最终得出了适用于本实验热管的考虑了重力因素的连续流动极限的理论模型和考虑了重力因素与温度影响的夹带极限的理论模型。

本文针对高温热管进行了传热极限的实验研究，通过实验观测高温热管的毛细极限、转变温度、夹带极限、音速极限、冷凝极限与冷却启动极限，总结高温热管传热极限发生规律，为热管的性能提升和优化提供参考。