基于几何的V2V三维MIMO信道建模及统计特性分析

张 薇, 桑溪鸿, 韩 慧, 杨博文

(1. 哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001;2. 电子信息系统复杂电磁环境效应国家重点实验室, 河南 洛阳 471003)

0 引 言

随着第五代(the fifth generation,5G)无线通信网络进入商用的部署阶段,即将到来的超5G(beyond 5G, B5G)/第六代(the sixth generation,6G)无线通信网络越来越受到关注。车对车(vehicle to vehicle,V2V)通信技术通过车载终端进行车辆之间的通信,是一种不借助于固定式基站的移动通信技术,是B5G/6G通信技术在智能交通领域中的应用。多输入多输出(multiple input multiple output,MIMO)技术通过空间分集技术和空间复用技术,在发射端(transmitter,T)和接收端(receiver,R)部署多根天线,可以提高通信系统的可靠性和扩大系统的容量,在设计车载无线通信系统中广为应用。实际情况下,收发端天线的空时相关特性会严重影响V2V通信系统的性能,因此构建符合实际场景的V2V信道模型并对其特性进行研究,对V2V通信系统的设计及部署具有重要应用价值。

现有主流的V2V MIMO信道建模方法分为3种:基于几何确定性建模(geometry based deterministic modeling,GBDM)、非几何随机建模(non geometrical stochastic modeling,NGSM)和基于几何随机建模(geometry based stochastic modeling,GBSM)。GBSM具备高效性和准确性的优点,被广泛应用于V2V通信系统的设计中。根据实际散射环境不同,GBSM建立的模型可分为单环模型、双环模型、椭圆模型、圆柱模型等,在此基础上还分为二维模型和三维模型。文献[12]首次提出单环模型,假设一端移动一端静止,移动端周围的散射体均匀分布在圆环上,发射信号经一次散射(single bounced,SB)到达接收端。文献[13]首次提出双环模型,假设收发端周围都有分布在圆环上的散射体,发射信号经二次散射(double bounced,DB)到达接收端,但没有考虑周围静止的散射体对信道的影响。文献[14]建立了Von-Mises分布下椭圆散射信道模型,并仿真分析了信道空时相关特性。除了散射体的分布能对信号增益产生影响,车流量密度(vehicular traffic density,VTD)也是影响车载通信的重要因素之一。文献[16]首次引用VTD的概念并采用双环模型和椭圆模型对移动的车辆和路边静止的散射体建模,仿真分析了空间互相关函数(cross correlation function,CCF)和多普勒功率谱密度(Doppler power spectrum density,DPSD)。

上述文献仅考虑二维 GBSM,而信号实际传播过程中,散射体的高度、天线间的仰角不可忽略。二维模型的考虑过于理想化,需要建立三维模型,使V2V MIMO信道的刻画更加准确。文献[18-22]引入仰角,提出三维 MIMO V2V GBSM,并通过仿真分析天线阵列和散射环境等多种因素对信道统计特性的影响,最后验证了模型的准确性和有效性。但上述三维模型未考虑由交通堵塞导致高VTD和较空旷情况下低VTD场景对V2V信道统计特性的影响,而VTD反映的是交通状况的直观特征,可以通过改变不同分量的功率占比反映对信道的影响。文献[23]提出的三维V2V GBSM结合VTD研究了对信道空时相关特性的影响,但并未考虑VTD对信道其他统计特性的影响。

本文的主要贡献包括以下3个方面:① 在文献[19]所提模型基础上,将有效散射体的分布扩展至360°,同时考虑车流量密度的影响,提出一种新型的三维 MIMO V2V GBSM参考模型,该模型可适用于各种V2V通信场景;② 根据所提参考模型中的方位角和仰角的关系,推导了时间自相关函数(auto correlation function,ACF)、CCF、DPSD、电平通过率(envelope level crossing rate,LCR)和平均衰落持续时间(average fade duration,AFD)的表达式,研究了散射体位置、天线阵列位置对信道空时相关特性的影响;③ 重点分析不同VTD下二维模型和三维模型信道统计特性的异同。同时,本文利用合理算法进一步推导了仿真模型,并通过实测和仿真数据验证了仿真模型的效用。本文的研究扩展了V2V GBSM建模方法,提高了分析和仿真MIMO V2V系统的效率。

1 三维MIMO V2V 信道模型

1.1 参考模型

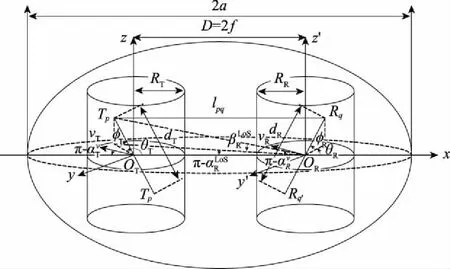
图1 3D MIMO V2V 信道模型Fig.1 3D MIMO V2V channel model

图2 包含LoS、SB和DB的几何角度和路径长度的MIMO V2V信道模型Fig.2 MIMO V2V channel model including geometric angle and path length of LoS, SB and DB

表1 模型参数及定义Table 1 Model parameters and definitions

V2V MIMO衰落信道可以表征为×的信道矩阵()=[()]×。其中,()表示T第个天线阵列到R第个天线阵列之间的时变信道冲激响应,由LoS分量、SB分量、DB分量组成,其中SB分量由围绕T圆柱体上散射体作用的SB分量、围绕R圆柱体上散射体作用的SB分量和椭球体上散射作用的SB分量组成,分别记为SB、SB和SB。因此,总的()具体表示为

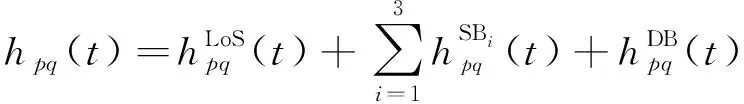
(1)

其中LoS分量表示为

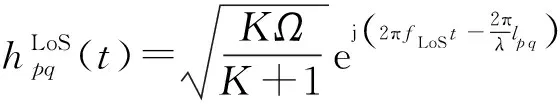
(2)

SB分量是SB、SB和SB的叠加,即:

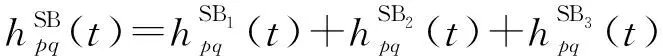
(3)

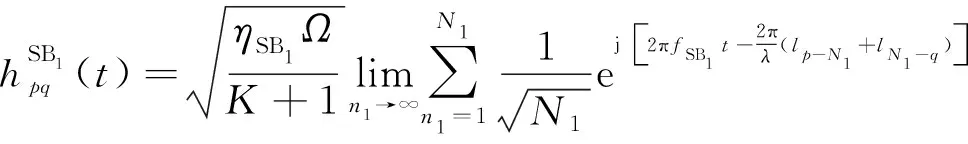
(4)

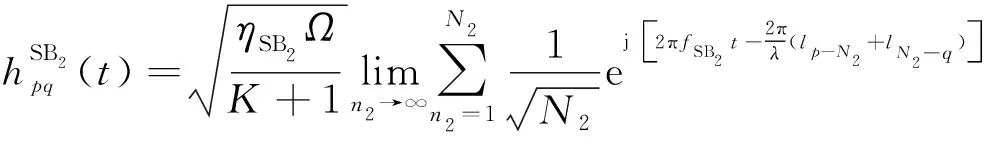
(5)

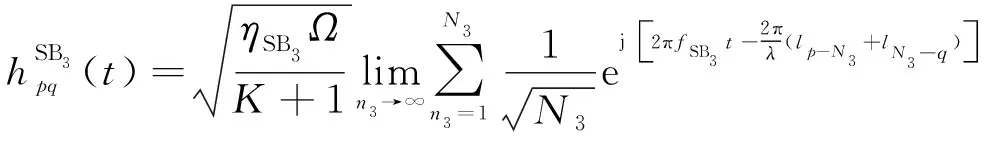
(6)

DB分量表示为

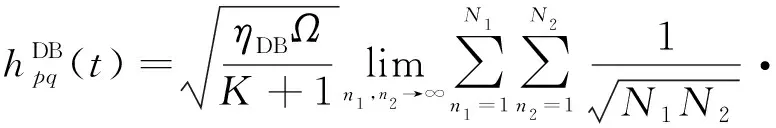
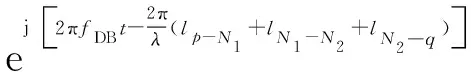
(7)

式中:为莱斯因子;为链路到链路的总功率;SB、SB、SB和是各分量的归一化功率相关系数,并且满足功率和为1;=c代表载波波长,c是光速,是载波频率;、、分别表示LoS分量、SB分量和DB分量的多普勒频移。

下面根据图2中的几何关系计算各分量的多普勒频移和路径长度。LoS分量的多普勒频移:

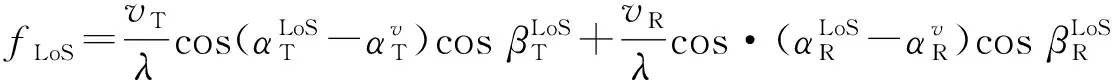
(8)

LoS分量的路径长度:

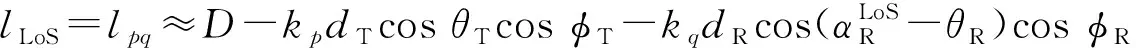
(9)

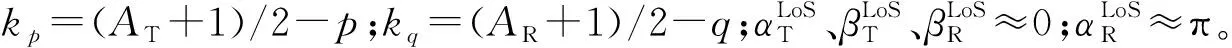
SB分量中,-,-由几何关系可表示为

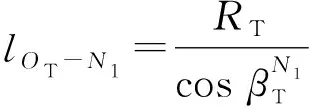
(10)

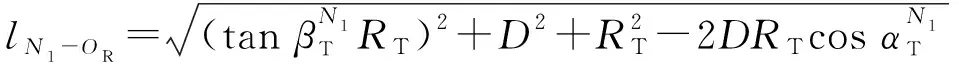
(11)

注意模型中SB分量的AAoD、AAoA、EAoD、EAoA存在相关性,根据图2中的几何关系及式(10)和式(11)得到:

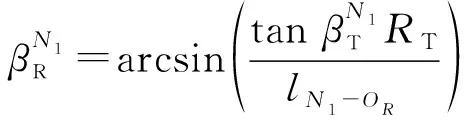
(12)

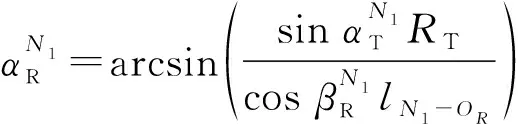
(13)

SB分量的多普勒频移和路径长度:

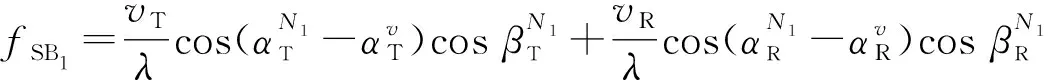
(14)

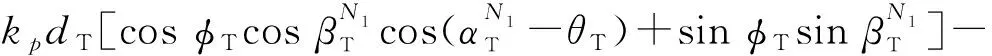
(15)

SB分量中,角度关系、多普勒频移和路径长度可分别表示为

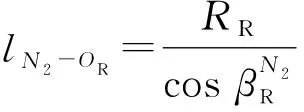
(16)

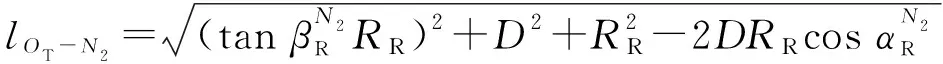
(17)

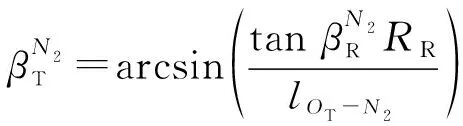
(18)

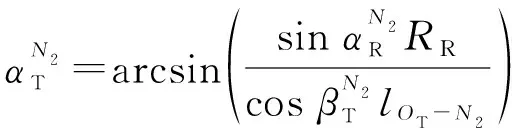
(19)

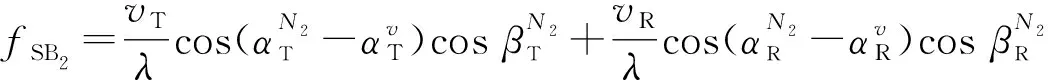
(20)

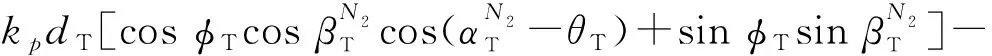
(21)

SB分量中,根据椭球的几何性质和余弦定理可以得到-,-:

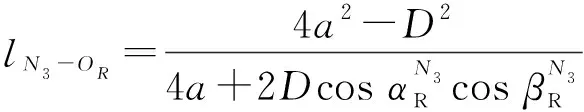
(22)

-=2--

(23)

其中，角度关系、多普勒频移和路径长度可表示为

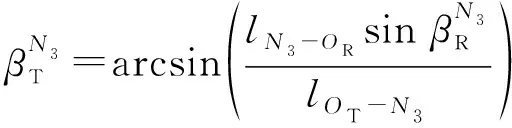
(24)

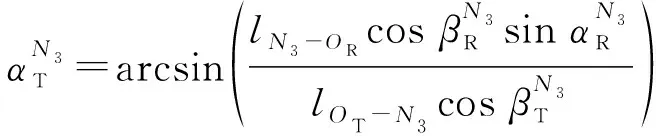
(25)

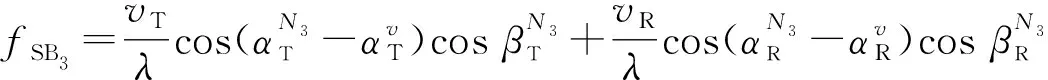
(26)

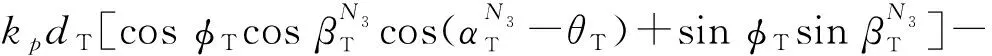
(27)

DB分量中,AAoD、AAoA、EAoD、EAoA相互独立,其多普勒频移和路径长度分别表示为

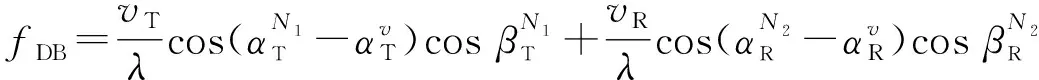
(28)

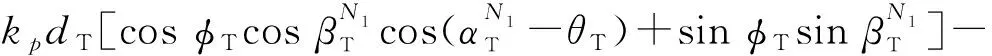
(29)

进一步考虑方位角和仰角对信道统计特性的影响。已有文献中采用了不同分布函数表征散射体分布,如均匀分布、Von-Mises分布和拉普拉斯分布等。其中Von-Mises分布能够通过调节相关参数近似成其他分布,达到模拟实际V2V通信场景中各种散射体分布情况。所以本文采用Von-Mises分布来描述方位角,用余弦分布来描述仰角：

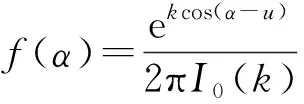
(30)

(31)

式中:代表方位角的均值；代表方位角集中于均值的程度；()是零阶第一类修正的贝塞尔函数。当=0时,散射体分布为均匀分布,符合各向同性散射环境。越大,方位角越集中于均值,散射体分布越趋于正态分布,符合各向异性散射环境。代表仰角的最大值,可以通过调节的值表征不同高度的散射体。

1.2 参考模型归一化空间-时间相关函数

实际V2V通信中,空间-时间相关函数(space time correlation function,STCF) 度量了V2V信道的时间和空间的统计特性,可用下式表示:

(32)

式中:E[·]代表期望函数；(·)代表复共轭。在参考模型中,有效散射体数目趋于无穷大,所以AAoD、AAoA、EAoD、EAoA可由连续变化的概率密度分布来表示。基于此,将式(32)表示为LoS分量、SB分量和DB分量归一化STCF的叠加:

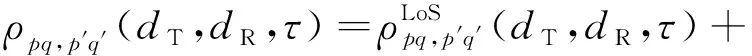
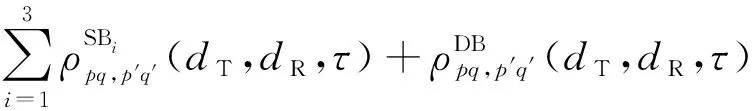
(33)

通过设置收发端天线阵列间距==0,可得到ACF:

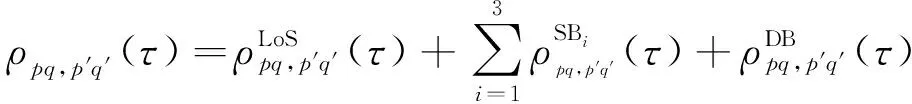
(34)

CCF反映两对不同收发端天线阵元之间信道的相关性,可以通过设置时间间隔=0得到:

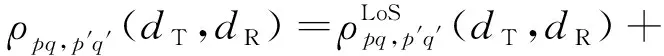
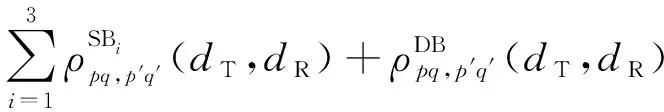
(35)

LoS分量的归一化STCF表示为

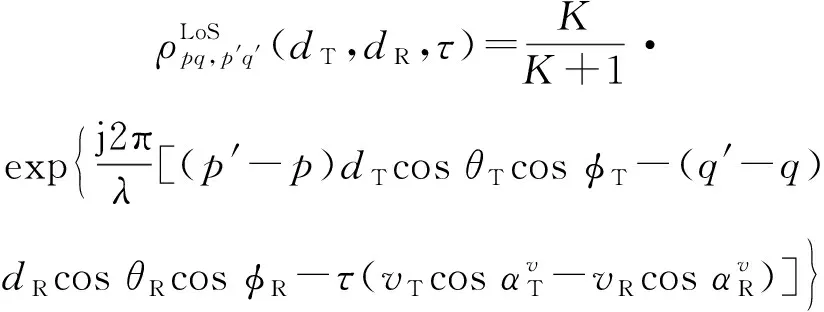
(36)

SB分量的归一化STCF表示为

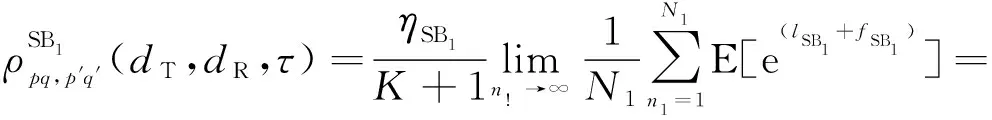
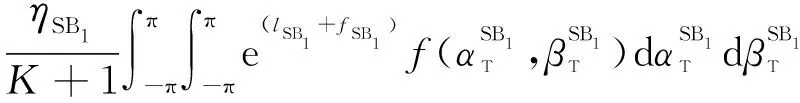
(37)

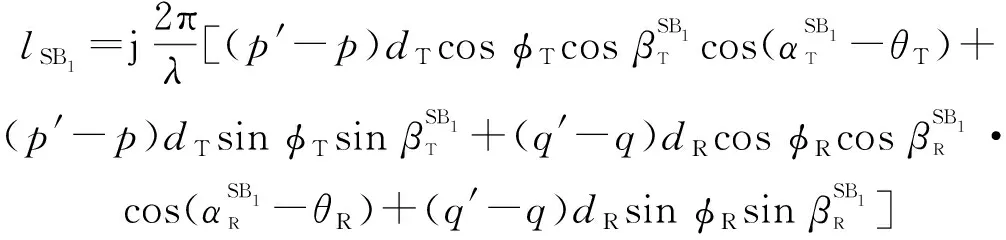
(38)

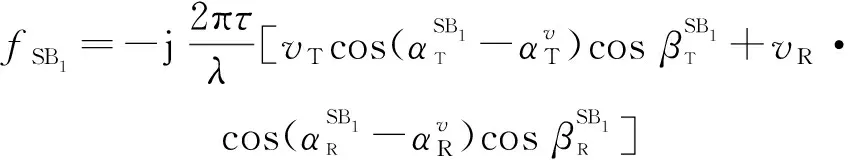
(39)

SB分量的归一化STCF表示为

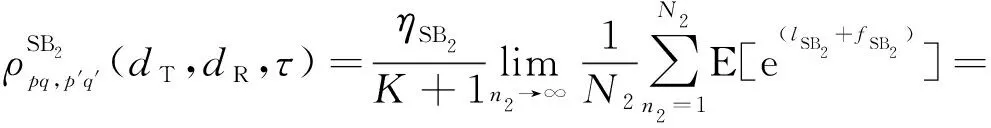
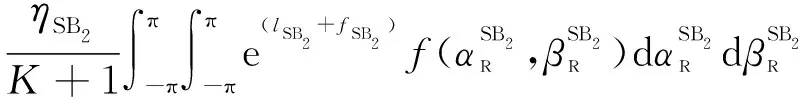
(40)

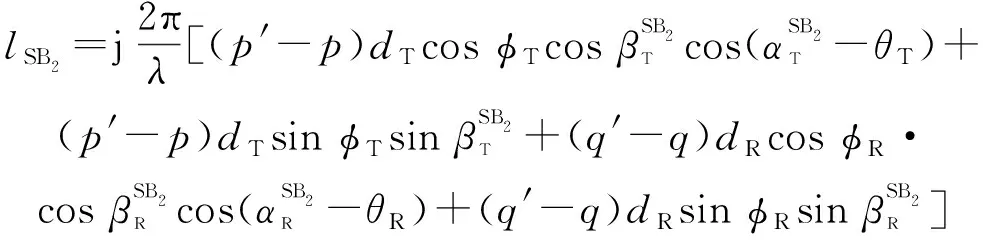
(41)

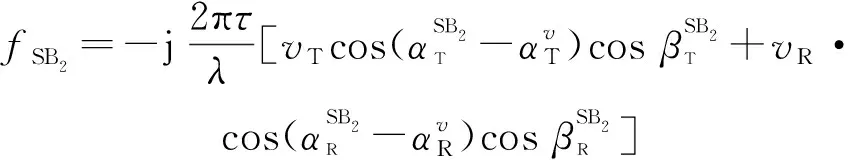
(42)

SB分量的归一化STCF表示为

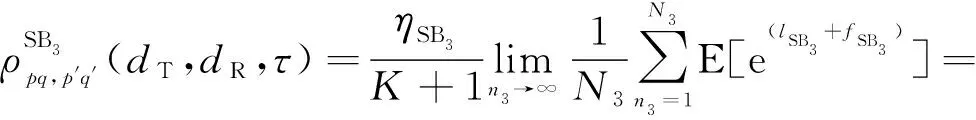
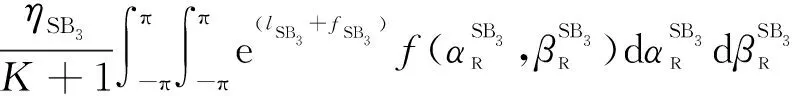
(43)

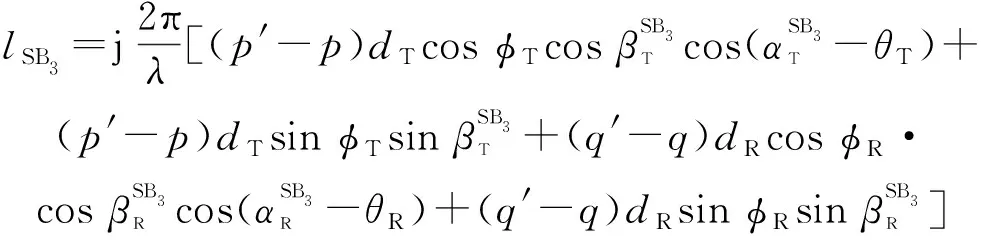
(44)

(45)

DB分量的归一化STCF表示为

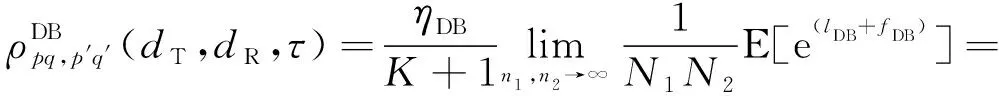
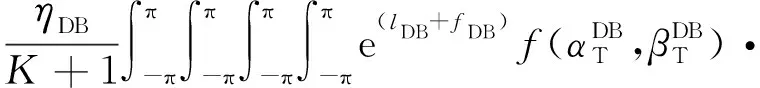
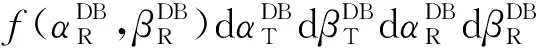
(46)

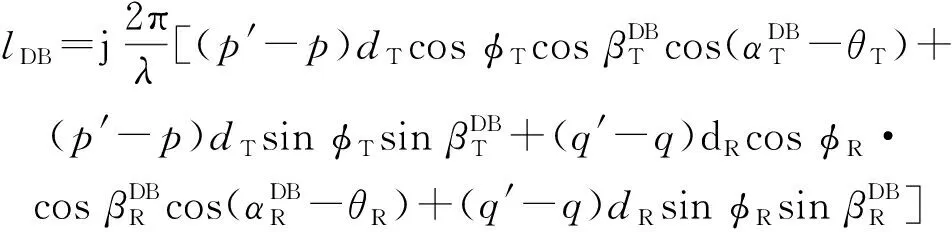
(47)

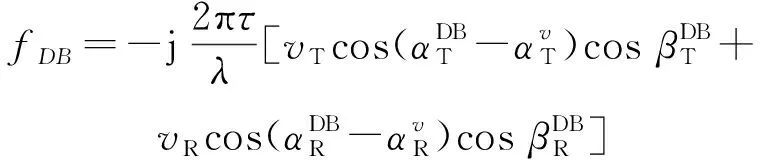
(48)

1.3 参考模型DPSD

在V2V信道中,信号通过不同的路径从T传播到R。除了信号包络和相位的波动外,接收到的信号频率也会因收发端的相对运动而不断变化。在此,定义()为所提三维MIMO V2V信道模型的DPSD,可由ACF的傅里叶变换表示为

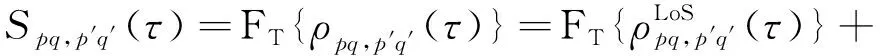
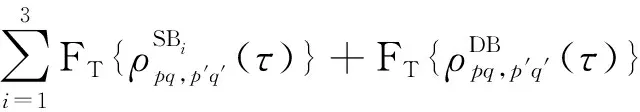
(49)

式中：F(·)表示傅里叶变换。

1.4 参考模型LCR和AFD

LCR和AFD是描述信道衰落的两个重要的二阶统计特性,可以反映动态多径衰落信道的时变特性。LCR的表达式如下:

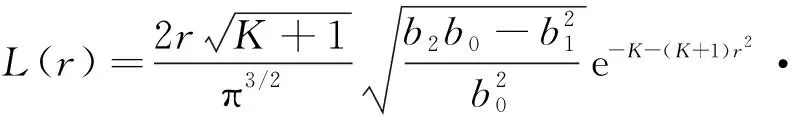
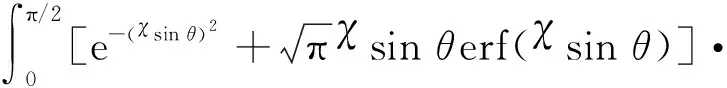
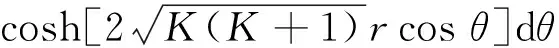
(50)

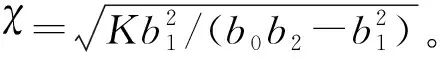
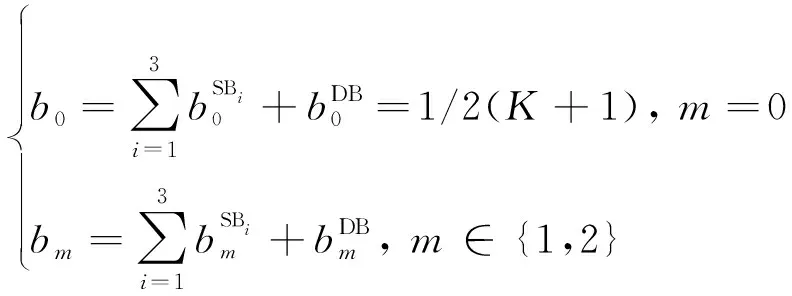
式中:

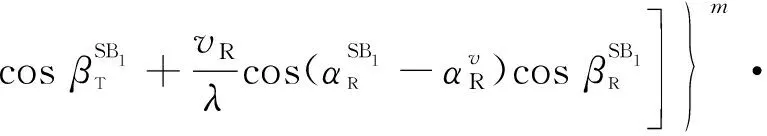
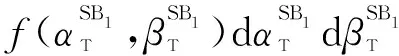
(51)

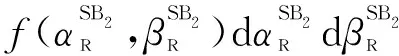
(52)

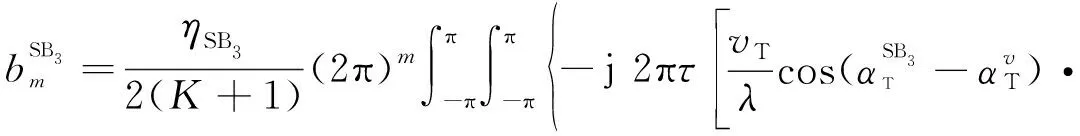
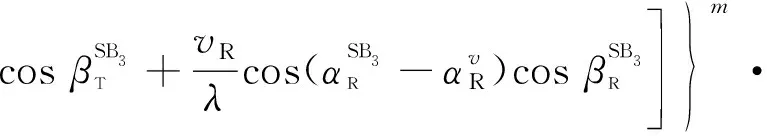
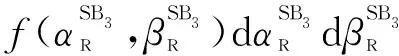
(53)

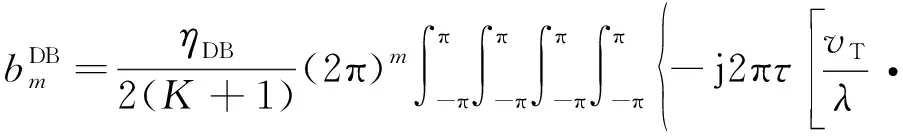
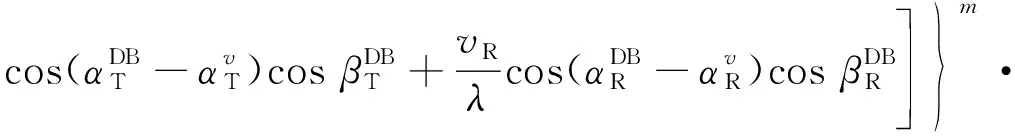
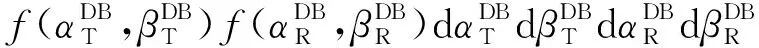
(54)

根据平均衰落持续时间()的定义,基于所提参考模型,得到AFD的表达式如下:

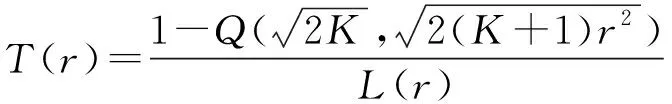
(55)

式中:(·,·)表示标准化的Marcum函数。

2 仿真模型

实际环境中有效散射体数目近似无限大, 这在参考模型中实现比较困难,因此引进仿真模型,通过确定有限数目的散射体和未知参数,可以较好地拟合参考模型的信道统计特性,大大降低系统的运算时间。

本文所建立的模型中离散的多普勒频率主要与AoD和AoA有关,因此需要确定的未知参数是AoD和AoA。本文采用修正等面积(modified equal area model,MMEA)算法仿真信号的AAoD、AAoA,用余弦分布算法仿真信号的EAoD、EAoA。离散的方位角由下式获得:

(56)

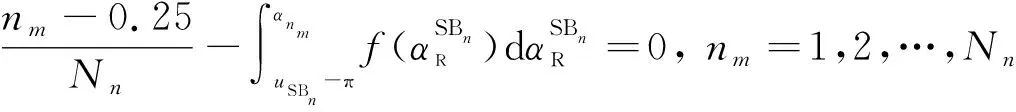
(57)

式中:代表围绕圆柱体和围绕椭球体有效散射体的个数;和是离散的AAoD和AAoA;SB和SB(=1,2)是AoD和AoA的均值。

离散的仰角由下式获得:

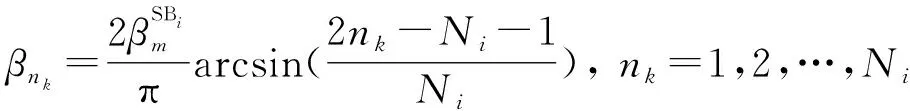
(58)

式中:代表围绕,圆柱体和围绕椭球体有效散射体的个数(=1,2,3);是离散的EAoD和EAoA。

为了验证仿真模型算法的可行性,本文以STCF的绝对误差作为拟合评估,定义为参考模型STCF和仿真模型STCF的差的绝对值:

(,,)=|(,,)-′(,,)|

(59)

3 数值仿真及验证

本文所选基本参数如下:=300 m,=400 m,==5 m,c=3×10m/s,=59 GHz,最大多普勒频移=100 Hz。

3.1 CCF结果分析

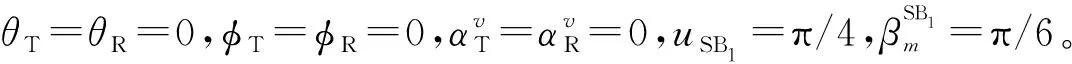
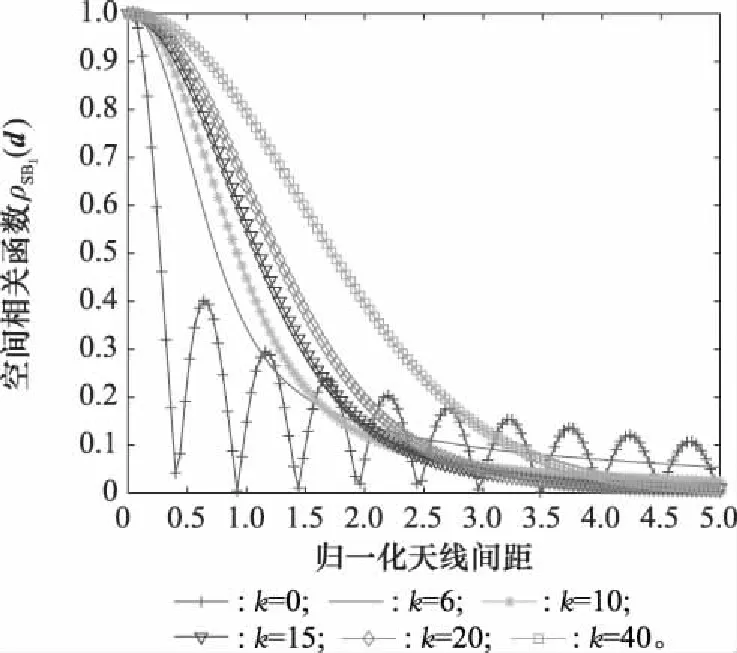
图3 k对SB1分量CCF的影响Fig.3 Influence of k on SB1 component CCF

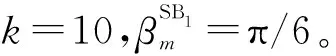
图4 uSB1对SB1分量CCF的影响Fig.4 Influence of uSB1on SB1 component CCF

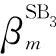
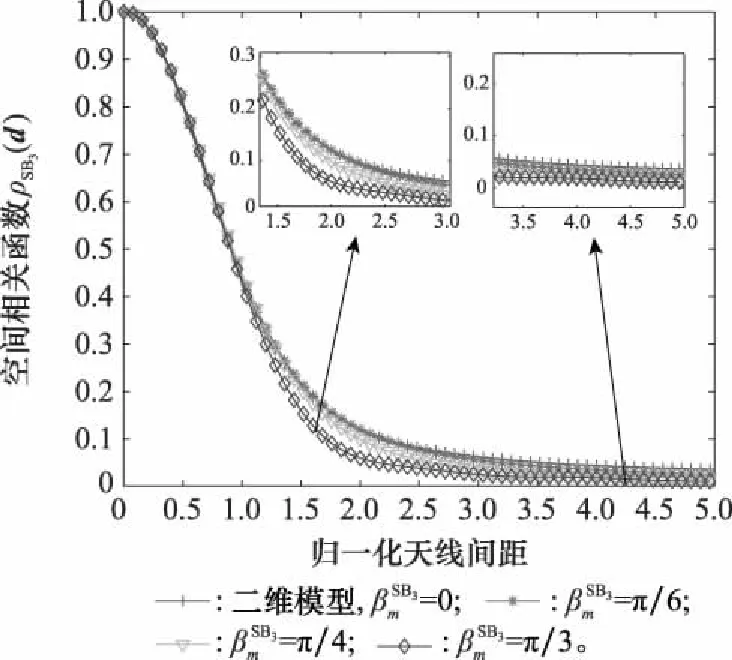
图5 对SB3分量CCF的影响Fig.5 Influence of on SB3 component CCF

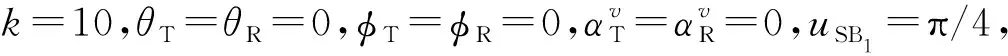
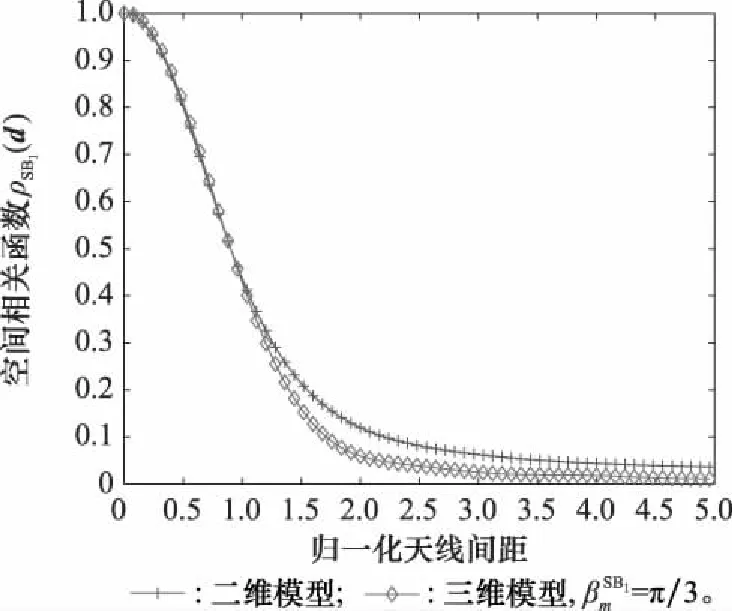
图6 二维模型和三维模型下对SB1分量CCF的影响Fig.6 Influence of on SB1component CCF under 2D model and 3D model

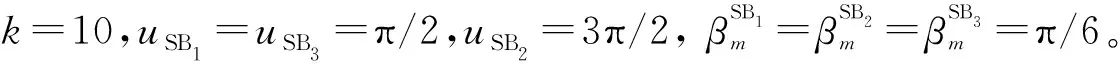
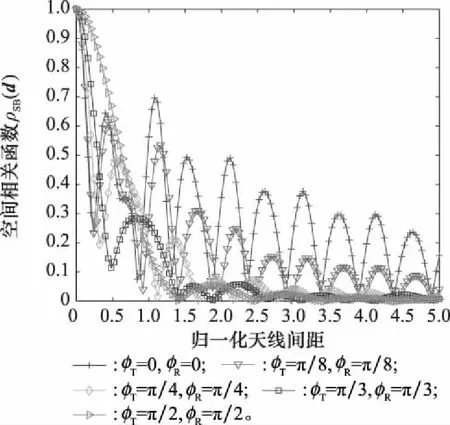
图7 φT、φR对信道CCF的影响Fig.7 Influence of φT and φR on channel CCF

综上,在V2V通信系统的设计中,不仅要考虑天线阵列间距对空间相关性的影响,还要考虑天线阵列的摆放方式,尽可能增大仰角以达到减小CCF、保证V2V通信可靠性的目的。

3.2 不同VTD下STCF结果分析

VTD反映了V2V实际场景中一条道路上车辆的密集程度,并且影响着V2V信道统计特性。根据文献[31]中的实测数据,不同VTD下的莱斯因子和功率系数如表2所示。

表2 不同VTD场景的关键参数Table 2 Key parameters of different VTD scenarios

低VTD场景中,莱斯因子较大,LoS分量占比最大,且SB>max{SB,SB}>,而对于高VTD场景,莱斯因子接近于0,LoS分量占比较小,这是由于密集的车辆和障碍物阻挡了LoS,并且满足>max{SB,SB}>SB。图8和图9分别表示低VTD和高VTD场景下的STCF。可以得出,低VTD下的STCF要高于高VTD下的STCF。

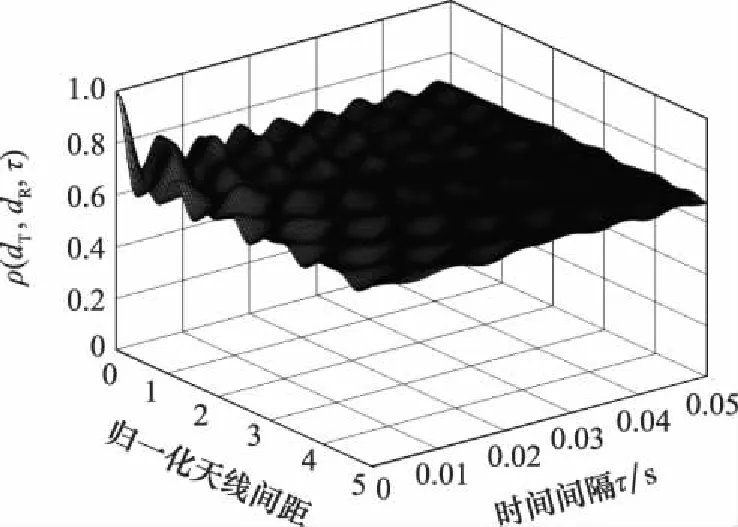
图8 低VTD下的STCFFig.8 STCF under low VTD

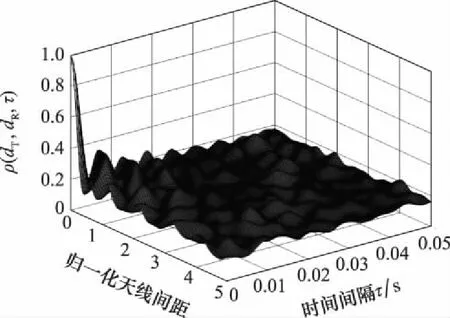
图9 高VTD下的STCFFig.9 STCF under high VTD

将本文三维模型与文献[10]中的二维模型的ACF和CCF作出对比,如图10和图11所示,可以得出高VTD和低VTD场景下本文三维模型与文献二维模型的CCF基本一致,证明了本文所提模型的合理性。但是当较大时,二维模型和三维模型的CCF还是有明显差异。这说明二维模型会高估信道的CCF,为了更好地设计V2V通信系统,应考虑仰角对其信道统计特性的影响。

图10 不同VTD下的三维模型和二维模型的ACFFig.10 ACF of 3D model and 2D model under different VTD

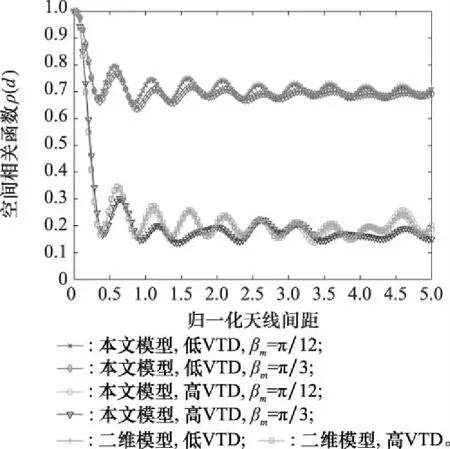
图11 不同VTD下的三维模型和二维模型的CCFFig.11 CCF of 3D model and 2D model under different VTD

3.3 仿真模型结果分析

考虑到模型的复杂度和仿真精度,本文假设有效散射体的数目为===40。

参考模型STCF和仿真模型STCF及其差异如图12～图14所示,参数选取=0。结果显示两者的误差几乎等于0,表明了仿真模型的STCF能较好地拟合参考模型的STCF,验证了仿真模型算法的有效性。

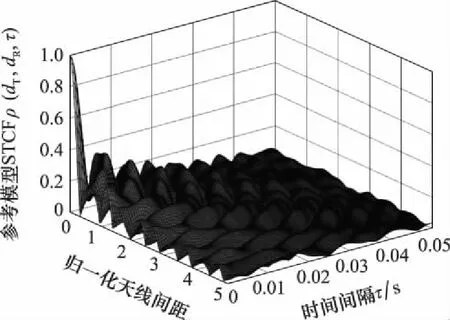
图12 参考模型STCFFig.12 Reference model STCF

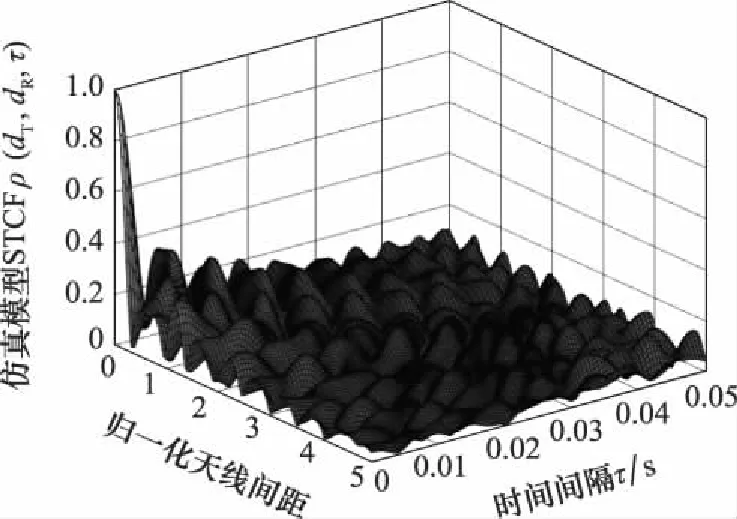
图13 仿真模型STCFFig.13 Simulation model STCF

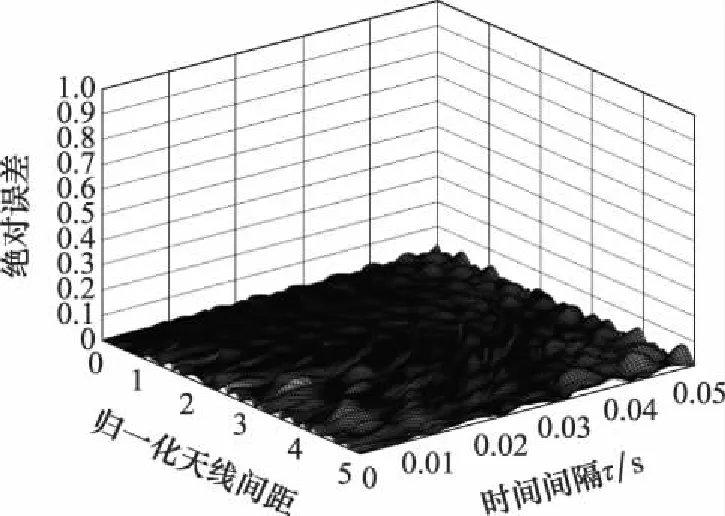
图14 STCF的绝对误差Fig.14 Absolute error of STCF

不同VTD下参考模型和仿真模型的ACF和CCF如图15和图16所示,参数选取表2实测数据,=0。结果显示无论是低VTD还是高VTD,ACF和CCF的仿真模型都较好地拟合了参考模型,并且低VTD显示出比高VTD下更好的拟合性,验证了所提仿真模型的合理性。

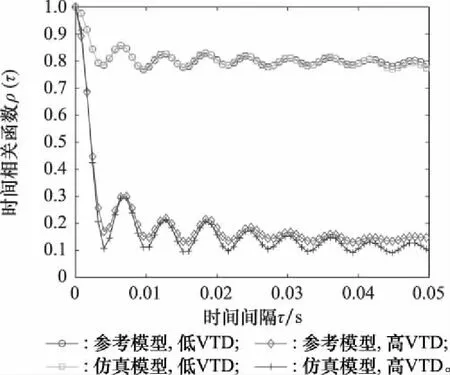
图15 不同VTD下参考模型和仿真模型的ACFFig.15 ACF of reference model and simulation model under different VTD

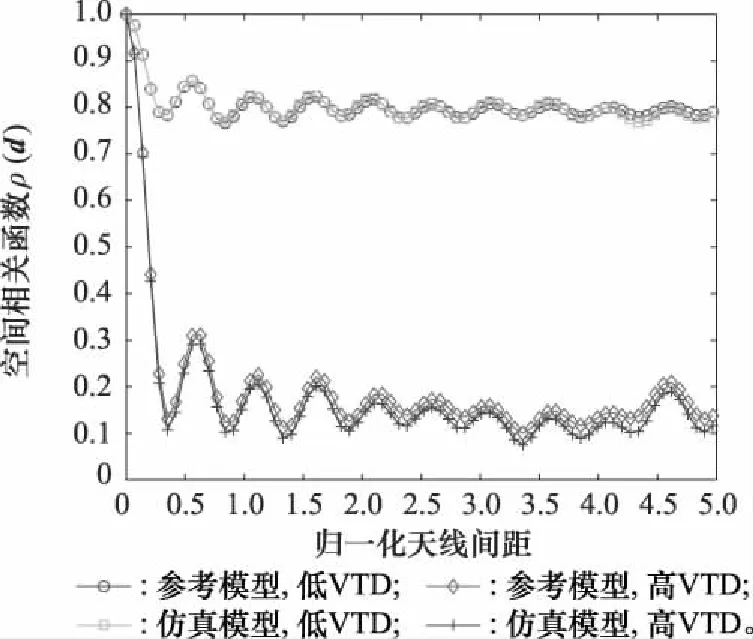
图16 不同VTD下参考模型和仿真模型的CCFFig.16 CCF of reference model and simulation model under different VTD

3.4 DPSD结果分析

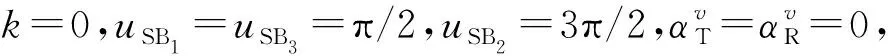
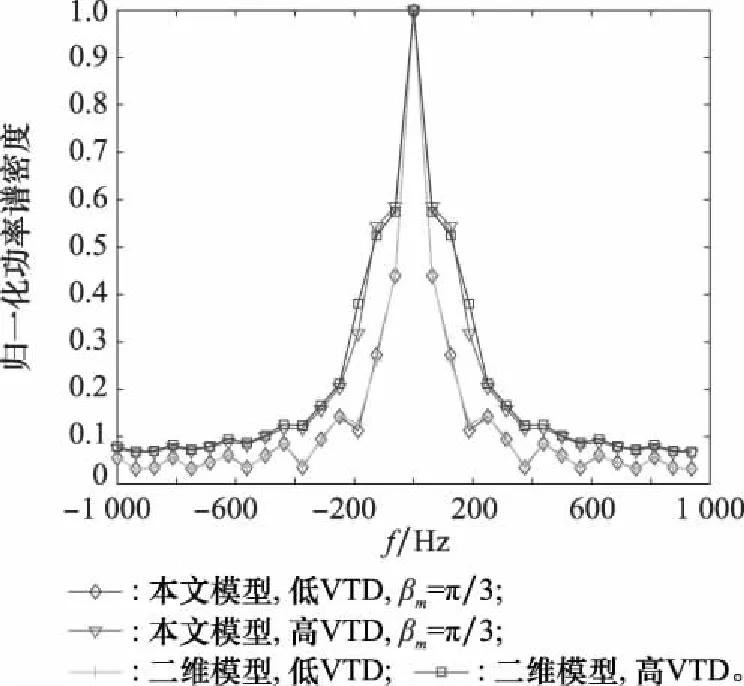
图17 不同VTD下二维模型和三维模型的归一化DPSDFig.17 Normalized DPSD of 2D model and 3D model under different VTD

不同VTD下参考模型和仿真模型的归一化DPSD如图18所示,参数选取表2实测数据,=0。结果表明,不同VTD下,仿真模型和参考模型DPSD的近乎一致性验证了仿真模型算法的有效性。

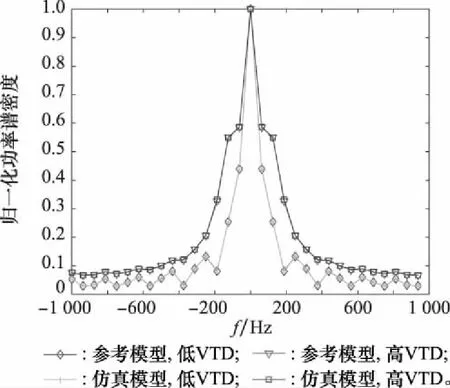
图18 不同VTD下参考模型和仿真模型的归一化DPSDFig.18 Normalized DPSD of reference model and simulation model under different VTD

3.5 不同VTD下LCR和AFD结果分析

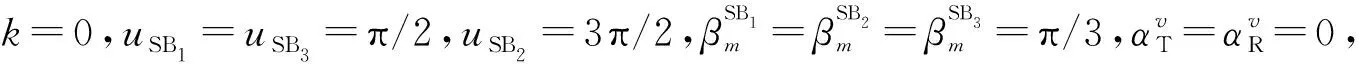
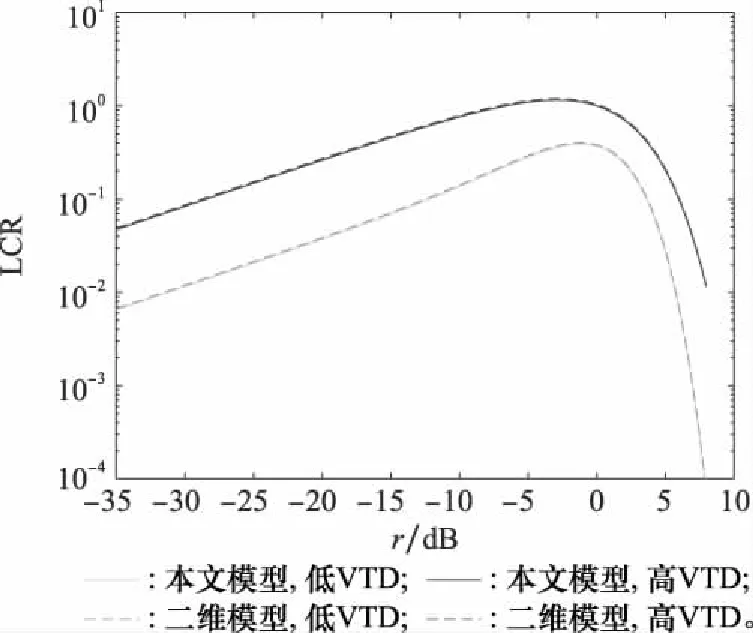
图19 不同VTD下二维模型和三维模型的LCRFig.19 LCR of 2D model and 3D model under different VTD

不同VTD下二维模型和三维模型的AFD如图20所示,选取参数与图19一致,可以看出VTD同样会显著影响AFD,由于AFD和LCR成反比关系,所以VTD低时,AFD较大,VTD高时,AFD较小。

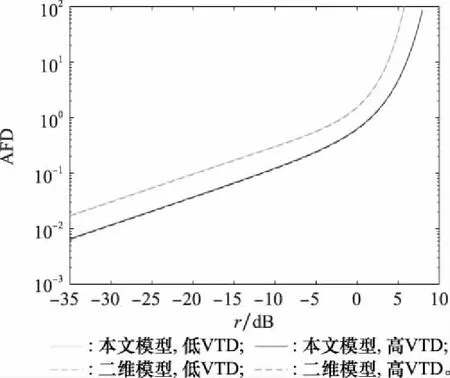
图20 不同VTD下二维模型和三维模型的AFDFig.20 AFD of 2D model and 3D model under different VTD

4 结 论

本文针对不同VTD下城市街道散射场景的MIMO莱斯衰落信道,提出一种新型的三维MIMO V2V GBSM,该模型结合了双圆柱模型和椭球模型,综合考虑了环境中移动和静止有效散射体的分布,能够研究各种实际场景下 VTD对信道统计特性的影响。本文根据模型推导了ACF、CCF、DPSD、LCR和AFD的理论表达式,分析了影响STCF的关键因素,并通过与二维模型的比较,研究了VTD和仰角对信道统计特性的影响,最后利用合理的参数计算方法建立了仿真模型。仿真结果表明:① 提出的参考模型是对已有三维模型的扩展,可以通过调节相关参数变量灵活适用于各种V2V实际通信场景;② 散射体分布、天线阵列排列方式综合作用于STCF,揭示了散射环境和天线阵列仰角对V2V MIMO系统的性能优化具有重要意义;③ 不同VTD对二维和三维的V2V信道统计特性有显著影响,低VTD场景始终显示出比高VTD场景更好的信道性能。本文模型扩展了V2V GBSM建模的方法,同时提供了一种易于实现的仿真模型,对车联网环境下车载无线通信系统的设计与评估具有一定的参考价值。