自适应杂交退火粒子群优化算法

路复宇, 童宁宁, 冯为可, 万鹏程

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

粒子群优化(particle swarm optimization, PSO)算法是由Kennedy等在1995年提出的新兴优化算法。由于其生物社会背景严谨、易于理解、参数较少且操作简单,对多峰函数问题和非线性问题具有良好的全局搜索能力,一经提出就引起了相关研究热潮,现已被广泛应用于模式识别、神经网络训练、路径规划、雷达资源调度优化、雷达图像处理、波达方向估计、天线方向图综合等领域。但是,标准PSO算法存在着早熟收敛、后期搜索速度较慢、收敛精度较低等问题。

针对上述问题,诸多学者对PSO算法进行了优化和改进。相关研究主要可以分为以下3类。

(1) 对PSO的惯性权重和加速系数等参数进行改进。例如,文献[12]基于个体适应度值和群体收敛信息划分种群,采用不同的自适应操作,使群体在进化过程中始终保持惯性权重的多样性,一定程度上解决了PSO算法早熟收敛问题。文献[13]在线性变化加速系数的基础上引入扰动加速因子,使部分粒子可以有选择地追随全局最优解,增强了算法的收敛速度及精度。

(2) 对粒子种群的邻域拓扑结构进行改进。例如,文献[14]从粒子获取信息的角度出发,基于个体极值中心点和全局极值点改进粒子的行为方式,提高了算法的收敛精度及稳定性。文献[15]采用集成学习的方法设计了一种混沌PSO算法,通过在6种混沌拓扑结构上的实验,验证了多混沌PSO算法的可行性。

(3) 利用其他智能优化算法对PSO算法进行改进。例如,文献[16]引入了基于离散正交交叉算子的免疫基因操作以及克隆算子,提高算法对多目标优化问题的有效性。文献[17]利用强化学习的方法自动调节参数,进一步提高了收敛速度和精度,为强化学习和群智能搜索算法的结合提供了一种新的方案。文献[19]融合了几种改进方式,提出了一种自适应模拟退火PSO(adaptive simulated annealing PSO, ASAPSO)算法,采用线性变化的加速系数,用双曲正切函数控制惯性权重,融合模拟退火算法提升算法跳出局部最优的能力,基于典型测试函数与5种改进PSO算法进行了对比,证明了该算法在寻优速度、收敛精度及稳定性等方面的优势。

然而,对于高维多峰函数,ASAPSO算法存在易陷入局部最优、寻优精度较差等问题。为解决这些问题,本文提出了一种自适应杂交退火PSO(adaptive hybrid annealing PSO,AHAPSO)算法。与ASAPSO算法相同,所提AHAPSO算法利用模拟退火算子提高粒子跳出局部最优的能力,增强前期搜索的全局性。所提算法不同的是:① 采用Sigmoid函数控制惯性权重,采用双曲正切函数控制加速系数,使得算法在面对高维多峰函数问题时具有较好的适应性,具备更优的全局搜索和局部寻优能力,降低前期陷入局部最优的可能性;② 在后期引入杂交变异算子,提高种群多样性,在保证原有最优解不被覆盖的情况下进一步寻优,提高收敛能力。基于文献[19]给出的3种典型测试函数对所提算法进行了验证,并与ASAPSO算法和标准PSO算法进行了对比。结果表明，所提算法在寻优精度和收敛速度上均具有一定优势。最后,将所提算法应用于天线方向图综合,获得了较好的性能。

1 标准PSO算法

对于复杂组合优化问题,牛顿法等传统优化算法需要遍历整个搜索空间,效率低且容易出现组合爆炸问题。受鸟类群体觅食行为的启发,Kennedy等提出了PSO算法,为解决搜索空间复杂庞大情况下的寻优问题提供了一种新的思路。

PSO算法在求解优化问题时,将问题的若干个潜在解抽象为粒子,寻优过程通过粒子在搜索空间内的飞行完成。每个粒子都有位置和速度两个特征,由被优化函数决定其适应度值。假定被优化函数的自变量空间为维,PSO的粒子总数为,则第个(=1,2,…,)粒子的位置和速度可分别表示为

=[1,2,…,]

(1)

=[1,2,…,]

(2)

粒子在每次迭代时的进化由3部分组成,分别是对上一次速度的继承、自身记忆和种群的信息交互。因此,第次迭代过程可表示为

(+1)=()+[()-()]+[()-()]

(3)

(+1)=()+(+1)

(4)

式中：为惯性权重系数；和分别是自身加速系数和社会加速系数,是控制PSO迭代的重要参数;()和()分别代表第个粒子在第维度上(=1,2,…,)第次迭代时的位置和速度;和为均匀分布在[0,1]之间的随机数;为粒子个体最优位置；为种群最佳位置。

粒子的搜索能力受到惯性权重系数和两个加速系数控制:控制粒子的惯性,决定粒子对上一次速度的继承比例;控制自我认知部分,指导粒子向该粒子自身的历史最佳位置飞行;控制社会认知部分,体现种群中各粒子的信息交换,指导粒子向种群最佳的位置飞行。在飞行过程中,粒子的位置范围和速度范围分别为[-,]和[-,]。算法经过参数初始化、适应度计算、粒子信息更新、终止条件判断等步骤,最终能够得到符合条件的解。

PSO算法结构简单、运行速度快,在处理复杂优化问题上具有一定的优势。但是,PSO算法的参数均为固定值,无法根据算法运行的程度进行自动调节,导致早熟收敛现象。此外,在进化后期,大量粒子聚集在一起,粒子速度会急剧降低,导致后期收敛速度较慢。同时,随着速度的降低,粒子很难跳出局部最优,导致收敛精度较低。

2 所提算法

为解决PSO算法易早熟收敛、后期速度较慢、收敛精度较低等问题,本文提出了AHAPSO算法,对惯性权重和加速系数进行自适应调节,并引入模拟退火算子和杂交变异算子提高算法精度。下面,分别对自适应惯性权重、自适应加速系数、模拟退火算子和杂交变异算子4个模块进行介绍,并给出所提算法的具体步骤。

2.1 自适应惯性权重

惯性权重用于控制PSO算法的开发和探索能力,其物理意义为粒子的惯性,即飞行过程中粒子对当前速度的继承比例。在实际优化过程中,一般希望粒子在前期具有良好的全局搜索能力,在后期具有较好的局部寻优能力,这就要求惯性权重在前期的取值较大,在后期的取值较小。Sigmoid函数在线性与非线性之间具有良好的平衡,可以满足惯性权重在算法各个阶段的需求。因此,本文选取[-,]之间的Sigmoid函数自适应控制惯性权重,表示为

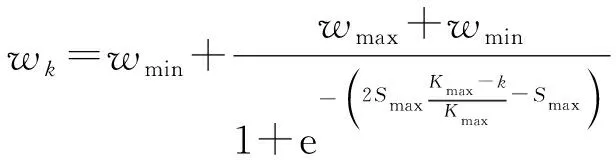
(5)

式中：和分别为惯性权重的最大值和最小值；为最大迭代次数；为当前迭代次数。

2.2 自适应加速系数

加速系数和分别调节粒子向个体最优和群体最优飞行的步长,决定了粒子自我认知和社会信息交流的权重关系。当>时,粒子更趋向于自身历史最优方向运动,反之则更趋向于群体最优方向运动。在算法初期,着重运动的遍历性,减小粒子陷入局部最优的概率,需要加大的比重;在算法后期,个体之间需要充分进行信息共享,着重在群体最优附近进行搜索,需要加大的比重。双曲正切函数可以随迭代的进行逐渐放大参数间的对比差异,其非线性特征可以使得粒子在前期充分进行全局搜索,在中后期迅速转入对群体最优附近空间的搜索。因此,本文选取[-,]之间的双曲正切函数对和进行自适应控制,表示为

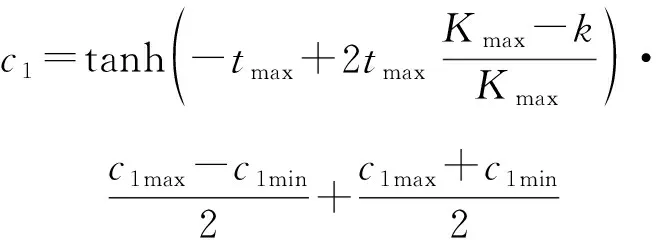
(6)

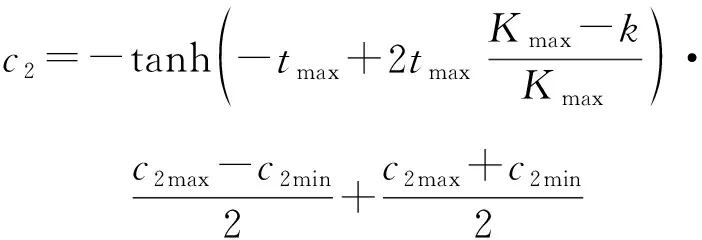
(7)

式中：和为自身加速系数的最大值和最小值;和为社会加速系数的最大值和最小值。

2.3 模拟退火算子

在面对复杂组合优化问题时,初始化的粒子往往很难分布在全局最优附近,加之PSO算法在前期有较强的收敛能力,从而导致算法很容易早熟收敛。为解决此问题,要求粒子能够在搜索空间内进行充分的探索,并且有能力跳出局部最优。因此,在更新群体最优的过程中引入模拟退火算子,使算法以一定概率接受差解,具备突跳能力,让一部分粒子朝最优解的反向运动,从而跳出局部最优,带动算法开展全局搜索。

首先,根据初始化信息确定温度,即

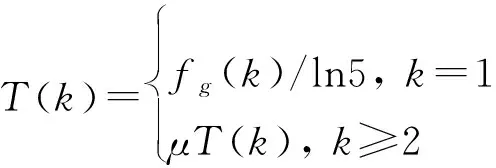
(8)

式中：()为每次迭代中的温度；为降温系数；()为第次迭代时群体最优粒子的适应度值。

然后,根据式(8)所确定的温度,计算接受差解的概率:

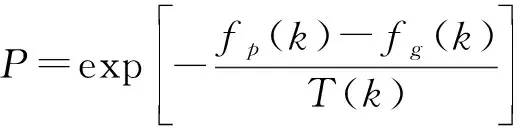
(9)

式中：()为粒子第次迭代后的个体最优位置的适应度值。

最后,根据Metropolis准则更新群体最优,表示为

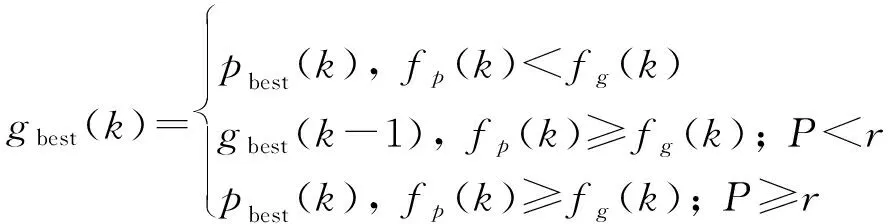
(10)

式中：为均匀分布在[0,1]之间的随机数。

2.4 杂交变异算子

随着算法的进行,大量粒子趋向同一,粒子种群多样性急剧下降,使得后期收敛速度明显下降,甚至无法继续优化。当种群多样性低于一定程度时,算法继续开发的难度较大,此时引入杂交变异算子来增加种群多样性,可以促进算法的进一步收敛。

首先,根据PSO体的平均中心距评判种群的多样性,表示为

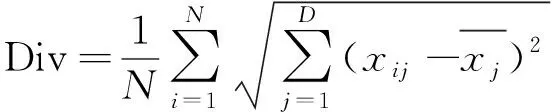
(11)

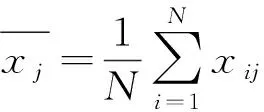
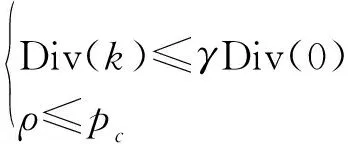
(12)

则对种群进行杂交变异操作。其中,Div()为第次迭代时的平均中心距,Div(0)为初始平均中心距,为杂交概率,为均匀分布在[0,1]之间的随机数,为阈值系数(通过对不同优化函数进行仿真分析可以发现,当迭代过程中的种群多样性下降为种群初始多样性的1%～5%时,粒子搜索能力下降,容易陷入局部最优。因此,在实际应用中,综合考虑收敛精度和收敛速度,一般可以将阈值系数取值为001～005)。

然后,根据杂交比例,在原始种群中随机选取个粒子进行杂交,产生子代粒子存入杂交池中,子代的位置和速度由父代随机交叉产生,表示为

(13)

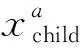
最后,为保留种群原始特性以及原有最优值,将原有群体最优粒子存入保留区,再从原始种群中随机抽取[(1-)-1]个粒子放入保留区,与杂交池内的子代粒子共同构成新的种群,新的种群将继续进行寻优。

2.5 算法步骤

基于以上4个模块,所提AHAPSO算法的具体步骤如下。

初始化、、、、、、、、等参数。

随机生成个粒子,初始化粒子个体最优位置和最优值、群体最优位置和最优值。

根据式(5)～式(7)自适应调整、和的值。

根据式(3)和式(4)更新粒子位置和速度。

对超出搜索空间和速度边界值的粒子进行边界处理,随机赋予一个边界内的值。

更新,并根据式(8)～式(10)更新。

根据式(11)和式(12)判断是否满足杂交条件,若不满足则返回步骤4。

根据式(13)执行杂交变异算子,产生新的种群。

记录本次迭代的群体最优及最优值。

判断算法是否达到最大迭代次数,若未达到则返回步骤3,若达到则输出当前最优结果。

3 实验结果及分析

为验证所提算法的性能,选取3种典型标准测试函数作为目标函数,取函数值为粒子适应度值,比较本文AHAPSO算法与ASAPSO算法和标准PSO算法的性能。此外,将所提算法应用在阵列天线方向图综合设计上,进一步验证其有效性。

3.1 测试函数及参数设置

所选取的3种典型标准测试函数具体信息如表1所示。其中,函数为较复杂的单峰函数,其在[1,1,…,1]处取得最优值0;为典型多峰函数,在搜索空间内存在多个局部最优值,在[1,1,…,1]处取得最优值0;函数为复杂多峰函数,搜索空间较大,多个峰值之间差异较小,在[420.968 7,420.968 7,…,420.968 7]处取得最优值0。由文献[19]结果可知,ASAPSO算法在各类测试函数下的效果较近年来其他同类算法均有较大优势,但在这3种函数上的测试结果与理论最优值还有一定的差距。

表1 3种典型标准测试函数Table 1 Three typical standard test functions

为保持实验结果的一致性,统一设置不同算法的种群规模为=30,最大迭代次数为=1 000。在所提AHAPSO算法中,=10,=08,=02,=4,=25,=125,=25,=125,=095,=1%,=08,=06,惯性权重和加速系数自适应变化曲线如图1所示。ASAPSO算法中的其余参数与文献[19]相同;标准PSO算法取=08,==15。

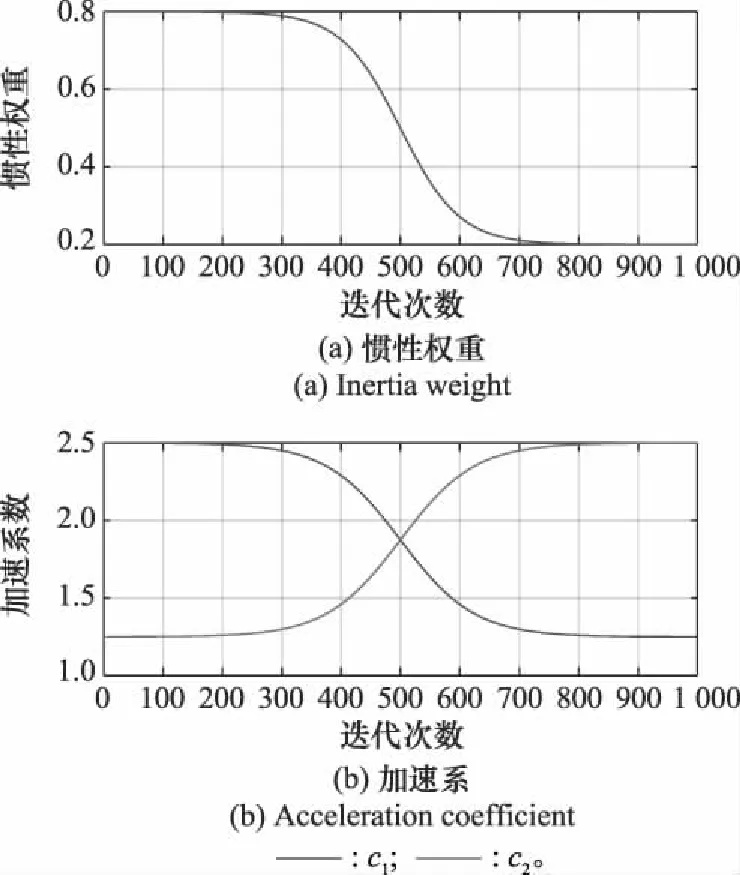
图1 惯性权重和加速系数自适应变化曲线Fig.1 Adaptive curve of inertia weight and acceleration coefficient

3.2 仿真结果比较

对于3种测试函数,分别在维度=10和=30条件下运行1 000次,记录不同算法所得结果的平均值(avg)和最小值(min),结果如表2所示。可以看出:① 所提算法对函数能够搜索到理论最优值,对和函数搜索得到的最优值也能够比较接近理论最优值;② 所提算法对3种函数得到的平均值和最优值均优于ASAPSO算法和PSO算法。结果表明,本文所提出的改进方法可以有效提高算法收敛精度。

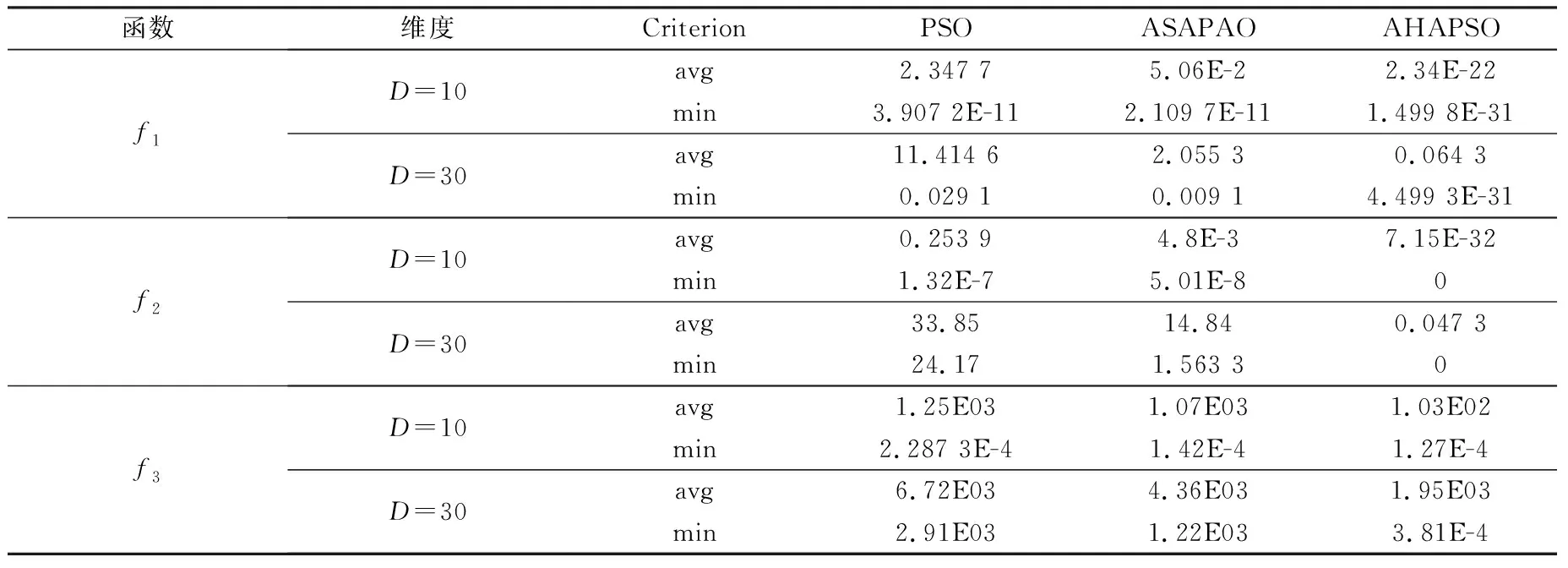
表2 PSO、ASAPSO和AHAPSO算法测试结果Table 2 Test results of PSO, ASAPSO, and AHAPSO algorithm

为比较3种算法的收敛速度,更加直观地体现算法精度,图2～图4给出了3种算法在不同函数下的适应度进化曲线(维度=30)。由图2和图3可知:① 在处理单峰函数以及复杂程度不高的多峰函数时,PSO算法收敛速度最快、精度最低,反映出PSO算法易早熟收敛、易陷入局部最优的问题;② 所提AHAPSO算法与ASAPSO算法在前期收敛速度均略有不足,主要原因是引入自适应参数变化和模拟退火算子,使粒子在搜索空间内充分探索,避免过早陷入局部最优,因此在前期收敛速度较慢;③ 在算法运行中后期,所提AHAPSO算法会有一个加速下探的过程,体现了杂交变异算子在中后期的主导作用,重新恢复多样性的粒子种群会加速寻优过程。由图4可知，在处理较为复杂的高维度多峰函数时,PSO算法在前期快速早熟收敛,ASAPSO算法虽在前期有较好性能,但中后期粒子停止探索,而所提AHAPSO算法在前期可保持较快收敛速度,中后期可进一步加速收敛,因此在整个运算过程中均具有较快速度。

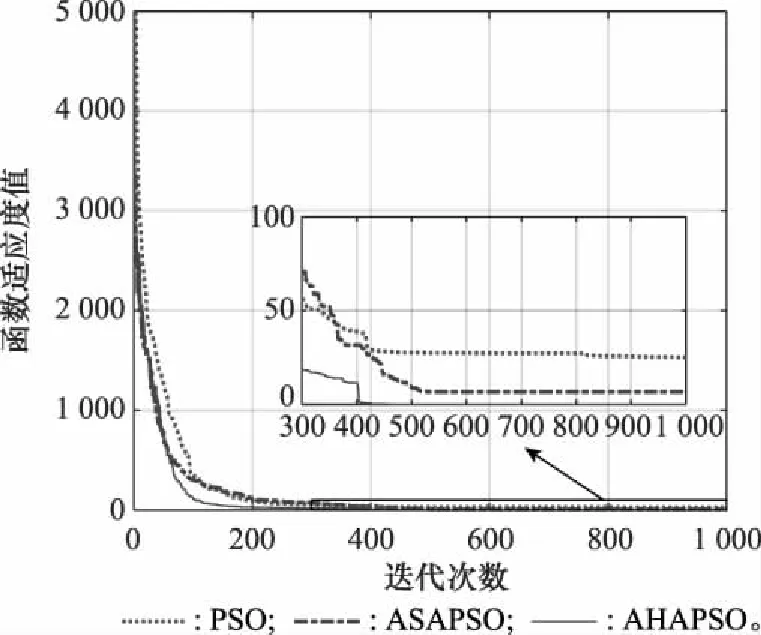
图2 f1函数下不同算法的收敛速度Fig.2 Convergence rate of different algorithms under f1 function

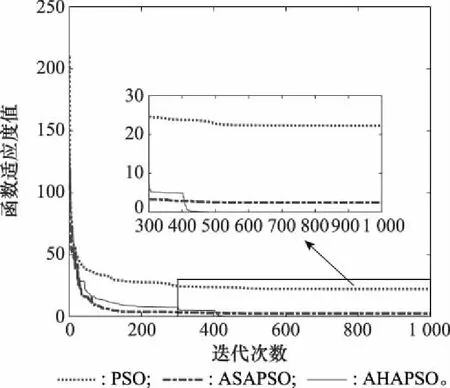
图3 f2函数下不同算法的收敛速度Fig.3 Convergence rate of different algorithms under f2 function

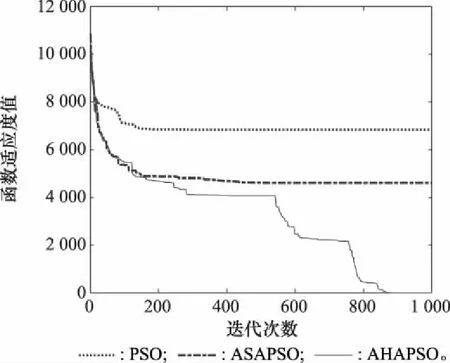
图4 f3函数下不同算法的收敛速度Fig.4 Convergence rate of different algorithms under f3 function

从实验结果可以看出,本文所提出的AHAPSO算法能有效解决PSO算法易早熟、后期收敛速度慢、收敛精度低等问题,在收敛速度与精度上均有较大优势。

3.3 阵列方向图综合设计

最后,为进一步验证所提算法的性能,将其应用于阵列天线方向图综合设计之中。根据天线阵理论,对于由个阵元组成的均匀直线阵列,若不考虑阵元之间的耦合,则该阵列的远场方向图函数可表示为

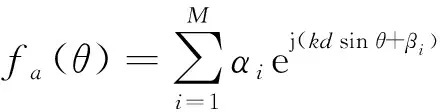
(14)

式中：为角度；和分别为第个阵元的幅度加权系数和相位；=2π为波数,为工作波长；为阵元间距。

由文献[30]可知,阵列方向图的最大旁瓣电平(maximum sidelobe level, MSLL)可表示为

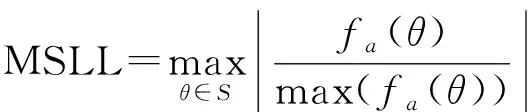
(15)

={|≤≤-∪+≤≤}

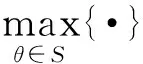
(16)

式中：为波束的指向；为主瓣零功率点；和分别为角度最小值和最大值。

利用PSO算法、ASAPSO算法和所提AHAPSO算法对一个阵元数=32、阵元间距=05的同相阵列进行设计,使其方向图的旁瓣电平最低。令32个阵元对称分布,设置每个粒子的维度为16,其余各参数均与第3.1节中相同,可得3种算法的最大旁瓣电平进化曲线如图5所示,阵列综合设计结果如图6所示。可以看出,所提AHAPSO算法在中后期具有更高的收敛速度和收敛精度,所得阵列方向图的最大旁瓣电平小于-47 dB,相比其他两种算法均有一定提高,验证了其优越性。

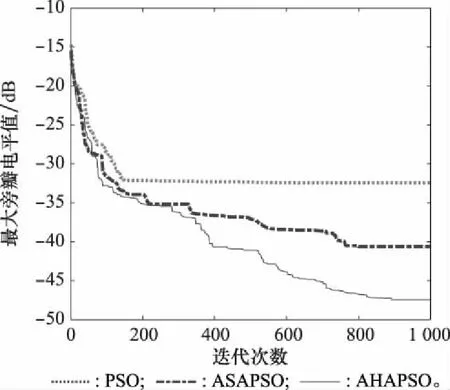
图5 不同算法的最大旁瓣电平收敛曲线Fig.5 MSLL convergence curve of different algorithms

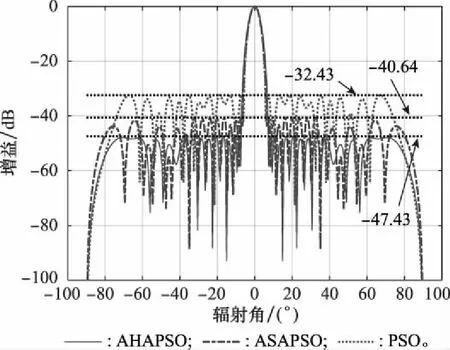
图6 不同算法优化得到的阵列方向图Fig.6 Array direction graph optimized by different algorithms

4 结 论

本文提出了一种AHAPSO算法,采用Sigmoid函数和双曲正切函数分别控制惯性权重和加速系数,引入模拟退火算子提高算法跳出局部最优能力,利用杂交变异算子提高后期寻优速度。3种典型标准测试函数的实验结果表明,所提算法相较于同类算法收敛精度和速度更高。在阵列方向图综合应用之中,本文所提算法可使得阵列方向图的最大旁瓣电平控制在-47 dB以下,进一步验证了其性能。