设置魔术教学环节 引导学生深度思考

◇郭琪霞（江苏：常州市新北区香槟湖小学）

数学魔术表现方式多样、新奇，尤其考量学生综合运用数学知识的思维、意识与能力。教师可将数学原理和数学思想带入魔术环节，帮助学生突破自我中心局限，培养学生的问题解决能力和数学创造性思维能力。因为数学魔术的观察、操作、探秘、揭秘环节的思维跨度较大，需要学生灵活切换看待数学问题的视角。教师在课堂上可通过“读心术”“透视眼”等看似神奇的魔术现象，集中学生的注意力，引领学生从多个角度分析探索，补充自己的逻辑盲点、深度思考的关键在于克服思维上的浅层意识，要让学生在处理“数学魔术”问题时，能超越直观、描述、记忆等浅显的认识，主动联系已有的认识经验，批判地、整体地关注问题核心奥秘。所以，对数学魔术的开发，要注重问题的解决和知识的应用。要让学生在寓教于乐的学习环境中，亲历“魔术”的观察、想象、假设、迁移、反思、应用，加深对数学知识的理解，体验不一样的数学趣味和学习精彩，进而使学生在一个有意义、有深度的思考与探究中，实现数学兴趣、数学思维与数学能力的综合发展。

一、变换思维视角，归纳猜想探究

数学魔术的趣味性、多变性、探究性，可以让学生在想象、运算的过程中掌握数学原理，体验学习乐趣。教师在课堂中可利用“数学魔术”启发思维，唤醒潜能，引导学生在观察、记录、思考、操作、讨论过程中运用批判性、跨越性思维灵活切换视角，独立思考，反复审视、分析，用数学的眼光，透过表象洞察“魔术现象”所隐含的数学原理。

例如，教学《倍数与因数》一课时，教师可结合归纳思想，用“数字读心术”联系“9 的倍数特征”，让学生依据乘法运算理解倍数和因数的含义，掌握求一个数的倍数的方法，提高学生数学的运算、归纳、思考能力。用“每个位置数相加之和可以整除9”“各位数字之和是9 的倍数”的9的倍数特征，观察“90，18，81，72，27，63，36，45，54”“1188，1+1+8+8=18，18 可以整除9，1188 是9 的倍数”现象。教师带入“数学魔术”要体现数学思想和数学原理，同时用可操作步骤和隐匿答案推动学生的思考前进，让学生在开阔的思维空间，亲身经历发现“9 的倍数特征”的探究思考过程。

教师：“从1 到10 随意想一个数字，想好以后将这个数字×9，如果得到1 位数，数字保持不变，如果得到2 位数，将个位、十位的两个数字相加，又得到1位数，最后将这个数字+4，头脑想一想，这个数字一定是13。”知识点隐藏于揭秘环节，“个位加十位等于9 的数能被9 整除，整数各个数位上的数字之和是9 的倍数。”教师要通过启发性问题给学生戴上一顶思考的帽子，引导学生在跨越式的思维变换中，联系2 的倍数特征、5的倍数特征、3 的倍数特征，探寻魔术背后数字“9”的变化和原理。

数学逻辑要知其然，更要知其所以然，这样才能触类旁通，举一反三。学生根据已学习的“3 的倍数特征”运算思考，知道通过各位数字的和，可以快速判断一个数能否被3 整除。比如：将2435=2×1000+4×100+3×10+5 继续拆分成2×(999+1)+4×(99+1)+3×(9+1)+5=2×999+4×99+3×9+()+()+()+()，剩余部分的数可以被3 整除，这个数就可以被3 整除。同理，“看各位数和”一样适用于能否被9 整除，而且9 的倍数特征，更容易与非0 自然数的个位数建立联系。教师用精彩的魔术现象，可以快速激活学生的数学思维，唤起其主动学习的动机，让学生在获取探索新知乐趣的基础上，经历观察、猜想、比较、归纳，提高数学认识迁移能力。

二、聚焦问题要点，协商反思提炼

教师在课堂中引入数学魔术，要为学生提供充足的思考实践空间，启发学生在有事实、有依据、有逻辑的“魔术”观察中，把数学知识灵活迁移到新的问题场景，实现数学思维与综合能力的提升。“魔术”是思维与技能的碰撞，目的是增强数学趣味，解决教材的疑点、难点。所以，课堂不应局限于教材知识传授，还要鼓励学生亲自参与、主动实践。要让学生在认识矛盾与思维经验的相互作用下，将所学知识融会贯通，重组数学经验结构，提高创新精神，让学生在数学实践中强化数学应用意识，提高运用知识技能解决问题的能力。

例如，教学《运算律》一课时，教师设计“骰子的原理”，同时整合自然数、小数、分数、负数、乘法、加法、图形与几何等数学知识，要求学生在实际问题的解答运算中，比较加法、乘法两种算法之间的联系，能用字母概括、表示数学规律，丰富空间概念，加深对各类数的认识。“教师背转，交由学生在圆筒内叠加5 个骰子，只能看到骰子顶部一面。学生可随意改变骰子叠加顺序，叠加完成后，说出顶部骰子数字。教师预测5 个骰子所有盖住面的点数，准确计算被盖住9 个面的和是多少。”

以验证(3+3+4+5+2+1+6+2+5=31)为例。原理：骰子的6 个面，每2 个对应面点数之和都是7。每个骰子的对面为“1 和6”“2 和5”“3 和4”，(1+6=3+4=2+5=7)，7 减去上面可见的点数，即是下方被盖面的点数。5 个骰子叠加，未知面点数之和=7×5 减去顶部可见面点数，即剩下9个面的和、教师要让学生成为一个发现者、实践者、探究者，鼓励学生根据发现的规律，自制骰子、抛骰子，探索“骰子未知面的点数”，让学生通过问题的挖掘自主计算，加深对数学知识的理解和认识。教师：“观察骰子形状，根据发现规律制作骰子。”“你能抛出几种不同方法？用算式计算记录骰子的秘密。”教师同时向学生呈现展开图，组织学生以小组合作形式观察制作骰子，把骰子看成一个正方体。

“数学魔术”奥秘要与教学目标紧密结合。要以自主、合作、探究为学习方向，引导学生亲身体验操作，在6 个展开图平面填写点数，观察点数分布，自主归纳、概括，建立严谨的思维逻辑链。

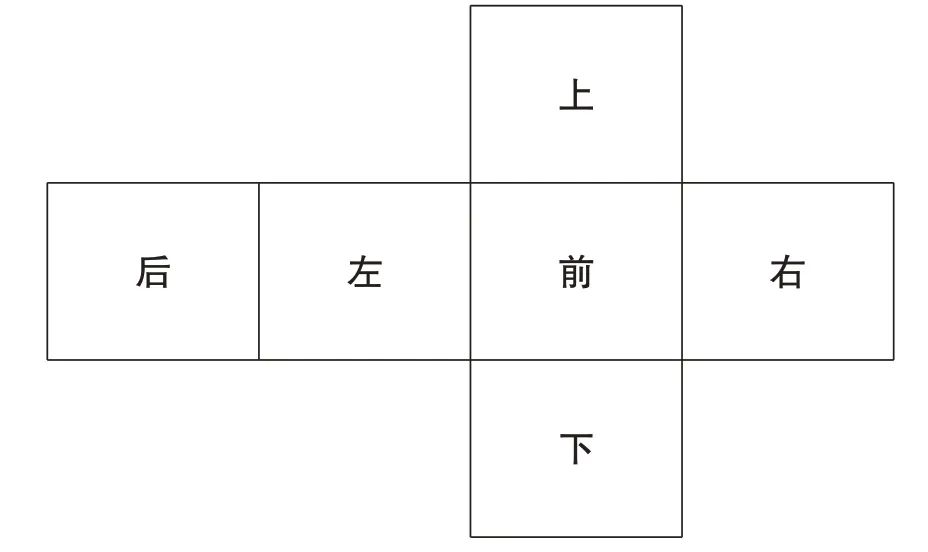
观察平面图上面、下面()+();左面、右面()+();前面、后面()+();概括成相对面的点数和是多少()。学生自主列式计算，破解魔术原理，思考：从上往下看，看不到() 面，根据点数的和7，可推算出这个面点数是()，剩余4 个骰子看不见的面是()面和()面，所以骰子看不见的点数和是()，并且自己列式计算。

学生预测骰子未知面的点数，需要掌握3 个条件，骰子相对面点数和是“7”不变，无论怎样叠加，5 个骰子相对面和永远是35，顶部点数随着不同叠法变化，35 减顶部点数即可。教师在学生掌握数学原理后，可设置“魔术畅想”环节，要求学生重新设计骰子相对面和。教师：“你有更神奇的设计吗？”“如果相对面的和是10 或1 或0，需要怎样计算？”引发学生的奇思妙想，让学生在交流中运用学习过的小数、分数、负数、倒数等知识解决实际问题，锻炼学生数学应用意识和创新思维能力。

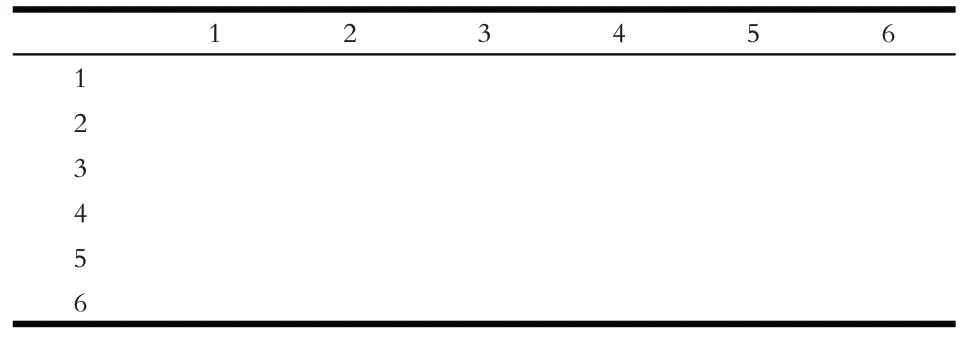
骰子是最易产生随机数的工具，教师可组织学生自己动手创新玩法，利用骰子的概率问题拓展数学猜想空间，让学生同时投掷2 颗骰子，在表中记录面朝上的点数和，看看有多少种可能性。教师还可要求学生计算看不见面数的乘积，丰富学生的空间概念，引导学生在列表、检验、估算、质疑、验证和交流中积蓄数学经验，发展思维逻辑性和严谨性。

三、深层逻辑论证，辨别假设抽离

教师在课堂要以“魔术问题”为纽带，指导学生自主搜集资料，提炼要点，独立制定“魔术解密”方案。让学生在方案的执行中相互协商、操作、反思，参考不同的立场、观点，主动整合散乱、孤立的信息，收获完整的数学经验。“数学魔术”的功能在于激发动机情感，引发思考猜想，驱动学生在观察、探究与实践中合理推测，破解思维疑问，发展数学能力。所以，“魔术”要将学生置于一个完整的问题背景中，要求学生从不同角度分析“事物现象”传达的信息，自主完成识别问题、分析问题、解决问题的动态思考与数学知识深度建构。

例如，教学《简易方程》一课时，教师要求学生想一个数，学生自己对这个数进行运算，得到另一个数，然后说出运算规则和得到的另一个数，教师猜测学生心里的那个数是多少，教师：“心里想一个数×2，然后+20，=？”学生：“80。”教师：“你想到的数是30。”这里融合了逆推法和划归思想、学生想的数是“×2+20=80”，设这个数为，“2+20=80，2=60，=30”，“2×30+20=80，=30”。教师：“把你心里想的数×3，-30，=？”学生：“100。”“-20=100”，设学生心里想的数为，“3-20=100，3-20+20=100+20，3=120，3÷3=120÷3，=40”所以，学生想的数是“40”。教师可为学生提供一个趣味魔术情境，组织学生根据规则，向有意义的方向提出疑问，要求学生自主查找关键数学信息，将数学知识点和数学思想串联思维的逻辑链条，延伸思维广度、深度，筛选出自己内心“想要的解题方法”，而不是“需要的解题方法”。引导学生在从容的思考和行动中，根据等量关系列方程、检验、解方程，体会代数思想、归化思想，更进一步认识用字母表示数的意义，明确解方程、方程的解等相关概念。让学生在趣味环节的思考实践中，锻炼缜密的思维，提高选择算法的意识和用列方程的方法解决问题的能力。

总之，数学魔术有助于知识的延伸和拓展，可以让学生在思考问题的过程中，通过新旧知识的整合迁移，形成解释问题的数学思路。虽然魔术与数学的结合表现形式可以带给学生新奇的体验和强烈视觉冲击，但数学思考往往深藏于背后的隐秘中.所以，教师要支持学生独立观察、操作，用“魔术”将学生的思维引向更广阔的探索空间，让学生在奥秘探索中能广泛联系自身经验、知识、技能，多角度洞察问题，解析魔术与数学原理间的内在联系，进而让学生在敏锐观察、探讨、解释、交流中亲历知识的形成与发展，实现数学素养和思维能力的锻炼与提升。