基于几何扩展卡尔曼滤波的四旋翼位姿估计算法*

成利梅，崔晋龙

(1.太原科技大学，山西 太原 030024；2.国网山西送变电工程有限公司,山西 太原 033000)

0 引言

四旋翼飞行器因其高度的灵活性和机动性得到广泛研究和应用[1,2]，而位置和姿态的准确测量是四旋翼实现自主飞行的重要基础。

惯性导航系统(INS)通过惯性测量单元(IMU)的测量能以较高的频率解算得到飞行器的位置和姿态，但IMU在长期测量中存在明显的漂移误差，测量精度较低[3]。GPS测量精度较高，没有误差积累和漂移现象，但其更新速率较慢[4]。因此，将惯性导航系统和GPS进行组合来获取飞行器的位置和姿态可以实现优势互补。

卡尔曼滤波(EKF)[5，6]、无迹卡尔曼(UKF)滤波[7，8]和其他非线性优化方法均在组合导航中具有良好性能。其中，扩展卡尔曼滤波是实践中最实用的方法。然而在传统的扩展卡尔曼滤波中选取四元数描述姿态，没有解决四元数的归一化问题[9]。近年来，直接采用旋转矩阵表示姿态的方法避免了四元数表示姿态的过参数和归一化问题。

采用间接法的卡尔曼滤波以误差量作为状态量，但IMU误差量是由真实值和估计值直接求差获得，并没有考虑两个向量是在不同的坐标系下表示的。针对IMU误差坐标系的一致性问题，基于误差一致性表示的几何EKF(GEKF)[10，11]被提出，通过几何变换将误差表示在同一坐标系下。最近，常路宾研究了基于SE(3)的扩展卡尔曼滤波姿态估计算法[12]，该研究采用旋转矩阵描述姿态，并将陀螺仪偏差描述在同一坐标系，但该研究仅考虑了姿态估计。本文将基于误差一致性的位置估计加入状态估计，实现了飞行器的位姿估计。

1 系统模型

对于四旋翼飞行器而言，位置和姿态信息为控制器提供反馈信息，位置和姿态的测量精度将影响控制器的控制效果。惯性导航系统通过惯性传感器测量机体的加速度和角速度，然后通过解算获得机体的位置、姿态信息。GPS通过测量可得到机体的位置信息。

1.1 惯性传感器数学模型

在惯性导航系统中，常用加速度计测量机体的加速度，用陀螺仪测量机体的角速度，加速度计和陀螺仪的数学模型[13]满足：

(1)

其中:am和ωm分别为加速度计和陀螺仪的测量输出；ab和ωb分别为真实的加速度和角速度；wa和wg分别为加速度计和陀螺仪的零均值高斯白噪声；εa和εg分别为加速度计和陀螺仪的常值漂移，其满足如下方程:

(2)

其中:ζa和ζg分别为加速度计和陀螺仪的随机游走，为零均值高斯白噪声。

1.2 位置姿态解算

为了描述四旋翼的位置和姿态，需要先建立两个坐标系——参考坐标系和载体坐标系。四旋翼的位置可由其质心在参考坐标系下的向量描述，姿态可由参考坐标系和载体坐标系之间的旋转矩阵描述。若旋转矩阵R∈SO(3)表示载体坐标系到参考坐标系的旋转矩阵，则其对应的指数形式[14]为：

R=eφ×.

(3)

其中:φ=θα为李群R∈SO(3)所对应的李代数，θ为旋转角度，a为旋转轴对应的单位向量。

同时，旋转矩阵的微分满足：

(4)

其中：ωb为载体的旋转角速度。

由于加速度计测量得到的是机体在载体坐标系下的加速度，因此需要将加速度通过旋转矩阵转换到参考坐标系，机体在参考坐标系下的位置和速度满足:

(5)

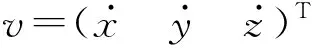
1.3 GPS测量模型

GPS系统能够输出机体在参考坐标系下的位置，其测量模型满足:

Z=p+V.

(6)

其中：Z为GPS的输出；V为测量噪声，为零均值高斯白噪声。

由于惯性传感器的输出存在漂移，因此基于惯性传感器解算获得的机体导航信息误差会随着时间累积，不适合于长时间的定位。GPS输出精度较高，但数据更新速率较慢。本设计通过卡尔曼滤波对两个系统的输出信息进行融合,以得到更为准确的位置姿态信息。

2 INS/GPS几何扩展卡尔曼滤波算法

2.1 状态变量与状态方程

本系统对机体的位置、速度、姿态以及加速度计和陀螺仪的漂移进行估计，定义状态量X=(pTvTRTεaTεgT)T。本文先对状态量的误差进行估计，用估计得出的误差量进一步修正状态量。

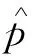
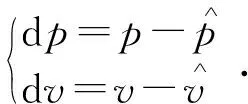
(7)

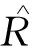
(8)

将式(8)表示成指数形式可得:

(9)

将式(9)展开，可得旋转矩阵误差的一阶近似值为:

(10)

其中：I为单位矩阵。

基于式(10)定义旋转矩阵误差的向量形式如下:

(11)

当估计载体坐标系趋于载体坐标系时，dφ则趋于0。

(12)

结合式(7)、式(11)、式(12)定义如下状态误差矢量:

dX=(dpTdvTdφTdεaTdεgT)T.

(13)

将式(13)中的每一项求导可得:

(14)

结合式(4)和式(5)可得状态量的估计值满足:

(15)

将式(2)、式(4)、式(5)、式(15)代入式(14)可得:

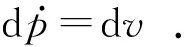
(16)

(17)

(18)

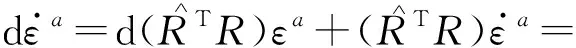
(19)

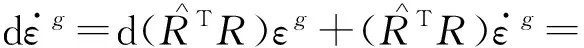
(20)

将式(16)～式(20)整理可得基于误差矢量的状态方程为:

(21)

式(21)中:

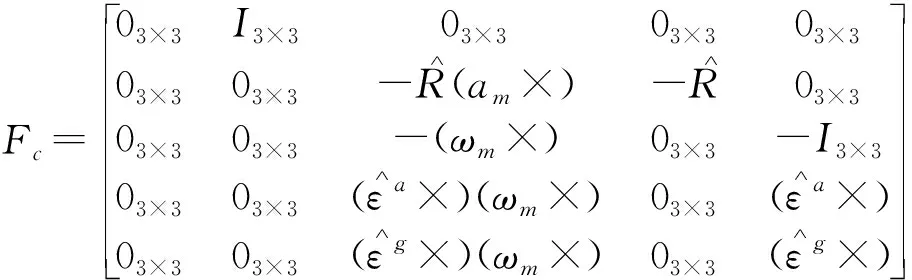
(22)

(23)

(24)

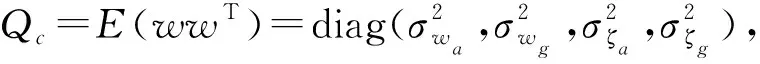
采用前向欧拉法对状态方程(21)进行离散可得离散化之后的状态方程，k时刻的状态方程为:

dXk+1=FdXk+Gwk.

(25)

式(25)中:

F=I+FcΔt.

(26)

G=GcΔt.

(27)

其中：Δt为采样时间间隔。

2.2 量测方程

我们选取GPS输出的位置作为系统的观测量，结合式(6)可得系统的测量方程为:

Zk=HXk+Vk.

(28)

其中：Zk为k时刻的位置测量值;Xk为k时刻的状态量；H=(I3×303×12);Vk为测量噪声。

2.3 信息融合机制

综上，式(25)和式(28)构成了卡尔曼滤波器的状态方程与量测方程。

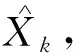
Xk+1|k=

(29)

(30)

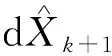
Kk+1=Pk+1|kHT[HPk+1|kHT+Sk+1]-1.

(31)

其中：Sk+1为测量噪声Vk+1的协方差矩阵。

此时状态误差的更新为:

(32)

误差协方差的更新为:

Pk+1=[I-Kk+1Hk+1]Pk+1|k.

(33)

结合式(13)、式(29)和式(32)可得:

(34)

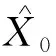
在实际系统中，陀螺仪和加速度计的采样速率为100 Hz，而GPS系统的采样速率约为1 Hz，两者速率不匹配。在本文中，当GPS测量更新时，融合两者数据更新状态量，其他时刻采用状态的预测值作为系统的输出。滤波算法的流程如下所示:

if IMU采样到第k次数据 then

end

if GPS测量更新 then

Kk+1=Pk+1|kHT[HPk+1|kHT+Sk+1]-1

Pk+1=[I-Kk+1Hk+1]Pk+1|k

else

Pk+1=Pk+1|k

end

3 仿真验证

为了验证所设计算法的有效性，我们在MATLAB环境下进行仿真验证[15]。整体的仿真流程如图1所示。轨迹发生器生成对应位置和姿态轨迹的理想加速度和角速度数据，模拟惯性传感器模块按照式(1)对理想加速度和角速度加噪声后输出到所设计的滤波器，滤波器最后输出状态量的估计值。

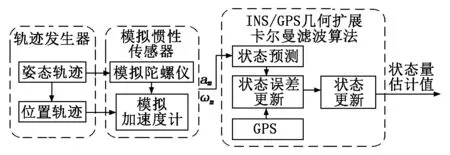
图1 仿真系统流程图

陀螺仪和加速度计的性能参数如表1所示。

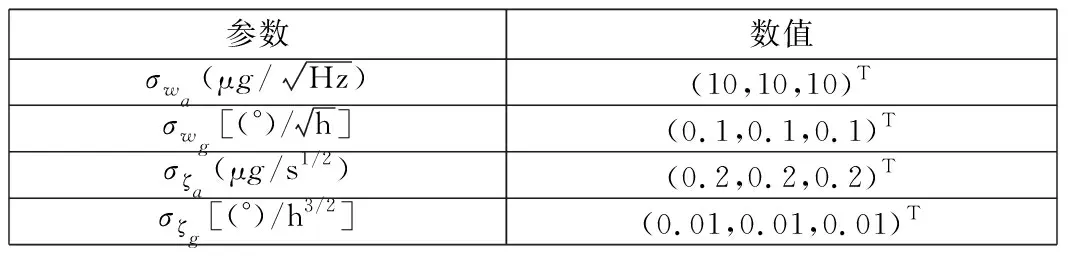
表1 陀螺仪与加速度计性能参数

由表1可知，系统的过程噪声协方差矩阵Qc=diag(100 100 100 0.01 0.01 0.01 0.04 0.04 0.04 0.000 1 0.000 1 0.000 1)。假设测量噪声协方差矩阵S=diag(0.0120.0120.012)。

仿真过程中，采样周期Δt=0.01 s，仿真时间t=100 s。

图2和图3分别为系统在所设计算法作用下的位置估计误差和速度估计误差。由图2和图3可知，三个方向的位置以及速度估计误差均稳定在零的附近。图4为姿态角估计误差，由欧拉角(Φ,Θ,Ψ)误差表示。从图4中可得，欧拉角误差在±5°以内。综上可得，所设计的算法可较好地实现四旋翼位置和姿态的估计。

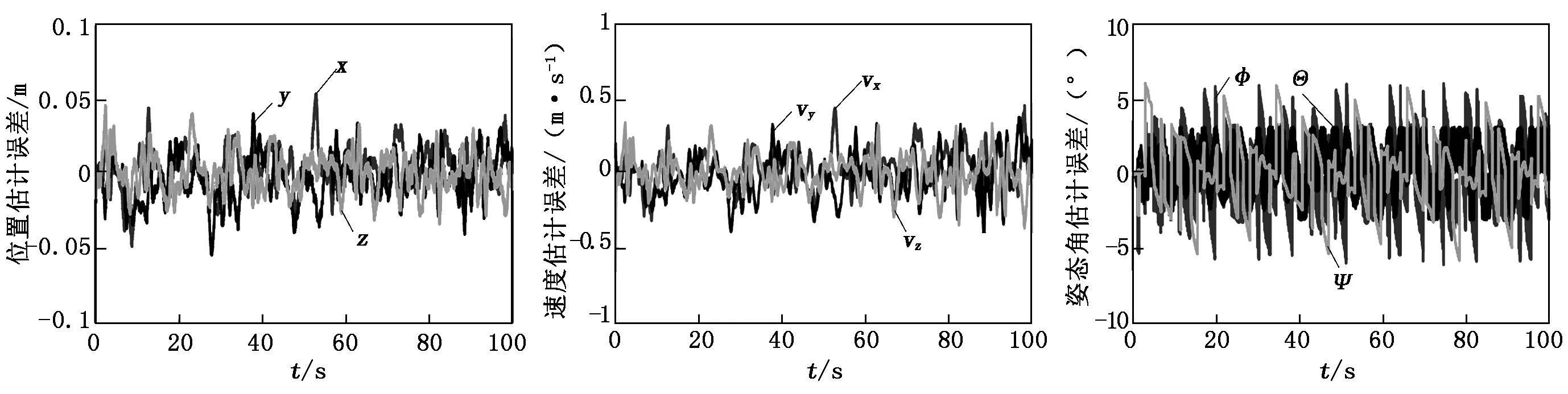
图2 位置估计误差 图3 速度估计误差 图4 姿态角估计误差

4 结束语

本文对四旋翼飞行器的位姿估计算法进行了研究，采用几何扩展卡尔曼滤波算法实现了惯性导航系统和GPS系统的信息融合。通过将旋转矩阵误差向量和经一致性表示的惯性传感器漂移误差作为状态误差矢量，推导出了基于一致性表示的扩展卡尔曼滤波。仿真结果表明所提出的算法能较好地实现四旋翼飞行器的位姿估计。