内置式永磁同步电机气隙磁密与漏磁解析计算*

张明强，于慎波，翟凤晨，窦汝桐

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引言

永磁同步电机因具有转矩密度高、恒功率范围宽和制造成本低等优点，其应用范围越来越广泛。然而，在一些国防等特殊应用场合，其振动和噪声问题急待解决。永磁同步电机电磁振动噪声占主导地位[1]，而作用在定子上的径向电磁力是产生电磁振动噪声的主要原因。因此，计算径向气隙磁密是分析振动噪声的核心问题[2]。文献[3]采用等效磁网络法对表贴式电机进行了建模分析，考虑了定子齿部的影响，计算出了漏磁系数与磁通量，但是没有计算出气隙磁密。文献[4]提出了一种新型横向磁通永磁电机的动态等效磁网络模型，解析计算得到了电机的空载反电势和电感波形，但是没有对气隙磁密进行深入研究。文献[5]采用等效磁网络法对内置电机进行建模，考虑定子开槽、磁饱和效应的影响，提出了永磁转矩、磁阻转矩的解析方法,但建立的气隙磁密模型精确度不高。文献[6]提出了一种用于内置式永磁同步电机的增强型磁导网络模型，能够计算气隙磁通量、电感、反电动势和电磁转矩。文献[7]采用标量磁位法对组合磁极结构的永磁电机中的气隙磁场进行了解析计算，提出了采用改进的卡特系数对气隙长度进行等效，但是该方法提出的卡特系数没有计算出槽内的磁路长度。

本文提出一种用于转子具有隔磁桥的内置式永磁同步电机的改进等效磁网络模型，考虑到转子隔磁桥对转子磁路和定子磁路的影响，针对齿槽效应进一步优化了相对气隙磁导函数，对各磁路磁通、漏磁系数与气隙磁密进行解析计算，最后通过与有限元法计算结果进行对比，证明了该方法的准确性。

1 内置式永磁同步电机等效磁网络模型建立

1.1 电机结构与磁路分析

本文基于四极六槽永磁同步电机进行解析建模，电机为内置式且转子具有隔磁桥，需考虑其特殊结构对磁路的影响,电机结构如图1所示。

图1 内置式永磁同步电机结构示意图

1.2 等效磁网络模型建立

由于永磁同步电机的对称性，只需要对四分之一电机进行建模即可，该电机的磁路结构如图2所示。磁路1为永磁体产生的主磁通，磁路2和3均为漏磁通。

图2 电机磁路示意图

为简化解析过程做如下假设：①定、转子结构中不存在磁路饱和现象：②定子绕组中电枢电流产生的磁场强度可忽略。

根据图2所示的磁路分布规律，依据磁路的等效欧姆定律，建立了等效磁网络模型，如图3所示。图3中，Φg为气隙主磁通，Φm为永磁体向外磁路提供的总磁通，Φr为永磁体虚拟内禀磁通，Rg为气隙磁阻，Rs为定子磁阻，Rr为转子磁阻，Rmm为相邻永磁体磁路等效磁阻，Rmr为永磁体端部磁路等效磁阻，Rmo为永磁体磁阻。

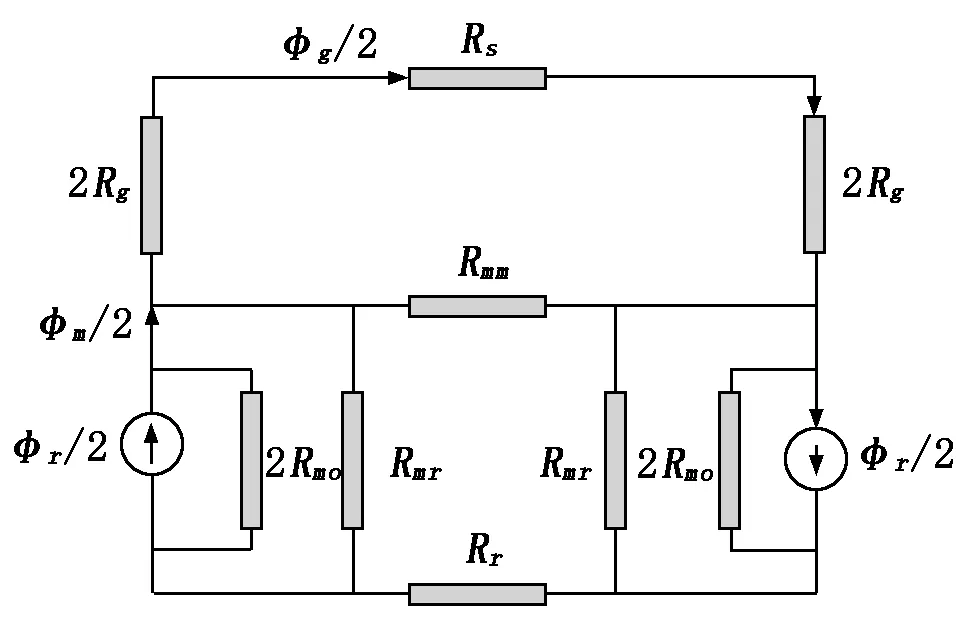
图3 等效磁网络模型

根据前面的假设，不存在磁路饱和现象，所以Rs和Rr相对于Rg的值可以忽略，则将图3简化为图4。

图4 简化等效磁网络模型

2 等效磁阻计算

2.1 气隙磁阻及永磁体磁阻计算

不考虑定子开槽对气隙磁阻造成的影响时，永磁体磁阻为：

(1)

其中：hpm为永磁体厚度；μ0为真空磁导率；μm为永磁体相对磁导率；Am为永磁体磁通通过面积，Am=lwm，l为永磁体轴向长度，wm为永磁体宽度。

气隙磁阻Rg为：

(2)

2.2 相邻永磁体磁路等效磁阻及永磁体端部磁路等效磁阻计算

本文研究了电机隔磁桥的影响，计算磁路2与磁路3磁阻时需要考虑因隔磁桥导致的磁路变化引起的磁阻变化。根据图2的磁路以及磁力线流通路径可以将磁路2等效为两段矩形磁通管路径加一段环形磁通管路径，将磁路3等效为梯形磁通管路径，两磁路等效结构如图5所示。

图5 磁路2与磁路3等效结构

按照磁通路径思想可以得到矩形与环形组合磁路等效磁阻表达式，磁路2磁阻模型如图6所示，磁路3磁阻模型如图7所示。磁路2磁阻为：

(3)

其中：Wg为等效矩形高度；hg为等效矩形长度；rn为等效环形磁路内圆半径；θg为等效环形圆心角；μr为转子铁芯材料的相对磁导率。

磁路3磁阻为：

(4)

其中：Wt为梯形磁路下底边长;Wc为梯形磁路上底边长；hb为梯形磁路高。

图6 磁路2磁阻模型 图7 磁路3磁阻模型

3 气隙磁密解析计算

根据前文所做简化等效磁网络模型，依据磁网络理论，不考虑开槽效应时电机的磁密分布情况如图8所示[8]，利用前文所求得的各项磁阻进行气隙磁场解析。图8中，a为气隙磁密为零的角度，b为气隙磁密从零到达峰值的角度，Baverage为平均磁通密度。

图8 等效无槽气隙磁密分布情况

a、b的计算公式如下：

(5)

(6)

其中：W0为定子槽宽；θp永磁体内端圆心角；Φl为隔磁桥顶部漏磁通量，Φl=BsAl，Bs为定子铁心饱和时的磁通密度，Al为漏磁磁通面积；Φr为永磁体虚拟内禀磁通，Φr=BrAm，Br为剩磁系数。

3.1 磁通与磁通密度计算

根据图4的简化等效磁网络模型可对磁路的总磁阻Rm进行计算：

(7)

(8)

永磁体向外提供的总磁通Φm与气隙主磁通Φg分别为：

(9)

(10)

电机的永磁体内磁通密度Bm与平均气隙磁通密度Baverage为：

(11)

(12)

则漏磁系数为：

(13)

3.2 考虑定子开槽气隙磁密解析计算

在实际计算气隙磁密时，需要考虑到定子开槽导致的气隙磁阻不统一，磁力线总是流过磁阻最小的路径，这些槽会导致电机的气隙磁密波形产生一定程度的形变。引入卡特系数ε，考虑定子开槽效应时的气隙磁密Bslotting为：

Bslotting=εBaverage.

(14)

(15)

其中：gk(θ)为实际磁力线长度，gk(θ)=ge+gc(θ)，gc(θ)为定子开槽导致的随转子角度θ变化的磁力线长度函数。

因为相对定子齿来说定子齿侧面磁力线分布很少，故只考虑齿尖部分磁力线集中的位置，为简化计算只对定子齿、槽的一半建立模型，磁力线分布情况如图9所示。

图9 定子槽磁力线分布情况

定子开槽导致的随转子角度变化的磁力线长度函数gc(θ)与齿尖倾斜角度β可按如下公式计算：

(16)

其中：θ1、θ2、θ3为各磁力线对应的角度；rd为定子半径。

(17)

其中：W1为定子齿距；h1为定子齿尖高度。

4 解析计算与有限元仿真对比验证

利用Ansoft软件建立有限元模型，电机定子外径为107 mm，转子外径为54 mm，电机转速n=3 600 r/min，额定转矩Tn=1.94 N·m，最佳功角为96°，线圈匝数为95，永磁体采用平行充磁，剩磁Br=1.23 T。对四极六槽内置式永磁同步电机进行空载运行下的气隙磁密仿真分析，得到的磁力线分布如图10所示。

图10 永磁同步电机磁力线分布

等效磁网络与有限元计算的各磁路磁通和漏磁系数对比如表1所示。

表1 等效磁网络与有限元计算结果对比

图11为运用改进等效磁网络法与有限元法对一个周期内径向气隙磁密进行求解的对比。改进等效磁网络法与有限元法得到的径向气隙磁密波形吻合度较高，证明了对于开隔磁桥的内置式永磁同步电机利用等效磁网络法进行径向气隙磁密解析建模的可行性。

图11 用等效磁网络法与有限元法得到的径向气隙磁密对比

5 结论

本文针对一台四极六槽转子具有隔磁桥的内置式永磁同步电机，运用改进等效磁网络法分别对各磁路磁通、漏磁系数和气隙磁密进行了计算，并运用有限元法对其进行了验证。

(1) 针对定子开槽造成的气隙磁阻变化，通过对不同磁通路径计算，得出了相对气隙磁导函数，进而求出了考虑定子槽效应的磁导函数。

(2) 应用改进等效磁网络法，分别计算了各磁路磁阻与漏磁系数，并与采用有限元法得到的结果进行了对比，总体误差较小。

(3) 通过建立改进等效磁网络模型，成功求得电机一个周期内的径向气隙磁密，为转子开隔磁桥的内置式永磁同步电机空载气隙磁场研究提供了一种方法。