磁致伸缩效应对永磁同步电机振动噪声影响分析*
2022-10-28于慎波窦汝桐翟凤晨
罗 进,于慎波,窦汝桐,翟凤晨
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
0 引言
电机的振动噪声是电机研究中的主要问题之一,但人们常常忽略铁心磁致伸缩效应的影响[1,2],近些年来国内外学者逐渐重视铁心磁致伸缩效应对电机振动噪声影响的研究。美国学者Mohammed O A等[3,4]提出了一个考虑磁致伸缩效应的电磁、机械力以及相关材料的数值模型,发现铁心磁致伸缩效应也会引起定子形变,在计算时发现铁心磁致伸缩效应对一台2马力电机的影响达到了50%。英国帝国理工大学博士Belahcen Anouar[5]分别计算了一台同步电机和一台异步电机定子铁心的振动,发现在某些频率铁心磁致伸缩效应会加剧定子铁心振动,而在另外一些频率会使其减小。沈阳工业大学的韩雪岩等[6]利用有限元法对有铁心磁致伸缩效应的电机伸缩进行数值计算,分析了电机的振动噪声。河北工业大学的闫荣格等[7]对实际工况下考虑电磁力和磁致伸缩效应的感应电机的应力和振动进行计算,并分析了谐波对电机振动的影响。本文对永磁同步电机进行建模和仿真分析,以确定铁心磁致伸缩效应对永磁同步电机振动噪声的影响。
1 电机的机电耦合数学模型
根据麦克斯韦方程和材料的各向异性的描述,得到激励电流z方向分量Je的偏微分方程:
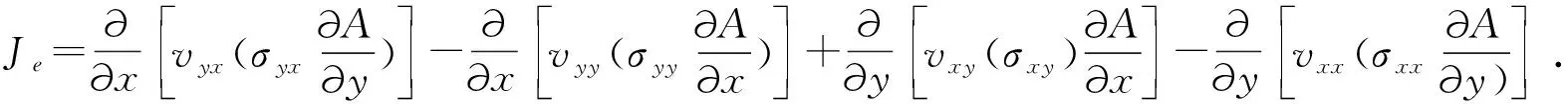
(1)
其中:vxx、vxy、vyx、vyy为平面内不同方向的磁阻率对单元应力的变化率;σxx、σxy、σyx、σyy为应力张量在不同方向的值;A为磁矢势。
电机系统的总能量泛函Et可以用式(2)来表示,该系统包括磁场能、电流位能、机械能和外力做功大小。

(2)
其中:R为磁场域;B为磁通密度;H为磁场强度;V为机械域的体积;ε、σ为应变张量和应力张量;fV为外部体积力密度;τ为机械域边界;fτ为外部表面力密度;U为振动位移。
将机械系统总能量分别对振动位移和磁矢势求偏导,可得到机械场和磁场的能量泛函驻点如式(3)、式(4)所示:

(3)
(4)
其中:Etm为机械场总能量;Ete为磁场的总能量;Ui和Ai分别为机械场和磁场在节点i处的位移和磁矢势。
根据虚功原理,通过保持两个节点之间磁矢势之差不变,则沿位移方向的电磁作用力等于磁能相对位移的变化。每个单元电磁力可以表示为:

(5)
其中:Re为单元电磁场的面积;G为雅可比微分矩阵。
式(5)中第三项相当于磁致伸缩力的分量,而且在式(5)中可以得到:
(6)
其中:E为材料的弹性模量;v为泊松比。所以磁致伸缩单元力可以用式(7)表示:
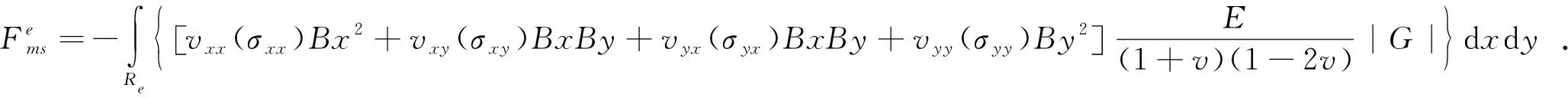
(7)
可以得到如下用来表示电磁场和机械场耦合问题的矩阵:
[S][A]=[Je].
(8)
[K][U]=[F].
(9)
其中:[S]为电磁刚度矩阵;[A]为磁矢量矩阵;[Je]为激励电流密度矩阵;[K]为机械刚度矩阵;[U]为振动位移矩阵;[F]为施加在应力场中的力,包括电磁力和磁致伸缩力。
2 电机电磁场仿真分析
本文以一台9.5 kW8级36槽的永磁同步电机为研究对象,利用Maxwell建立的电机二维有限元仿真模型如图1所示。电机在工作过程中的主要参数如表1所示。本文电机硅钢片的磁致伸缩特性曲线如图2所示。将曲线数值添加到硅钢片的材料属性中,计算有磁致伸缩效应时的径向电磁力。
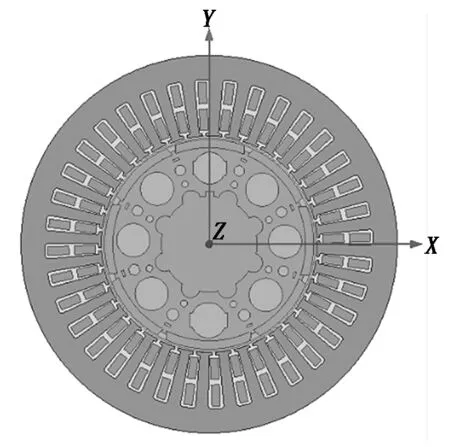
图1 电机有限元计算模型

表1 电机主要参数
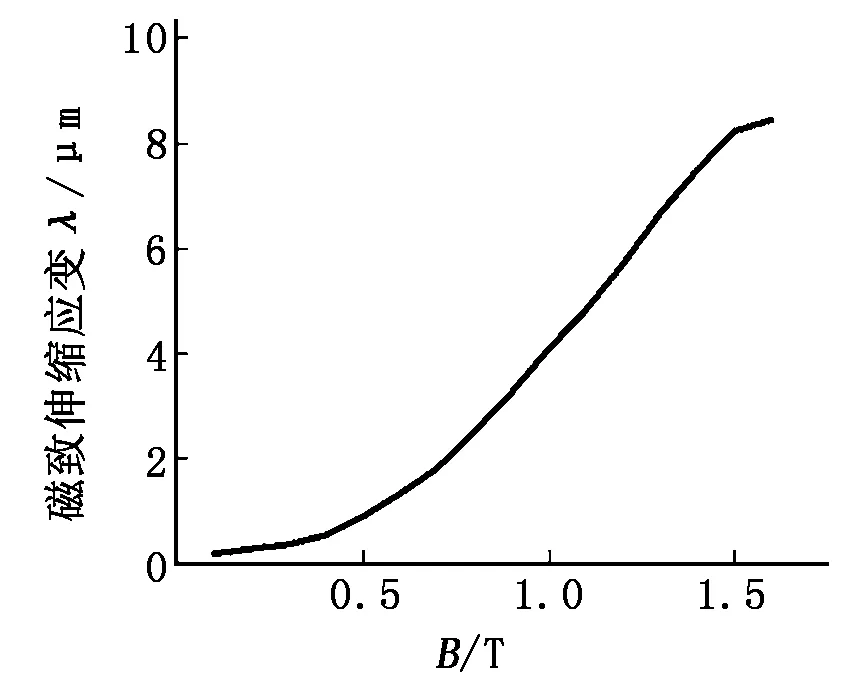
图2 电机硅钢片的磁致伸缩特性曲线
图3为有磁致伸缩效应和无磁致伸缩效应时的径向电磁力与谐波分析对比,取半个电周期结果进行观察。从图3(a)中可以看出,在数值上有磁致伸缩效应的电磁力总体比无磁致伸缩效应的大。从图3(b)中可以看出,电磁力低次谐波的幅值较大,可能会引起较大的振动,但当电磁力特定阶次激振力波频率与电机固有频率接近时,力波的幅值较小也会发生共振。

图3 有、无磁致伸缩效应时的径向电磁力与谐波分析对比
3 电机模态与谐响应仿真分析
利用ANSYS Workbench建立电机的三维模型,已知电机材料,其泊松比为0.28,弹性模量为196 GPa,密度为7 700 kg/m3。利用模态计算模块进行分析,得到的电机前6阶模态固有频率如表2所示。

表2 电机前6阶模态固有频率
图4为有、无磁致伸缩效应电机机壳表面的加速度频谱对比图。为了方便观察,将振动加速度取对数即为振动加速度级。由图4可以看出,振动加速度最大的频段在6 400 Hz,之后下降。原因是此频段接近第6阶模态的固有频率。电机第6阶模态的振型如图 5所示。

图4 有、无磁致伸缩效应时电机机壳表面加速度级
4 电机噪声仿真分析
在电机外建立半径1.5 m的空气包作为声场响应计算区域,得出有、无磁致伸缩效应时机壳表面的声压级曲线,如图6所示,发现有磁致伸缩效应时的噪声在大部分情况下大于无磁致伸缩效应的。
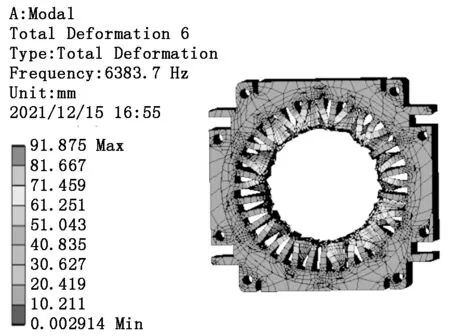
图5 电机第6阶模态振型
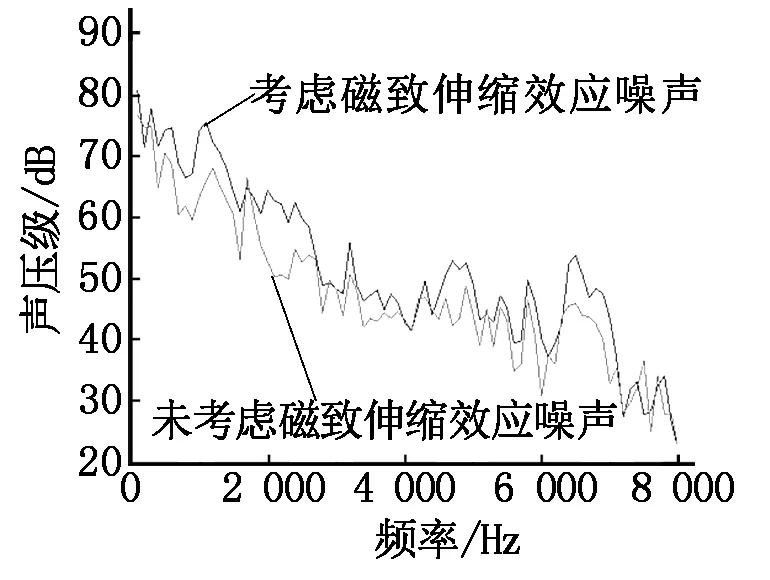
图6 有、无磁致伸缩效应时机壳表面的声压级曲线
5 结论
本文分别建立了永磁同步电机的二维和三维有限元模型,并进行电磁场计算、模态和固有频率分析、振动噪声分析。对有无磁致伸缩效应的径向电磁力、振动加速度和噪声进行分析,可以得到有磁致伸缩效应的各项结果均比无磁致伸缩效应的大,研究结果对电机的减振降噪以及设计制造有一定的指导意义。
