前峰型降雨入渗过程双层地基基质吸力解析解*

徐瑞麟，秦卫星,,3，何 勇，胡惠仁，阳 乐，王 聪，熊轩宇

(1.长沙理工大学国际工学院，湖南 长沙 410114;2.长沙理工大学水利与环境工程学院，湖南 长沙 410114；3.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114;4.长沙理工大学交通运输工程学院，湖南 长沙 410114)

雨水入渗会增加地基中上部土体含水量，减小地基土体基质吸力，降低地基承载性能，给工程安全造成不利影响[1-4].因此，快速准确预测降雨入渗作用下地基基质吸力演化特性，对雨季地基承载性能评价和地基防灾减灾具有重大现实意义.因简单、直观、高效等优点，解析法一直是国内外研究雨水入渗作用下非饱和土基质吸力演化的主要手段.

Srivastava等[5]率先基于Richards一维非饱和渗流控制方程，引入Gardner土-水特征曲线模型，利用拉普拉斯变换，求得了等雨强入渗作用下均质和双层地基的瞬态渗流解析解.吴礼舟等[6]推导了渗流变形耦合作用下均质土层和双层土基质吸力解析解，分析了均匀型降雨入渗过程地基基质吸力的演化特性.李宁等[7]利用傅里叶变换分别推导了恒定雨强小于和大于土体饱和渗透系数时无限长斜坡的基质吸力解析解，并给出了两种情况下斜坡基质吸力解析解的统一表达式.Zhan等[8]基于二维非饱和渗流控制方程，采用描述土体土水特征和渗透系数的指数模型，获得了降雨入渗条件下无限长边坡的基质吸力解析解，并将其用于研究降雨入渗对非饱和土斜坡稳定性的影响.邱清文等[9]基于非饱和渗流控制方程，采用单位梯度边界作为土质覆盖层的底部边界条件，推导了可考虑任意初始条件的基质吸力解析解.此外，众多学者基于Richards瞬态非饱和渗流方程，先后得到了前峰型、中峰型、后峰型降雨过程均质地基基质吸力瞬态解析解[10-12].由此可见，目前非饱和土体降雨入渗解析解研究已取得较丰硕成果，但多假定雨水以恒定均匀雨强入渗，仅有少部分针对均匀土的研究考虑了非均匀雨强入渗的影响，非均匀型降雨作用下双层地基基质吸力解析解尚未见报道.

为此，本研究以双层非饱和地基为研究对象，以前峰型降雨为例开展了非均匀型降雨入渗过程双层地基基质吸力瞬态解析解研究.首先，笔者建立了前峰型降雨入渗作用下双层地基水分运移概化模型，引入Gardner土-水特征函数[13]，化简Richards非饱和渗流控制方程，利用拉普拉斯变换推导了前峰型降雨入渗过程双层地基基质吸力瞬态解析解.其次，笔者通过算例分析，对比了有限单元法模拟与解析解的结果，证明了解析解是正确的，该解析解可为研究非均匀型降雨入渗作用下地基基质吸力演化特性提供便捷手段.

1 前峰型降雨入渗作用下双层地基水分运移模型

1.1 双层地基雨水入渗概化模型

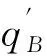
(1)

基于上述假定，绘制双层非饱和地基降雨入渗概化模型(图1).

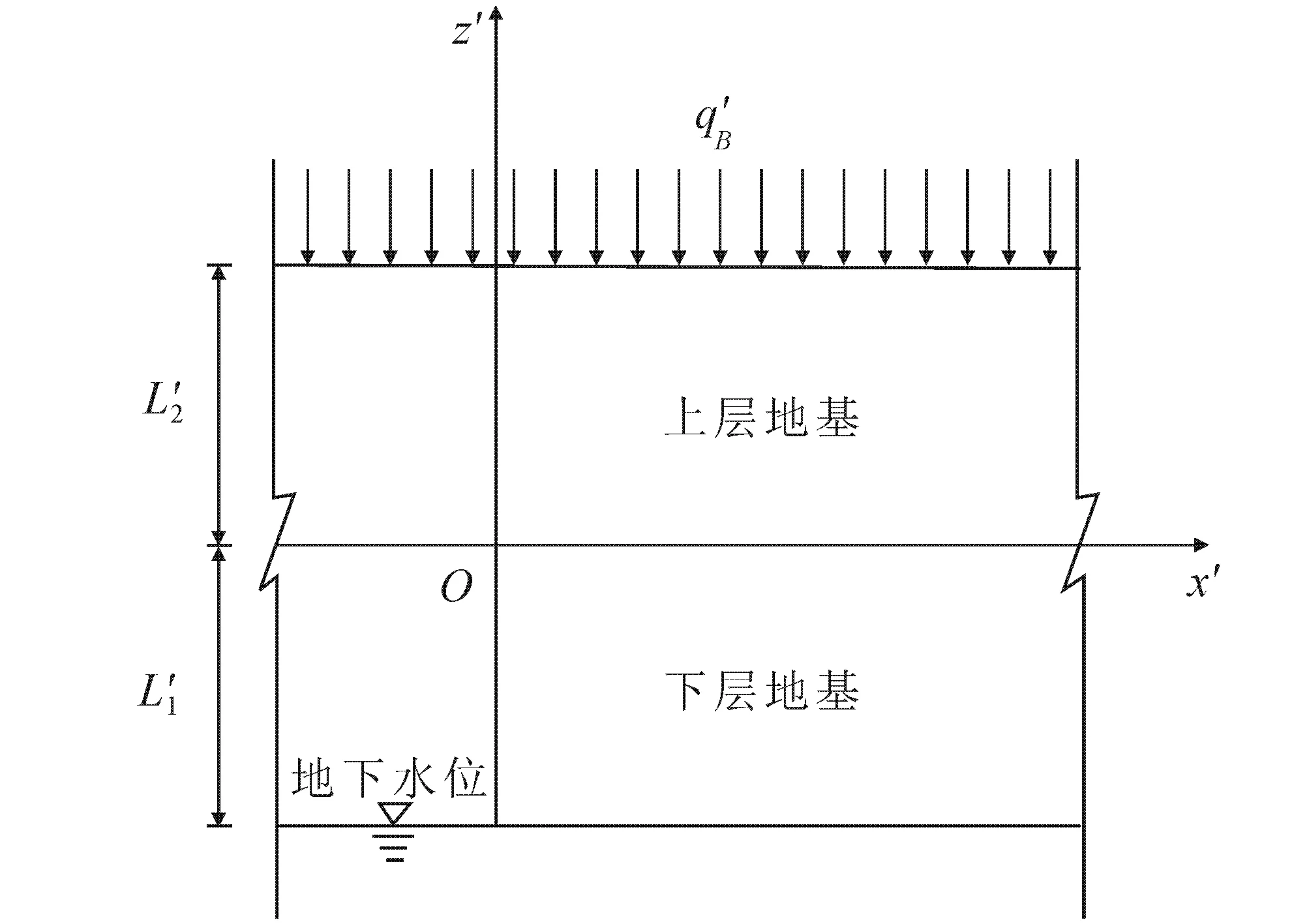
图1 双层地基降雨入渗概化模型Fig. 1 Schematic Model of Rainfall Infiltration into Two-Layered Foundation

1.2 控制方程

建立图1所示双层地基遭遇前峰型降雨铅直入渗的Richards非饱和渗流控制方程：

(2)

其中：K′为非饱和土体渗透系数，cm/h；ψ为降雨历时t′后z′处的基质吸力，cm；θ为体积含水量，cm3/cm3.

为解决非饱和土基质吸力与非饱和渗透系数高度非线性关系给式(2)解析解推导造成的困难，参照文献[4-5]引入式(3)、(4)所示Gardner土-水特征函数来描述含水量、非饱和渗透系数、基质吸力三者之间的关系.

K′=Kseαψ，

(3)

θ=θr+(θs-θr)eαψ.

(4)

其中：Ks为饱和渗透系数，cm/h；α为去饱和系数，cm-1；θr为残余体积含水量，cm3/cm3；θs为饱和体积含水量，cm3/cm3；其他参数意义与前文一致.

将式(3)、(4)代入式(2)，可得

(5)

(6a)

(6b)

(6c)

(6d)

(6e)

(6f)

结合式(5)与式(6a)～(6f)，两层地基的渗流控制方程可简化为：

(7a)

(7b)

1.3 初始条件

K1(z,0)=qA1-(qA1-eα1ψ0)e-(L1+z)=K10(z)，

(8a)

(8b)

1.4 边界条件

根据基本假定2，可知双层地基下边界条件为恒定孔隙水压力，

[K1]z=-L1=eα1ψ0,

(9)

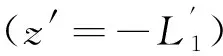
根据基本假定3，可知双层地基上边界条件为流量边界，

(10)

在降雨入渗任意时刻，上、下层接触面流量、基质吸力相等，

(11)

(12)

2 控制方程求解

利用拉普拉斯正、逆变换，结合初始条件和边界条件对非饱和渗流控制方程(7a)，(7b)进行求解.

2.1 拉普拉斯正变换

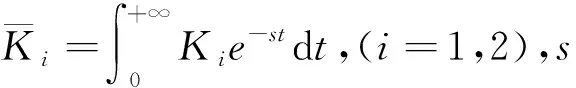
(13a)

(13b)

同理，式(9)～(12)所示边界条件可变换为

(14)

(15)

(16)

(17)

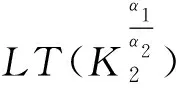
为方便解析解推导，采用文献[5-6]类似的做法，假定两层土体去饱和系数α1=α2，联立式(14)～(17)，可得偏微分方程组(13a)、(13b)的解析解为

(18a)

(18b)

其中：

上式中：

Ds1=s{-[sinh (pL1)+2pcosh (pL1)]·[sinh (qL2)+2pcosh (qL2)]+

Ds2=s2{-[sinh (pL1)+2pcosh (pL1)]·[sinh (qL2)+2pcosh (qL2)]+

2.2 拉普拉斯逆变换

运用留数定理对式(18a)、(18b)进行拉普拉斯逆变换，得到前峰型雨水入渗过程双层地基渗透系数表达式：

(19a)

(19b)

其中：X1、X2、XA1、XA2、XB1、XB2、XC1、XC2、Y1、Y2、YA1、YA2、YB1、YB2、YC1、YC2均为z和t的函数.

X1=-0.5sinh [0.5(L1+z)]·{[sinh (0.5L1)+cosh (0.5L1)]·

[sinh (0.5L2)+cosh (0.5L2)]}-1，

(20a)

(20b)

(21a)

(21b)

其中

Dn表述式中：

λn的特征方程为

[sin (λL1)+2λcos(λL1)][sin (μL2)+2μcos(μL2)]-

(22)

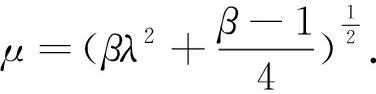
当β>1时，

(23a)

(23b)

其中

Dn表述式中：

λn的特征方程为

(24)

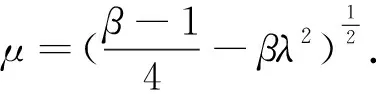
当β<1时，

(25a)

(25b)

其中

Dn表述式中：

λn的特征方程为

(26)

(27a)

(27b)

其中：

As1=0.5tsinh (0.5(L1+z))+βsinh (0.5(L1+z))+0.5(L1+z)cosh (0.5(L1+z))；

Ds=-[sinh (0.5L1)+cosh (0.5L1)]·[sinh (0.5L2)+cosh (0.5L2)];

Ds1=-(L1+βL2)sinh (0.5L1)sinh (0.5L2)-(2β+L1+βL2)sinh (0.5L1)cosh (0.5L2)-(2+

L1+βL2)cosh (0.5L1)sinh (0.5L2)-[2(β+1)+L1+βL2]cosh (0.5L1)cosh (0.5L2)；

(28a)

(28b)

λn的特征方程为

(29)

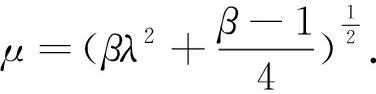
当β>1时，

(30a)

(30b)

λn的特征方程为

(31)

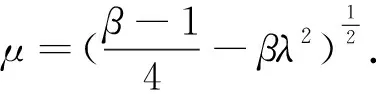
当β<1时，

(32a)

(32b)

λn的特征方程为

(33)

通过式(20a)、(20b)获得前峰型雨水入渗过程双层地基渗透系数瞬态解后，就可根据式(3)、 (6c)、(6e)得到上、下层地基沿深度分布的基质吸力瞬态解析解：

(34a)

(34b)

3 解析解考证

以某双层非饱和地基为研究对象，地下水位距离地表5 m，上、下两层地基土体厚度均为2.5 m.地基土体物理力学参数如下：下层地基土体饱和渗透系数Ks1为1 cm/h，上层地基饱和渗透系数Ks2为10 cm/h，两层土体去饱和系数α相同，为0.01cm-1，饱和含水量θs相同，为0.4 cm3/cm3，残余含水量θr相同，为0.06 cm3/cm3.该地基前期未遭遇降雨，前期雨强qa取为0 cm/h.后期遭遇历时12 h，总降雨量为60 mm的暴雨，雨型为前峰型，起始雨强q0为0.8 cm/h，雨强变化系数a为-0.05 cm/h2.取长5 m、高5 m范围内的地基，建立如图2所示的有限元数值模型.

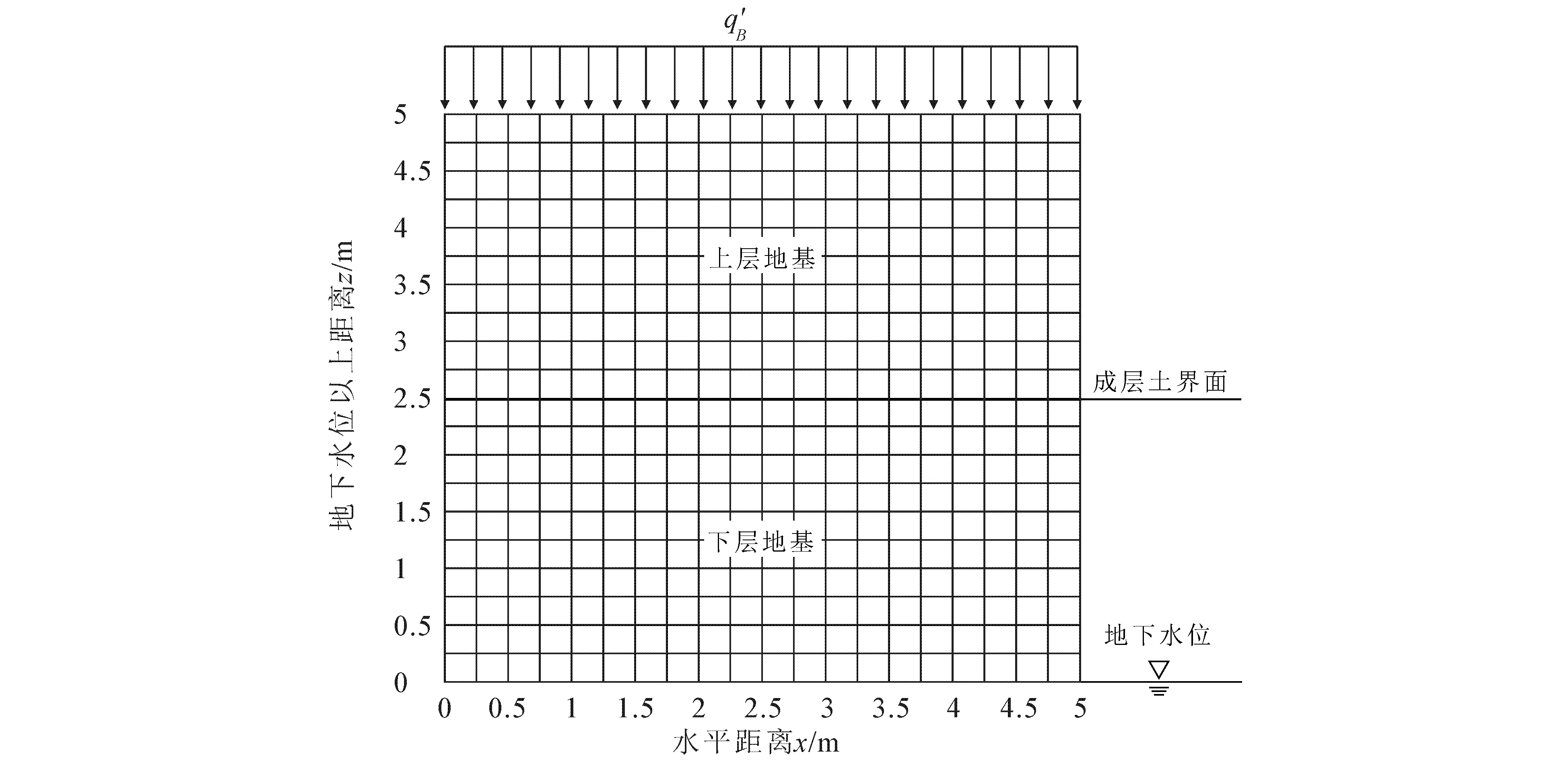
图2 降雨入渗下地基基质吸力计算的有限元模型Fig. 2 Finite Element Model for Calculating the Matrix Suction of Foundation for Rainfall Infiltration

利用Geo-Studio软件的渗流有限元计算模块SEEP/W和前峰型条件下基质吸力解析解表达式计算雨水入渗过程地基沿深度方向的基质吸力,其分布演化规律如图3所示.

图3 前峰型降雨入渗过程地基基质吸力演化Fig. 3 Evolution of Matrix Suction of Two-Layered Foundation for Advanced-Peak Rainfall Infiltration

从图3可以看出，雨水入渗后成层地基基质吸力沿深度分布呈现显著分层非线性特征：(1)靠近地基表面附近的土体基质吸力随雨水入渗先迅速减小，在降雨4.2 h后地基表面基质吸力达到最小值-289 cm，随后逐渐升高，明显不同于恒定均匀雨强入渗过程地基基质吸力一直减小的特点[5]；(2)上层地基土体基质吸力随着降雨历时增加而不断减小，呈现先快后慢特点；(3)下层地基基质吸力减小速度明显滞后于上层地基，基质吸力分布的深度随降雨历时推移而不断增加.同时，可以看出数值模拟结果和解析解的大小和变化规律几乎一致，表明推求的前峰型降雨入渗作用下双层地基基质吸力解析解是正确的.

4 结论

基于Richards瞬态非饱和渗流方程，笔者引入Gardner土-水特征函数，建立了前峰型降雨入渗作用下双层非饱和地基水分运移模型，利用拉普拉斯变换推导了前峰型降雨过程双层地基基质吸力瞬态解析解，并用有限元模拟结果证明了其正确性.算例结果表明，降雨开始后靠近地基表面附近的土体基质吸力随雨水入渗先迅速减小，在降雨4.2 h后地基表面基质吸力达到最小值-289 cm，随后逐渐升高；上层地基土体基质吸力随着降雨历时增加而不断减小，呈现先快后慢特点；下层地基基质吸力减小速度明显滞后于上层地基，基质吸力分布的深度随降雨历时推移而不断增加.本研究获得的解析解为快速预测非均匀型降雨入渗作用下双层地基基质吸力演化特性提供了便捷手段，可为雨季地基承载性能评价和防灾减灾提供技术支持.