基于三轴试验生态袋加筋土邓肯-张模型参数研究

蒋希雁，许梦然，陈宇宏

（1.河北建筑工程学院，河北张家口 075031；2.河北省土木工程诊断、改造与抗灾重点实验室，河北张家口 075031；3.河北省寒冷地区交通基础设施工程技术创新中心，河北张家口 075031）

0 引言

边坡的破坏形式主要表现为：崩塌、剥落、滑坡和坍塌，尤其是在暴雨过后，边坡土体的含水率剧增，导致土体工程性质变差，出现边坡失稳现象，对人们的安全和国家财产造成极大的影响［1-3］，因此开展含水率对边坡土体力学性质影响的研究有利于解决因含水率变化所带来的边坡工程问题。

已有的文献表明［4-6］，含水率的变化对土体的力学性质都有着显著的影响。薛振声等［7］对不同含水率的新近系粉质黏土进行三轴试验，发现粉质黏土的峰值强度受含水率影响较大，且黏聚力的对数值、内摩擦角均随着含水率的增加呈负线性关系。欧湘萍等［8］对黄土进行三轴固结不排水试验，研究发现黄土的内摩擦角与含水率的相关性远低于黏聚力与含水率的相关性。颜阳等［9］对不同含水率的煤系土进行三轴固结排水试验，并计算得到各含水率下试样的邓肯-张模型参数，发现含水率对煤系土邓肯-张模型参数影响程度均有所不同，其中黏聚力受含水率影响最为显著，参数n值和破坏比随含水率的增加而增大，黏聚力、初始切线模量和K值均随含水率的增加而减小。周春梅等［10］对三门峡地区黄土进行不固结不排水三轴试验，试验结果表明，随着含水量的增加，黄土试样的应力-应变关系曲线由弱应变硬化向强应变硬化转变；黏聚力与含水率的变化呈明显负线性相关，内摩擦角与含水率无明显的相关性。毛海涛等［11］对三峡库区紫色土进行三轴固结不排水试验，发现紫色土黏聚力随着含水率的增加呈现出先增加后减小的趋势，在含水率为12%时，黏聚力存在峰值，而内摩擦角随含水率的增加呈线性减小。罗崇亮等［12］对不同含水率的红层泥岩土进行三轴试验，研究发现试样的黏聚力和内摩察角均与含水率呈负线性关系，含水率对内摩擦角的影响较为显著；不同含水率下邓肯-张模型参数破坏比在一定范围内波动，K值随含水率增大而减小呈负线性关系，n值随含水率的增大而增大呈线性关系。

由上述研究可以看出，对于不同种类土体，含水率对其力学特性和本构模型参数均有一定影响。而目前关于生态袋护坡的研究，多数集中在生态袋护坡的施工技术研究和应用效果分析［13-15］，生态袋加筋土作为生态袋护坡的护坡体，含水率对生态袋加筋土力学特性和本构模型参数影响的研究较为缺乏。鉴此，本文以生态袋加筋土为研究对象，在不同的含水率条件下进行三轴不固结不排水试验，研究含水率对生态袋加筋土邓肯-张模型参数的影响，提出受含水率影响的模型参数经验公式，为生态袋护坡工程的设计和数值模拟提供一定的理论依据和参数支持。

1 试验材料及方法

1.1 试验材料

试验土样为粉质黏土，土样物理性质指标如表1 所示。加筋材料为仪征康顺土工材料有限公司所生产的生态袋，其相关参数如表2所示。

表2 生态袋基本性能参数Tab.2 Basic performance parameters of ecological bag

1.2 试验方法

试样制备：本文试样制备参照《土工试验方法标准》［16］。先将所取试验用土在105 ℃的烘箱中放置12 h，烘干后碾碎过5 mm 的筛，分别配置含水率为8%、10%、12%、14%的4 组试样用土。为保证水分与土体充分均匀混合，用塑料袋密封24 h 后再进行制样过程。将每组试验用土分5 层进行击实，制成压实度为85%，直径为61.8 mm，高125 mm 的圆柱体试样，将制作完成后的试样用生态袋包裹四周并缝制，缝制后的试样如图1所示。

图1 缝制后的试样Fig.1 Sample after sewing

三轴试验：试验仪器采用南京土壤仪器厂所生产的全自动流变三轴仪01-LH0501，如图2 所示。对生态袋加筋土试样进行三轴不固结不排水试验，围压分别取50、100、150和200 kPa，试验剪切速率取0.8%/min。

图2 全自动流变三轴仪Fig.2 Fully automatic rheological triaxial apparatus

试验终止条件及破坏点的确定：依据《土工试验方法标准》［16］，当生态袋加筋土的应力-应变关系曲线出现峰值时，试验进行至峰值后的3%～5%轴向应变；应力-应变关系曲线无峰值时，则试验剪切至轴向应变的20%。本研究中生态袋加筋土的应力-应变关系曲线均无峰值点，故选取轴向应变（ε1=15%）相应的偏应力点作为破坏点。

2 试验结果整理与分析

2.1 应力-应变曲线关系

同一围压下，不同含水率生态袋加筋土的应力-应变关系曲线如图3 所示。由图3 可知：生态袋加筋土试样轴向应变在约小于2%时，应力随应变增加大致呈线性增长，试样处于弹性变形阶段；在约大于2%后，随轴向应变增加，偏应力的增长速率减慢，应力-应变关系曲线呈非线性增长，此时试样发生塑性变形；随着含水率的增加，生态袋加筋土的偏应力逐渐减小。

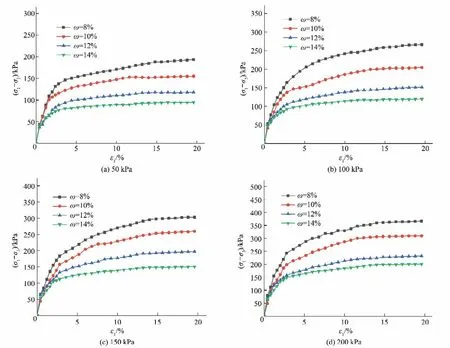
图3 不同含水率下生态袋加筋土的应力-应变曲线Fig.3 Stress-strain curves of eco bag reinforced soil under different moisture content

同一含水率下，不同围压生态袋加筋土的应力-应变关系曲线如图4 所示，由图4 可以看出：随着围压的增加，生态袋加筋土的偏应力均不断增大。生态袋加筋土在试验过程中，应力-应变关系曲线均未出现峰值点，表现为应变硬化型。对图4中生态袋加筋土应力-应变关系曲线进行双曲线拟合，拟合相关系数均大于0.97，这说明生态袋加筋土的应力-应变关系呈现出双曲线特征。

图4 不同围压下生态袋加筋土的应力-应变曲线Fig.4 Stress-strain curves of eco-bag reinforced soil under different confining pressures

2.2 破坏强度

生态袋加筋土的应力-应变关系均为应变硬化型，选取轴向应变为15%时的主应力差为破坏应力即破坏强度。表3为试样在不同围压和含水率下破坏强度值，同时，为更加直观地表现出生态袋破坏强度与含水率、围压的关系，绘制含水率、围压与生态袋加筋土破坏强度关系曲面图如图5所示。

表3 不同含水率和围压下试样的破坏强度Tab.3 Failure strength of samples with different moisture content and confining pressure

由图5可以看出：在相同含水率下，试样的破坏强度与围压呈正比关系，即围压越大，试样破坏时所需的偏应力就越大。其原因在于随着围压的增加，试样在压缩过程中所受握裹力增大，侧向变形受到的约束力越大，从而导致试样的土颗粒之间的摩阻力增加，提高了试样的破坏强度。

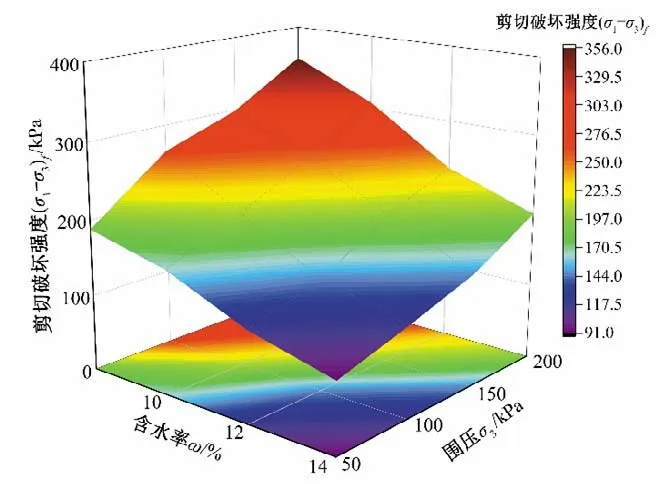
图5 含水率、围压与破坏强度关系Fig.5 Water content-failure strength and confining pressure-failure strength relationship

在相同围压下，试样的破坏强度与含水率呈反比关系，即含水率越高，试样破坏时所需的偏应力就越小。这是由于水在土颗粒与生态袋、土颗粒与土颗粒之间有润滑作用，随着试样的含水率增大，土与袋和土与土之间的润滑作用增大，致使土颗粒与生态袋、土颗粒与土颗粒之间的咬合摩擦力和滑动摩擦力（摩阻力）降低，使试样整体强度降低。

3 邓肯-张模型参数的确定

邓肯-张模型的实质是应用增量法概念逼近非线性应力-应变曲线，能够较好地反映土体的非线性状态，因其概念清晰，易于理解，参数较少且求解方便，在土木水利工程和岩土工程中得到广泛应用［17，18］。通过上述三轴压缩试验得到不同含水率下生态袋加筋土的邓肯-张模型参数，分析含水率对生态袋加筋土邓肯-张模型参数影响规律。

3.1 黏聚力c和内摩擦角ϕ

根据生态袋加筋土的三轴压缩试验结果，在τ-σ应力平面上绘制不同含水率下试样破坏时的摩尔应力圆和强度包线，得到生态袋加筋土的抗剪强度指标。图6 给出含水率为8%时生态袋加筋土的摩尔应力圆及相应的强度包线，用同一方法获得含水率为10%、12%和14%试样的黏聚力和内摩擦角，如表4所示。从表4可以看出：黏聚力c和内摩擦角ϕ均随着含水率的增加而减少。含水率从8%增至14%的过程中，黏聚力由43.3 kPa 降至24.3 kPa，减幅达到43.9%；而内摩擦角由23°降至13°，减幅达到43.5%。由此可见，试样的含水率仅增长了6%，而抗剪强度指标c和ϕ却减小了近一半。试样的抗剪强度指标（黏聚力和内摩擦角）随含水率的增加而减少，原因在于：随着含水率的增加，土颗粒间胶结物的胶结作用减弱，导致试样的黏聚力减少；而随着含水率的增大，土体颗粒之间、土颗粒与生态袋之间的润滑作用增强，导致土颗粒之间及土颗粒与生态袋之间的摩擦力减弱，内摩擦角减小。

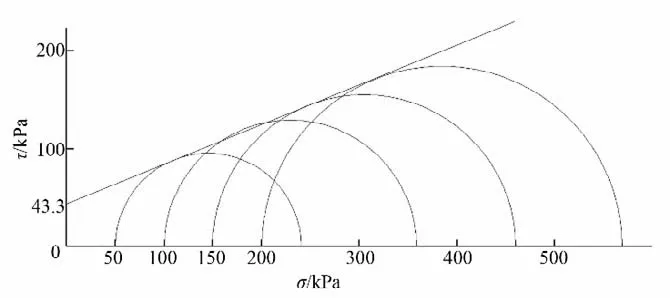
图6 含水率为8%时生态袋加筋土的摩尔应力圆和强度包线Fig.6 Mohr，s stress circle and strength envelope of eco-bag reinforced soil when moisture content is 8%

表4 不同含水率生态袋加筋土的抗剪强度指标Tab.4 Shear strength index of reinforced soil of eco-bag with different moisture content

对黏聚力与含水率及内摩擦角与含水率的关系进行拟合，拟合结果如图7 所示。通过拟合发现：黏聚力和含水率成二次函数关系，相关系数为0.998 8，函数表达式为：

图7 黏聚力、内摩擦角与含水率关系曲线Fig.7 Relationship curve of Cohesion-moisture content and internal friction angle-moisture content

内摩擦角与含水率成线性关系，相关系数为0.994 8，函数表达式为：

3.2 初始切线模量Ei和破坏比Rf值

根据Kondner等［17］的建议，将生态袋加筋土的应力-应变关系用双曲线模型表示为式（3），生态袋加筋土三轴试验结果按-ε1的关系进行处理，如图8 所示，并对其进行线性拟合。

式中：a、b为三轴试验参数，即为图8中拟合直线的截距和斜率。

通过图8 中直线的截距和斜率，可以得到生态袋加筋土在不同围压和含水率下系数a、b的值，其线性拟合的相关系数也汇入表内，如表5所示。

表5 不同含水率下试样a，b取值Tab.5 Sample a，b values under different moisture content

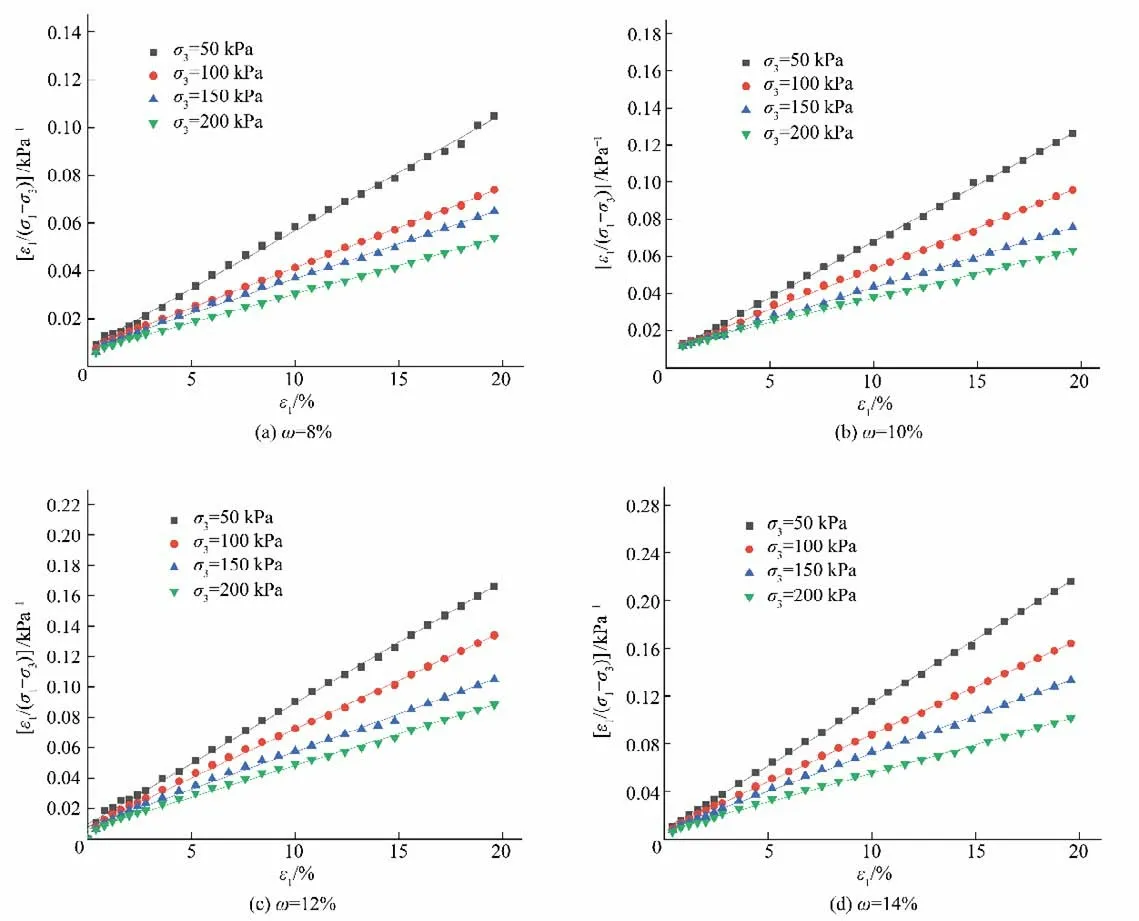
图8 不同含水率试样的-ε1关系曲线Fig.8 -ε1relationship curve of samples with different moisture content

在常规三轴试验中，由于dσ2=dσ3=0，所以其切线模量为：

在式（3）中，当ε1→+∞时，可得式（5）：

在式（4）中，当ε1→0+时，可得式（6）：

即a可看作生态袋加筋土初始剪切模量的倒数，b可看作生态袋加筋土极限偏应力的倒数。

令Rf为生态袋加筋土的破坏应力与主应力差极限值的比值（破坏比［17］），根据莫尔-库仑强度准则确定破坏应力可得：

通过式（6）计算出生态袋加筋土的初始切线模量Ei，如表6所示。由表6 可知：生态袋加筋土的初始切线模量随围压的增大在逐渐增大；而随着含水率的增加，初始切线模量在逐渐减小。

表6 参数Ei的计算Tab.6 Calculation of parameterEi

通过式（7）计算出生态袋加筋土的破坏比Rf，如表7 所示。由表7可知：生态袋加筋土的破坏比Rf变化区间范围为（0.828～0.990）。

表7 参数Rf的计算Tab.7 Calculation of parameterRf

3.3 K、n值

将式（5）、式（6）和式（7）带入式（4）中得：

根据Janbu［18］经验公式，将土体的初始切线模量Ei用围压的函数表示为：

式中：Pa为单位大气压（101.4 kPa）；K、n为试验常数，即分别为双对数坐标下lg（Ei/Pa）-lg（σ3/Pa）直线的截距与斜率。

对不同含水率下生态袋加筋土试样的lg（Ei/Pa）与lg（σ3/Pa）关系曲线进行拟合，拟合结果如图9 所示，直线方程如式（10），拟合相关系数均大于0.96。将直线的截距与斜率汇入表8中。

表8 不同含水率下试样的邓肯-张模型参数Tab.8 Duncan-Chang model parameters of samples under different moisture content

图9 lg（Ei/Pa）与lg（σ3/Pa）关系曲线Fig.9 Relationship curve of lg（Ei/Pa）and lg（σ3/Pa）

对不同含水率下的n值和K值进行拟合，如图10所示，拟合函数表达式如式（11）、式（12），由图10 可知：n值和K值均随着含水率的增大而减小；n值和K值均与含水率成负线性关系。

图10 K、n与含水率的关系Fig.10 The relationship between K-moisture content and n-moisture content

式中：常数项n0为令含水率为0%时的K值，等于0.252 2，相关系数为0.954 6；常数项K0为令含水率为0%时的n值，等于1.762 9，相关系数为0.966 3。

将式（11）、式（12）代入式（9）中，得到以含水率为影响因子的生态袋加筋土初始切线模量公式为：

4 试样尺寸效应分析

在实际工程应用中，生态袋的尺寸远大于三轴试样的尺寸，为了将三轴试验结果用于推算实际生态袋支护结构的安全稳定性分析，选取填充度为85%的生态袋试件进行单轴压缩试验，外包生态袋的三轴试样进行无侧限抗压强度试验，对两种不同尺寸试样的应力-应变关系以及破坏模式进行对比分析。

4.1 生态袋试件单轴压缩试验

4.1.1 试验准备

生态袋试件单轴压缩试验所用袋内土的物理性质指标如表1 所示，生态袋材料性质如表2 所示。选用的生态袋规格为37 cm×35 cm，按式（14）得到生态袋填充度为100%时的体积［19］，再计算出含水率为12%、填充度为85%条件下生态袋填充所需土的质量为15.275 kg，并对其进行装填。

式中：L，B分别为生态袋的长度与宽度，cm；V为填充度为100%时生态袋的体积，cm3；

试验仪器采用济南中路昌试验机制造有限公司生产的微机控制电液伺服万能试验机WAW-2000D。将2 个生态袋叠加后进行单轴压缩试验，如图11 所示。试验加载速率为1 mm/min，试验终止条件依据《土工试验方法标准》［16］，本试验进行到轴向应变为20%时停止试验。

图11 测试中的生态袋Fig.11 Ecological bag under test

4.1.2 试验结果与分析

图12 为85%填充度生态袋的应力-应变关系曲线，由图12可知：应力随应变逐渐增大，应力-应变关系曲线呈明显“上翘”现象，根据《土工试验方法标准》［16］规定，对于没有峰值或稳定值的应力-应变关系曲线，取其轴向应变为15%的应力作为破坏应力，即为单轴抗压强度值qu，由试验结果得出qu=69.9 kPa。

图12 85%填充度生态袋的应力-应变关系曲线Fig.12 Stress-strain relationship curve of 85% filling degree eco-bag

生态袋在单轴压缩试验过程中，由于生态袋与填料之间的相互作用，同时考虑到生态袋是一种具有蠕变性质的材料，袋内土体在受竖向压力时，由于袋体的约束，使土体向两侧移动，最终导致呈扁平状态，即上下为平面，侧向为曲面，呈外凸状的弧形，如图13所示。

图13 生态袋单轴压缩破坏模式Fig.13 Ecological bag uniaxial compression failure mode

4.2 三轴试样无侧限抗压强度试验

4.2.1 试验准备

土样物理性质指标如表1 所示。生态袋其相关参数如表2所示。以含水率为12%，压实度为85%制备三轴试样，用生态袋在三轴试样四周进行包裹。试验仪器采用南京土壤仪器厂所生产的全自动流变三轴仪01-LH0501，试验剪切速率取1 mm/min。试验终止条件与生态袋试件单轴抗压试验的终止条件相同。

4.2.2 试验结果与分析

三轴试样的应力-应变关系曲线如图14 所示，在试验初期呈现明显的压密特性，试样的轴向应力随着轴向应变的增加而迅速增大，当轴向应变达到3%后，应力随应变的增加速率逐渐减慢，最后趋于稳定；由图14 可以得到无侧限抗压强度为75.1 kPa。

图14 生态袋包裹三轴试样的应力-应变关系曲线Fig.14 Stress-strain relationship curve of triaxial specimen wrapped in eco-bag

在试验过程中，三轴试样随着轴向应变的增加，试样鼓胀变形明显，呈现出典型的塑性破坏特征，如图15所示，这说明由于生态袋的包裹对三轴试样有侧向约束作用，明显改善了试样的变形能力。

图15 三轴试样的破坏模式Fig.15 Failure mode of triaxial specimens

4.3 结果分析对比

4.3.1 应力-应变关系曲线对比

将图12 填充度为85%生态袋的应力-应变关系曲线和图14生态袋包裹三轴试样的应力-应变关系曲线绘制到同一坐标系内，结果如图16 所示。由图16 可知：从加载前期到试样破坏（轴向应变为15%），在相同应变条件下，三轴试样的轴向应力均大于生态袋试件的轴向应力。

图16 两种试验试样的应力-应变关系曲线Fig.16 Stress-strain relationship curve of two test specimens

当轴向应变为15%时，三轴试样的无侧限抗压强度为75.1 kPa，生态袋试件的单轴抗压强度为69.9 kPa，三轴试样的无侧限抗压强度比生态袋试件大5.2 kPa，即三轴试样的无侧限抗压强度是生态袋试件的1.074 倍。在实际工程应用中，此误差值可满足实际工程的误差范围。

4.3.2 破坏模式对比

由图13、15 可知：生态袋单轴压缩破坏模式与三轴试样破坏模式相似，表明两者加筋机理相同。

5 结论

本文对不同含水率下生态袋加筋土进行三轴压缩试验，得到如下结论。

（1）不同含水率和围压下，生态袋加筋土的应力-应变曲线均未出现峰值点，表现为应变硬化型；应力-应变关系曲线符合双曲线特征；随着含水率的增加，生态袋加筋土的破坏强度均在不断减小。

（2）基于三轴试验结果，获得不同含水率下生态袋加筋土邓肯-张模型参数，分析了含水率对模型参数的影响规律，并获得以含水率为影响因子的初始切线模量经验公式，研究结果如下：黏聚力随含水率增加呈二次函数关系减小，而内摩擦角随含水率增加呈线性关系减小；试样的初始切线模量Ei随着含水率的增加而减小；破坏比变化范围为（0.828～0.990）；n值和K值均随着含水率的增大而减小，n值和K值与含水率均呈负线性关系，且相关性良好。

（3）通过对试样尺寸效应分析，表明了本文研究结论的适用性。

本文对不同含水率下生态袋加筋土进行三轴试验，研究了含水率对生态袋加筋土的力学特性和邓肯-张模型参数的影响规律，获得初始切线模量随含水率变化的经验公式；对试样尺寸效应进行分析，表明了三轴试验结果可为生态袋护坡实际工程提供支持。上述研究结论为生态袋护坡工程的设计和数值模拟提供一定的理论依据和参数支持。