基于耦合的欧拉-拉格朗日法的边坡稳定性分析
2022-10-27郝晓敏李泽莹赵燕兵
郝晓敏,李泽莹,赵燕兵
(1.山西水务口上水库开发建设管理有限公司,山西太原 030002;2.太原理工大学,山西太原 030024)
0 引言
边坡稳定分析是水工地质灾害防护的研究课题之一。有限元法作为一种常用的数值分析手段,能够有效地判别边坡的稳定性、预测边坡的稳定性系数。有限元分析中边坡的失稳判据包括:①有限元计算不收敛;②特征部位的位移拐点;③塑性区从坡脚贯通至坡顶;④能量突变法。判据①和②求得的稳定性安全系数具有唯一性,但采用传统小变形有限元法分析时,土体网格畸变导致的计算不收敛使得边坡的稳定性系数存在误差。一些研究者[1-3]认为以有限元计算不收敛作为判据存在一定的不合理性。梁艳等[1]和陈力华等[4]指出,有的边坡特征部位位移曲线的拐点不明确,单独将其作为边坡的失稳判据不具有普遍适用性。判据③具有直观性,但存在两个问题:一是塑性区贯通并不一定意味着边坡破坏[5];二是塑性区贯通的判断标准尚未统一:栾茂田等[6]最早提出了以广义塑性应变及塑性开展区作为边坡失稳的评判依据,杨才等[7]对判据③进行了优化,提出根据等效塑性应变量级指标来判定贯通时刻的塑性区贯通判据。判据④是刘新荣等[8]基于小变形有限元动力分析提出的新判据,具有唯一性和确定性。有限元动力分析通常采用显式积分算法,属于有条件收敛,因此计算结果的准确性将受到网格畸变程度的影响。上述调研表明,采用有限元法分析边坡稳定性时,存在两个问题:①失稳判据的唯一性和确定性;②有限元网格畸变对失稳判据和计算精度的影响。
当边坡土质较软及坡角较大时,边坡失稳时土体网格将产生较大变形,传统小变形有限元法的适用性将有待商榷。谭晓慧等[9]、周翠英等[10]、张士兵等[11]采用更新的拉格朗日法,分别通过可靠度分析、塑性贯通判据和有限元计算不收敛判据研究了土质边坡的稳定性,但更新的拉格朗日法仅能一定程度上解决网格畸变的问题。耦合的欧拉-拉格朗日(CEL)法作为一种结合了欧拉法和拉格朗日法优点的大变形有限元方法,不仅能很好地追踪材料自由表面的变化,并且克服了拉格朗日法网格畸变所带来的数值奇异。调研表明:①CEL 法作为一种有效的大变形有限元分析技术,目前还未在边坡稳定分析中得到广泛应用;②边坡失稳判据较多,对于CEL 法来讲,采用哪种判据最为有效。本文将基于大变形有限元分析技术CEL法,分析土质边坡的稳定性,探讨不同判据在CEL 法中的适用性;并开展模型参数考察,建立用于计算土质边坡稳定性系数的经验公式,便于工程人员使用。
1 耦合的欧拉-拉格朗日(CEL)法模型及验证
本文将基于CEL法,结合强度折减法[12,13],分析土质边坡的稳定性。CEL 法结合了拉格朗日(Lagrangian)法和欧拉(Eulerian)法的优点,将拉格朗日法和欧拉法的计算模式交替使用,能有效避免网格畸变对失稳判据和计算精度的影响[14,15]。CEL 法采用了显式积分算法,后一步的计算结果由前一步的计算结果代入获得,不存在计算不收敛的问题;CEL 法采用体积分数比来追踪材料表面的变形,无法捕捉边坡坡顶或坡脚的位移突变。因此,CEL 法不适用边坡失稳判据①和②。CEL 法属于动力分析方法,能够准确计算边坡的能量变化及追踪边坡的塑性屈服过程,判据③和判据④将是本文讨论的重点。
1.1 强度折减法的基本原理
强度折减法是利用折减系数Fr对土体强度指标c和ϕ进行折减,直到满足失稳判据。采用强度折减法确定的边坡发生失稳破坏时对应的折减系数即为边坡稳定性系数Fs。折减后的土体强度指标分别为:

式中:c和ϕ分别为土体的黏聚力和内摩擦角;cm和ϕm分别为折减后土体的黏聚力和内摩擦角。
有限元计算过程中,采用设置场变量的方式,将c和ϕ值与Fr关联,逐渐增大Fr,由式(1)和(2)可知,cm和ϕm将逐渐减小,直至边坡满足失稳判据发生破坏。
1.2 CEL模型的建立与计算结果
模型为一典型均质土坡,有限元模型如图1所示,模型及土体参数见表1。基于有限元分析软件ABAQUS 进行建模,模型采用平面应变分析。为捕捉边坡失稳后坡顶及破面的变形情况,建立了空气层,见图1。土体采用理想弹塑性模型,服从莫尔-库仑屈服准则。

图1 CEL模型(单位:m)Fig.1 CEL model

表1 模型及土体参数Tab.1 Parameters for model and soil
分析中,给土体施加重力载荷,通过强度折减,边坡将发生失稳破坏。基于能量守恒原理,当边坡失稳破坏时重力做功,边坡的重力势能转化为内能和动能。模型采用了动力计算模块,可在计算结果中通过历史变量输出模块,直接提取边坡的重力势能、内能和动能曲线。图2 表明,随着折减系数Fr的增大,重力势能、内能和动能曲线在Fr=0.99 时出现突然增大的趋势。边坡处于稳定状态时,模型动能为零;边坡失稳破坏时,模型动能将突然增大[图2(b)],动能突变更具直观性,因此本文以动能突变作为能量突变法(判据④)的首选判据。

图2 折减系数与边坡能量关系曲线Fig.2 Relationship between reduction coefficient and slope energy
CEL 法可以计算获得土体的累积塑性应变值(PEEQ),PEEQ 大于零时表明土体产生塑性破坏。当边坡从坡脚至坡顶产生一连续的塑性贯通区时,即该区域内土体的PEEQ 值均大于某一临界PEEQ(Pc)值时,认为边坡发生失稳破坏,即判据③。研究者们对Pc的取值存在争论,不同的Pc值将获得不同的边坡稳定性系数。图3 给出了不同Pc值下边坡的塑性贯通面,Pc=0.005、0.01、0.05时,边坡稳定性系数分别为1.02、1.03、1.09,且随着Pc值的增大而增大。

图3 塑性贯通面Fig.3 Plastic failure zone
1.3 模型考察
CEL 法作为一种新型大变形有限元分析技术,尚未广泛应用于分析土质边坡的稳定性,因此,需事先考察影响模型计算精度的相关参数。本节以动能突变判据为例,基于图1 所示的数值模型,考察模型网格尺寸和模型计算时长对计算结果的影响。模型计算分两步执行,第一步为初始地应力步,赋予边坡初始应力状态;第二步为强度折减步,对土体强度指标进行折减,直至边坡失稳破坏。考察中设置了3 种网格尺寸,即H/10、H/20、H/40,其中,H表示边坡的坡高,3 种网格尺寸下边坡的稳定性系数Fs分别为1.02、0.99、0.98。结果表明,随着网格尺寸的减小,边坡稳定性系数Fs逐渐收敛。综合考虑计算效率与计算精度,计算中网格尺寸采用H/20。另外,考察了不同初始地应力步时长ts和不同强度折减步时长tr对边坡的稳定性系数的影响。当ts=0.001、0.01和0.1 s时,边坡稳定性系数Fs均为0.99,因此,边坡稳定性系数不受初始地应力步时长的影响;当tr=2、5、10、20 和40 s时,边坡稳定性系数Fs分别为1.08、1.05、1.02、0.99 和0.98,Fs随强度折减步计算时长tr的增大而逐渐减小,最后趋于收敛。为保障计算结果的唯一性,分析中ts采用0.01 s,tr采用20 s。图4给出了初始地应力对动能曲线的影响效应,图4表明施加土体地应力不影响边坡稳定性系数Fs,但能有效的降低动能曲线的震荡幅度。

图4 地应力对动能曲线的影响Fig.4 Effect of initial geostatic stress on the kinetic energy curve
1.4 模型验证与分析
赵尚毅等[5]、Dawson 等[12]、Chen 等[16]曾采用有限元法分析了土质边坡的稳定性,并计算了边坡的稳定性系数Fs,计算结果见表2。本节将与三位研究者的计算结果进行对比,验证模型的有效性。计算模型设置与图1 中所示模型保持一致,采用动能突变判据(判据④),计算了边坡的稳定性系数Fs,计算结果见表3。对比表2 和表3 发现,CEL 法采用动能突变法判据求得算例1 至3 的边坡稳定性系数分为为1.57、0.99、1.35;赵尚毅等[5]、Dawson 等[12]、Chen 等[16]的计算结果分别为1.56、1.00 和1.30,最大误差仅为3.7%,验证了CEL法的有效性。

表2 边坡算例的土体材料参数及计算结果Tab.2 Soil properties and calculated results of different slope cases
本文同样进行了小变形有限元计算,并与大变形有限元CEL 法的计算结果进行对比(表3),用于探讨各类判据的差异性。表3表明,对于算例1和2(坡角β≤45°),判据④与计算不收敛法(判据①)的计算结果吻合较好,最大偏差仅为1.0%;判据④与特征部位的位移拐点(判据②)最大偏差为1.3%。当坡角β≤45°,判据①、②和④求得的边坡稳定性系数相近,最大偏差仅为2.0%。对于算例3(坡角β=76°),判据④与判据①偏差仅为0.7%,与判据②偏差达到8.0%。当边坡坡角较大时,特征点较易发生位移突变,但此时并不意味着边坡发生失稳破坏。综上分析表明,不同坡角下判据④与判据①计算结果吻合较好;对于高边坡,判据②可能会低估边坡稳定性系数。
对于塑性区从坡脚贯通至坡顶判据(判据③)中如何选择贯通的标准一直存在争论。本文将提出临界累计塑性应变(Pc)的概念,当塑性贯通区的累计塑性应变值均大于Pc时,即判定形成塑性贯通带,边坡发生失稳破坏,进而量化判据③计算的边坡稳定性系数。表3表明,对于算例1和2(坡角β≤45°),小变形有限元计算中当累计塑性应变超过某一Pc时,稳定性系数保持不变,此时的稳定性系数即为判据③求得的稳定性系数,且判据③与判据①和②相差较小。对于算例3(坡角β=76°),小变形由于网格畸变导致计算不收敛,使得未出现塑性贯通区。大变形有限元计算结果显示,随着Pc值的增大,稳定性系数逐渐增大,使得稳定性系数不具有唯一性。因此,建议CEL 法采用动能突变法作为边坡失稳的判据。

表3 不同判据对应的边坡稳定性系数Tab.3 Different safety factors with different criteria for soil slopes
2 边坡稳定性系数的经验公式
基于图1 所示的数值模型进行参数考察,所涉及的参数包括:坡高、坡角、内摩擦角、黏聚力和土体重度。参考工程实际考察各参数对边坡稳定性系数的影响,坡高H分别为5、10、15、20 m;坡角β为15°、30°、45°、60°、75°;土体重度γ为16、18、20 kN/m3、黏聚力c为5、10、20、30、40 kPa;内摩擦角φ为5°、10°、20°、30°、40°,共计113 个计算工况。李泽莹[17]提出如下经验公式:

基于113个计算工况所得结果,对式(3)进行拟合。当15°≤β<60°时,A=7.19,B=0.82,C=0.21,D=0.97,E=1.22,F=0.11;当60°≤β<75°时,A=6.31,B=0.86,C=0.24,D=1.59,E=2.96,F=0.20。图5 给出了式(3)与有限元模型计算结果的相关,当15°≤β<60°,相关系数R2为0.99;当60°≤β<75°时,相关系数R2为0.96,证明了公式(3)的拟合效果很好。
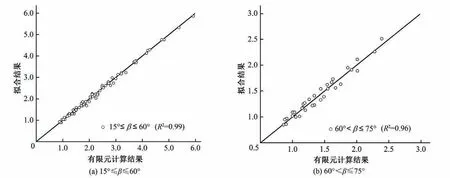
图5 拟合结果与有限元计算结果对比Fig.5 Comparison between fitting results and finite element calculation results
为验证式(3)的有效性,将与条分法、简化毕肖普法及孙超伟等[18]的计算结果进行对比,见表4。表4 表明,式(3)的计算结果与条分法、简化毕肖普法及孙超伟等[18]的计算结果的相对差值分别为2.6%、5.9%和4.7%,证明公式(3)具有一定的有效性。
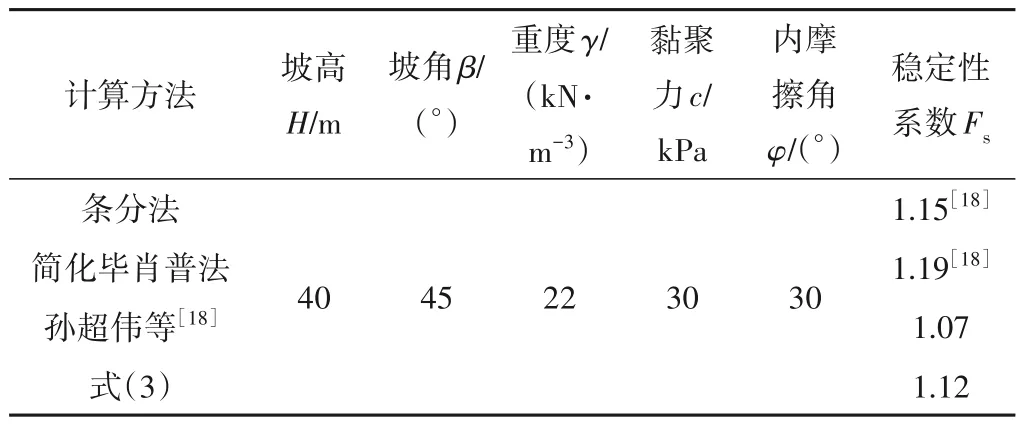
表4 经验公式验证Tab.4 Verification of the empirical formula
3 结论
(1)基于大变形有限元分析技术CEL 法分析了土质边坡的稳定性,分析了网格尺寸、计算时长和初始地应力对边坡稳定性系数的影响,并验证了CEL法的有效性。
(2)探讨了塑性区从坡脚贯通至坡顶判据及能量突变法判据在CEL法中的适用性,建议采用能量突变法判据。
(3)针对塑性区从坡脚贯通至坡顶判据,提出了临界累计塑性应变Pc的概念,量化了采用塑性区从坡脚贯通至坡顶判据计算的边坡稳定性系数,但在CEL 法中如何选取Pc值还需进一步的研究。
(4)获得了用于计算土质边坡稳定性系数的经验公式,公式可反映坡高、坡角、内摩擦角、黏聚力和土体重度的影响。
