准二维空间中的隐秘涡旋量子液滴*

陈逸熙 蔡晓妍 刘彬2)† 江迅达2) 黎永耀2)

1) (佛山科学技术学院物理与光电工程学院,佛山 528225)

2) (佛山科学技术学院,物理与光电工程学院粤港澳智能微纳光电技术联合实验室,佛山 528225)

本文探究了弱囚禁条件下玻色-玻色混合凝聚体中的准二维隐秘涡旋量子液滴及其动力学特性.前期研究表明,在完全自由的三维空间中,隐秘涡旋量子液滴难以稳定;在二维系统中,当囚禁尺度是窄囚禁条件时,系统仅支持拓扑荷 S1,2=±1 的隐秘涡旋量子液滴;因此当横向囚禁尺度较弱时,准二维空间中李-黄-杨修正项仍然采用三维空间中的表达式来描述,此时隐秘涡旋量子液滴能否保持稳定是一个重要的科学问题.本文采用虚时间方法获得了拓扑荷 S1,2 达到 ± 4 的隐秘涡旋量子液滴;进一步论证了隐秘涡旋量子液滴的有效面积 Aeff 和化学势 µ 与总粒子数 N 之间的依赖关系;并采用线性稳定性分析结合实时传输方法获得了总粒子数临界值 Nth 分别与拓扑荷 S1 和非线性系数 δg 之间的依赖关系.在动力学部分,本文研究了由两个不同拓扑荷的隐秘涡旋量子液滴构造的复合涡旋模式,即嵌套涡旋量子液滴.结合量子液滴的密度分布具有“平顶型”的特点,采用Thomas-Fermi 近似对数值结果进行了有效验证.

1 引言

自玻色-爱因斯坦凝聚(Bose-Einstein condensates,BEC)在实验上实现以来,其作为一个宏观量子态得到了人们的广泛研究,其中自局域态的稳定性及动力学问题是冷原子领域和非线性科学研究的热点问题,例如物质波孤子的研究[1-16].通常原子间的接触相互作用表现为排斥相互作用,因此一旦失去外势的囚禁,气体就会膨胀而弥散在空间中,尽管可以通过Feshbach 共振技术将排斥相互作用调成吸引相互作用,但是在高维情况下,原子间的吸引相互作用会使BEC 展现出动力学不稳定性,从而在很短的时间内导致BEC 的坍塌.为实现高维自由空间中的稳定自局域态,最常用的方法是对三次非线性吸引作用进行修正,如引入竞争型非线性、饱和非线性或非局域非线性等[17-23];另一方面,通过引入自旋-轨道耦合[24-27]、谐振子势[28]或晶格周期势[29,30]等也有助于获得稳定的非线性自局域态.

近年来,基于李-黄-杨(Lee-Huang-Yang,LHY)修正项所描述的量子液滴的实验实现突破了高维系统中仅有吸引相互作用时不能形成稳定自局域态的限制[31,32].这里用于解释量子液滴形成机制的LHY 修正项源于绝对零度附近的量子涨落效应,其提供了一个高阶的排斥效应去阻止因吸引相互作用引起的坍塌,是20 世纪50 年代由3 位著名的华人科学家李政道、黄克孙和杨振宁所建立[33].研究表明: 量子液滴的表现形式及动力学演化模型可以采用平均场近似下的Gross-Pitaevskii (GP)方程中加入LHY 修正项来描述[34-49].随后,量子液滴在极性原子气体和非极性的玻色气体中获得广泛关注,如玻色-费米组成的异核原子系统中利用自旋轨道耦合形成的量子液滴被研究[50];偶极的Dy 凝聚体中,短程三体排斥力可以稳定自束缚量子液滴[51];由Na 和Rb 混合的量子液滴在实验上被实现[52];弯月型超稀量子液滴[53]和半离散涡旋量子液滴被研究[54].结构空间的引入也为量子液滴的研究带来新思路,如一维和二维光晶格中量子液滴的动力学及多稳特性的研究[55-57].

特别地,在二维模型中,当横向囚禁尺度相当窄时(远小于1 µm),二维涡旋量子液滴是稳定的[58],当撤掉这个囚禁条件,在完全自由的三维空间中,当两个分量具有相同拓扑荷时可以形成稳定的涡旋量子液滴.但是,当两个分量的拓扑荷数相反时,即形成隐秘涡旋模式,Kartashov等[59]证明在该条件下隐秘涡旋模式是不能稳定存在的.然而,在前期研究中发现,当横向囚禁尺度是窄囚禁条件时,即此时的LHY 修正项是对数函数形式,隐秘涡旋模式是可以稳定存在的,但仅仅支持拓扑荷S1,2=±1的模式.因此,一个有趣的问题是当横向囚禁尺度变得宽松,即弱囚禁条件,隐秘涡旋模式能否稳定存在? 若能,能否突破S1,2=±1 的限制.实验中大多数的二维囚禁系统,横向囚禁尺度往往都大于1 µm,因此远大于量子液滴窄囚禁的尺度,在此条件下,LHY 修正项就不能再由对数函数来描述,而必须采用全三维空间中的LHY 修正项表达式.与对数函数不同的是,全三维空间的LHY修正项仅表现出排斥相互作用[60],因而其非线性动力学与窄囚禁时的机制存在差别.本论文研究在弱囚禁条件下,当LHY 修正项采用全三维空间中的表达式,系统能否支持隐秘涡旋模式的存在.

本工作证明在弱囚禁条件下,玻色-玻色混合凝聚体形成的量子液滴不仅可以支持隐秘涡旋模式的存在,而且突破了S1,2=±1 的限制.同时,也确定了这些模式的稳定阈值.最后,研究了由不同拓扑荷的隐秘涡旋量子液滴形成的嵌套涡旋模式的动力学特性.

2 理论模型

基于以上的研究背景,结合参考文献[61]中的补充材料,系统的GP 方程组可以表示成如下形式:

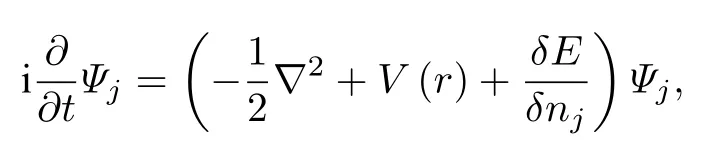
其中nj=|Ψj|2(j=1,2),Ψ1,2代表两组分BECs 的波函数,E=EMF+ELHY表示平均场的能量和LHY修正项的能量,具体可以表示为

将定态解和谐振子势函数的表达式代入方程组(3),并对方程组在z方向上进行积分,可以得到降维后的准二维GP 方程组,形式如下:

式中,S1,2分别代表两分量的涡旋拓扑荷数,µ表示化学势,将表达式(7)代入方程组(6),可获得径向波函数ϕ1,2满足的径向方程组,形式如下:

在数值模拟的过程中,关于稳定性的判断,采用线性稳定性分析方法结合实时传输方法进行验证.下文将介绍线性稳定性分析方法的具体思路[62,63].首先,假设扰动解的具体形式为

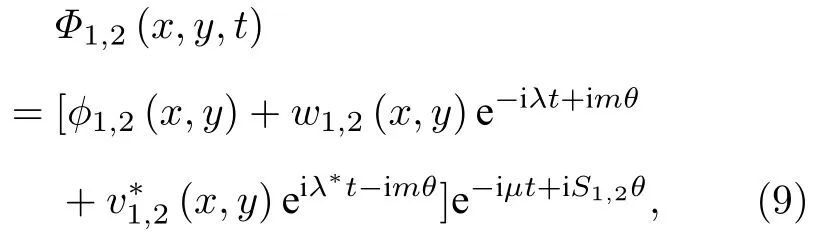
式中λ表示不稳定增长率,w1,2和v1,2表示不稳定增长率所对应的本征模式,m表示对涡旋拓扑荷数的扰动.将(9)式代入GP 方程组(6)并线性化后有:

其中F11—F44的具体表达形式详见附录部分.与一维线性稳定性分析不同的是,这里有对涡旋拓扑荷数的扰动,且在涡旋拓扑荷数扰动值至少取m=0,1,2,3 时,若不稳定性增长率λ没有虚部出现,则说明此时的隐秘涡旋量子液滴解稳定,反之则不稳定.

3 结果分析

在上述模型中,采用虚时间方法[64]求解归一化方程组(6)的定态解,并获得了拓扑荷最大为S1,2=±4的稳定隐秘涡旋量子液滴,突破了窄囚禁条件下S1,2=±1 的限制.图1 是隐秘涡旋量子液滴的典型例子,展示了S1,2分别为±3 和±4 时的隐秘涡旋量子液滴,其中图1(a1),(a2),(c1),(c2)分别表示两分量的密度分布,可以看出隐秘涡旋量子液滴的密度分布具有环形分布的特点.图1(b1),(b2),(d1),(d2)分别展示了其对应的相位分布,可以清晰看出两个分量的相位结构相反.同时,从密度分布图可以看出,随着拓扑荷和总粒子数的增加,隐秘涡旋量子液滴的内半径逐渐增大.与文献[60]中的结果一致,随着总粒子数的增加,隐秘涡旋量子液滴密度分布也展现出“平顶型”的特征.

图1 隐秘涡旋量子液滴的典型例子 (a1),(a2)总粒子数 N=2500 时,拓扑荷为S1,2= ±3 的两分量密度分布图;(b1),(b2) 分别对应其相位分布;(c1),(c2)总粒子数 N=30000 时,拓扑荷为S1,2= ±4 的两分量的密度分布图;(d1),(d2) 分别对应其相位分布.系统参数为g=10 和δg=0.5Fig.1.Typical examples of stable hidden vortices of QDs: (a1),(a2) Density patterns of the two components with(N,S1,2)=(2500,±3);(b1),(b2) the corresponding phase diagrams of the hidden vortices of QDs are in panels (a1) and (a2),respectively;(c1),(c2) density patterns of the two components with (N,S1,2)=(30000,±4);(d1),(d2) the corresponding phase diagrams of the hidden vortices of QDs are in panels (c1) and (c2),respectively.The other parameters are g=10 and δg=0.5.

为进一步研究隐秘涡旋量子液滴的特性,定义其有效面积为

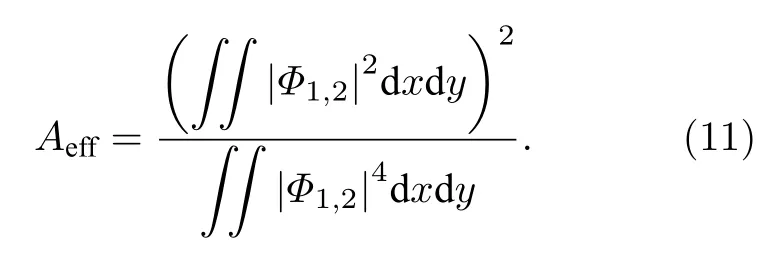
图2(a)展示了隐秘涡旋量子液滴的有效面积与总粒子数之间的依赖关系.图中黑色点虚线表示不稳定区域,红色实线表示稳定区域,蓝色的点表示稳定与不稳定区域的总粒子数临界值Nth,其中稳定与不稳定的隐秘涡旋量子液滴的典型例子将在图3 中展示.从图2(a)可以看出,在稳定区域内,隐秘涡旋量子液滴的有效面积随着总粒子数的增加而线性增大,其主要原因是: 当总粒子数足够大时,其密度分布会展现“平顶型”,记峰值密度,若继续增加总粒子数,峰值密度保持不变,此时峰值密度与有效面积的乘积即为总粒子数,即有N≈2Aeffnmax.根据已有数据分析,在δg=0.5 时,有峰值密度nmax≈0.0217,图2(a)中红色实线的斜率大约为2 3.87,即大约为1/(2nmax),因此很好地说明了有效面积与总粒子数之间的线性增大规律.

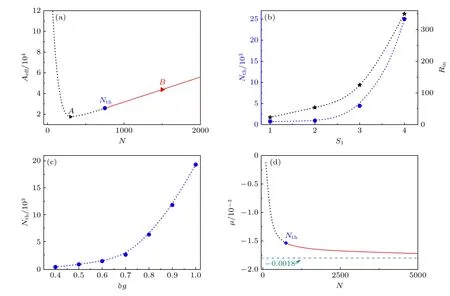
图2 (a) 隐秘涡旋量子液滴的有效面积 Aeff 与总粒子数 N 之间的依赖关系,Nth 表示稳定与不稳定区域的临界值,红色实线表示稳定区域,黑色点虚线表示不稳定区域;(b) 蓝色点表示固定 δg=0.5 时,临界值 Nth 与拓扑荷 S1 之间的依赖关系;黑色“★”表示临界值下的隐秘涡旋量子液滴的内半径大小 Rin;(c) 固定 S1,2=±1 时,不同 δg 值下的临界值 Nth;(d) 固定 S1,2=±1 时,化学势 µ 与总粒子数 N 之间的依赖关系Fig.2.(a) The dependence of the effective area Aeff on the norm N of the hidden vortices of QDs,Nth is the threshold norm,red solid curve shows the stable region and the black dash curve shows the unstable region;(b) the blue dot represents the dependence of the threshold Nth on the topological charge S1 when δg=0.5,the black star represents the inner radius of the hidden vortices of QDs at the threshold norm;(c) the threshold norm Nth for hidden vortices of QDs with S1,2=±1 as a function of δg;(d) the dependence of the chemical potential µ on the total norm N with S1,2=±1.

在模拟的过程中发现,存在临界值Nth,当总粒子数N ＞Nth时,隐秘涡旋量子液滴是稳定的,反之则不稳定.对稳定性的验证采用检验本征值λ的不稳定增长率与实时传输相结合的方法.图2(b)探讨了固定 δg时,临界值Nth与拓扑荷S1之间的依赖关系,从蓝色点可以看出随着拓扑荷数的增加,临界值逐渐增加;同时也展示了临界值下的隐秘涡旋量子液滴的内半径大小Rin[见黑色“★”],可以看出随着拓扑荷数的增加,内半径Rin逐渐增大.图2(c)展示了固定拓扑荷S1,2=±1 时,临界值Nth与δg之间的关系,同样可以看出随着 δg的增加临界值也增加.

进一步探究固定S1,2=±1 时,化学势µ与总粒子数N之间的关系.从图2(d)可以看出,µ-N之间的依赖关系满足Vakhitov-Kolokolov 判据,即满足 dµ/dN＜0;同时发现随着总粒子数的增加,其化学势µ→-0.0018 不变.下面给出其理论解释.

当总粒子数足够大,隐秘涡旋量子液滴形成时其密度分布具有“平顶型”的特征,此时可以采用Thomas-Fermi (TF)近似,即忽略动能项的影响,系统的能量密度可以表示为

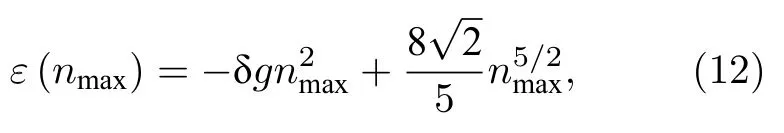
此时系统的总能量为能量密度与有效面积的乘积,即有

(13)式也很好地解释了当涡旋量子液滴的密度分布达到“平顶型”时,总能量随着总粒子数线性增长.当总粒子数N一定时,系统将选择nmax使得总能量最低,即有 dE/dnmax=0,可得

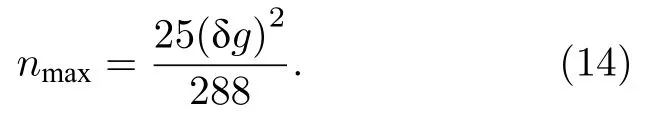
例如,取 δg=0.5,可得峰值密度nmax≈0.0217,从图1 中的显示色条可以看出此理论分析与数值结果一致.

根据方程组(8),可以得到在TF 近似下化学势与峰值密度之间的关系为

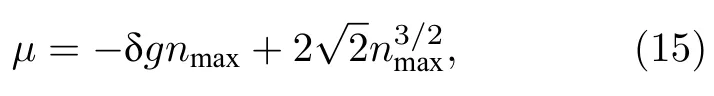
结合 (14) 式,可知µ→-0.0018,与图2(d)的数值结果一致.

图3 分别展示了S1,2=±1 时,具有不同总粒子数N的隐秘涡旋量子液滴不稳定传输与稳定传输的典型例子,其分别对应图2(a)中的点“A”和点“B”.图(a1)—(a3)分别展示了总粒子数N=300

时,Φ1分量传输到t=0,t=7300和t=10000 时密度分布情况,显然此参数下隐秘涡旋量子液滴是不稳定的;图(b1)—(b3)分别展示了总粒子数N=1500 时,Φ1分量稳定传输到t=0,t=5200和t=10000时密度分布情况.图3(a4),(b4)分别展示了涡旋拓扑荷的扰动值m=0,1,2,3 时扰动本征值λ的实部与虚部之间的关系,可以看出当扰动本征值的虚部为0 时,隐秘涡旋量子液滴传输稳定,反之当扰动本征值的虚部不为0 时,传输不稳定,表明线性稳定性分析的结果与实时传输的结果一致.

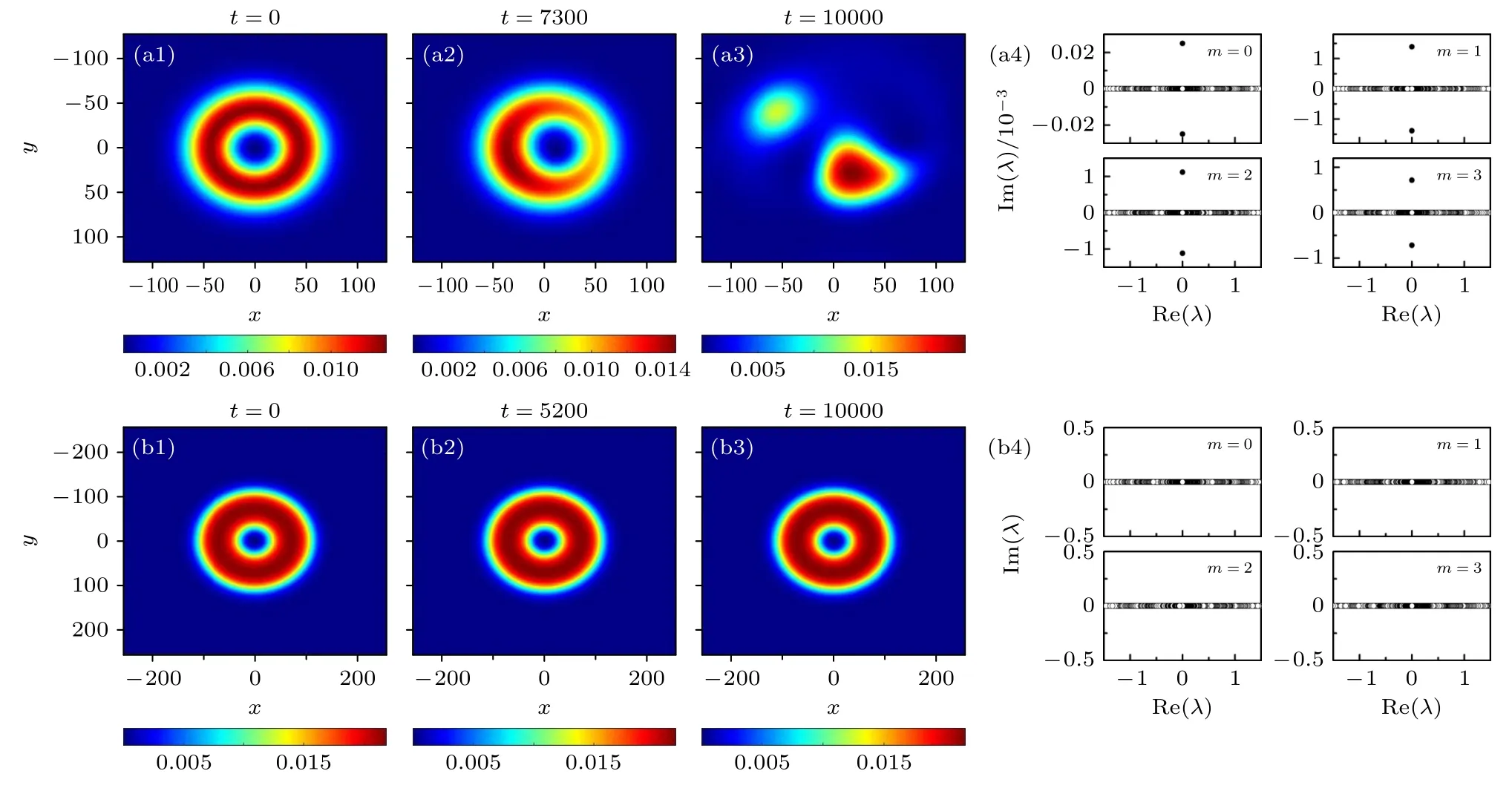
图3 (a1)—(a3) N=300 时,Φ1 分量传输到 t=0,t=7300 和 t=10000 时密度分布情况,显然此时传输不稳定;(a4)涡旋拓扑荷数的扰动值m=0,1,2,3时不稳定增长率 λ的实部和虚部的关系图;(b1)—(b3) N=1500 时,Φ1分量传输到 t=0,t=5200 和 t=10000 时密度分布情况,显然此时传输稳定;(b4)涡旋拓扑荷数的扰动值 m=0,1,2,3 时不稳定增长率 λ 的实部和虚部的关系图Fig.3.(a1)—(a3) The density pattern of the Φ1 component with N=300 and t=0,7300,10000,which is obviously unstable;(a4) perturbation eigenvalues for the corresponding hidden vortices of QDs with N=300 and S1,2=±1 for different azimuthal index m=0,1,2,3;(b1)—(b3) the density pattern of the Φ1 component with N=1500 and t=0,5200,10000;(b4) perturbation eigenvalues for the corresponding hidden vortices of QDs with N=1500 and S1,2=±1 for different azimuthal indexm=0,1,2,3.

4 动力学

嵌套涡旋指的是在多组分系统中,每个组分携带不同的拓扑荷且嵌套在一起的涡旋结构.目前,对由隐秘涡旋量子液滴形成的嵌套涡旋尚未被研究,在这一部分主要探讨两个隐秘涡旋量子液滴之间形成的嵌套涡旋量子液滴.研究发现,较大拓扑荷数的隐秘涡旋量子液滴具有较大的内半径Rin[参见图2(b)中的黑色“★”],因此其内部具有较大的空间来嵌套外半径较小的其他涡旋量子液滴.如果嵌入的涡旋量子液滴的外半径与被嵌入的涡旋量子液滴的内半径之间有足够的空间,那么此两个嵌套在一起的嵌套涡旋量子液滴可以稳定共存一段时间.

图4 给出了嵌套涡旋量子液滴的典型例子,这里仅展示Φ1分量.图4(a1)—(a3)和(c1)—(c3)分别展示了一组拓扑荷小的隐秘涡旋量子液滴(N=800,S1,2=±1),被嵌入到内半径较大的隐秘涡旋量子液滴中(N=30000,S1,2=±4 和N=30000,S1,2=∓4),结果表明其形成的嵌套涡旋量子液滴可以稳定共存且达到t=10000;图4(a4),(c4)分别展示了嵌套涡旋量子液滴分别传输到 1 0000 时的相位分布,结果显示其相位分布结构完好.图4(b1)—(b3)和(d1)—(d3)分别展示了N=800,S1,2=±1的隐秘涡旋量子液滴被嵌到N=26000,S1,2=±4和N=26000,S1,2=∓4 的隐秘涡旋量子液滴中的传输结果,可以看出当两个隐秘涡旋量子液滴的内外半径之间的距离较小时,形成的嵌套涡旋量子液滴是不能够长时间稳定共存的,因相互吸引并最终融合在一起;图4(b4),(d4)分别展示嵌套涡旋量子液滴传输到t=4500 和t=6400 时的相位分布.其密度分布和相位结构与初始状态相比均发生了变化,反映了此时形成的嵌套涡旋量子液滴是不稳定的.

图4 嵌套涡旋的典型例子 (a1)—(a3) N=800,S1,2=±1 和N=30000,S1,2=±4 嵌套形成的嵌套涡旋量子液滴;(a4) 液滴传输到 t=10000 时的相位分布;(b1)—(b3) N=800,S1,2=±1 和N=26000,S1,2=±4嵌套形成的嵌套涡旋量子液滴;(b4) 液滴传输到 t=4500 时的相位分布;(c1)—(c3) N=800,S1,2=±1 和N=30000,S1,2=∓4 嵌套形成的嵌套涡旋量子液滴;(c4) 液滴传输到 t=10000 时的相位分布;(d1)—(d3) N=800,S1,2=±1 和N=26000,S1,2=∓4 嵌套形成的嵌套涡旋量子液滴;(d4) 液滴传输到 t=6400 时的相位分布Fig.4.Typical examples of the nested vortex QDs: (a1)—(a3) The hidden vortices of QDs with (N,S1,2)=(800,±1) nests inside(N,S1,2)=(30000,±4),which has a larger inner radius;(a4)output pattern of the phase structure for the nested hidden vortices of QDs at t=10000;(b1)—(b3) the hidden vortices of QDs with (N,S1,2)=(800,±1) nests inside (N,S1,2)=(26000,±4);(b4) output pattern of the phase structure for the nested hidden vortices of QDs at t=4500;(c1)—(c3) the hidden vortices of QDs with (N,S1,2)=(800,±1) nests inside (N,S1,2)=(30000,∓4);(c4) output pattern of the phase structure for the nested hidden vortices of QDs at t=10000;(d1) —(d3) the hidden vortices of QDs with (N,S1,2)=(800,±1) nests inside(N,S1,2)=(26000,∓4);(d4) output pattern of the phase structure for the nested hidden vortices of QDs at t=6400.

5 结论

本文主要研究弱囚禁条件下玻色-玻色混合凝聚体中的隐秘涡旋量子液滴及其动力学特性.当横向囚禁尺度相当窄时(远小于1 µm),二维涡旋量子液滴是稳定的,同时也仅支持拓扑荷S1,2=±1的隐秘涡旋量子液滴的存在,此时系统中的LHY修正项由对数函数来描述.当撤掉囚禁,在完全自由的三维空间中,虽然能形成稳定的涡旋量子液滴,但是不能形成稳定的隐秘涡旋量子液滴.然而,实验中大多数的二维囚禁系统,一般其横向囚禁尺度远大于1 µm (弱囚禁),此时LHY 修正项就不再由对数函数来描述,而是采用全三维空间中的LHY 修正项表达式,因此量子液滴将具有与窄囚禁下不同的非线性动力学特性.本文以此为出发点,采用虚时间方法获得了弱囚禁下拓扑荷数达到S1,2=±4的隐秘涡旋量子液滴,其密度分布具有环形结构特征,并给出了不同拓扑荷数下的隐秘涡旋量子液滴的稳定与不稳定的粒子数临界值Nth.研究表明: 在稳定区域内,隐秘涡旋量子液滴的有效面积随着总粒子数的增加而线性增大;稳定隐秘涡旋量子液滴的化学势与总粒子数之间的关系满足Vakhitov-Kolokolov 判据,即满足 dµ/dN＜0,并随着总粒子数的增加趋于-0.0018 不变;文中结合量子液滴“平顶型”的特征,采用Thomas-Fermi近似对数值结果进行了验证,其理论分析与数值结果一致.最后,本文利用两个不同拓扑荷的隐秘涡旋量子液滴构造了新的复合涡旋模式,即嵌套涡旋;结果表明当嵌入的涡旋量子液滴的外半径与被嵌入的涡旋量子液滴的内半径之间有足够的空间时,两个嵌套在一起的嵌套涡旋量子液滴可以稳定共存.因此,量子液滴在弱囚禁条件下对隐秘涡旋的支持要优于完全自由和窄囚禁条件的量子液滴,其为隐秘涡旋的稳定存在提供了一个更宽松的环境.本文的研究结果为其他系统中实现隐秘涡旋量子液滴提供参考,并为涡旋量子液滴的实验实现提供理论依据.

附录

F11—F44的具体表达式如下: