基于多源数据的水利工程施工复合地基承载力估算研究

2022-10-27惠伟伟罗小玲伍芝铭李春宇

科学技术创新 2022年31期

惠伟伟，罗小玲，伍芝铭，李春宇

（1.重庆市南岸区农业农村委员会，重庆 400000；2.重庆市水利电力建筑勘测设计研究院有限公司，重庆 400000）

引言

随着国内经济及社会的发展，水利工程也得到了大规模发展。水利工程一般建设在坚硬岩层上，这表明水利工程对地基的要求较高，当在水利工程施工现场遇到淤泥质土等软弱地基时，常需采用相应的地基处理方法以增加提高工程的稳定性[1-2]。相关规范中规定的水利工程地基处理的常用方法主要包括了垫层法、排水固结法、强夯置换法和复合地基等，其中复合地基由于其施工较简单、造价低、承载力高，被广泛应用于水利工程地基处理中[3-6]。由于不同材料不同施工工艺的复合地基承载力不同，因此在实际施工过程中需采用一定的方法得出地基承载力，现有水利工程地基承载力常采用载荷试验法获得，但这种方法周期长、造价高[7]，因此，找出合理的复合地基承载力的计算模型成为国内相关领域研究的热点。由于复合地基承载力与施工工艺、桩体直径、原地基性质等多个因素有关，传统的经验模型方式无法完全表征地基承载力与各影响因素之间的非线性关系，因此采用机器学习模型构建复合地基承载力估算模型是十分必要的。传统的机器学习模型常由于其参数的随机化选择，导致模型计算结果的不确定性较强，从而影响模型精度。为避免这一现象的发生，常需采用优化算法对模型进行优化，从而降低模型不确定性，提高模型精度。为得出适宜于水利工程复合地基承载力估算模型，本研究以CFG 桩为例，以人工神经网络模型（ANN）为基础，基于布谷鸟搜索算法（CSA）、粒子群算法（PSO）和遗传算法（GA），构建3 种优化模型，基于状体直径、土体孔隙比等多源数据，实现水利工程复合地基承载力的高精度估算。

1 模型原理

1.1 人工神经网络模型

人工神经网络模型（ANN）已被广泛应用于数据估算领域中。它是一种模拟人脑工作的信息处理系统，由输入层、隐藏层和输出层3 部分组成，包括了数据收集、学习、适应、模式识别和目标输出共5 个步骤。

1.2 布谷鸟算法优化ANN 模型

Yang 和Deb[8]于2009 年基于布谷鸟的生活习性提出了布谷鸟优化算法（CSA）。CSA-ANN 模型可提高传统模型收敛速度和精度。布谷鸟在现实生活中为提高繁殖率，常将自己的蛋混在其他宿主鸟窝中，同时布谷鸟幼崽为了继续生存需模仿宿主鸟的生活习性。

1.3 粒子群算法优化ANN 模型

粒子群算法（PSO）由Eberhart 和Kennedy 在1995年提出[9]，在算法中，将每个输入因子定义为一个粒子，每个粒子的潜在解对应一个适应度函数。该算法分别通过单个极值和全局极值更新粒子的速度和位置。

1.4 遗传算法优化ANN 模型

Holland 等[10]根据生物进化和适者生存的原则提出了遗传算法（GA），在GA-ANN 中，引入交叉和突变处理对个体适应度的计算值进行更新，通过判断适应度是否满足误差要求得到最终输出结果。

1.5 算法性能测试

为测试3 种算法的性能，引入3 种标准测试函数，算法函数的公式如下：

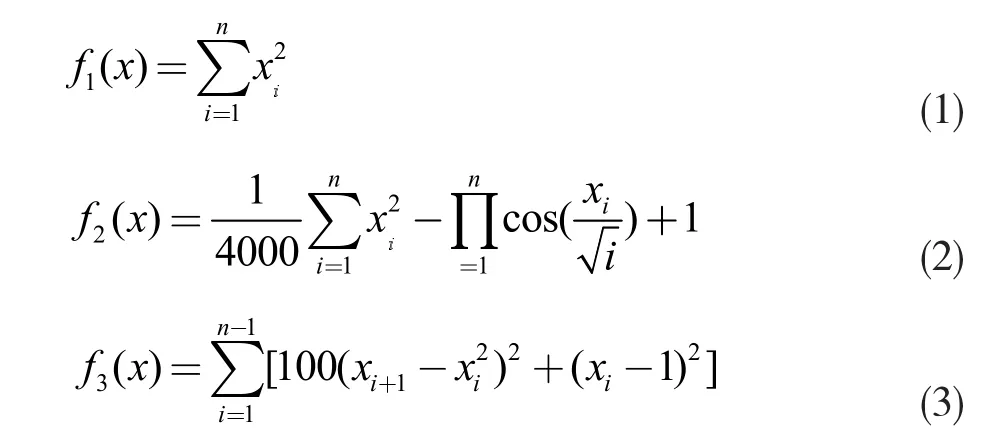
3 种算法的性能结果可见图1。由图中可以看出，CSA 算法在迭代速率和计算精度上均最高。

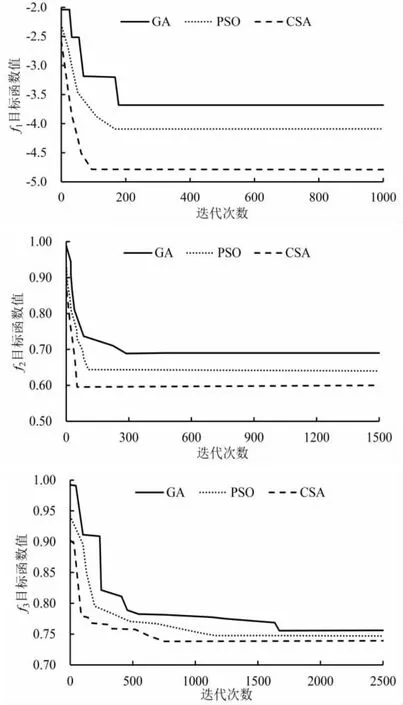
图1 不同算法迭代测试情况

1.6 模型精度对比

由于复合地基承载力与土地性质、桩体大小等多种因素有关系，为保证模型精度，需引入多源数据训练模型，本研究基于20 个样本的实测数据，将1～15个样本数据用于训练模型，16～20 号样本预测模型，模型精度可由均方根误差（RMSE）、平均绝对误差（MAE）、决定系数R2表示，具体公式为：

2 实例分析

基于Matlab2018a 软件，将20 个样本的实测数据输入模型中，将1～15 个样本数据用于训练模型，16～20 号样本预测模型，不同模型预测结果可见表1。由表中可以看出，不同模型模拟的精度不同，其中，CSA-ANN 模型的精度最高，其与实测值的相对误差在0.1%～1.7%之间，传统的ANN 模型计算结果与实测值的相对误差在9.9%以上。

表1 不同模型承载力模拟值

为进一步比较不同模型的精度，在表2 中计算了不同模型的模拟精度指标。由表中可以看出，CSA-ANN 模型的精度最高，其误差指标最低，决定系数R2达到了0.990，PSO-ANN 模型和GA-ANN 模型的精度次之，ANN 模型的精度最低。

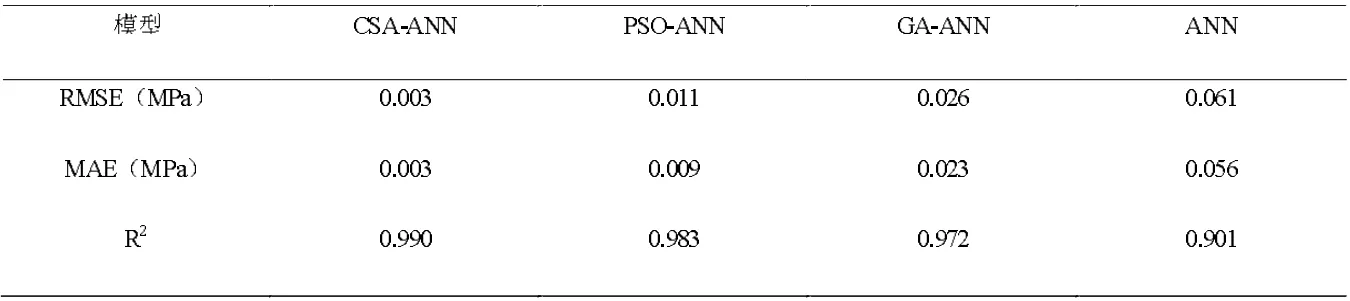
表2 不同模型计算结果精度指标对比

为进一步得出影响水利工程复合地基承载力的关键影响因素，本研究采用了不同数据输入组合方式，比较了不同参数输入下的CSA-ANN 模型精度。参数输入组合方式可见表3。表4 中列出了不同参数组合下的模型精度。由表中可以看出，在全输入组合下的CSA-ANN 模型精度最高。当输入参数个数为3 时，CSA-ANN2 模型精度最高，CSA-ANN4 模型精度次之，这表明影响复合地基承载力的因素由高到低为置换率、施工工艺、孔隙比。而当输入参数个数仅为2时，CSA-ANN6 模型在所有模型中精度最低，但精度与CSA-ANN 模型相差不大，这表明桩长、桩径与复合地基承载力的相关性较高。